On Decomposition of the ABS Lattice Equations and Related Bäcklund Transformations
- DOI
- 10.1080/14029251.2018.1440741How to use a DOI?
- Keywords
- ABS list; decomposition; Bäcklund transformation; solutions; weak Lax pair
- Abstract
The Adler-Bobenko-Suris (ABS) list contains scalar quadrilateral equations which are consistent around the cube, and have D4 symmetry and tetrahedron property. Each equation in the ABS list admits a beautiful decomposition. We revisit these decomposition formulas and by means of them we construct Bäcklund transformations (BTs). BTs are used to construct lattice equations, their new solutions and weak Lax pairs.
- Copyright
- © 2018 The Authors. Published by Atlantis Press and Taylor & Francis
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. Introduction
It is well known that discrete integrable systems play important roles in variety of areas such as statistic physics, discrete differential geometry and discrete Painlevé theory. Quadrilateral equations are partial difference equations defined on four points (see Fig. 1(a)), with a form
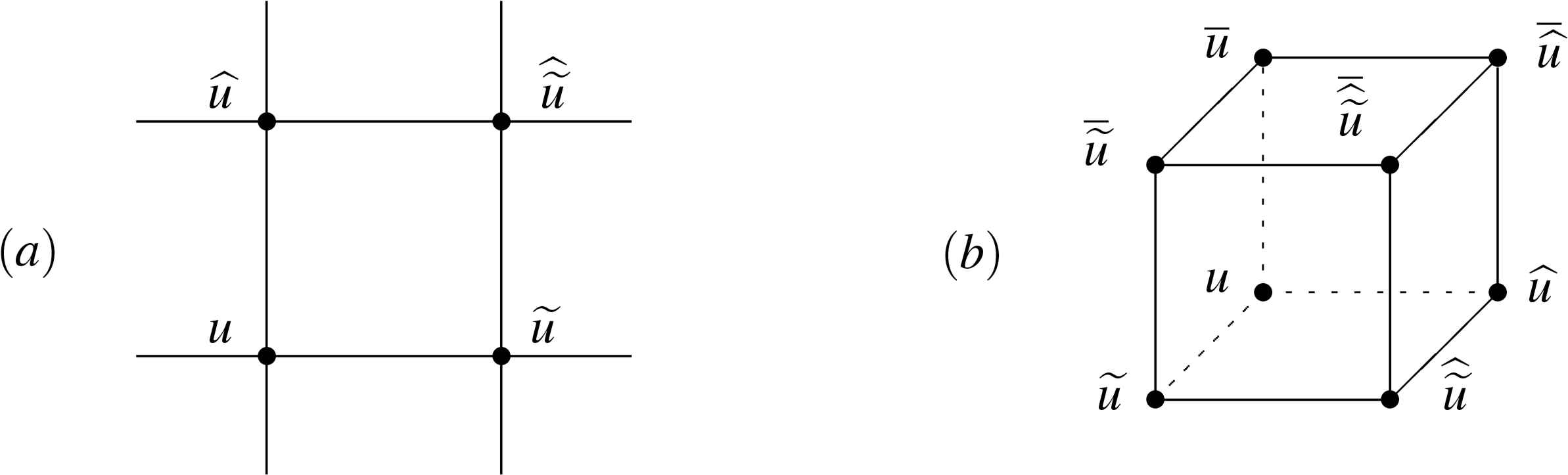
(a). An elementary quadrilateral. (b). The consistency cube.
If the top equation in the consistency cube is viewed as same as the bottom equation but with
BT originated from the construction of pseudo-spherical surfaces and BTs have been playing important roles in soliton theory [15,22,23]. In this paper, we will consider the ABS list and focus on those BTs that can be constructed by using decomposition property of the ABS equations. In fact, each equation Q = 0 in the ABS list admits a decomposition which is an analogue of the following,
The paper is organized as follows. In Sec. 2 we revisit decomposition of the ABS list. In Sec. 3 we discuss possible forms of h and the related quadrilateral equations of u and U, which are listed in Table 1 and 2. Sec. 4 includes some examples as applications, a new weak Lax pair of Q1(0), new polynomial solutions of Q1(δ) and rational solutions of H3*(δ) in Casoratian form are obtained. Finally, Sec. 5 is for conclusions.
| No. | BT(3.1) | u-equation | U-equation |
|---|---|---|---|
| 1 |
|
Q1(0, p2, q2) | lpmKdV |
| 2 |
|
H2 | H1(2p;2q) |
| 3 |
|
A1(δ, p2, q2) | H3(δ;2p;2q) |
| 4 |
|
H3(δ) | H3(− δ) |
| 5 |
|
(A.11) | H3(1) with U → U− 1 |
| 6 |
|
A2 |
|
Consistent triplets.
| No. | BT(3.1) | u-equation | U-equation |
|---|---|---|---|
| 1 |
|
Q1(δ) |
|
| 2 |
|
A1(δ) |
|
| 3 |
|
A2 |
|
| 4 |
|
H3(δ) |
|
| 5 |
|
A2 | A2 |
| 6 |
|
A2 |
|
BT(3.1) related to Q1(δ), A1(δ), H3(δ) and A2.
2. Decomposition (1.5) of the ABS list
2.1. Decomposition (1.5): revisited
Let us revisit the decomposition (1.5) and have a look at the relation of Q and P from a general viewpoint. Consider
In the following let us take a close look at the relation between Q and P in (1.5). Similar to (1.6) we define
Proposition 2.1.
For the polynomial Q given in (2.1), P defined in (1.5) and hij in (1.6), there is a constant K such that
In particular when K = 0, P can be factorized as a product of distinct linear function ai ui + bi.
Proof. It has been proved that
Corresponding to the structure in (1.5), there must be
Since
If K = 0, then we have gij = 0 in light of (2.3). Noticing that
The above proposition reveals an “adjoint” relation between Q and P if Q is an affine-linear quadrilateral polynomial (2.1). For A-type and Q-type ABS equations, one can see that Q and P are almost same.
2.2. Decomposition of the ABS list
For each equation (1.1) in the ABS list it holds that [1]
We note that for the ABS equations, the case K = 0 in Proposition 2.1 corresponds to H-type equations in the ABS list; for H-type equations P is a constant and for H1 even P = 0; for A-type and Q-type equations, Q and P differ only in the parameter q.
3. Bäcklund transformations
In Section 1 by H3(δ) as an example we have illustrated its decomposition can be used to construct a BT. Motivated by the decomposition (2.5) of the ABS equations, we consider the following system
As for generating solutions, we note that for H2 and H3, u solved from (3.1) with corresponding h’s will provide a solution to these two equations, while for the rest equations in the ABS list there is uncertainty. For example, for Q1, we do not know whether u solves Q1 or
3.1. Consistent triplets
When h is defined as (3.4), for the relation of h and possible forms of u-equation and U -equation, we have the following.
Theorem 3.1.
When h(u,
Proof. When h(u,
From the consistency
When s3 = 0, (3.4) turns to be (3.5). In this case, the system (3.1) is a BT for u -equation
Here we note that equation (3.8), (3.9) and the BT (3.1) compose a consistent triplet (cf.[24]), i.e. viewing the BT(3.1) as a two-component system, then the compatibility of each component yields a lattice equation of the other component which is in the triplet.
When function s3 ≠ 0, we have
Note that replacing s0 with
Now we have obtained four quadrilateral equations, (3.8), (3.9), (3.10) and (3.11), all of which are derived as a compatibility of (3.1). Among them, equation (3.8) with s0 = 1, s1(p) = p − a, s2(p) = p + a can be considered as the Nijhoff-Quispel-Capel (NQC) equation with b = a(cf. [19] and eq. (9.49) in [10]).
3.2. CAC property with h given in (3.5) and (3.6)
Although (3.8), (3.9), (3.10) and (3.11) are derived as a compatibility of (3.1), it is not true that they are CAC for arbitrary si. After a case-by-case investigation of the CAC property of the four equations, we reach a full list that includes all CAC equations when h are given in (3.5) and (3.6) which is presented in the following theorem:
Theorem 3.2.
For the system (3.1) where h is affine-linear as given in (3.5) and (3.6), if it generates a consistent triplet and acts as a BT between quadrilateral equations which are CAC, the exhausted results are
Proof of the theorem is given in Appendix A.
Here we have two remarks. First, most of the BTs in Table 1 can be found from known literatures. For example, transformation 1 was already known in [16,18,20] as a BT connecting the lattice Schwarzian KdV (Q1(0)) equation and lpmKdV equation, transformation 2 and 3 were given in [3], transformation 6 can be found from eq. (57) of [6] by first taking (A, B, C) = (1,0,0), then (0,0,1) and next eliminating s, t from the obtained equations, transformation 4 can be found from eq. (58) of [6] by first taking (A, B, C) = (0,1,0), then (0,0,1) and next eliminating s, t from the obtained equations. The second remark is although transformation 1 is a special case of 3 by taking δ = 0 and imposing a point transformation, we would like to keep it in the table because it does not only connect the lattice Schwarzian KdV equation and lpmKdV equation but also plays a practical role in deriving lattice equations in Cauchy matrix approach [17] as well as in generating rational solutions [24].
3.3. Other cases: Q1(δ), A1(δ) and A2
For equations Q1(δ), A1(δ) and A2, their h polynomials are not affine linear. We discuss them one by one.
First, for Q1(δ), the corresponding system (3.1) is
Similarly, for A1, we find
For A2, in the system (3.1) there is
It is hard to write out a U -equation in a neat form. However, by observing that U is arbitrary in (3.1), we can replace U with U / f(u) where f(u) is a suitable function of u so that the deformed BT
We collect the BTs obtained in this subsection in Table 2.
In this section we have given an exhausted examination for the case where h is the affine-linear polynomial (3.4). For Q1(δ), A1(δ) and A2, their h polynomials are not affine linear and their corresponding U -equations are usually multi-quadratic counterparts of the ABS equations, (see Table 2). For Q2, Q3 and Q4, their h polynomials are so complicated that from system (3.1) we can not derive explicit U -equations.
We also note that there are many systematical works to consider constructions of BTs for quadrilateral equations [3,6,13,14]. In [6] many BTs are constructed by considering compatibility of (3.3) which are Riccati equations in terms of U but allowing more freedom for u. Besides, [6] presents variety of BTs with free parameters (A, B, C) that are derived by using Yang-Baxter maps. BTs in Table 2 are included in the results of [6].
4. Applications
BTs have been used as a main tool to find rational solutions for quadrilateral equations (see [24]). In this section we would like to introduce more applications, including a BT and weak Lax pair of Q1(0), polynomial solutions of Q1(δ) and rational solutions of H3*(δ).
4.1. BT and weak Lax pair of Q1(0)
From the previous discussion, we know that Q1(0),
The BT (4.3) yields a pair of linear problems (Lax pair):
In addition to the weak Lax pair of Q1(0), we have shown an approach to construct auto-BT for u -equation from (3.1) if U -equation admits a symmetry U → 1 / U. For A2 and related BT (3.21), employing the same technique, we have relations
Both of them are auto BTs of A2.
4.2. Polynomial solutions of Q1(δ)
Consider (3.12), i.e.
In other words, (4.8) may also be a BT between
To solve (4.8) which is a quadratic system, we suppose that U is a polynomial of
Theorem 4.1.
When U is given in (4.11), we can convert the system (4.8) to
When N ≥ 1 and we require that vi have the following form,
The proof for this theorem is given in Appendix B.
Let us turn to find polynimial solutions. When N = 0, we have U = c0 and
Suppose
It turns out that four possibilities for u are
When N = 1,2, with p, q parameterized as
We can check that u and U respectively satisfy Q1(δ) and H3*(δ) equation (3.13). These are polynomial solutions.
4.3. Rational solutions of H3*(δ)
One can derive rational solutions for H3*(δ) from those of Q1(δ) and BT (3.12).
It has been proved that Q1(δ) with p, q parameterized as in (4.17) has the following rational solutions [24]:
The Casoratian f defined above satisfies a superposition relation [24]
Making use of (3.12), (4.19), (4.20) and (4.21), by a direct calculation we find rational solutions of H3*(δ) (3.13) can be written as
The first three solutions are
Here U2 is (4.18b) with c0 = 1
Finally, we note that, compared with the solution of H3(δ) given by [24], which is
5. Conclusions
BTs contain compatibility and are closely related to integrability of the equations that they connect. In this paper we have investigated system (3.1) as a BT. When h is affine linear with a generic form (3.4), we made a complete examination and all consistent triplets are listed in Table 1. As applications, apart from constructing solutions (cf. [24]), these BTs in the triplets can be viewed as Lax pairs of u -equations, where wave function Φ = (g, f)T can be introduced by taking U = g / f but usually it is hard to introduce an significant spectral parameter. When h is beyond affine linear, system (3.1) as a BT and the connecting quadrilateral equations (including multi-quadratic ones) are listed in Table 2. Further applications of the obtained BTs, such as constructing weak Lax pair and rational solutions for multi-quadratic lattice equations, were also shown in the paper.
Acknowledgments
We are grateful to the referees and editor for their invaluable comments. This project is supported by the NSF of China (Nos. 11371241,11631007 and 11601312).
Appendix A. Proof of Theorem 3.2
A.1. Multidimensional consistency: h given in (3.5)
The following discussion is on the basis of the CAC condition
A.1.1. s0 = 0
In this case, it can be verified that (3.8) always satisfies the CAC condition
Without any loss of generality, by assumption of
A.1.2. s0 ≠ 0
A. s1(p) + s2(p) = ks0(p) with constant k
This goes to the case of s0 = 0 by taking u → u−k− 1 when k ≠ 0 and u → u−s0(p)n − s0(q)m when k = 0.
B. s1(p) + s2(p) = ks0(p) with nonconstant k
Check all terms in
Letting (A.2) vanish leads to only three subcases.
Case B.1. A = 0
It directly results in
Then from the coefficient of
If E = 0, it returns to the Case A. In fact, when E = 0, under (A.3) we have
In the case that F = 0 and s1(p) is not a constant, it again returns to Case A. In fact, in this case from F = 0 we can take s0 to be the form
Case B.2. A ≠ 0, B = C = 0
B = 0 yields either s2(r) + s1(r) = 0 or s0(p)s1(p) = c0 with constant c0. The former belongs to Case A and then we consider the later, i.e.
Note that if the term
Making use of (A.5) and (A.6) we reach
We ignore solution s0 = c because this leads to s1 and s2 to be constants and then brings the case to Case A. Therefore we have c1 = ±c0. Since c1 = −c0 results in k = 0 which is Case A, the only choice is c1 = c0 and in this case the canonical form for h can be
Then it follows that (3.8) is A1(δ; p2, q2), and the corresponding (3.9) is H3(δ; 2p, 2q).
Case B.3. A B ≠ 0, B + C = 0
Since B ≠ 0, from B + C = 0 we can assume
Note that in Case B s0(r) and
We note that (A.9) is already discussed in [3]. After making u → u−1 / c1 in (A.9) we can consider
A.2. CAC property: h given in (3.6)
For
If s3(p) is a constant, setting s3(p) = 1, s0(p) = pδ, we have
If s0(p) is a constant, by setting s0(p) = 1, s3(p) = pδ, it comes out that
If neither s0(p) or s3(p) is a constant, ∂p∂q(A.10) yields
We note that (A.11) is not a new equation. It is related to Q1(0; p2, q2) by
As a conclusion we have proved Theorem 3.2.
Appendix B. Proof of Theorem 4.1
According to the BT (4.8) and assumption (4.11) and (4.12), we can assume that vi have the following special form
Lemma B.1.
With U defined in (4.11) and v1, v2 defined above, when N ≥ 1, we have
Proof. Substituting (4.11) and (B.1) into system (4.8) and (4.13), from the coefficient of the leading term x2N (if N ≥ 1) in (4.8) we find
Consequently we have
Since p, q are independent constants, it follows that θ1 = θ1(n), θ2 = θ2(m). Consequently, from the coefficient of xN−1(N ≥ 1) in (4.13) we have
Lemma B.2.
With U defined in (4.11) and v1, v2 defined in (B.2), when N ≥ 1, the allowed values of N are only 1,2.
Proof. Analyzing the coefficient of xN − 1(N ≥ 1) in (4.13), we obtain f0b = g0a, which leads to
Substituting (B.2), (4.17) and (B.4) into the coefficient of x2N − 1(N ≥ 1) in (4.8), we can work out
Then substituting (4.17)– (B.5) into the coefficient of xN − 2(N ≥ 2) in (4.13), we find it varnishes. Next, analyzing the coefficient of x2N − 2(N ≥ 2) in (4.8), we have
Substituting (4.17)–(B.6) into the coefficient of xN − 3(N ≥ 3) in (4.13), we obtain
Footnotes
By this we denote Q1(0) in which replacing p and q by p2 and q2
References
Cite this article
TY - JOUR AU - Danda Zhang AU - Da-jun Zhang PY - 2021 DA - 2021/01/06 TI - On Decomposition of the ABS Lattice Equations and Related Bäcklund Transformations JO - Journal of Nonlinear Mathematical Physics SP - 34 EP - 53 VL - 25 IS - 1 SN - 1776-0852 UR - https://doi.org/10.1080/14029251.2018.1440741 DO - 10.1080/14029251.2018.1440741 ID - Zhang2021 ER -
