Nonlocal symmetries and group invariant solutions for the coupled variable-coefficient Newell-Whitehead system
- DOI
- 10.1080/14029251.2020.1819601How to use a DOI?
- Keywords
- Nonlocal symmetry; Group invariant solution; Lie point symmetry; Symmetry reduction; Variable-coefficient Newell-Whitehead system
- Abstract
Starting from the Lax pairs, the nonlocal symmetries of the coupled variable-coefficient Newell-Whitehead system are obtained. By introducing an appropriate auxiliary dependent variable, the nonlocal symmetries are localized to Lie point symmetries and the coupled variable-coefficient Newell-Whitehead system is extended to an enlarged system with the auxiliary variable. Then the finite symmetry transformation for the prolonged system is found by solving the initial-value problems. Furthermore, by applying symmetry reduction method to the enlarged system, two kinds of the group invariant solutions are given.
- Copyright
- © 2020 The Authors. Published by Atlantis Press and Taylor & Francis
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. Introduction
Symmetry study is always a powerful method in physics and mathematics fields [1] . Especially in soliton theory, the study of symmetries is more important because of the following three important applications. The first is using symmetry to obtain new solutions from old ones [2–7 ]. The second is symmetry can be used to reduce dimensions of a partial differential equation(PDE) [8, 9]. The third one is that any flow equation corresponding to a symmetry of integrable models is an integrable one, that is to say, through symmetry a new soliton equation can be acquired [10–12 ]. For these reasons, there are many other interesting applications of the symmetry study [13–17 ]. Nonlocal symmetry as a generalization of the symmetry was first researched by Vinogradov and Krasil’shchik in 1980, which enlarges the class of symmetries and connected with integrable models. Compared with the local symmetry, the nonlocal symmetries of PDE are not easy to find and its similarity reductions cannot be calculated directly. However, the importance of the nonlocal symmetry has attracted many mathematicians to make great efforts to explore it and achieve fruitful results, such as in reference [4] , Galas presented the nonlocal Lie-Bäcklund symmetries by using the Pseudo-potentials, in [8], [18–20], Bluman, Euler et al. constructed nonlocal symmetries of PDES by using potential system, Lou, Hu and Chen derived the nonlocal symmetries from the Bäcklund transformation [21] . Recently, based on the auxiliary system (lax pair), Xin and Chen obtained the nonlocal symmetries for the modified Korteweg-de Vries equation [23] , Miao, Xin and Chen obtained the nonlocal symmetries for the Ablowitz-Kaup-Newell-Segur system [24] . Gao, Lou and Tang found that Painlevé analysis can be applied to obtain nonlocal symmetries corresponding to the residues with respect to the singular manifold of the truncated Painlevé expansion, which is also called residual symmetries [25] . Besides, considering the results obtained from nonlocal symmetry reduction, many references [26–32] have shown that nonlocal symmetry method is one of the effective tools to find nonlinear waves interacting with each other.
In this paper, further generalizing the method based on lax pair to construct nonlocal symmetries for the variables coefficient system, and then employing this method to the coupled variable-coefficient Newell-Whitehead system, we achieve the nonlocal symmetries of system (2.1), and use the obtained nonlocal symmetries to construct group invariant solution for it. Because of the variables coefficient equation contain the corresponding constant coefficient equation, this study is very meaningful.
This paper is arranged as follows: in Section 2, nonlocal symmetries of coupled variable-coefficient Newell-Whitehead system are obtained by using the Lax pair. In Section 3, by extending the original system, nonlocal symmetries are transformed into the Lie point symmetry, and the corresponding finite transformation group are given with Lie’s first theorem. In Section 4, some symmetry reductions and group invariant solutions of system (2.1) are obtained with lie point symmetry of prolonged system. A short conclusion and discussion is included in the last Section.
2. Nonlocal symmetries of the coupled variable-coefficient Newell-Whitehead system
The coupled Newell-Whitehead system is given by
The system (2.1) can efficiently describe many nonlinear phenomena which appear in fluid mechanics, plasma physics, thermonuclear reactions, and population proliferation. The literature [33] has studied the Darboux transformation and multi-soliton solutions for system (2.1), so our main objective in this paper is to obtain nonlocal symmetries for the coupled variable-coefficient Newell-Whitehead system from its Lax pair, and further to localize the nonlocal symmetries by introducing potential variables, then by the method of symmetry reduction to derive the interaction solution of system (2.1). To the best of our knowledge, the nonlocal symmetries and interaction solution to the system (2.1) have not been discussed.
The lax pair of system (2.1) reads [33]
For system (2.1), we consider the invariant property under
3. Localization of the nonlocal symmetry
We know that Lie point symmetry can be applied to construct explicit solutions for PDEs, however, it is invalid for nonlocal symmetry. So we need to transform the nonlocal symmetries into local ones, especially into Lie point symmetries. Following this idea, we extend the original system to a closed prolonged system by introducing some auxiliary variables, and construct the Lie point symmetries for the prolonged system which contains the nonlocal symmetries (2.6) of the original system.
For simplicity, letting
To localize the nonlocal symmetries (3.1), we have to solve the following linearized equations
It is easy to verify that the solutions of (3.2) have the following forms
Remark 3.1.
What is more interesting here is that the symmetry σ f shown in (3.6) indicates that the auxiliary-dependent variable f satisfying
From the expression (3.4), one can see that the nonlocal symmetries (3.1) in the original space x, t, p, q, α, β have been successfully localized to a lie point symmetries
To proceed, we study the finite symmetry transformation of the Lie point symmetry (3.9). According to Lie’s first theorem, solving the following initial value problem:
Theorem 3.1.
If {p, q, α, β, ϕ1, ϕ2, f } is a solution to the prolonged system (2.1), (2.2) and (3.5), then so is the {
Remark 3.2.
From the Theorem 3.1. one can see that the finite symmetry transformation (3.11) can give a new solution
Next, we study the Lie point symmetries of the prolonged system instead of the single Eq. (2.1). According to the classical Lie point symmetry method, we assume that the vector of the symmetries has the following form
Substituting Eq. (3.13) into (2.4), (3.2) and (3.14), eliminating the pt, qt, ϕ1x, ϕ1t, ϕ2x, ϕ2t, fx, ft, and collecting the coefficients of the independent partial derivatives of dependent variables p, q, α, β, we obtain a system of overdetermined linear equations for the infinitesimals X, T, P, Q, A, B, P1, P2, F, and by solving these determining equations, we can obtain the following results
4. Symmetry reduction and group invariant solutions to the coupled variable-coefficient Newell-Whitehead system
In order to derive the group invariant solutions in this Section, we solve the symmetry constraint conditions σi = 0 (i = 1,...,7) defined by (3.13) with (3.15), which is equivalent to solving the following characteristic equation:
Solving the characteristic equation (4.1) under the condition of c2 ≠ 0, we obtain two nontrivial similar reductions and several substantial invariant solutions listed in the follows.
Case 1: c4 ≠ 0
Without the loss of generality, we assume c1 = 1, c2 = 1, c3 = 0, c4 = k1, F4(t) = k2, F5(t) = k3, with k1, k2, k3 are arbitrary constants, so the similarity solutions can be obtained after solving out the characteristic equations (4.1)
It is easy to verify that the equation (4.4) is equivalent to the following elliptic equation
It is obvious that once the F1 is solved with Eq. (4.4), F2, F3, F4, F5 can be obtained directly from Eq. (4.3). From Eq. (4.5), we know that F can be written in terms of Jacobi Elliptic functions, with F bearing the following form
Substituting Eq. (4.7) into Eq. (4.5) and solving the over-determined equations with Maple will yield
In Fig. 1, we plot the interaction solutions between solitary waves and elliptic function waves expressed by (4.2) with parameters {k1 = 1, k2 = 10000, b1 = 1000, k3 = 10, C1 = 0.10, C2 = 0.1, λ = 0.001}.
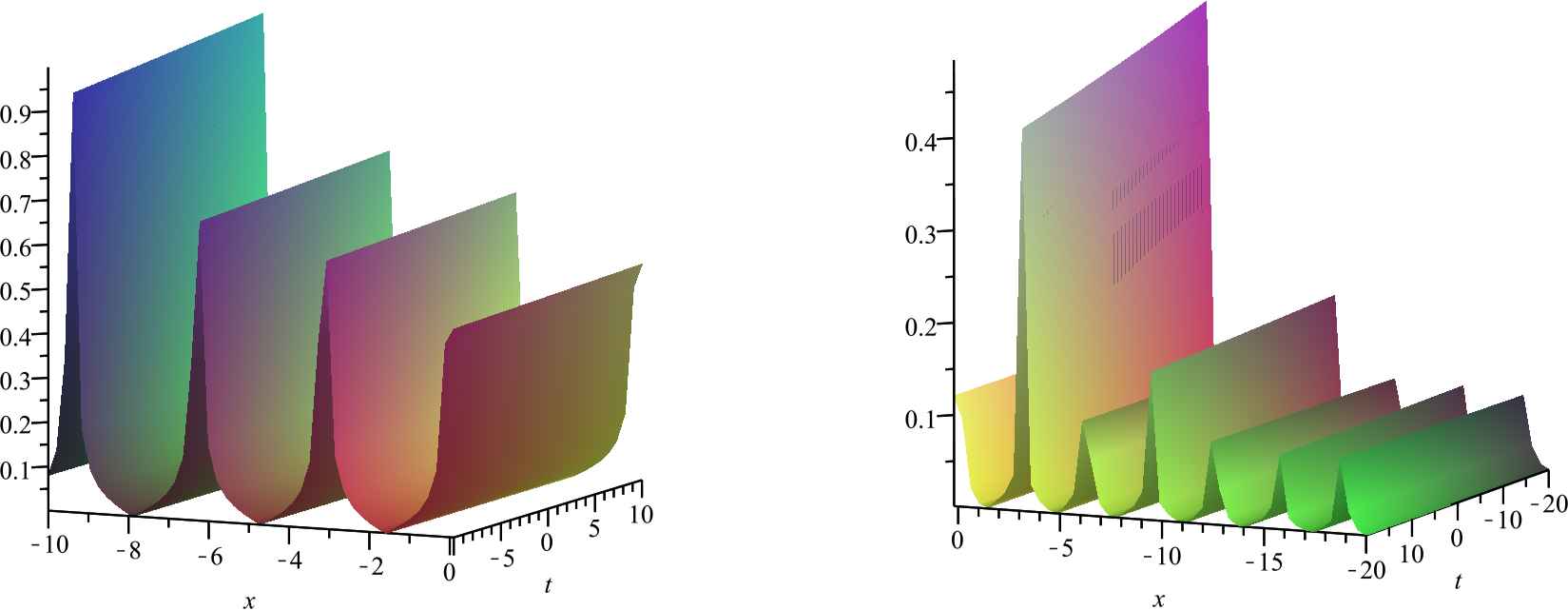
The 3-D soliton-cnodial periodic wave interaction solutions to p and q of the variable coefficient Newell-Whitehead system.
Case 2: c4 = 0
Assume c1 = k4, c2 = k5, c3 = 0, c4 = 0, F1(t) = 1, F4(t) = 1, with k4, k5 as arbitrary constants. Solving the following characteristic equations
Substituting Eq. (4.10) into the prolonged system yields
Then, another type of soliton-cnodial wave solutions can be obtained via taking
Substituting the expressions (4.15), (4.14) and (4.11) into (4.10) comes the exact solutions for the variable coefficient Newell-Whitehead system (2.1), which proves that the solutions p, q are rational functions.
5. Summary and Discussion
On the basis of the classical Lie point method and Lax pair, by making some changes of the assumption of the symmetry, we not only derive the local symmetries, but also the nonlocal ones to the variable coefficient Newell-Whitehead system. The latter is the prime object of this paper. By introducing the auxiliary variable, the nonlocal symmetries are readily localized to Lie point symmetry via extending the original system to a large system. Meanwhile, in the process of localization, the corresponding Schwartz form of the system (2.1) is given from the Lax pair. Then exploring the Lie group theorem to these local symmetries, the group invariant solutions of system (2.1) are derived. Moreover, by using standard Lie point symmetry approach to study the similarity reductions of the prolonged system, two types of group invariant solution are presented in this paper, including the special interaction solution between the soliton and the cnodial periodic wave, and the soliton with rational function solution. This kind of solution can be easily applicable to the analysis of physically interesting processes.
The method presented in this paper could be applied to other variable coefficient integrable models. One can also consider another interesting subject, the relationship between nonlocal symmetry obtained from the Lax pair and other methods, such as the truncated Painlevé expansion and Darboux transformation method. Furthermore, though the localization is the important step to expand application of the nonlocal symmetry, there is no universal way to estimate which type of nonlocal symmetry can be localized to the point symmetry, which will be discussed in our future work.
Acknowledgments
The project is supported by the National Natural Science Foundation of China (Grant Nos. 11471004, 11775047, 11505090), The Chinese Post doctoral Science Foundation (No. 2020M673332), the Natural Science Foundation of Shaanxi Province (No. 2018JQ-1045), Research Award Foundation for Outstanding Young Scientists of Shandong Province (No. BS2015SF009) and the Science and Technology Innovation Foundation of Xi’an (2017CGWL06), the Scientific research project of Shaanxi Provincial Department of Education (No. 19JK0737).
References
Cite this article
TY - JOUR AU - Yarong Xia AU - Ruoxia Yao AU - Xiangpeng Xin PY - 2020 DA - 2020/09/04 TI - Nonlocal symmetries and group invariant solutions for the coupled variable-coefficient Newell-Whitehead system JO - Journal of Nonlinear Mathematical Physics SP - 581 EP - 591 VL - 27 IS - 4 SN - 1776-0852 UR - https://doi.org/10.1080/14029251.2020.1819601 DO - 10.1080/14029251.2020.1819601 ID - Xia2020 ER -
