Minimal surfaces associated with orthogonal polynomials
- DOI
- 10.1080/14029251.2020.1819599How to use a DOI?
- Keywords
- Integrable system; soliton surface; minimal surface; orthogonal polynomial; Weierstrass immersion formula; Sym-Tafel immersion formula; CMC surface
- Abstract
This paper is devoted to a study of the connection between the immersion functions of two-dimensional surfaces in Euclidean or hyperbolic spaces and classical orthogonal polynomials. After a brief description of the soliton surfaces approach defined by the Enneper-Weierstrass formula for immersion and the solutions of the Gauss-Weingarten equations for moving frames, we derive the three-dimensional numerical representation for these polynomials. We illustrate the theoretical results for several examples, including the Bessel, Legendre, Laguerre, Chebyshev and Jacobi functions. In each case, we generate a numerical representation of the surface using the Mathematica symbolic software.
- Copyright
- © 2020 The Authors. Published by Atlantis Press and Taylor & Francis
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. Introduction
To describe the behavior of a continuous medium (fluid, gas or solid), theoretical physics uses various models, most of which lead to nonlinear partial differential equations (PDEs). The study of the general properties of these nonlinear equations and of the methods for solving them is a rapidly developing area of modern mathematics. Specifically, this is true in the study of integrable models in two independent variables, which have generated a great deal of interest and activity in several mathematical as well as physical fields of research. In particular, surfaces immersed in Lie groups, Lie algebras and homogeneous spaces which are associated with these models have been shown to play an essential role in several applications to nonlinear phenomena in diverse areas of physics, chemistry and biology (see e.g. [1–10] and references therein). An algebraic approach to the structural equations of these surfaces (i.e. the Gauss-Weingarten (GW) and Gauss-Codazzi (GC) equations) has often been very difficult to carry out. A geometrical approach to the derivation and classification of such systems, which we propose here for special functions, seems to be of importance for applications in several branches of science. The construction and investigation of two-dimensional (2D) surfaces obtained through the use of the soliton surface technique [11] allows the plotting of these functions, which constitutes the main objective of this work. We examine certain aspects of a visual image of surfaces reflecting the behavior of some special functions, focusing mainly on such functions as the Bessel, Legendre, Laguerre, Chebyshev and Jacobi functions and the associated series [12–16], which can be of interest. This may provide some clues about the properties of these surfaces, which are otherwise hidden in some implicit mathematical expressions. This is, in short, the main topic of investigation.
The paper is organized as follows. Section 2 contains a brief summary of the results concerning the construction of minimal and constant mean curvature lambda (CMC-λ) surfaces (H = λ) immersed in the three-dimensional (3D) Euclidean and hyperbolic spaces, respectively. It is shown that the use of successive gauge transformations allows us to reduce the GW system of equations for the moving frame on these surfaces to a single linear second-order ordinary differential equation (ODE). The coefficients of this ODE are expressed in terms of two arbitrary holomorphic functions. Comparing them with the coefficients of the ODE associated with orthogonal polynomials allows us to construct their associated 2D-surfaces. It is shown that these surfaces are defined by the Weierstrass formula for immersion. The properties of surfaces associated with these polynomials are discussed in detail. In section 3, we illustrate the theoretical considerations for several classical orthogonal polynomials. We summarize the obtained results in tables 1 to 8. This analysis includes explicit solutions of the GW system, that is the wavefunctions and their potential matrices. For each orthogonal polynomial, a 3D numerical representation is constructed and investigated. The last section contains remarks and suggestions regarding possible further developements.
| The Legendre equation: |
Note: Pα, Qα : αth-order Legendre polynomials, 1st and 2nd kind.
Δ1 = α(α + 1), Δ2 = α(α + 2),
Summary. The Legendre equation
| The Legendre associated equation: |
Note:
Δ = α(α + 1), ϕ1 = log(1 + z), ϕ2 = log(1 − z).
Summary. The Legendre associated equation
| The Bessel equation: |
Note: 𝒥p, 𝒴p: p
th-order Bessel functions, 1st and 2nd kind.
Summary. The Bessel equation
| The Chebyshev equation of the 1st kinda: |
Note: Tn, T2,n: Chebyshev polynomials, 1st and 2nd kind. ϕ = arcsin(z).
To obtain the results for the Chebyshev equation of the 2nd kind, we perform the transformation
Summary. The Chebyshev equations
| The Laguerre associated equation: |
Note: Γ(ν, z): Incomplete gamma function,
Summary. The Laguerre associated equation
| The Hermite equation: |
Note: Hn: nth-order Hermite polynomial, pFq: Hypergeometric function.
Summary. The Hermite equation
| The Gegenbauer equation: |
Note: pFq: Hypergeometric function.
Summary. The Gegenbauer equation
| The Jacobi eq.: |
Note: pFq: Hypergeometric function. DomainJacobi = {ξ ∈ ℂ | |ξ| < 1 and |ξ + 1| < 2|α|}.
Δ = 2α n(n + α + β + 1),
Summary. The Jacobi equation
2. Linear problem and immersion formulas
In this section, according to [17] , we recall the main concepts required to study the linear problem (LP) related to the GW equations for frames on 2D-surfaces, which are the Enneper-Weierstrass and Sym-Tafel formulas for immersion, both in Euclidean and hyperbolic spaces. We make use of the gauge transformations in order to reduce the LP to a single linear second-order ODE and to investigate its links with orthogonal polynomials.
2.1. The linear problem for minimal surfaces
To make the paper self-contained, we summarize the basic facts on the immerson of minimal surfaces in the Euclidean space 𝔼3 given in [11,18], together with the quaternionic description of these surfaces in the 𝔰𝔲(2) algebra. Let F be a smooth orientable and simply-connected surface in 𝔼3 given by a vector-valued function
We have used the notation for the holomorphic and antiholomorphic derivatives
The Hopf differential Qdz on ℛ and the mean curvature on F are defined by
The compatibility conditions of the GW equations (2.7), often called the Zero-Curvature Condition (ZCC)
Here 𝒱 = −𝒰† is an anti-Hermitian matrix.
The Enneper-Weierstrass immersion formula for minimal surfaces is defined by the contour integral [19, 20]
We obtain
Note that Ψ is a holomorphic function and 𝒰 is parametrized by λ ∈ ℂ\{0}. The wavefunction Φ in (2.11) can also be expressed in terms of the holomorphic functions η and χ
Let
2.2. Immersion in the hyperbolic space H3(((λ))) of curvature λ
In this section, we use results from the soliton approach [11,22,23] for the study of CMC surfaces in the hyperbolic space H3(λ). Consider the conformal immersion of surfaces in the hyperbolic space
The conformality conditions are given by
The vectors Fσ, ∂Fσ,
We define the functions u, H and Q as in (2.6). The GW equations for the moving frame are given by
In the case of CMC-λ surfaces (H = λ), the reduced GC equations take the form [17]
The reduced linear problem associated with equations (2.26) takes the form
Let us identify the vector X ∈ ℝ3,1 with 2 × 2 Hermitian matrices using the Pauli matrices
The scalar product is then given by
Consider Φ ∈ SL(2, ℂ) which transforms the orthonormal basis B = {𝟙2, σ1, σ2, σ3} into the orthonormal basis (the frame) B′ = {Fσ, ∂xFσ, ∂yFσ, N} by the relation
To study the LP, we define the potential matrices 𝒰, 𝒱 in the 𝔰𝔩(2, ℂ) algebra by
Therefore these matrices take the following explicit form [11]
Note that with the same gauge M (2.14), the gauge transformation process leads to the same structure, either with the transformation of the LP (2.11) associated with minimal surfaces immersed in the Euclidean space 𝔼3, or with the transformation of the LP (2.29) associated with CMC-λ surfaces immersed in the hyperbolic space H3(λ). Therefore, the linear system (2.15) can equivalently be expressed by the system
From a solution Φ of the linear system (2.34), the formula
3. Special functions and associated soliton surfaces
In this section, we examine the ODE (2.36) in the case where it coincides with ODEs describing orthogonal polynomials. We present an example in which we solve the LP associated with the Laguerre polynomial. We discuss the explicit form of the Enneper-Weierstrass representation of 2D-surfaces immersed in 𝔼3 associated with this polynomial. Next, a summary of the results is presented for several classical orthogonal polynomials, under the form of tables, together with 3D images of selected surfaces.
3.1. The Laguerre equation: a complete example
The Laguerre equation for the unknown function ω takes the form
Comparing the coefficients of (3.1) with those of (2.36), we obtain the explicit form of the meromorphic functions η and χ. In general, for an ODE of the form
Making use of (3.6), we eliminate η et χ from equation (2.36) and obtain the Laguerre equation with dependent variable Ψ1
To determine the wavefunction Ψ which satisfies the LP (2.15), we solve (3.8) for its first component Ψ1
The wavefunction Ψ associated with the LP (2.15) takes the form
We simplify the problem to illustrate a particular case of the Laguerre equation and to show a numerical display of the surface in 𝔼3. Let α = 1. The Laguerre equation (3.1) becomes
We verify that 𝒰 and Ψ are solutions of the LP (2.15) using the notation 𝒰Ψ := (Λ1, Λ2)T and verifying that ∂Ψ1 = Λ1, ∂Ψ2 = Λ2.
The Enneper-Weierstrass representation (2.13) takes the form
The quaternionic representation (2.19) of the surface immersed in the 𝔰𝔲(2) algebra takes the form
We keep in mind that the formulas (3.23) and (3.24) describe different representations of the same surface.
The Laguerre equation.
3D numerical display of the Enneper-Weierstrass representation of the surface (3.23) describing the Laguerre equation, obtained by computing ξ0 = 1 + i and ξ = reiθ, r ∈ [−3, 3], θ ∈ [0, 2π].
3.2. Solutions of the linear problem and soliton surfaces associated with orthogonal polynomials
We summarize our results in the form of tables, giving the explicit form of surfaces and LP elements. Each table is made of five parts: the meromorphic functions η (3.4) and χ (3.5), the components of the potential matrix 𝒰 (2.16), the components of the wavefunction Ψ defined by (2.36) and (2.37), the components of the surface F ∈ 𝔼3 (2.13), and the components of the surface
In each case, we consider in the table the parameter λ ∈ ℂ\{0} of the LP (2.15), the parameters {νk : k = 1, 2,...,n} of the specific ODE, and four arbitrary integration constants c1 ∈ ℂ\{0}, c2, k1, k2 ∈ ℂ. To keep the expressions compact, in what follows, we use the notation z* to designate the complex conjugate of z. We identify the special functions appearing in the formulas at the bottom of each table, accompanied by the notations and the constraints, in certain cases. For example, for the Jacobi equation, a restriction on the domain of the parametrization is necessary in order to integrate the functions η and χ, to find the components of the surface and to ensure the convergence of the infinite series. This restriction arises from the chosen representation of the functions appearing in the integrands of the Enneper-Weierstrass formula (2.13)
Each table is accompanied by a numerical 3D representation of a selected surface obtained by fixing the parameters of the classical ODE considered, the parameter of the LP and the integration constants. To keep the expressions in the captions compact, we use the notation

The Legendre equation. 3D numerical display of the Enneper-Weierstrass representation of the surface describing the Legendre equation, obtained by computing
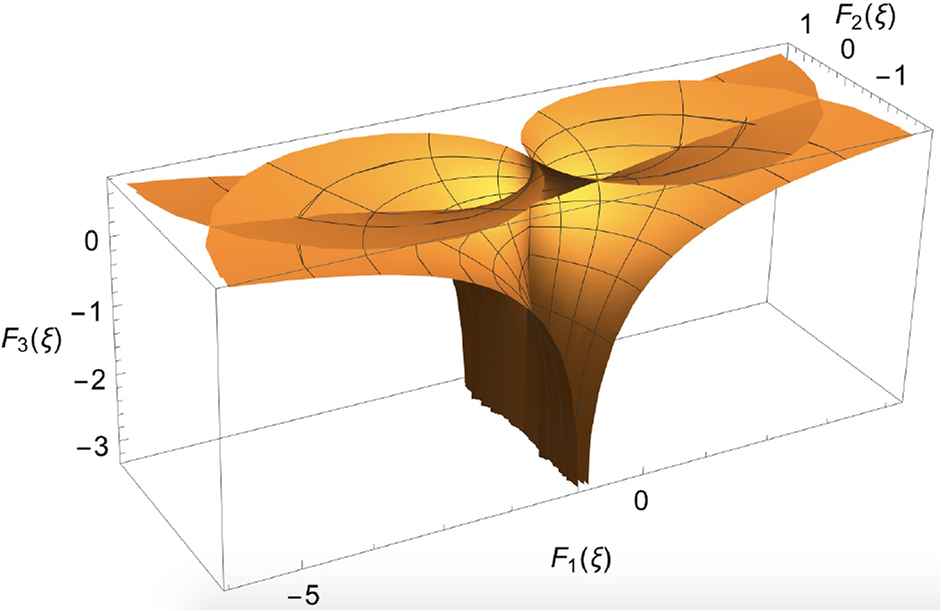
The Legendre associated equation. 3D numerical display of the Enneper-Weierstrass representation of the surface describing the Legendre associated equation, obtained by computing ξ0 = −1 − i, ξ = reiθ, where r ∈ [−5, 5], θ ∈ [0, 2π]. For fixed parameters and constants α = 1, m = 1, c1 = 1, c2 = 0, k1 = 1, k2 = −1,
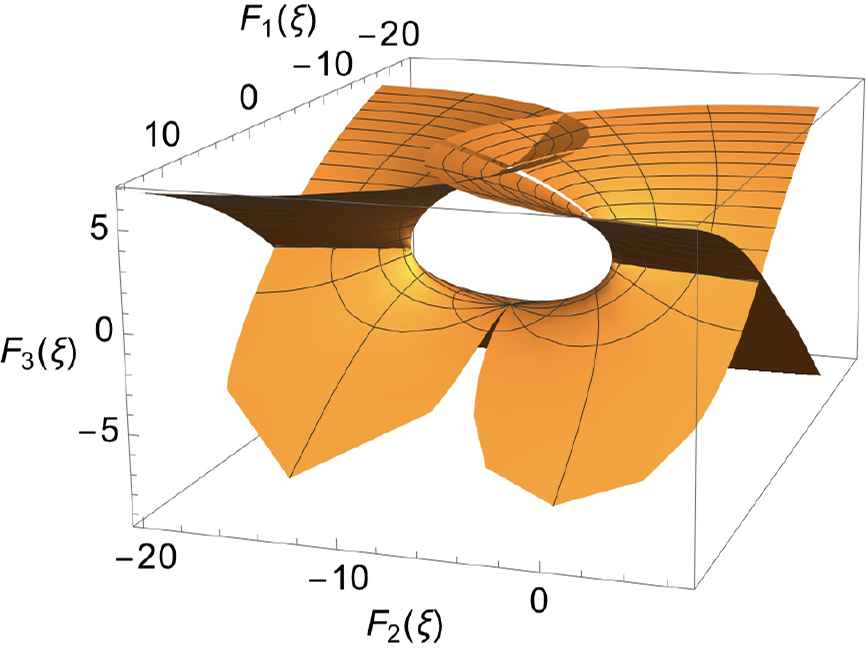
The Bessel equation.
3D numerical display of the Enneper-Weierstrass representation of the surface describing the Bessel equation, obtained by computing ξ0 = 1 and ξ = reiθ, where

The Chebyshev equation. 3D numerical display of the Enneper-Weierstrass representation of the surface describing the Chebyshev equation, obtained by computing ξ0 = 1, ξ = reiθ, where r ∈ [−10, 10], θ ∈ [0, 2π]. For fixed parameters and constants n = 1, c1 = 1, c2 = 0, k1 = 1, k2 = 1, λ = −1, we obtain
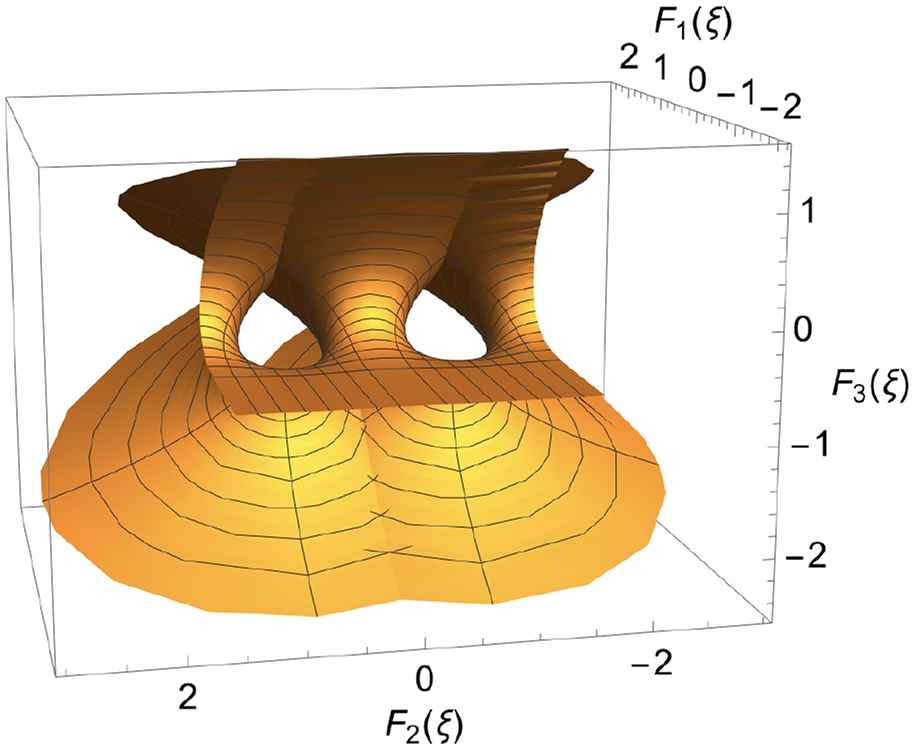
The Laguerre associated equation.
3D numerical display of the Enneper-Weierstrass representation of the surface describing the Laguerre associated equation, obtained by computing ξ0 = 3 + 3i, ξ = x + iy, where x ∈ [−3, 3],
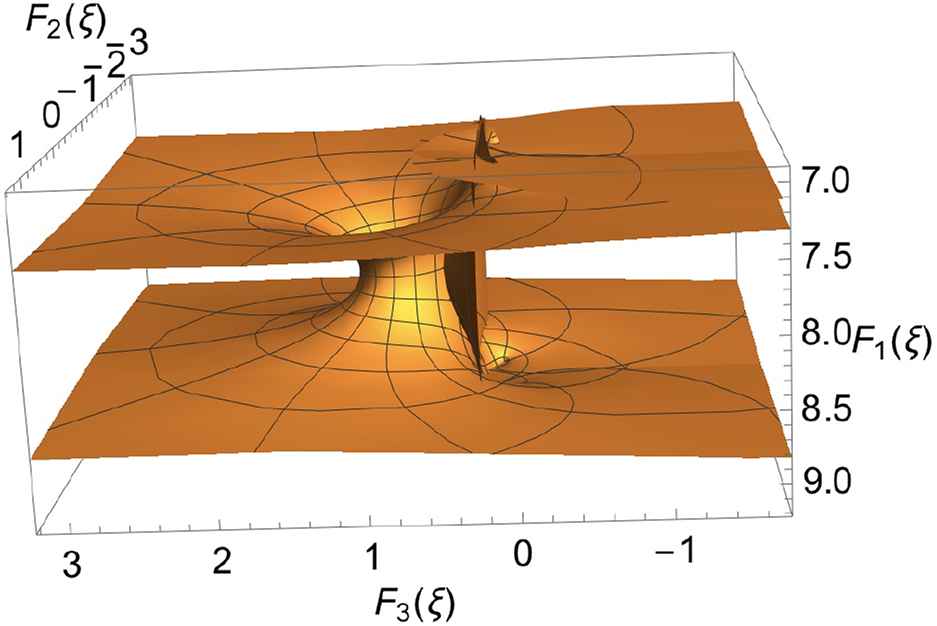
The Hermite equation.
3D numerical display of the Enneper-Weierstrass representation of the surface describing the Hermite equation, obtained by computing ξ0 = 1 + 3i and ξ = x + iy, x ∈ [−2, 2], y ∈ [−2, 2]. For fixed parameters and constants n = 1, c1 = 1, c2 = 0,
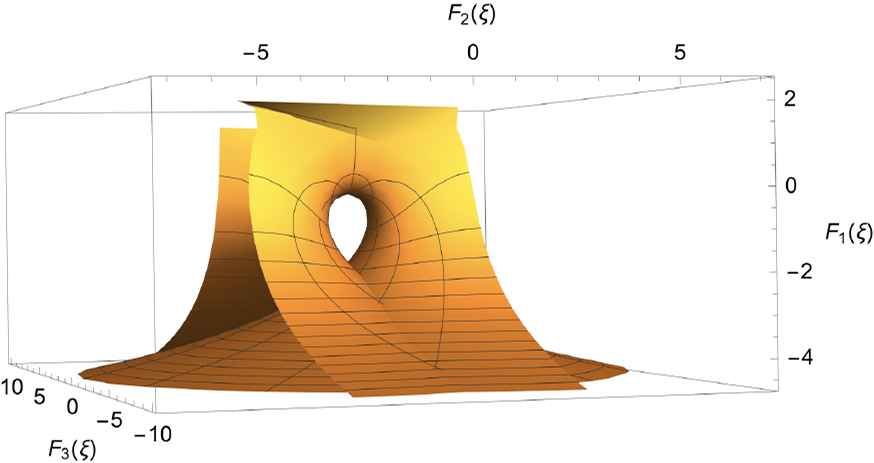
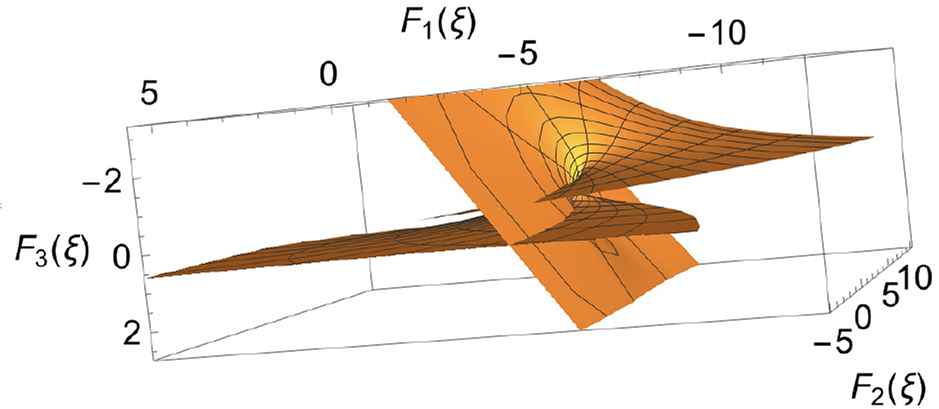
The Gegenbauer equation.
3D numerical display of the Enneper-Weierstrass representation of the surface describing the Gegenbauer equation, obtained by computing ξ0 = 0, ξ = reiθ,

The Jacobi equation.
3D numerical display of the Enneper-Weierstrass representation of the surface describing the Jacobi equation, obtained by computing ξ0 = 0, ξ = x + iy,
4. Concluding remarks
In this paper, we have shown the connection between the linear problem, the reduction of the GW equations to an ODE and the immersion functions of 2D-surfaces associated with classical special functions ODEs (SFODE) describing orthogonal polynomials. These links are summarized by the following diagram
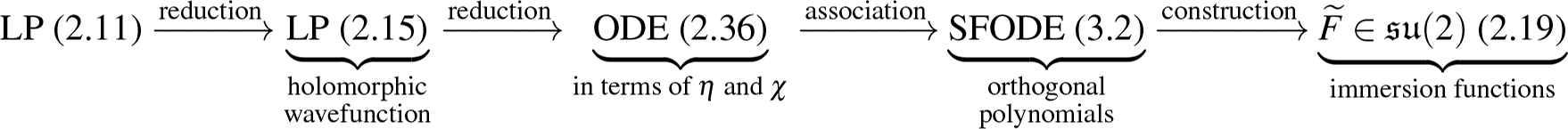
Representation of the relations between the GW equations, the ODE associated with selected special functions and their immersion functions of 2D-surfaces.
This approach allows us to visualize the image of the surfaces arising from specific orthogonal polynomials, reflecting their behavior. The images were generated with Mathematica using the <monospace>ParametricPlot3d</monospace> command (no specific package). In order to reduce the calculation time, the primitive integrals of each component of the surface were used instead of the integral representation of the Enneper-Weierstrass formula.
The existence of SL(2, ℂ)-valued gauge transformations allowed the reduction of the LP to a second-order ODE, which can very often be explicitly integrated in terms of special functions. We showed that the simplification of the LP associated with the moving frame by successive gauge transformations allows the introduction of the arbitrary holomorphic functions η and χ of the Enneper-Weierstrass representation into the problem. This link between the immersion function and the LP was used to determine the second-order linear ODE arising from CMC-λ surfaces. At this point, the ODE representation of the LP could have been associated with any second-order linear ODE. We chose classical ODEs describing orthogonal polynomials, using the degree of freedom corresponding to the fact that the holomorphic functions η and χ are arbitrary. The explicit expressions for the potential matrices and the wavefunction solutions of the LP have been found. This fact enabled the construction of soliton surfaces defined using the Weierstrass or the Sym-Tafel formulas for immersion.
We have formulated easily verifiable conditions which ensure the visualization of surfaces describing special functions. This result can assist future studies of 2D-surfaces with the so-called Askey-scheme of hypergeometric orthogonal polynomials and their q-analogue of this scheme, which can lead to the description of more diverse types of surfaces than those studied in this paper. This task will be considered in a future work.
A new class of minimal surfaces describing orthogonal polynomials has been constructed. These surfaces must now be characterized to enable a clear description of their behavior in order to establish the links between their intrinsic properties and the orthogonal polynomials considered to construct them. The fundamental forms need to be determined, together with the genus and the zeros. We found that the orthogonality interval of the polynomials sometimes describes a curve on the surface. The link between this fundamental interval and the surfaces needs to be studied.
Acknowledgments
V.C. has been partially supported by the Natural Science and Engineering Research Council of Canada (NSERC) and by the Fonds de Recherche du Québec-Nature et Technologies (FRQNT). A.M.G. has been partially supported by the Natural Science and Engineering Research Council of Canada (NSERC) and would like to thank A. Doliwa (University of Warmia and Mazury) and D. Levi (University of Roma Tre) for helpful discussions on this topic.
References
Cite this article
TY - JOUR AU - Vincent Chalifour AU - Alfred Michel Grundland PY - 2020 DA - 2020/09/04 TI - Minimal surfaces associated with orthogonal polynomials JO - Journal of Nonlinear Mathematical Physics SP - 529 EP - 549 VL - 27 IS - 4 SN - 1776-0852 UR - https://doi.org/10.1080/14029251.2020.1819599 DO - 10.1080/14029251.2020.1819599 ID - Chalifour2020 ER -
