A Multi-objective Evolutionary Algorithm with Dynamic Topology and its Application to Network-Wide Flight Trajectory Planning
- DOI
- 10.2991/ijcis.10.1.95How to use a DOI?
- Keywords
- Multi-objective evolutionary algorithm; complex network; flight trajectory planning
- Abstract
Although conventional multi-objective evolutionary optimization algorithms (MOEAs) are proven to be effective in general, they are less superior when applied to solve a large-scale combinational real-world optimization problem with tightly coupled decision variables. For the purpose to enhance the capability of MOEAs in such scenarios, one may consider the importance of interaction topology in information exchange among individuals of MOEAs. From this standpoint, this article proposes a non-dominated sorting genetic algorithm II with dynamic topology (DTNSGAII), which applies a dynamic individual interaction network topology to improve the crossover operation. The dynamic topology and inter-individual interaction are determined by the solution spread criterion in the objective space as well as the solution relationships and similarities in the decision space. The combination of two aspects contributes to the balance of the exploitation and exploration capability of the algorithm. Finally, as an example to real-world applications, the DTNSGAII is used to solve a network-wide flight trajectory planning problem, which demonstrates that the application of dynamic topology can improve the performance of the NSGA-II.
- Copyright
- © 2017, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Effective optimization algorithms are constantly in great need as optimization problems are pervasive in both the fields of science and industry. Many of these real-world problems require a “quality” vector that is usually composed of distinct attributes such as cost and performance. However, these attributes are often in mutual conflict. Because of the conflicting objectives and complicated decision space, it is commonly impossible to find a single optimal solution for such multi-objective problems, but rather a set of solutions known as the Pareto front. Evolutionary algorithms (EAs), being stochastic population-based search methods that simulate the process of evolution, are recognized to be suitable for multi-objective optimization problems (MOP) with the idea of reproduction, recombination, and selection1–3.
For multi-objective evolutionary algorithms (MOEAs), the optimality of solutions should be a minimization of the distance between the solution set and the true Pareto front, while a thorough exploration of the search space should be guaranteed by finding a set of solutions as diverse as possible in the objective space. A series of works has been carried out to investigate the methods to balance the goal of convergence and diversity. However, most of them kept eyes on using the features of the objective vector to control the selection operator by Pareto based rank assignment or sorting schemes, like niche sharing4, hyper grid5, crowding distance6, or based on performance indicators7–9. In fact, a careful design of genetic operators in MOEAs could facilitate the exchange of information between individuals, introduce genetic diversity into the chromosomal pool and convergence to the optimum10. In order to achieve this goal, most works tend to dynamically adjust the probability of genetic operations as e.g. in Ref. 10. Nonetheless, modifying the scheme of mating selection is one of the latest areas to pursue11–14.
In recent studies, complex network structural properties were employed to represent the interaction structure among individuals in EAs15–17, which results in outstanding performance on the benchmarks for one objective optimization problems. However, it has not been verified in more complicated real-world problems. To overcome the weakness of conventional genetic operators in MOEAs that ignore the feature of individual solutions and the interaction structure among them especially when dealing with the real-world problems, this paper proposes a modified crossover mechanism considering the dynamic individual interaction network topology determined by the problem-specific features. This new algorithm is named the non-dominated sorting genetic algorithm II with dynamic topology (DTNSGAII), whose individuals are connected into a directed irregular network. The network degree of individual interaction topology varies dynamically depending on the spread criterion of population in the objective space. Furthermore, DTNSGAII conducts inter-individual interactions according to their relationships and similarities in the decision space.
For empirical study, a network-wide flight trajectory planning (NFTP) problem in China is given to verify the efficacy and the practicability of the DTNSGAII for solving the multi-objective real-world problem. The NFTP aims to reconcile the spatio-temporal contradiction of safety and efficiency existing in current air traffic management systems18. It tries to generate flight trajectory plans over the whole air traffic network with a minimum number of conflicts as well as a minimum amount of trajectory adjustment cost. Considering the large scalability, high complexity, nonlinear and discontinuous characteristics of this specific type of strategic flight planning problems19,20, DTNSGAII is equipped with a problem-specific heuristic to form individual topology. Finally, it is demonstrated that the optimization results obtained by DTNSGAII are more promising than traditional NSGAII.
The rest of the paper is organized as follows: In Section 2, the basic NSGA-II for the multi-objective optimization problem is briefly explained, and an overview of related works that inspire this modified algorithm is given. The next section is devoted to describe our proposed DTNSGAII which utilize the complex networks structural properties. In the 4th section, DTNSGAII is tailored for the optimization of the NFTP problem. We also demonstrated the efficacy of the dynamic topology and the superiority of DTNSGAII over NSGA-II in this section. Finally, in Section 5 the results are summarized.
2. Evolutionary Algorithm For the Multiobjective Optimization Problem
The target of a MOP is to optimize several conflicting objective functions simultaneously. It can be expressed as
MOEAs seek out the Pareto optimal solutions through its stochastic population-based search features and has obvious advantages of addressing discontinuous, non-differential, and non-convex problems in the real-world applications. A number of MOEAs have been developed in the past decades, among whom the NSGA-II6 proposed by Deb et al. is one of the most widely used methods. It uses non-dominated sorting, crowded-comparison approach and elitism selection to greatly reduce the computational complexity, as well as to improve the diversity of the solutions and ensure the convergence. However, the deficiency of NSGA-II is caused by the limitation of the improvement for crossover and mutation operators when dealing with the real-world problems.
The focus of this paper is on the improvement of crossover operations. In relation to this issue, several articles, like Ref. 10, have proposed to investigate the dynamic crossover probability instead of a fixed crossover probability, by first exploring and then exploiting the searching space. This idea reflects the design of a trade-off between convergence and diversity, however, it somehow ignores the interaction structure and the relationship among the populations. To overcome this disadvantage, methods proposed in Refs. 11, 13 and 14 divide the objective space of the optimization problem into fixed sub-regions, and use these partitions as a mating restriction scheme to select the pairs of mating parents. Sun and Shen12 used three different measures of variable distances to control the mating selection. In reality, the decision and objective spaces can be highly complicated, so that merely relying on a single relation between individuals can hardly affect the optimization performance. Therefore, the features of individual, individual relationships and the interaction structure among them, both in the decision space and objective space of the problem, should be taken into consideration. Besides, algorithms that can dynamically solve the problem according to the problem-specific knowledge are necessary when dealing with real-world problems.
3. Non-dominated Sorting Genetic Algorithm II with Dynamic Topology (DTNSGAII)
Crossover is the main new individual generator in the solution space for conventional genetic algorithms. The crossover operator randomly selects two different individuals pair-by-pair to be mating parents from the crossover pool, and the crossover probability is used to determine whether these parents should be combined. The gene information from parents are crossed and combined, then the good characteristics can be passed down to their child. These inter-individual interactions in the population can be interpreted as a complex network, in which the individuals are represented as nodes and when two of them are selected for crossover. The nodes of two as nodes individuals, which are selected for crossover, are then connected by an edge, representing the possible interaction. The produced child will naturally replace one of the parent nodes. The canonical genetic algorithm defines that the crossover could be executed between any two individuals, and the interaction structure can be represented by an undirected fully-connected topology without network node inheritance. This high-density individual interaction network has high average node degree which means, that the produced children have relatively satisfactory spread. However, due to the high randomness, an improvement of quality among the children regarding the target space cannot be guaranteed. A ring-like network with low-density topology might limit the demission of the diversity information but could benefit from the simple connections. Once the selected parent crossover with fit mates, it is more possible to produce offspring of good quality.
Based on the influence of network topology on the produced offspring, the multi-objective genetic algorithm with dynamic topology (DTNSGAII) first uses the spread of solutions in the objective space to control the crossover operation. Afterwards, it decides how many possible information interactions that one individual could make to trade off the exploration and exploitation throughout the optimization process. The algorithm uses the feedback of a spread criterion of the population along the evolution process to modify the node-degree of the network.
The spread criterion is defined as following:
The value of network node degree D varies along with the value of Δ(Pop). When the spread criterion is likely to be small in one generation, we apply the strategy of improving the node degree with the purpose to make the population scattered in future generations. Conversely, if the current population has a satisfactory spread, D will be reduced and the exploitation capability will be emphasized. Briefly speaking, D will vary inversely with Δ(Pop) and can be expressed as shown in Eq. (2):
Network node degree only decides the size of the mating pool of each parent individual. The individual interaction network formulated by the aforementioned scheme is simply a nearest-neighbor coupled network (Fig. 1(a))15 with all nodes sharing the same degree. DTNSGAII can also decide the mating candidates for each parent according to the features and the similarity of solutions in the decision space. To tackle a real-world problem, which always have large-scale and tightly coupled combinatorial decision variables, the coupling relationship and problem-specific knowledge of decision variables can be used to locate the connected neighbors of individuals in the interaction network. A user defined problem-specific mapping procedure M : Ω → Ψ could map any n dimensional variable vector x = (x1,x2,…xn)T ∈ Ω to a k dimensional information vector space Ψ , with the expression z = M(x). z = (z1,z2,…zk)T ∈ Ψ is the information vector and normally has k < n to reduce the problem dimensionality. In this way, the burden of describing the relationship among variable vectors is transferred to the information space. Normally speaking, the mapping procedure M : Ω → Ψ is more capable of describing the proximity or similarity of the variable vectors when using the distances between information vectors. The user can denote all the individuals of the population as z1,z2,…z|Pop| in the information space. According to the definition of M : Ω → Ψ, the user can then determine the adjacent relationship λzi zj between individuals in the individual interaction network. Generally, parent individuals tend to connect to mates with radical differences. Therefore, the chances are increased to combine distinctive genes in the subsequent generation and avoid inbreeding. Furthermore, the possibility of passing down hybrid vigor to the children is improved.
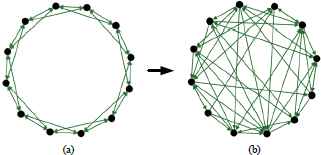
Illustration of an interaction network, consisting of 12 individuals. (a) Nearest-neighbor coupled network with D = 4. (b) Directed irregular network with DO = D = 4.
So far, the interaction network is converted to an irregular network as shown in Fig. 1(b) with the same network density. Noted that the out-degree of an irregular network is DO = D, and the in-degree of each node on the other hand may be diverse but . Two solution spaces that influence the crossover performance have been both taken into consideration to form a dynamic directed interaction network and thus to control the crossover operation. An improvement of the NSGA-II for a better exploration and exploitation capability aiming at real-world problem is realized.
Finally, Fig. 2 lists the pseudo-code of improved crossover operation of the DTNSGAII.

The pseudo-code of improved crossover operator of DTNSGAII.
4. Real-world Application: Network-wide Flight Trajectory Planning
The optimization of a network-wide flight trajectory planning (NFTP) is used in this section as an example to demonstrate the performance of the proposed DTNSGAII for solving a practical engineering problem. The NFTP problem is a constrained MOP which has the characteristics of large scalability, non-linearity and discontinuity, and thus challenging for the conventional MOEAs.19 This particular NFTP problem relates to an air route network (ARN) with the aim of adjusting all the strategic trajectories to operate in a safe environment with the least costs. Traffic management initiatives (TMI), including ground holding, rerouting and flight level allocation, are used in our model to distribute the trajectories induced by traffic demands evenly over time and the 3D airspace. Optimized planning should also guarantee that all airports and flights satisfy their capacity and performance limitations. In this section, we first introduce the model of the NFTP problem. Subsequently, DTNSGAII is adapted to solve the NFTP problem, equipped with a problem-specific heuristic to form the dynamic individual interaction network. The optimization results obtained by DTNSGAII are subsequently shown and analyzed.
4.1. Optimization Model for the NFTP problem
The ARN trajectory planning problem considered can be represented as a layered structure as shown in Fig.3. In the vertical plane, it is divided into several flight levels define within the set L . For each flight level, the horizontal plane is a directed graph (N, A) where N is the set of nodes (airports and crossing waypoints CW are surround by conflict region CR surrounded, which are depicted as red circles in Fig.3), while A is the set of arcs (air routes).21 The set CW includes all airborne waypoints. Any CW constitutes a CR, but the radius of CRs are different. A reasonable value for the size of a CR is determined in dependency of various factors, like e.g. the separation standard or the angle of intersecting routes. Besides, a temporal discretization has been applied to the problem model. The sampling duration Ts of discrete time-slots in set T is defined by users. Once the ARN is given as well as flight f along with its route rf, departure time
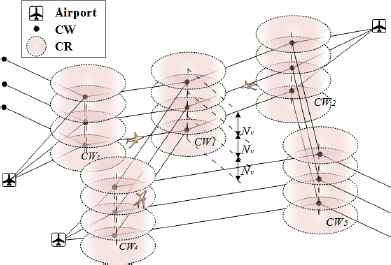
Illustration of the ARN.
The intersecting or overlapping trajectories may induce conflicts when aircraft are close to each other in the same CR. The main target in safe ATFM is the minimization of potential airborne conflicts.
To avoid as many potential conflicts with other aircraft as possible, the reference trajectory of a flight could be significantly modified by TMIs thus deviating far from the original plan. However, the cost of solving potential conflicts also needs to be evaluated from an economical perspective. Essentially, we propose to minimize a combination of three trajectory modification cost components and maintain equity among the modified flights. The objective function can be expressed as
Considering efficiency, equity, and aircraft performance, each element in a trajectory should be as close as possible to their scheduled value. The model’s constraints sets are as follows:
The constraints set in Eq. (6) claim that the range of route changes for flight f should be within Rf, which is the set of routes available, and note that the original route is normally the shortest route for f. The constraints set in Eq. (7) stipulate that each flight can change its level at most
4.2. Full Details of DTNSGAII for the NFTP
The problem-specific mapping procedure M : Ω → Ψ of DTNSGAII first transforms each combination of decision variables into an information variable. For the NFTP problem model, the interaction between flights fi and fj, i.e., ϕij, is defined as follows:
Note that ϕji and ϕij may not be equal, i.e., the matrix. Matrix Φ = [ϕij]|F|*|F| is asymmetric. Summation over row i of matrix Φ represents a measurement of the total spatial-temporal overlap degree between flight fi and all the other flights, defined as TI value
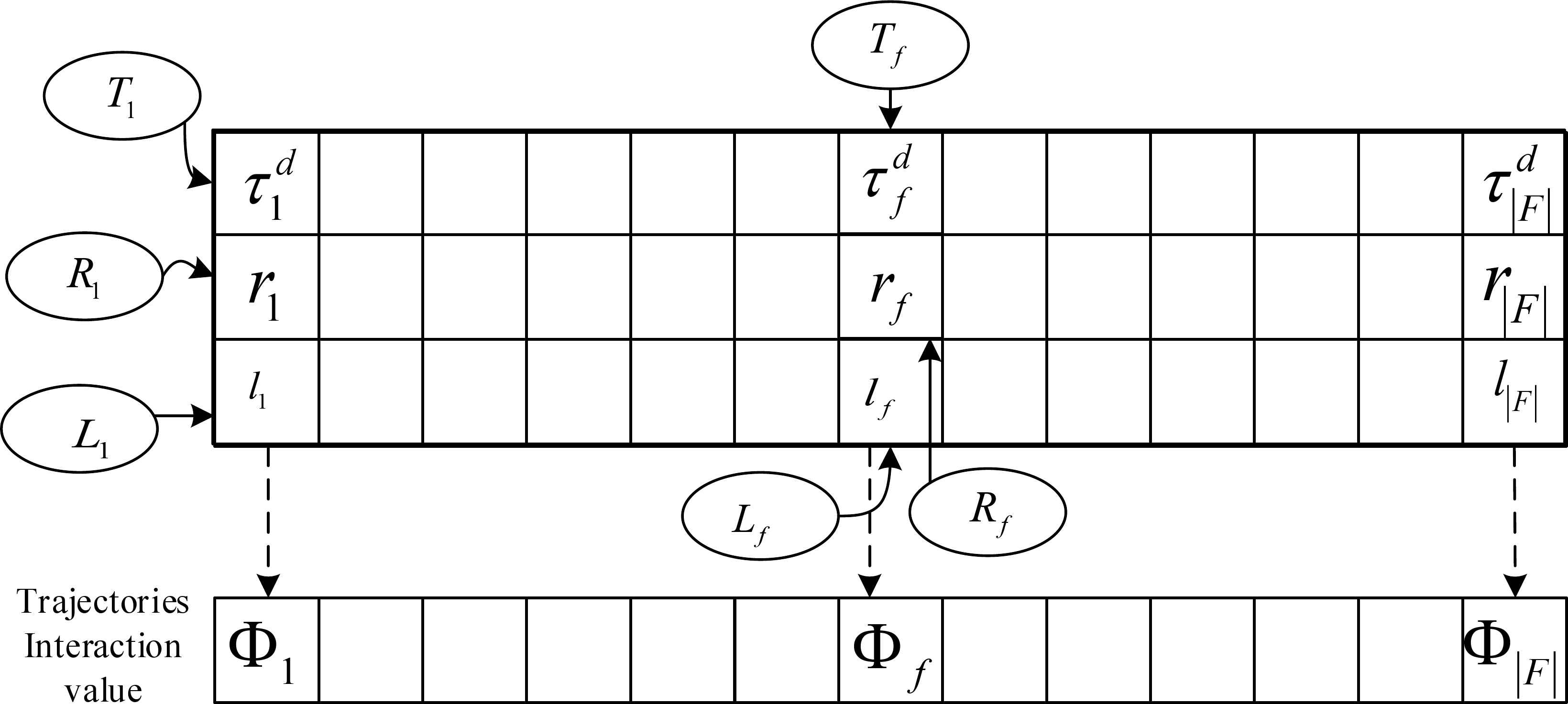
Exemplary encoding of the encoding of a chromosome and the vector in information space.
Next, each individual can be mapped to a point in a |F| -dimensional information vector space Ψ as a vector (Φi1,Φi2,…Φi|F|). The distance ∥dij∥ between points describes the similarity of two individuals in the variable space, which are regarded as λzizj in DTNSGAII. For any given individual i , all other individuals are sorted in descending order according to ∥dij∥.
Unfortunately, there can be no certainty that genetic operators always generate feasible solutions. If any violation happens on a particular gene, it will be set to a closest boundary value of the corresponding set according to Eqs. (6)–(9) in DTNSGAII.
4.3. Optimization Performance
Two parts of computational experiments are hierarchically carried out to demonstrate the contribution of this paper for solving the NFTP problem in this subsection. The influence of the dynamic degree of individual interaction network alone on the performance of the optimization are shown firstly. Next, the effectiveness of integrated DTNSGAII with the directed dynamic network is verified. The domestic flight plan data of China we used for the experiments were extracted from an existing flight schedule database (data courtesy: Aviation Data Communication Corporation, Beijing) of December 3rd, 2015 from 0800-1200 a.m.
For all test cases in the following comparisons, a constant population of randomly generated 100 individuals is used and the optimization process is continued for up to 200 evolution generations. The values for the crossover and mutation probability are 0.9 and 0.1, respectively. Due to the stochastic nature of the algorithm, each test problem is solved 10 times and the averaged performance metrics are compared.
The algorithms were all implemented in C++, and the experiments were performed on a Windows Server with 2.10GHz CPU and 16GB of RAM. All the outcomes were collected on the basis of 20 independent runs. To normalize each part of Eq. (5) which has different definitions for the same cost unit, the problem parameters are set as p = 1 , q = 3 , MGH = 2 , MAH = 2 , MFL = 3 , Ts = 20s to adapt the model optimally to the conditions of the Chinese airspace and the survey of airline costs21.
4.3.1. The effect of DTNSGAII with dynamic nearest-neighbor coupled network topology
Three experimental cases with different ARN sizes and operation scales are:
Case 1: Small size ARN with 20 airports, around 500 CWs; 156 flights which depart during 0800-1100 a.m.
Case 2: Medium size ARN with 50 airports, more than 700 CWs; 334 flights which depart during 0800-1200 a.m.
Case 3: Large size ARN with 115 airports, more than 1600 CWs; 536 flights which depart during 0800-0900 a.m.
The most favorable indicator called the Hypervolume indicator (IH)22 for assessing MOEAs is used to quantitatively evaluate the compared cases and the proposed algorithm. The metric IH takes into account both the convergence and diversity situation, reflecting an overall quality of the obtained non-dominated set. To better exhibit the optimization performance for the NSGA-II with different interaction network node degree, normalized IH are computed for the three cases in Fig. 5. Because of the randomness of the crossover operation and the effect of selection of NSGA-II, no fixed best value of D exists for all the cases, which matches the feature of stochastic optimization. However, according to the distribution of relatively high IH values, reasonable weighting factors a, b are chosen for fitting the dynamic function in Eq. (2) for different cases. The dynamic results of the three cases turns out to outperform the fixed results. The node degree D controlled by the varying diversity measure accomplishes a better IH due to the fact that a dynamic D affects the convergence of the population and retains the diversity to a certain extent.
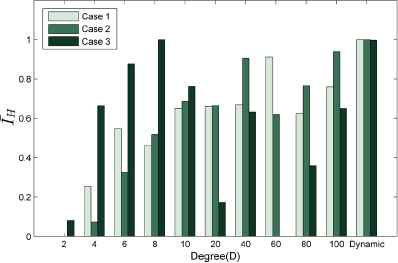
Average normalized IH from 10 independent runs of three cases with different network node degree as well as dynamic degree.
Taking case 1 as an example to verify this observation, the curves depicting the variation of the average spread values throughout the evolution for D = 2 (ring network), D = 100 (fully-connected network) and for D based on a dynamic function with a = 0.0055 , b = 141. One of the curves in Fig. 6 also shows the variation of average dynamic D. When D is large, information is disseminated too fast in the initial period of evolution and an optimum area is quickly located, but the exploitation reduces the spread of the whole population in the middle and late phases of the evolution. When D is small, the spread value remains at a stabilized level since better genes are not totally disseminated and copied, and thus may lead to unsatisfactory convergence results. A dynamic D finds a balance between these two characteristics and moderated the information transmission speed of the individual interaction network. In the beginning of the evolution, the initial population is spread well out in the objective space. The node degree D should be reduced to moderate the exploration and exploitation. The diversity of the population is decreasing along with the evolution process; the optimization converges to the Pareto front but might converge to the wrong area. To fix this phenomenon, the value of D is increased to improve the distribution of the population. Clearly this process feedbacks to control the spread changing through the evolution and finally influences the quality of the solutions as shown in Fig. 5.
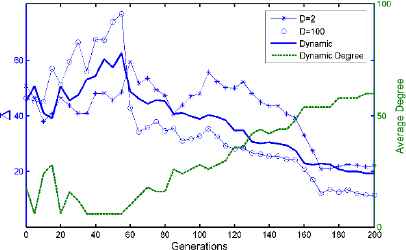
Evolution curves of the average Δ from 10 independent runs when D = 2 , D = 100 and network degree is dynamic, as well as the variation of average dynamic degree.
4.3.2. The effect of DTNSGAII with directed irregular dynamic network topology
The contribution of DTNSGAII has two aspects. The aforementioned analysis of dynamic D only checks the influence of the different quantities of possible crossover individuals. An integrated individual interaction network needs to be a directed irregular network with dynamic DO which also lists the specific crossover individuals according to their relationship in the decision space. As long as the information comes from both the decision and objective space, DTNSGAII demonstrates a more superior performance. In Fig.7, triangle solutions are non-dominated solutions of a simplified version of DTNASGII, where the interaction network is a nearest-neighbor coupled network that does not contain complicated adjacent relationship between each individual. Compared to NSGA-II, the algorithm considering individual interaction relationship outperforms the others on effectiveness for fitter solutions. Without the limitation of the nearest-neighbor coupled network topology, the non-dominated solutions would be better.
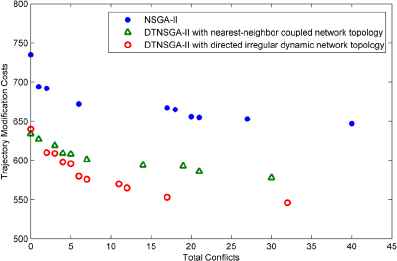
Non-dominated solutions obtained by the compared algorithms over 10 independent runs.
Besides the direct perception from Fig.7, the efficiency of the three algorithms also has been analyzed. The growth curves of IH as the evolution of generations are plotted in Fig.8. With the same initialization, all algorithms have similar evolution trends but at different convergence rates. The simplified version of DTNASGII clearly shows a higher efficiency than NSGA-II. Besides, since it is confined to the nearest-neighbor coupled network topology to the crossover operation, the simplified version of DTNASGII falls behind the DTNSGAII with directed irregular network topology until the evolution goes to the midterm. As demonstrated by the red lines and the red circles in Fig.7, it is beneficial to increase the possibility for a parent to combines genes with mates which show radical difference. The DTNSGAII with directed irregular network topology avoids inbreeding and increases the possibility of passing down hybrid vigor to children in the beginning of the evolution. Although at the cost of losing the preemption, this diversity-keeping and information-controlling method enables DTNSGAII to outperform other alternatives in the end, which caters to the operational need of the industry that tends to focus more on a superior optimization outcome.
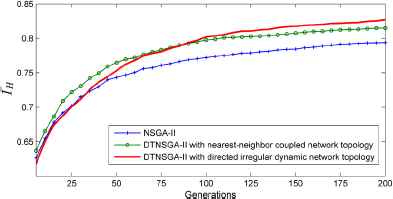
Evolution curves of the average IH for the compared algorithms from 10 independent runs.
5. Conclusion
The conventional NSGA-II overlooks the feature of individual solutions and the interaction structure among them, and therefore encounters challenges in solving large-scale complicated real-world problems. To address this issue, this paper developed a DTNSGAII algorithm, where individuals are connected into a directed irregular network. The network degree of individual interaction topology varies dynamically according to the spread of population in the objective space. In the meantime, DTNSGAII conducts crossover according to individual relationships and similarities in the decision space. The application of dynamic topology was demonstrated to balance the needs of diversity maintenance and convergence capability of the algorithm when solving the NFTP problem. Although preliminary results are promising, DTNSGAII was tailored to resolve one particular problem. In future research, it is also worthwhile to investigate other dynamic patterns of the individual interaction topology to improve applicability and effectiveness of the DTNSGAII.
Acknowledgements
This work is supported by the National Natural Science Foundation for Young Scientists of China (Grant No. 61401011) and National Sci-Tech Support Program (Grant No. 2015BAG15B01).
References
Cite this article
TY - JOUR AU - Su Yan AU - Kaiquan Cai AU - Majed Swaid PY - 2017 DA - 2017/06/22 TI - A Multi-objective Evolutionary Algorithm with Dynamic Topology and its Application to Network-Wide Flight Trajectory Planning JO - International Journal of Computational Intelligence Systems SP - 1345 EP - 1354 VL - 10 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.10.1.95 DO - 10.2991/ijcis.10.1.95 ID - Yan2017 ER -
