Evolutionary Multi-objective Optimization for Multi-depot Vehicle Routing in Logistics
- DOI
- 10.2991/ijcis.10.1.94How to use a DOI?
- Keywords
- Multi-depot vehicle routing; multi-objective optimization; evolutionary algorithm; local search
- Abstract
Delivering goods in an efficient and cost-effective way is always a challenging problem in logistics. In this paper, the multi-depot vehicle routing is focused. To cope with the conflicting requirements, an advanced multi-objective evolutionary algorithm is proposed. Local-search empowered genetic operations and a fuzzy cluster-based initialization process are embedded in the design for performance enhancement. Its outperformance, as compared to existing alternatives, is confirmed by extensive simulations based on numerical datasets and real traffic conditions with various customers’ distributions.
- Copyright
- © 2017, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
The Internet shopping enjoys a surge of popularity in recent years, supported by the advances of mobile communications and Internet technology. For a one-day global shopping event, it could generate gross merchandise value up to USD17.8 billions1. The huge amounts of transactions imply billions of goods need to be delivered to customers all over the world in an efficient way, which is an opportunity and also a challenge for the logistics industry.
In face of the challenge, many research efforts have been made, while vehicle routing problem (VRP)2,3 is a related topic in operational research, focusing on domestic delivery. Given a depot, vehicles are to visit different sites of customers for once. VRP can be generalized as problem with multiple depots, referred as multi-depot vehicle routing problem (MDVRP)4,5. In MDVRP, customers are firstly assigned to one of the depots, and the vehicle at the depot is deployed to serve the dedicated set of customers based on a designated routing path.
To better reflect the practical conditions, many variants of VRP and MDVRP have been suggested. For example, by considering the limited capacity of a vehicle, one obtains a classic capacitated vehicle routing problem2. In Ref. 4, two types of vehicles, delivery vehicle and installation vehicle, are employed, where the time window restriction on delivery and onsite service time of installation vehicle are considered. Heterogeneous depots have also been included according to commercial offers, motivated by the market segmentation, as described in Ref. 5. In Ref. 3, desynchronized arrivals are assumed in VRP, as a result, the queuing of parcels has to be managed to avoid congestion in delivery.
In this paper, we focus on the MDVRP with delivery service time. Since a customer site now serves as a collection point of parcels for a set of clients, the delivery service time becomes comparable to the transportation time. Unlike the installation service time considered in Ref. 4, which is only included as an additional constraint, we incorporate the service time in the objective function, to truly reflect the total delivery period. In addition, as demonstrated in our results, the delivery service time would magnify the impact of customer distribution on algorithmic performance, making the conventional distance-based customer assignment methods less attractive.
MDVRP is proved to be NP-hard and usually involves multiple objectives. To cope with such a complex and difficult multi-objective problem (MOP), meta-heuristic algorithms, such as tabu search6,7 and evolutionary algorithms8,9, are commonly adopted. Moreover, local search mechanisms have also been employed10,11, while, for further improvements, hybrid approaches combining evolutionary algorithms and local searching mechanisms12,13 seem to be promising.
Here, a hybrid multi-objective evolutionary algorithm (HMOEA) is proposed. To enhance its searching capability, a fuzzy cluster-based initialization incorporating customers’ density and distance, an ordered-based cut-and-paste operation and a two-phase local search are newly designed. The effectiveness of the design is also verified by extensive simulations based on real-world traffic data.
The rest of the paper is organized as follows. In Section 2, MDVRP with customer service time is formulated. The proposed HMOEA is then explained in Section 3 in details. Simulation results and discussions are made in Section 4, and finally, the work is concluded in Section 5.
2. Problem Formulation
In MDVRP, a set of N customers (𝒱c) is to be served by a set of M depots (𝒱d). Based on their locations, the transportation network and traffic conditions, a fully-connected directed graph, 𝒢 = (𝒱, ℰ, 𝒜), can be formulated, where 𝒱 = 𝒱c∪𝒱d is the set of nodes, ℰ = {(i, j)|i, j ∈ 𝒱 ,i ≠ j} is the set of edges and and 𝒜 = {(dij, τij)|(i,j) ∈ ℰ} is the set of weights for the edges with di j and τi j being the traveling distance and duration from node i to node j, respectively. The traveling duration is time-dependent related to real-time traffic conditions and the traveling distance is fixed. Also, di j ≠ dji and τi j ≠ τji.
In this work, it is assumed that each depot can invoke at most one vehicle, while all the vehicles are homogeneous and have sufficient capacity. To reflect the transportation efficiency and customers’ satisfaction, two primary criteria, namely the total traveling distance (f1) and maximum delivery duration (f2), are considered. A multi-objective MDVRP (MO MDVRP) is hence constructed as follows:
3. Design of Hybrid MOEA (HMOEA)
In order to effectively manage the MO MDVRP specified in Section 2, a hybrid multi-objective evolutionary algorithm (HMOEA) is proposed. Its flow diagram is given in Fig. 1 and the major designs are explained below.

Flow diagram of HMOEA.
3.1. Chromosome representation
Encoding the solution by chromosome is always a key step in the design of an evolutionary algorithm (EA). In MDVRP, two sub-design tasks are involved. One is to assign customers to one of the depots while the other is to find the best route for serving the set of customers in each depot. Therefore, an ordered chromosome14 is suggested.
The chromosome is encoded as an integer string with a length of (N + M − 1). Without loss of generality, the numbers 1 to N denote the customers while (N + 1) to (N + M − 1) serve as separators. An illustrative example is given in Fig. 2. The chromosome in Fig. 2 (a) consists of 12 customers and 3 separators. It can thus define the assignment of customers to 4 depots {A,B,C,D} and also the route of each vehicle as indicated in Fig. 2 (b).
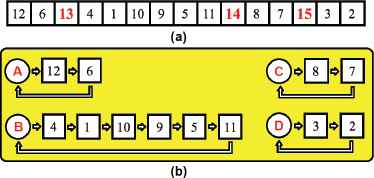
(a) Ordered chromosomes for 12 customers and 4 depots (b) Resultant route for each depot.
3.2. Population initialization
After defining the chromosome, the first step in HMOEA is to generate the initial population. Although randomly generated population is common, the preference of having a better set of initialized population has also been discussed in EA communities. In Ref. 12, chromosome is configured by assigning customers to the nearest depot. Such a binary decision is modified into a fuzzy one in Ref. 15, and a customer can have different levels of belongings to all the depots, governed by the following membership function (MF)
Although such a distance-based initialization method would facilitate the search of solutions, the impact of customer distribution is totally ignored. It can be easily imagined that, if too many customers are assigned to a depot, it may not be a good choice.
Hence, a new MF is proposed as below:
A new fuzzy cluster-based initialization (FCBI) process can then be designed to obtain a population
Set 𝒫i = ∅ |
Obtain 𝒞k for k = 1,2,⋯ ,M by assigning customers to the closest depot; |
Compute ρk for k = 1,2,⋯ ,M with α = αi using (10); |
for j = 1 to N |
Compute ujk for k = 1,2,⋯ ,M using (9); |
Find k′ s.t. k′ = arg maxk∈𝒱dujk; |
Update 𝒞k, 𝒞k′ s.t. 𝒞k = 𝒞k\{j} and 𝒞k′ = 𝒞k′∪{j}; |
Update ρk for k = 1,2,⋯,M using (10); |
end |
for p = 1 to Pi |
for each 𝒞k with k = 1,2,⋯ ,M, generate routing path by sequential sampling algorithm probabilistically16; |
Encode the solution as a chromosome I; |
Update 𝒫i by 𝒫i = 𝒫i∪{I}; |
end |
Pseudo code for FCBI.
3.3. Selection process
After generating the initial population and evaluating the objective functions f1 and f2 for each chromosome, genetic cycles are repeated until termination criteria are met. In each cycle, parents are selected from the current population and used to generate offspring via some genetic operations. Offspring will further be improved by a two-phase local search. The elites in the current population and offspring population are then preserved to form the next population.
To better cope with the MO MDVRP, we adopt the tournament selection as suggested in the non-dominated sorting algorithm (NSGA-II). The two randomly selected chromosomes in a tournament are compared using Pareto dominance and crowding distance and the better one is selected as parent. Their operational details can be found in Ref. 17 and are omitted here due to page limitation.
3.4. Genetic operations
3.4.1. Order-based cut-and-paste
The cut-and-paste (CP) operation in JGGA18 is well-known for its excellence in new solution exploration. Here, CP is modified for ordered chromosome and it is referred as order-based cut-and-paste (OCP). As shown in Fig. 3, a segment of genes is randomly selected from a parent, say Parent A, and inserted at a random site of another parent, Parent B. An offspring is then obtained by removing repeated genes. Another offspring can be obtained by swapping the roles of Parents A and B. In our work, the operational probability of OCP is governed by pc.
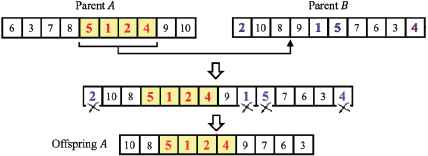
An example of order-based cut-and-paste.
3.4.2. Integration of mutation operators
To prevent trapping in local minima, three mutation operations are integrated and applied to the offspring. The first one is gene swapping, in which two genes are randomly selected and swapped. (Fig. 4(a)). The second one is referred as inversion. A portion of genes is randomly selected and their positions are inverted (Fig. 4(b)). The last one is called self OCP, which is to apply OCP onto the same offspring (Fig. 4(c)). In this work, same operational rate is used and given by pm.
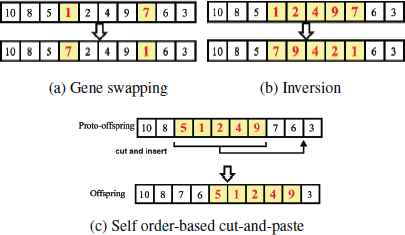
Examples of the three mutation operators.
3.5. Two-phase local search
To effectively tackle with the MO MDVRP, two local searching mechanisms are applied to further improve each offspring, targeting the two key processes in the optimization, i.e. the path routing and the customer assignment, respectively.
3.5.1. 2-opt solver
The first local search is based on 2-opt solver, which is originally suggested in Ref. 19 for the traveling salesman problem. It is to reduce routing path length by replacing two non-adjacent arcs with two other arcs. Its operational procedures are given in Table 2 and a simple illustration is depicted in Fig. 5. Consequently, the routing path is modified by 2-opt whenever there is a reduction of path distance.
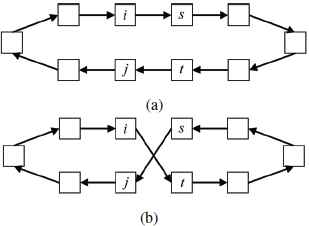
Illustration of 2-opt solver. Modification of route due to the condition: pL(i, j) in (a) > pL(i, j) in (b).
Extract M routing paths for M depots from chromosome I; |
for k = 1 to M |
for each (i, j), where i, j ∈ 𝒞k, prec(j) ≠ i, |
Let s = succ(i); t = prec(j); |
if (dit + pL(t,s) + dsj < pL(i, j)) |
Set succ(i) = t, prec(j) = s; Reverse p(s,t) to p(t,s); |
end |
end |
end |
Encode the improved solution and replace I; |
Note: prec(i) and succ(i) returns the preceding and succeeding nodes of i along the path. p(i, j) and pL(i, j) represent the path from i to j and its length, respectively.
Pseudo code for 2-opt solver.
3.5.2. Customer grouping optimizer
The second local search is an inter-route operator called customer grouping optimizer (CGO). We define the delivery duration of a routing path of the vehicle at depot k as
CGO is designed to reduce maxk∈𝒱d(DDk) by moving unbefitting customers from customer set 𝒞p with p = arg maxk∈𝒱dDDk, to smaller sets, without compromising the other objective, i.e. the total traveling distance. The general idea is illustrated in Fig. 6. Consider the customer t ∈ 𝒞p, which has the most significant impact in DD, i.e. (τst + τtu − τsu) is maximum where s = prec(t) and u = succ(t). If there exist i ∈ 𝒞q and j = succ(i), such that (dit + dt j − di j ⩽ dst + dtu − dsu), customer t will be re-assigned to 𝒞q, s.t. t = succ(i) = prec(j). This operation will be repeated for r times if CGO is carried out, governed by a probability of pu. The choice of r is determined by compromising the speed and the performance. In our simulations, r is set as 15, and generally, the larger the searching space is, the larger r should be.
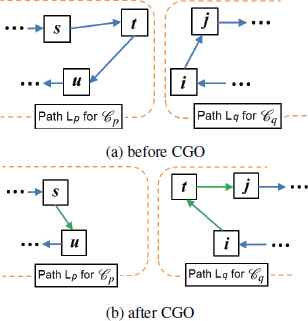
Illustration of CGO.
4. Experimental Results
4.1. Testing cases and HMOEA parameters
In our simulations, two testing cases, 𝒢A and 𝒢B, are considered. For each case, M = 6 depots of a major logistics company in HK, mainly located in Kowloon City and Yau Tsim Mong districts are selected. N = 100 customers are served, with their locations distributed uniformly and non-uniformly for Cases 𝒢A and 𝒢B, respectively. Figures 7(a) and 7(b) show the locations of customers and depots for the two cases. The traveling distance di j and traveling duration τi j for any (i, j) ∈ ℰ are derived from Google Maps Distance API, to reflect the real time traffic condition. Also, the parameters used in HMOEA are listed in Table 3.
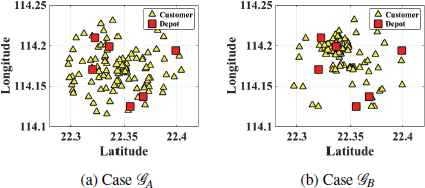
Locations of customers and depots in 𝒢A and 𝒢B.
| Population size (|𝒫|) | 100 |
| Probability of crossover (pc) | 0.9 |
| Probability of mutation (pm) | 0.2 |
| Probability of grouping optimizer (pu) | 0.5 |
| Number of Offspring (|ℒ|) | 50 |
General parameter settings of HMOEA.
4.2. MO performance metric
In MO optimization, the goodness of a non-dominated solution set can be measured by two metrics, namely the convergence and the diversity18.
The convergence metric is defined as
The diversity implies the non-uniformity and spread in the distribution of the non-dominated solution set. It is computed by
Since the true Pareto optimal front is not available for our problem, a reference set is used instead. It is obtained by merging results from 5 runs of HMOEA (with 200,000 generations) and all the other compared methods.
4.3. Design Verification
4.3.1. Effectiveness of FCBI
We firstly investigate the effectiveness of the fuzzy cluster-based initialization (FCBI). It is compared to two common approaches, namely the distance-based (DBI) initialization and random initialization (RI).
In DBI, customers are assigned to the closest depot, while the routing path of each customer set is then generated by applying sequential sampling algorithm probabilistically. In RI, chromosomes are simply randomly generated.
FCBI, DBI and RI are used to generate the initial populations for NSGA-II, respectively, with order crossover and integrated mutation operator equipped. The average results over 20 runs are tabulated in Table 4. Since the influence of initialization tends to diminish against generations, the non-dominated solution sets obtained at the 4,000th generation are compared.
| FCBI(μ,σ) | DBI(μ,σ) | RI(μ,σ) | ||
|---|---|---|---|---|
| 𝒢A | β | (1.298, 0.203) | (1.616, 0.468) | (3.480, 0.380) |
| γ | (0.822, 0.136) | (0.992, 0.128) | (1.062, 0.252) | |
| 𝒢B | β | (0.391, 0.201) | (0.774, 0.280) | (0.957, 0.439) |
| γ | (0.907, 0.285) | (1.045, 0.206) | (1.159, 0.249) |
Comparisons of different initialization methods based on performance metrics β and γ. μ and σ are the mean and standard deviation of performance metrics, respectively, and the best is in bold.
As shown, FCBI performs the best in all cases, except that its σγ is slightly larger than that of DBI. However, since μγ(FCBI) is smaller, it can still conclude that FCBI is better than DBI.
We also notice a significant improvement in Case 𝒢B when FCBI is employed. Comparing to RI, the improvements by DBI for Case 𝒢A and 𝒢B are 53.56% and 19.16%, respectively. While if FCBI is used, the improvements become 62.71% and 59.10%, respectively, confirming the ability of FCBI in managing various customer density distributions.
4.3.2. Effectiveness of OCP
Under the framework of NSGA-II, we directly compare OCP with other conventional order-based crossovers, including order crossover (OX) and partially mapped crossover (PMX), for solving MO MDVRP. Table 5 summarizes the comparisons of results (average of 20 runs) of NSGA-II with these crossover operations, terminated at 150,000 generations. As shown, OCP performs the best, except that its μγ is slightly larger than that of OX. However, its σγ is smaller, indicating a better consistency. PMX is the worst as it emphasizes absolute positions of genes, while for MDVRP (or general VRP), relative positions of genes are much more important.
| OCP(μ,σ) | OX(μ,σ) | PMX(μ,σ) | ||
|---|---|---|---|---|
| 𝒢A | β | (0.729, 0.264) | (0.810, 0.279) | (0.989, 0.349) |
| γ | (0.742, 0.079) | (0.736, 0.097) | (0.800, 0.091) | |
| 𝒢B | β | (0.072, 0.023) | (0.111, 0.084) | (0.218, 0.060) |
| γ | (0.720, 0.066) | (0.738, 0.088) | (0.792, 0.079) |
Comparison of different crossover operations
4.3.3. Effectiveness of two-phase local search
Lastly, we investigate the effectiveness of the two-phase local search (TPLS). The non-dominated solution sets obtained by HMOEA with and without TPLS are plotted in Fig. 8.
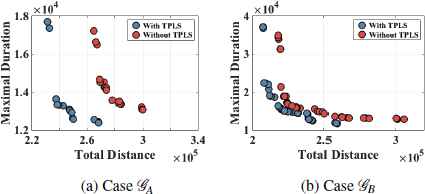
Non-dominated solution sets obtained by HMOEA with and without TPLS. The sets are collected when there is no further update in last 1,000 generations.
In both cases, the inclusion of TPLS enhances the searching of non-dominated frontier. Moreover, as shown in Tables 4 and 5, β is much larger in Case 𝒢A than in Case 𝒢B, meaning that it is a more difficult problem. This is also confirmed in Fig. 8. It fails to locate non-dominated solutions in Case 𝒢A if TPLS is excluded. In contrast, improvement in non-dominated solution set is relatively small in Case 𝒢B.
4.4. Comparisons of Algorithms
Finally, HMOEA is compared to NSGA-II and SPEA-II20, which are both well known for effectively approximating optimal solutions and maintaining the diversity of non-dominated frontier. The design of NSGA-II in Ref. 9 is adopted and it is equipped with DBI, one-point crossover and gene swapping mutation. For SPEA-II, RI, OX and gene swapping mutation are used. All other parameters of these three algorithms are kept the same for fair comparison.
Table 6 shows the average results of 10 runs of the above algorithms, each of which terminates after 150,000 generations. Both μβ and μγ of HMOEA are the smallest in the two testing cases, indicating the best quality of the solutions. The standard derivations are slightly worse, but with the fact that μ is much smaller, the outperformance of HMOEA is confirmed.
| HMOEA(μ,σ) | NSGA-II(μ,σ) | SPEA(μ,σ) | ||
|---|---|---|---|---|
| 𝒢A | β | (0.607, 0.235) | (1.312, 0.132) | (2.435, 0.405) |
| γ | (0.792, 0.161) | (0.833, 0.104) | (1.093, 0.065) | |
| 𝒢B | β | (0.067, 0.064) | (0.168, 0.075) | (0.271, 0.313) |
| γ | (0.752, 0.166) | (0.814, 0.059) | (1.034, 0.143) |
Comparison of different evolutionary algorithms
Due to the inclusion of local search, the computational time of HMOEA is longer. For one generation, HMOEA takes 16.84 ms while NSGA-II and SPEA-II need 4.43 ms and 3.49 ms, respectively, in a PC platform with Intel Core i5 (2.6 GHz) and 8G RAM. However, as shown in Fig. 9, when comparing the non-dominated solution sets obtained with a fixed run-time, HMOEA still performs superior than the others, confirming the effectiveness of our design.
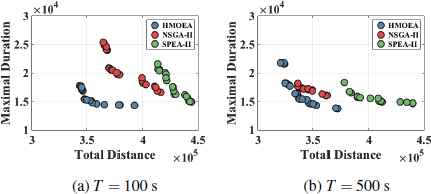
Non-dominated solution sets obtained by different EAs with total run-time T. The sets are obtained by merging results of 10 runs.
5. Conclusion
In this paper, a hybrid multi-objective evolutionary algorithm, called HMOEA, is designed to address the multi-depot vehicle routing problem with delivery service time. New operations, including fuzzy cluster-based initialization, order-based cut-and-paste and two-phase local search, are proposed and implemented. Their effectiveness in exploration and handling various customer location distributions is confirmed by extensive simulations based on real traffic data. The simulation results also confirm that HMOEA outperforms other existing methods in solving the multi-depot vehicle routing problem.
Acknowledgments
This paper was supported by grants from City University of Hong Kong (7004608 and 7004835).
References
Cite this article
TY - JOUR AU - Xiaowen Bi AU - Zeyu Han AU - Wallace K. S. Tang PY - 2017 DA - 2017/09/14 TI - Evolutionary Multi-objective Optimization for Multi-depot Vehicle Routing in Logistics JO - International Journal of Computational Intelligence Systems SP - 1337 EP - 1344 VL - 10 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.10.1.94 DO - 10.2991/ijcis.10.1.94 ID - Bi2017 ER -
