Cascades Tolerance of Scale-Free Networks with Attack Cost
- DOI
- 10.2991/ijcis.10.1.93How to use a DOI?
- Keywords
- Network robustness; Cascading failures; Genetic algorithm; Attack cost
- Abstract
Network robustness against cascades is a major topic in the fields of complex networks. In this paper, we propose an attack-cost-based cascading failure model, where the attack cost of nodes is positively related to its degree. We compare four attacking strategies: the random removal strategy (RRS), the low-degree removal strategy (LDRS), the high-degree removal strategy (HDRS) and the genetic algorithm removal strategy (GARS). It is shown that the network robustness against cascades is heavily affected by attack costs and the network exhibits the weakest robustness under GARS. We also explore the relationship between the network robustness and tolerance parameter under these attacking strategies. The simulation results indicate that the critical value of tolerance parameter under GARS is greatly larger than that of other attacking strategies. Our work can supply insight into the robustness and vulnerability of complex networks corresponding to cascading failures.
- Copyright
- © 2017, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Complex networks have been found to be effective to describe many networked systems in nature and society, such as the Internet, power grids and communication systems, and so on. Over the past few decades, complex network research has made great achievements in many areas 1,2, including network modeling 3,4,5, evolutionary games 6,7, optimization8, epidemic spreading 9 and traffic dynamics 10,11,12, etc.
Because of the great importance of vulnerability and robustness for many real-world complex networks, the robustness of networks has attracted many researchers in recent years 13,14,15. In particular, the problem of cascades with load redistribution on networked systems has aroused widespread concern 16,17,18,19. Some important aspects of cascades have been extensively researched, including the models for describing the cascading failures20,21,22, the defense and control strategies for cascades 23,24,25,26, the cascading models in real networks 27,28,29. Motter et al. 20 put forward a global load-based cascading model. The authors shown that, in the case of attack triggered by breaking down a single vital node, the heterogeneity of complex networks can make them extraordinary fragile. Subsequently, by proposing a mechanism of local weighted flow redistribution, Wang and Chen 30 studied the cascade phenomena on weighted networked systems. They found that the strongest robustness level of weighted complex network is accomplished when the link weight equals to kikj, where ki and kj are the degrees of the vertexes linked by the edge. Recently, Wang et al. 18 proposed a simple cascade model and investigate cascade phenomena triggered by breaking down the highest-load node in complex networks. They found that the fluctuations of cascading dynamics in networks is abnormal and the resilience of networks against cascades decreases inversely when the node’s capacity increases.
However, most previous works of network robustness assume that the attack cost is the same 31,32. Actually, for many real-world networks, the removal cost of a link or a node may be quite various 33. In this paper, the factor of attack cost is merged into the cascading failure model and the cost of breaking down a node is related to its degree. The results indicate that the network robustness against cascading failures is heavily affected by the node’s attack cost, and the genetic algorithm removal strategy (GARS) displays a better performance than other attacking strategies.
This paper is organized as follows. In the section 2, we describe the attack-cost-based cascading failure model and node attacking strategies specifically. Simulation results and correspondent theoretical analysis are provided in Section 3. Finally, our conclusions are drawn in section 4.
2. The model
2.1. Network model
It is known that many real-world networks display a scale-free property, for example the Internet, WWW and transportation networks 34,35. In this paper, we use the Barabási-Albert (BA) network 5 to explore the cascades tolerance of scale-free complex networks. The BA network is generated by growth and preferential attachment rules, which can be found in many realistic networks. Starting from m0 fully linked nodes, at each time step one new node will be added to the BA network model. The new one is preferentially linked to m (m ⩽ m0) old ones with the probability Πi = ki/∑j kj, where ki is the degree of node i. In this paper, we will set the parameters of BA networks as m0 = m = 2 and N = 1000, where N is the size of the network.
2.2. Attack-cost-based cascading failure model
Previous models of network robustness usually assumed that the attacking cost for any node or link is unified. Actually, due to the heterogeneous practical property of nodes or links, the attack cost of them can be quite different. Following common practices33, we use the degree of nodes to metric the attacking cost of nodes, i.e., ρi = ki, where ρi is the cost to remove node i and ki is the degree of node i. The total attack cost is normalized as:
Previous works have shown that for BA networks the node’s load scales with its degree as 36,37,38:
Next, we will introduce attacking strategies in detail.
Random removal strategy (RRS):
The procedure of RRS is described as follows. At each time step of the strategy, one node is chosen randomly from the unremoved node set of the network.
Low-degree removal strategy (LDRS):
LDRS is described as follows. At each time step a node with the lowest degree in the initial network is chosen from the unremoved node set of the network. If there are two nodes with the same degree, a node will be selected randomly.
High-degree removal strategy (HDRS):
HDRS is a widely used intentional attacking strategy 32. Under HDRS, a node with the highest degree in the initial network is selected at each time step from the unremoved node set of the network. If there are two nodes with the same degree, we randomly chose one node.
Genetic algorithm removal strategy (GARS):
It is known that computational intelligence algorithms can effectively solve many complex optimization problems 8,39,40. Genetic algorithm (GA) is a well-known computational intelligence algorithm41, which was put forward in 1970s. It simulates the evolution procedure in nature and uses the operators for instance selection, crossover and mutation to achieve the enhancement of the fitness value of solutions in population.
Considering the heterogeneous attack cost of nodes and the advantage of GA algorithm, we propose an attack-cost-based attacking strategy named genetic algorithm removal strategy (GARS). In GARS, the length of each chromosome is N, where N is the number of nodes in the network. A node is denoted by a gene and the state of the node is represented by the value of binary bit corresponded to the gene, where 1 denotes the node is removed from the network while 0 denotes the node is alive. We set the crossover probability Pc = 0.95, the population size n = 30 and the maximum generation gm = 100. Here, the uniform mutation is used and the mutation probability Pm = 0.1.
The basic procedure of GA in GARS is described as follows:
Step 1: Set t = 1 and the size of population n = 30. To speed up the optimization speed, we generate one solution (chromosome) by HDRS, one solution by LDRS and randomly generate remainder 28 solutions to compose the first generation population, P1. Evaluating the fitness value of each solution in P1, where the fitness is defined by the value of G after cascading failures.
Step 2: An offspring population Qt is created as follows: (i) Using roulette wheel selection rule, we select two solutions x and y from Pt according to their fitness values. (ii) We use a crossover probability Pc to produce offspring. Calculating the ρ value of each new offspring, if the value of ρ beyond the given total cost value, then randomly select one node and recover its connection state, i.e., change the bit value of the node from 1 to 0. Iterating this procedure until the ρ value of the offspring not large than the given total cost value. Afterwards, we add these offspring to Qt.
Step 3: Every solution x ∈ Qt is uniformly mutated with a given mutation rate Pm.
Step 4: Assign a fitness value to each solution x ∈ Qt according to the value of G corresponded to each solution.
Step 5: Chose n solutions from Qt according to their fitness values and duplicate these solutions to Pt+1.
Step 6: If the maximum generation is reached, return the solution with the highest fitness value in the final population and terminate the algorithm, else, set t = t + 1 and go to Step 2.
In the GARS strategy, the removal nodes are identified by the state of binary bits in the resulting solution of GA.
For above attacking strategies, the removed node set Z is null at the beginning. At each time step a node i is selected by the given attacking strategy and the attacking cost of the node ρi is summed to ρ, i.e., ρ = ρ + ρi. If the ρ value is less than or equal to the given total attacking cost, then node i joins in Z set and node i and its direct links are removed simultaneously, otherwise ρ = ρ − ρi. The iteration is proceeded until ρ equals to the given total attacking cost or we can not find a suitable node to join in the set of Z.
Afterwards, the cascading failure is generated by removing the node u with the highest load in the remained largest connected component. In our model, we adopt the local weighted flow redistribution rule 30, where we tend to allocate more loads to the higher-capacity direct neighbours of failed node to prevent more nodes from overload. Specifically, the loads of the disabled node u, represented by Fu, are distributed to the nearest neighbours of node u. The extra load ΔFj received by the neighbouring node j is defined as:
3. Simulation results and discussion
Firstly, we study the relationship between G and the total attack cost ρ under different attacking strategies (Fig. 1). It is indicate that the value of G decreases as the value of ρ increases, indicating that the network becomes more vulnerable as the total attack cost increases. On the other hand, the value of G under GARS strategy is the lowest, illustrating that the performance of GARS is better than that of other three attacking strategies. Especially, the value of G drops quickly under GARS when the value of ρ is low, which means that in the initial attack phase the performance of GARS can be significantly improved even if we increase a small quantity of attack costs.
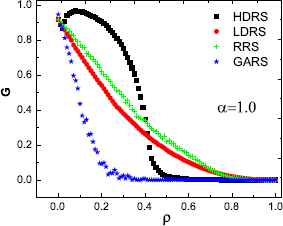
G as a function of the total attack cost ρ under four attacking strategies. Here we set the parameters of BA network N = 1000, m0 = m = 2 and α = 1.0. The results are the average over 100 independent realizations.
Next, we investigate the relationship between G and α with respect to four attacking strategies (Fig. 2(a)). Here we set the total attack cost ρ = 0.2. One can see that under all attacking strategies the value of G increases with the value of α increases, illustrating that the node capacity is of a more safety zone with respect to the node failure as α increases. Furthermore, the value of G under GARS is smaller than that of other strategies, which means that GARS outperforms other attacking strategies.
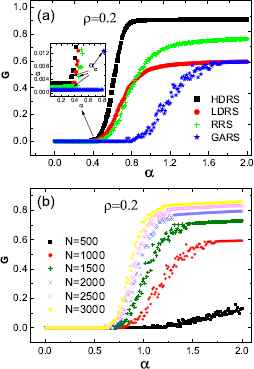
(a) G as a function of the tolerance parameter α under four attacking strategies. The inset shows the critical value αc for different attacking strategies, where network size N = 1000. (b) G versus the tolerance parameter α under GARS for different network sizes (N = 500,1000,1500,2000,2500,3000). Here we set ρ = 0.2 and BA scale-free networks with m0 = m = 2 are used. The results are the average over 100 independent realizations.
The critical value αc is the lowest value of safety capability to prevent networks from global cascades 42,43,44. When α < αc, the giant cluster disappears, reflecting that the global cascading failure emerges. While in the case of α > αc, the global cascade will not emerge. In the inset of Fig. 2(a), we depict the critical value αc under four attacking strategies. This shows that the value of αc with respect to GARS is the highest, showing the weakest network robustness under GARS. To explore the influence of the network size on the critical value αc, we plot the relationship between G and α under GARS with different network sizes (Fig. 2(b)). This indicates that the value of αc decreases as the network size increases, reflecting that under GARS the network robustness increases with its size. Due to the fixed maximum generation of GA in GARS, the larger the network size, the harder it is for GARS to find outstanding nodes for attack.
To explore the effect of total attack cost on the performance of GARS, we plot G versus α with respect to GARS for different total attack costs (ρ = 0,0.2,0.4,0.6,0.8). The results illustrate that the robustness of networks decreases as ρ value increases (Fig. 3), indicating that the total attack cost is of a vital effect on the cascades tolerance of complex networks. When ρ ⩾ 0.6, the relative size of the largest connected cluster G ≈ 0, reflecting that the network is completely disintegrated. In the case of ρ = 0, the value of G ≈ 1 when the value of α is high, which means that the network can be well protected even if GARS attacking strategy is used.
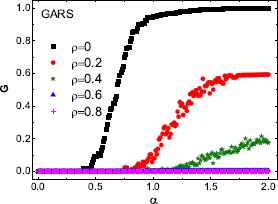
G as a function of α under GARS for different total node attack costs. BA scale-free networks with N = 1000 and m0 = m = 2 are used. The results are the average over 100 independent realizations.
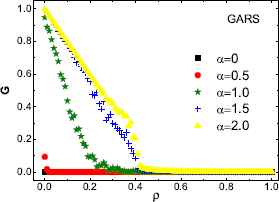
G as a function of the total attack cost ρ under GARS for different tolerance parameters. Here we set N = 1000 and m0 = m = 2. The results are the average over 100 independent realizations.
Finally, we investigate the relation between G and ρ for different values of tolerance parameter (α = 0,0.5,1.0,1.5,2.0). The results show that the network robustness increases as α value increases, meaning that larger tolerance parameters will make networks more stronger to defend cascades even attack cost is taken into account. Besides, in the case of α = 0 and 0.5, the network is quite vulnerable even though the value of ρ is very small (ρ ⩽ 0.05).
4. Conclusion
In this paper, we have proposed an attack-cost-based cascading failure model and compared four attacking strategies, where attack costs correspond to the degree of nodes. The results show that attack costs are of important impacts on the cascades tolerance of networks and the genetic algorithm removal strategy (GARS) can make networks more weaker than other three attacking strategies. We investigate the relationship between the network robustness and tolerance parameter when attack costs are taken into account. It is found that the critical value of tolerance parameter under GARS is much larger than that of other strategies and decreases as the network size increases. We also explore the relationship between the network robustness and attack costs under different values of tolerance parameter. The simulation results indicate that, for low values of tolerance parameter, the network is quite fragile even though the value of total attack cost is very small.
Acknowledgments
The work is supported by the National Natural Science Foundation of China (Grant Nos. 61370138, 61572077), Beijing Municipal Natural Science Foundation (Nos. 4152017, 4162027), Characteristic Subject Research Projects of Beijing Union University (KYDE40201701) and New Starting Point Projects of Beijing Union University (Zk10201602).
References
Cite this article
TY - JOUR AU - Chen Hong AU - Nai-Yu Yin AU - Ning He AU - Oriol Lordan AU - Jose Maria Sallan PY - 2017 DA - 2017/09/14 TI - Cascades Tolerance of Scale-Free Networks with Attack Cost JO - International Journal of Computational Intelligence Systems SP - 1330 EP - 1336 VL - 10 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.10.1.93 DO - 10.2991/ijcis.10.1.93 ID - Hong2017 ER -
