Research on National Pattern Reuse Design and Optimization Method Based on Improved Shape Grammar
- DOI
- 10.2991/ijcis.d.200310.003How to use a DOI?
- Keywords
- Shape grammar; Batik patterns; Optimization design; Pattern reuse; Pattern reuse design system
- Abstract
Considering the low degree of abstraction of traditional shape grammar in national pattern reuse design, this paper proposes a method based on the combination of improved shape grammar and an optimization algorithm to reuse national patterns design. As an application example, we carried out research on the batik pattern elements of the Miao nationality in the “Intangible Cultural Heritage of Guizhou Province” system. Firstly, an improved shape grammar based on synthetic predicate grammar coding is developed to represent the transformation process of design pattern reuse in batik patterns. Then, the number of patterns arranged in a specific position is taken as the optimization variable; the particle swarm optimization algorithm is used to optimize the variables, so as to obtain the optimized predicate shape grammar parameters; and the pattern is reused according to the parameters. A batik design pattern reuse system is also constructed to realize rapid design. The results show that the proposed method can enrich the reuse results of batik pattern elements and realize the rapid design of complex batik patterns.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
National patterns design has an element of fuzziness and uncertainty to them that is related to subjective psychology and image perception [1]. Traditional pattern design is subject to the functional and aesthetic demands of manual design, resulting in low design efficiency and strong subjectivity. However, in recent decades, with the development of computer graphics, machine learning, and the combination of digital and graphic design, computer-aided design (CAD) technology has been able to help designers meet their design requirements [2,3]. Shape grammar, with its grammar rule base, recursive operation mechanism, and intuitive visualization, can explain design well through formal description. In addition, it can creatively support designers to better understand and perceive design and to promote the development of CAD tools, making design more scientific, reliable, and universal [4–6].
In the literature, research on combining shape grammar with other optimization algorithms focuses on combining shape grammar with parallel particle swarm optimization (PSO), which was proposed by Keles [7], in order to solve the problem of embedding and replacing the emergent part after the design is generated with shape grammar. Chau et al. [8] proposed a method that combines shape grammar with lattice theory and uses lattice-based rational quadratic Bézier curves to represent three-dimensional circular arc shape grammar, which solves the complexity of geometric operations related to specific syntactic shapes in shape computation. Jia and Ming [9] proposed the dynamic shape representation based on shape grammar and extent the theory of shape grammar and further enriches the form of grammar rules. To improve traditional shape grammar, Abdelbar and Rachid [10] proposed a parametric shape grammar method to generate a template motif. Jia and Ming [11] proposed hierarchical shape grammar and used descriptive language concepts to apply shape grammar to the creative design of Zhuang embroidery patterns. Zahra et al. [12] proposed the parametric shape grammar design. Although traditional shape grammar has great advantages in design evolution, for the art of graphic design, the degree of abstraction of traditional shape grammar is low. Therefore, for the innovative design of national patterns, the traditional and single use of shape grammar cannot adequately meet the needs of pattern reuse and rapid design.
Therefore, based on the above analysis and considering the problem of low abstraction and reuse of national pattern design, the main contributions of this study are as follows:
An improved shape grammar of comprehensive predicate grammar is developed to represent the generation process of national pattern redesign.
Taking the Miao batik pattern as the application carrier, the number of pattern elements in the pattern is taken as the optimization basis for the first time, the mathematical model is established, and the pattern arrangement parameters are optimized by using the PSO algorithm, so as to obtain the optimized predicate shape grammar parameters and realize the reuse and design generation of pattern elements in the Miao batik pattern. Improved shape grammar is introduced into the design system to realize the rapid design of different patterns.
Pattern elements are obtained that captured high user attention, as demonstrated by an eye movement experiment.
2. RESEARCH BACKGROUND
2.1. Basic Definitions of Shape Grammar
Shape grammar is a common method for pattern design, originally proposed by Stiny and Gips in 1972 [13]. This grammar provides a formal mechanism to support design space exploration by using visual replacement rules and defines shape language by an algorithm, which makes the transformation of shape have the characteristics of label and parameter. The application of shape grammar rules is divided into two steps: (1) sub-shape detection. That is, identifying a specific shape, and (2) replacing it with another shape.
Stiny defined shape grammar as a quadruple, that is,
When there is an Euclidean transformation
By applying the shape rules, new shapes can be continuously generated from the initial shapes, and shape rules are sequentially applied to the obtained shapes; that is, the shape sequence
Based on the abovementioned properties, shape grammar can be regarded as a kind of visualized mathematics. This grammar can abstract the concrete shape into abundant and constructive descriptions, which is convenient for computational implementation and forms the basis of visual computation.
2.2. Euclidean Transformation
Since this study only focuses on the variation of the state model in the two-dimensional space, we only consider Euclidean transformation in the two-dimensional space. That is, Euclidean plane is regarded as a set of points satisfying special relations expressed by distance and angle. A new shape is created by varying the displacement, angle, scale or a limited combination thereof of the initial shapes [14]. The Euclidean distance formula is given in Equation (1):
Figure 1 illustrates the definition of shape grammar and the application of Euclidean transforms in shape grammar.
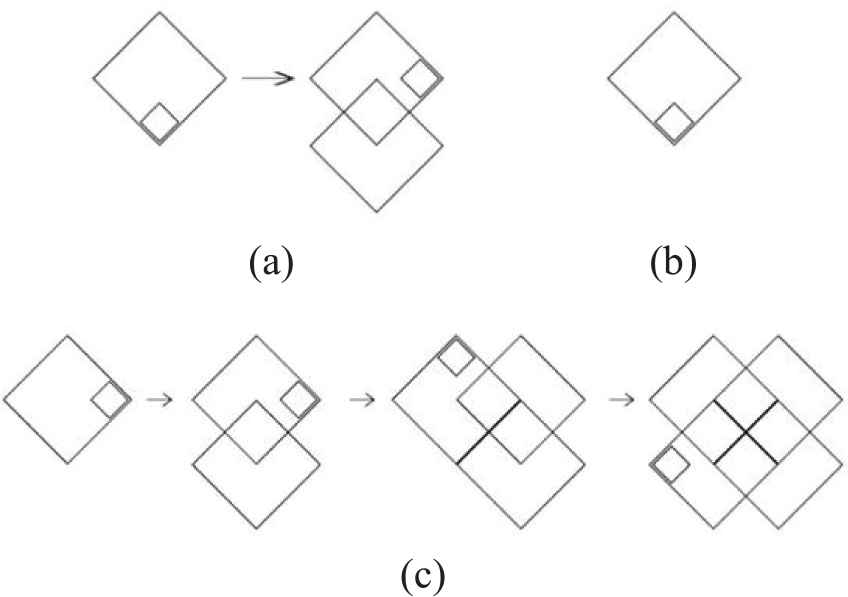
Examples of traditional shape grammar applications. (a) Shape rules; (b) Initial shape; (c) Pattern derivation using shape grammar rules.
The graph generated in Figure 1(c) was derived from the rules of Figure 1(a) and (b). That is, the final graph of Figure 1(c) is obtained by repeatedly applying the rule shown in Figure 1(a), starting from the initial shape shown in Figure 1(b). Each time, the rule uses a different Euclidean transformation to apply a combination of translation and rotation to the left-hand side of the shape rule, with the nested small diamond corresponding to the marker point
2.3. Particle Swarm Optimization
PSO was proposed by Russell Eberhart and James Kennedy in 1995. This algorithm uses a method inspired by the movement of birds or the gathering of fish to optimize a problem. This is accomplished by the direction of individual movement in the population, considering the optimal fitness of the population and its own optimal fitness to achieve the purpose of optimization, and by following the current search for the optimal value to find the global optimum [15,16].
In PSO, the potential solution of each optimization problem is a particle in the search space, each particle has a fitness value determined by an optimized function, and each particle has two main attributes: velocity and position. The position of the particle is a function-specific solution, and the velocity is used to determine the direction of the particle in the next iteration. Therefore, the particle updates itself by tracking two extremes in each iteration: (1) the optimal solution found by the particle itself “individual extremum” and (2) the optimal solution found so far in the entire population “global extremum.”
In a D-dimensional target search space, a colony is composed of N particles, wherein the formula for updating the velocity and the position of the
3. IMPROVED SHAPE GRAMMAR APPLICATION RULES
Traditional shape grammar uses marker points to control the application of shape rules in the design process. Although the sequential programming style can be well used to describe the design process by using marker points, it relies on specific shapes, which makes the design process too rigid [1]. Therefore, this study separate the shape knowledge and transformation process knowledge of patterns, focus on the application of transformation process knowledge; that is, the transformation process
| Predicate | Meaning | Parameters | Range |
|---|---|---|---|
| Tran | Transformation | ||
| Rota | Rotation | ||
| Scal | Scaling | ||
| Circ | Circular | - | |
| Lnar | Line array | - | |
| Mirr | Mirror image | up\down\left\right, 1/0 | - |
| { | start | - | - |
| } | stop | - | - |
Predicate shape grammar encoding table.
In Table 1,
Use
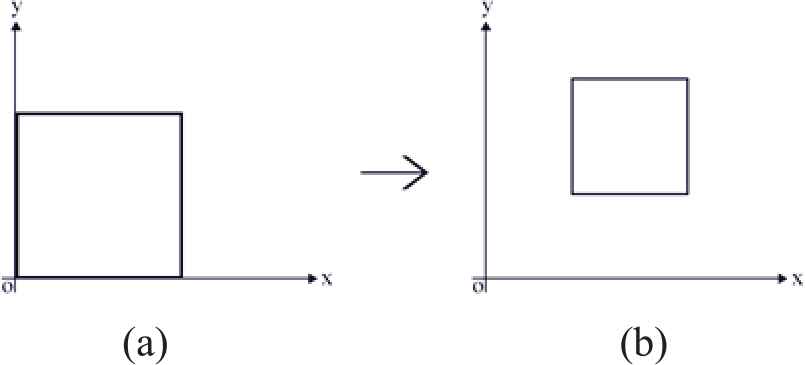
A graphical representation of the basic predicate shape grammar. (a) Initial shape
The basic two-dimensional Euclidean transform matrix is expressed as
The transformation process of Figure 3 is shown in Equation (5):
If there is a circumferential array of shape transformation, that representation is defined as
Since most graphic transformations use transformation
If the initial shape
To eliminate overlap between shapes, define IF IS,
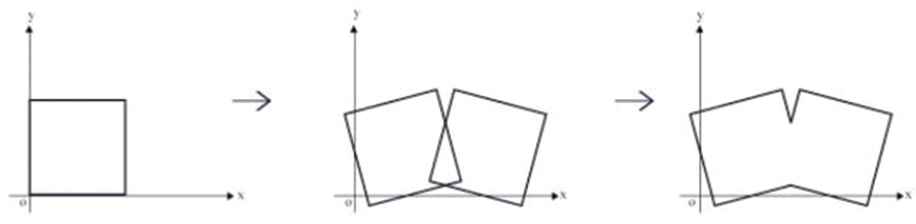
Eliminate overlapping graphic presentations demonstration.
The transformation process of Figure 4 is shown in Equation (7).
If the shape rule is applied to the graph transformed by
Where;
4. APPLICATION EXAMPLE AND OPTIMIZATION DESIGN
Miao batik is mainly distributed in Sichuan, Guizhou, and Yunnan Provinces of China and has a long history. They have numerous design themes and rich patterns, mainly including natural forms such as flowers, leaves, birds, and fish. Batik products include tablecloths, clothing, aprons, cloth bags, and other daily necessities [17].
Taking Miao batik pattern elements as an example, the predicate shape grammar is used to reuse the patterns, and PSO is used to optimize the number of patterns to determine the Euclidean transformation parameters, so as to determine the Euclidean transformation parameters, so that the patterns can be transformed and reused according to the optimized parameters.
4.1. Batik Pattern Extraction
This paper selects the pattern elements of batik from the website of “Intangible Cultural Heritage of Guizhou Province” as the basis of reuse design. Website system as shown in Figure 5.

System home.
Batik patterns are selected from the batik productions example library, as shown in Figure 6.

Batik products. (a) Batik product I; (b) Batik product II; (c) Batik product III.
The pattern element identified by the red box in Figure 6 was selected as the extraction object. When extracting, each pattern element was regarded as a separate closed contour, and the shape context method is used to describe and match the pattern elements [18,19]. The Canny operator [20] is also used to obtain the contour of the shape of the pattern by sampling to obtain the contour sampling points, and then plane software was used to modify the extracted patterns. The results are shown in Figure 7.

Pattern matching and extraction results. (a) Patterns extracted from batik product I; (b) Patterns extracted from batik product II; (c) Patterns extracted from batik product III.
4.2. Application of Improved Shape Grammar
Batik patterns include the main, corner, and border pattern elements [21], with special attention to the pattern element arrangement symmetry, single pattern irregularity, and the overall spatial arrangement of strong features. Based on these characteristics, it is feasible to characterize the reuse process of pattern elements with improved shape grammar.
Taking the pattern elements are shown in Figure 7(a) and (b) as examples for reuse design. The Figure 7(a) pattern element is set as
Similarly, the reused graphics can be added or deleted as required by the design, as shown in Figure 8(c). If the final patterns shown in Figure 8(c) and (d) are subjected to linear array rule processing and then to combination processing, the two patterns can be reused to design articles such as simple tablecloths or wall decorations, as shown in Figure 9.
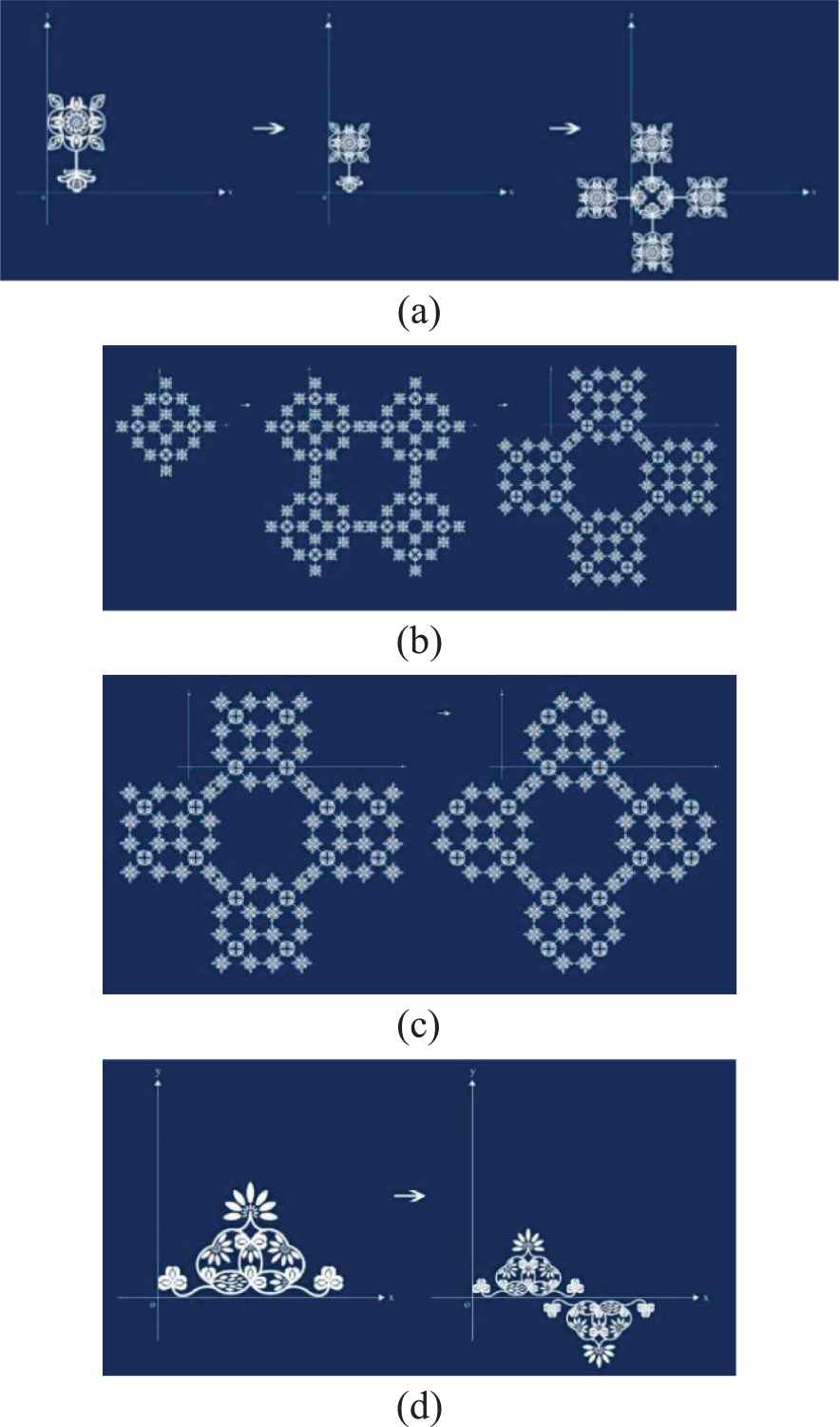
Predicate shape grammar instance application. (a) Pattern formed according to

Reuse design result.
4.3. Application of Optimization Algorithm
According to the type of batik pattern and the characteristics of the pattern elements in Figure 7(a)–(c), the pattern of Figure 7(a) is used as the main pattern, and Figure 7(b) and (c) are used as the border element pattern. As shown in Figure 10, the circular configuration mode of the batik pattern is selected. The corresponding position is selected according to the different functions of each pattern, and corner elements are not arranged for circular configuration.
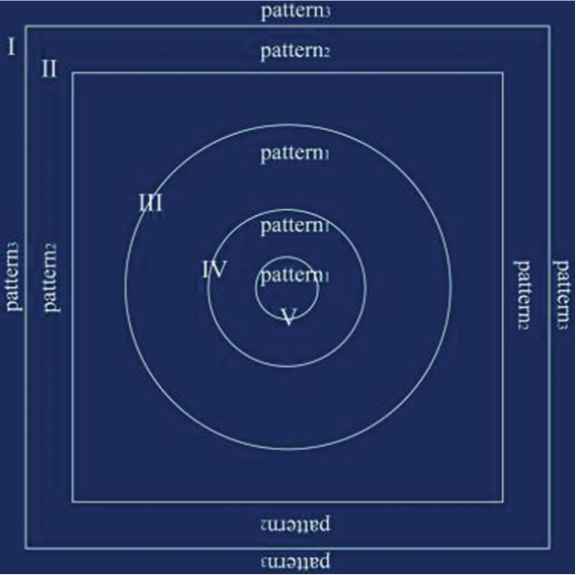
Configuration and regionalization.
When Figure 7(a) (
When Figure 6(b) and (c) are used as border pattern elements, two transformation modes were defined, as shown in Equations (12–14), respectively:
4.3.1. Mathematical model construction
In this study, the PSO algorithm is used to optimize the number of layouts of each pattern at a specified position. First, according to the size parameters shown in Figure 11, the overall mathematical model is established, as shown in Equation (15):
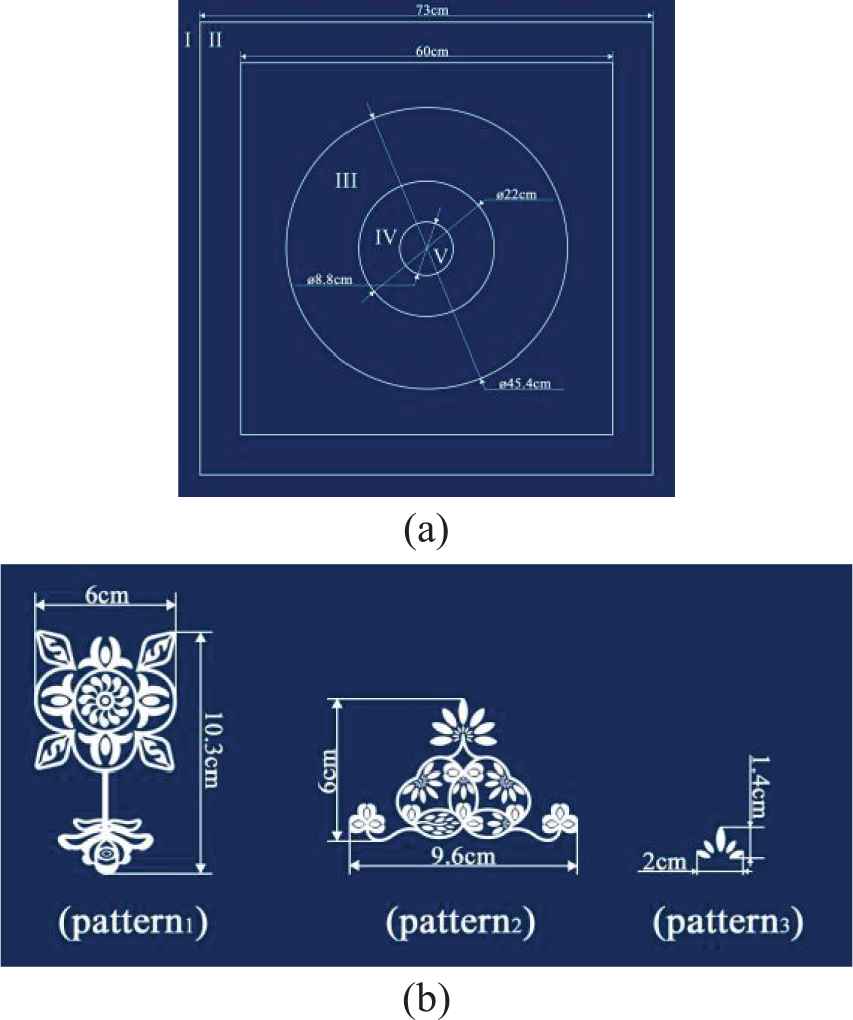
Dimensional parameters. (a) Each frame size parameters; (b) Initial size parameters of each patterns.
Where;
According to the placement position of each pattern in Figure 11 and the size parameters of each part in Figure 11, a mathematical model was established according to the transformation mode of Equations (10) and (12–14) as the basis of reuse transformation, as shown in Equation (16):
Where;
4.3.2. Result analysis
MATLAB R2017 software is used as the optimization tool, the local and global acceleration constants of the PSO were set as
| Variable | |||||
|---|---|---|---|---|---|
| Number of Groups | |||||
| Group 1 | 20.431 | 5.181 | 22.288 | 7.360 | 2.060 |
| Group 2 | 33.271 | 6.269 | 18.184 | 7.216 | 4.425 |
| Group 3 | 26.166 | 4.235 | 13.233 | 11.985 | 3.063 |
| Group 4 | 15.326 | 5.236 | 16.459 | 9.425 | 4.383 |
| Group 5 | 18.415 | 6.806 | 23.775 | 6.347 | 4.977 |
Selecting five sets of PSO data optimized according to Equation (16).
Since
The first set of optimized data was combined with the predicate shape grammar vocabulary

Pattern element reuse design result I. (a) Group 1 data pattern; (b) Group 2 data pattern; (c) Group 3 data pattern; (d) Group 4 data pattern; (e) Group 5 data pattern.
If the pattern formed by the transformation rule of Equation (11) is used as the main element, the constraints

Pattern element reuse design result II. (a) Group 1 data pattern; (b) Group 2 data pattern; (c) Group 3 data pattern; (d) Group 4 data pattern; (e) Group 5 data pattern.
| Variable | |||||
|---|---|---|---|---|---|
| Number of Groups | |||||
| Group 1 | 19.785 | 4.881 | 9.713 | 4.231 | 1.985 |
| Group 2 | 32.871 | 6.417 | 6.845 | 5.437 | 1.667 |
| Group 3 | 26.166 | 4.235 | 8.143 | 3.415 | 2.015 |
| Group 4 | 15.326 | 5.236 | 11.306 | 5.843 | 1.788 |
| Group 5 | 17.935 | 6.746 | 9.451 | 3.472 | 2.855 |
Selecting five sets of PSO data optimized according to Equation (18).
As seen from that above reuse results, the same transformation rules were applied to the body patterns in Figures 12 and 13, respectively. However, for the border pattern
4.4. Construction of Pattern Reuse Design System
In order to apply the predefined improved shape grammar to the reconfiguration design of different pattern frames quickly, the predicate shape grammar expression is applied to the process implementation, and the batik pattern reuse design system is constructed to achieve the rapid pattern frame reuse design. The system implementation is shown in Figure 14.
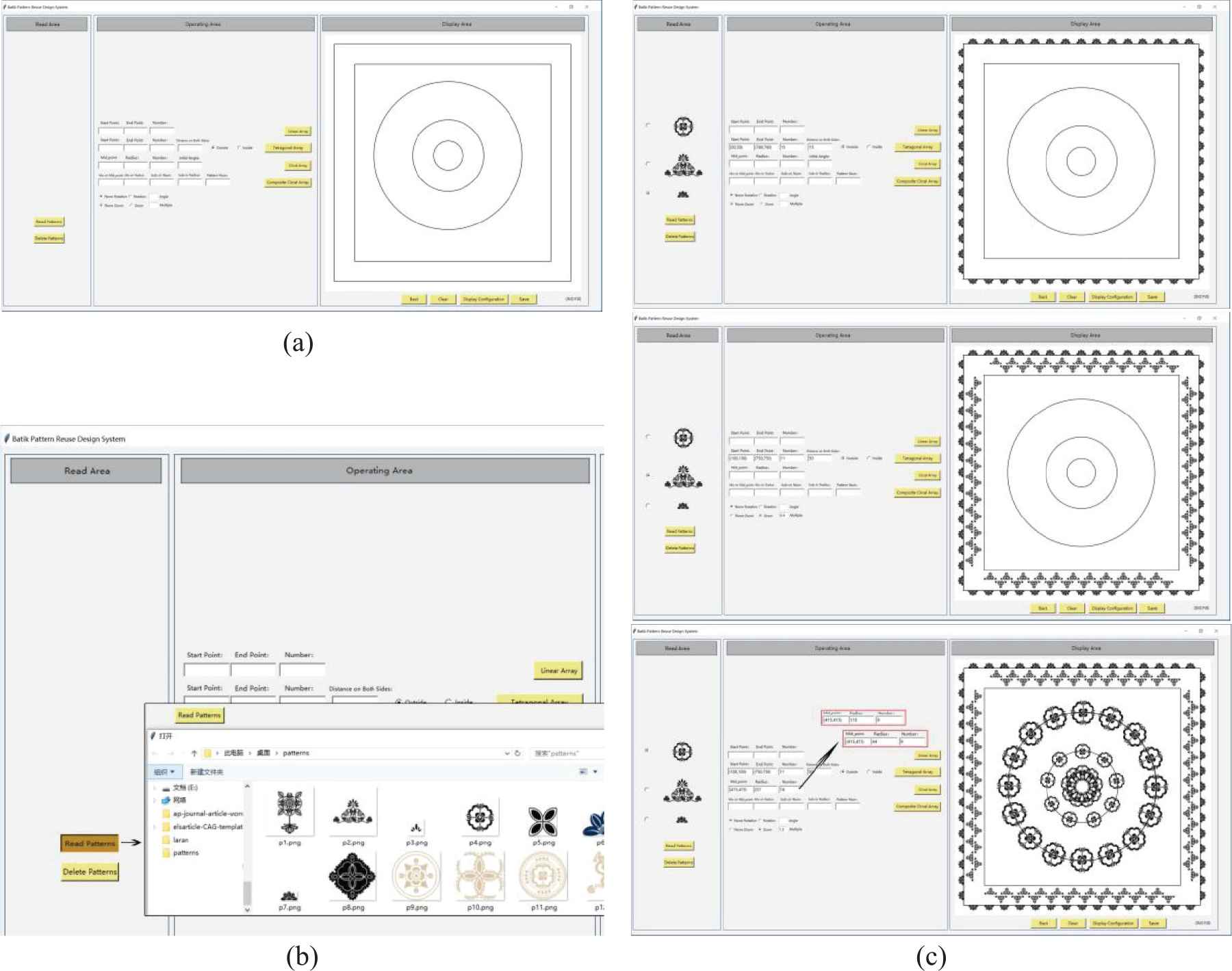
System design. (a) Initial interface; (b) Reading batik patterns; (c) Apply rules to generate patterns.
The system is divided into three main areas: read, operation, and display. The reading area is used to display the pattern elements to be arranged, the operation area is used to input relevant parameters to arrange the pattern elements, and the display area is used to display the results of the operation. The system can obtain the coordinates of the corresponding position by clicking the mouse on the canvas of the display area.
5. EXPERIMENTAL COMPARISON AND RESULT ANALYSIS
In this study, the Eyeso eye tracker is used to perform eye movement experiments [22,23] on 10 patterns based on the PSO-optimized data reuse design. Twenty postgraduates are selected and their uncorrected or corrected visual acuity is above 1.0. The subjects were required to sit 0.5 m in front of the screen and adjust the angle of the eye mover to 15°, as shown in Figure 15.

Eye movement experiment scene.
In the experiment, 10 patterns are arranged out of order into three groups to counteract the influence of the different display position of each pattern on the experimental results. The sample code and arrangement of the experimental group are shown in Figure 16. The experiment measured the fixation time of the subjects on different patterns and calculated the average fixation time of each pattern, as well as the hot spot map of the longest fixation pattern. The experimental results are shown in Figure 17.

Sample coding and disordered arrangement of the experimental group. (a) Sample coding; (b) Group 1; (c) Group 2; (d) Group 3.
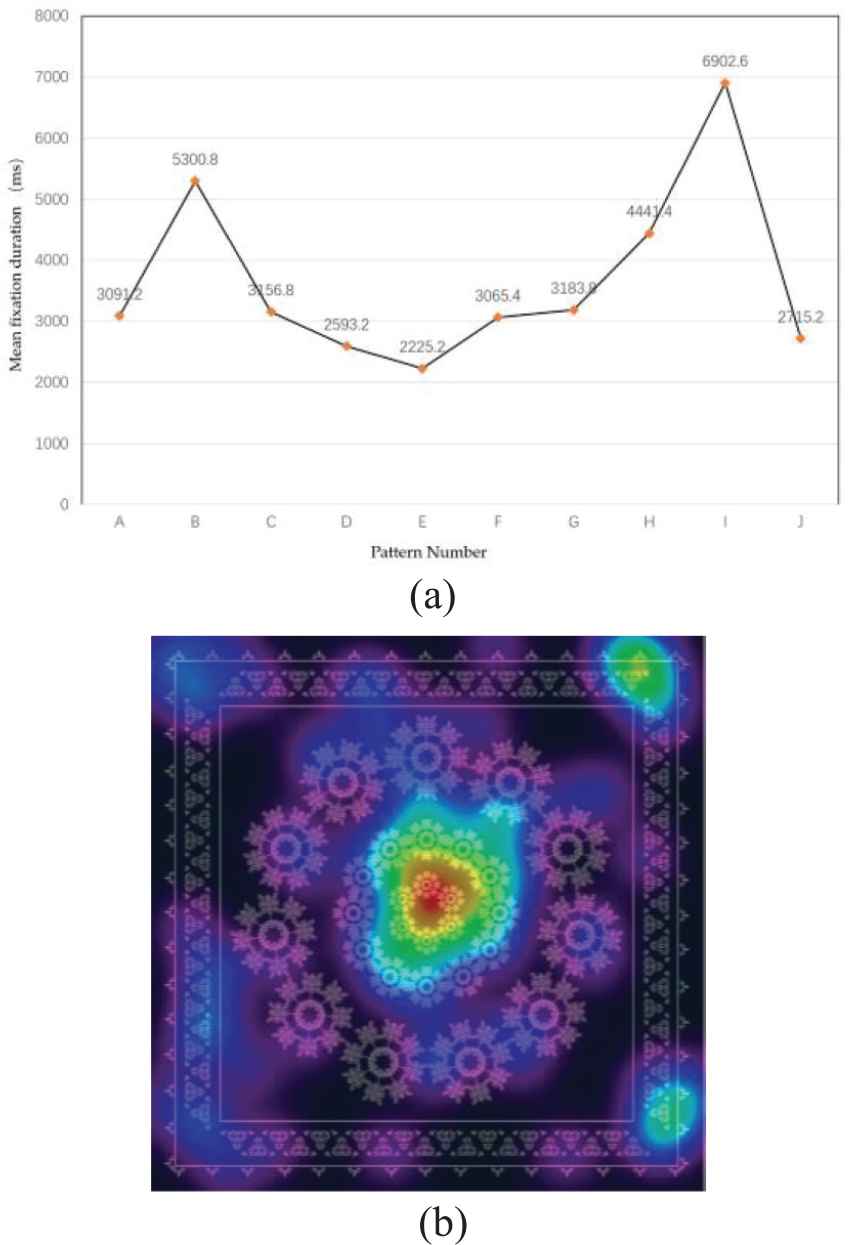
Eye movement test results. (a) Mean fixation time comparison chart; (b) The hotspot map for the longest gaze pattern.
The results showed that the mean fixation time of different patterns is in the order of I > B > H > G > C > A > F > J > D. Thus, the subjects pay more attention to the patterns formed from the fourth group of data in Table 3, and the hot spot map shows that the subjects pay more attention to the main pattern elements than the border elements.
The A–E encoded pattern (i.e., the subject pattern formed by the transformation rule of Equation (10)) had a total fixation duration average of 16,357.2 ms. The F–J encoded pattern (i.e., the subject pattern formed by the transformation rule of Equation (11)) had a mean total fixation duration of 20,308.4 ms, indicating that the subjects were more interested in the subject pattern formed by the transformation rule of Equation (11).
6. CONCLUSION AND PERSPECTIVES
Aiming at the problem of the low abstraction degree of traditional shape grammar in design pattern reuse, the concept of predicate shape grammar vocabulary is proposed to represent the concrete process of pattern reuse design, which transfers the traditional shape grammar from the initial shape to a transformation process and enhances the abstraction of the shape grammar.
The improved shape grammar is applied to the reuse design of Miao batik pattern elements. The results show that the improved shape grammar can satisfy the reuse design of batik pattern elements. It is the first time that improved shape grammar and PSO have been combined to form multiple batik patterns, which proves the good scalability of the method.
Through eye movement experiments, it is concluded that the subjects are more interested in the main pattern elements formed by the transformation rules of Equation (11), which shows that complex patterns and compact arrangement can attract people's attention. As for the main pattern formed by the transformation rules of Equations (10) and (11), the pattern formed by the fourth group of data in Table 3 is more noticeable to the subjects according to the second group of Table 2. According to the hot spot map, the subjects pay more attention to the main pattern. Therefore, in the future work, the design emphasis should be placed on the design and coding of the main pattern elements.
Future work will focus on deepening the content of Section 4.4, that is, expanding the function of the system for pattern reuse design and improving the flexibility and accuracy of pattern reuse design.
CONFLICT OF INTEREST
The authors declare no conflicts of interest.
AUTHORS' CONTRIBUTIONS
Supervision, N.D.; conceptualization, N.D. and J.L.; research methodology, N.D. and L.H.; experimental operation, N.D. and L.H.; writing—review and editing, N.D. supervision, J.L.; project administration, J.L.
Funding Statement
This research was supported by the Natural Science Foundation of China (Nos. 51865004, 2014BAH05F01) and the Provincial Project Foundation of Guizhou, China (Nos. [2018]1049, [2016]7467).
ACKNOWLEDGMENTS
The authors thank the anonymous reviewers for their valuable suggestions and important comments which greatly helped them to improve the presentation of this manuscript.
REFERENCES
Cite this article
TY - JOUR AU - Ning Ding AU - Jian Lv AU - Lai Hu PY - 2020 DA - 2020/03/17 TI - Research on National Pattern Reuse Design and Optimization Method Based on Improved Shape Grammar JO - International Journal of Computational Intelligence Systems SP - 300 EP - 309 VL - 13 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.200310.003 DO - 10.2991/ijcis.d.200310.003 ID - Ding2020 ER -
