Hierarchical Bayesian Choice of Laplacian ARMA Models Based on Reversible Jump MCMC Computation
- DOI
- 10.2991/ijcis.d.200310.006How to use a DOI?
- Keywords
- ARMA time series; Hierarchical Bayesian; Laplacian noise; Reversible jump MCMC
- Abstract
An autoregressive moving average (ARMA) is a time series model that is applied in everyday life for pattern recognition and forecasting. The ARMA model contains a noise which is assumed to have a specific distribution. The noise is often considered to have a Gaussian distribution. However in applications, the noise is sometimes found that does not have a Gaussian distribution. The first objective is to develop the ARMA model in which noise has a Laplacian distribution. The second objective is to estimate the parameters of the ARMA model. The ARMA model parameters include ARMA model orders, ARMA model coefficients, and noise variance. The parameter estimation of the ARMA model is carried out in the Bayesian framework. In the Bayesian framework, the ARMA model parameters are treated as a variable that has a prior distribution. The prior distribution for the ARMA model parameters is combined with the likelihood function for the data to get the posterior distribution for the parameter. The posterior distribution for parameters has a complex form so that the Bayes estimator cannot be determined analytically. The reversible jump Markov chain Monte Carlo (MCMC) algorithm was adopted to determine the Bayes estimator. The first result, the ARMA model can be developed by assuming Laplacian distribution noise. The second result, the performance of the algorithm was tested using simulation studies. The simulation shows that the reversible jump MCMC algorithm can estimate the parameters of the ARMA model correctly.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
An autoregressive moving average (ARMA) is a time series model that is applied to modeling and forecasting in various fields, for example, [1–3]. The ARMA model is used in the field of short-term load system for forecasting [1]. The ARMA model is used in the field of science for forecasting wind speed [2]. The ARMA model is used in the business field for modeling volatility and risk of shares financial markets [3].
This ARMA model contains a noise. This noise is assumed to have a specific distribution. Noise for ARMA models is often considered to have a Gaussian distribution, for example, [4–7]. The ARMA model is used for sequential and non-sequential acceptance sampling [4]. The ARMA model is used to investigate the non-residual residual surges [5]. The ARMA model is used to predict small-scale solar radiation [6]. The ARMA model is used to forecast passenger service charge [7]. In an ARMA model application, the noise sometimes shows that it does not have a Gaussian distribution. Several studies related to ARMA models with non-Gaussian noise can be found in [1–3,8,9]. Estimating ARMA parameters with non-Gaussian noise is investigated using high-order moments [8]. A cumulant-based order determination of ARMA models with Gaussian noise is studied in [9].
A Laplacian is a noise investigated by several authors, for example, [10–12]. If x is a random variable with a Laplace distribution then
Here,
If the ARMA model is compared to the AR model and the MA model, the ARMA model is a more general model than the AR model and the MA model. If the ARMA model is compared to the ARIMA model, the only difference is the integrated part. Integrated refers to how many times it takes to differentiate a series to achieve stationary condition. The ARMA model is equivalent to the ARIMA model of the same MA and AR orders with no differencing. An ARMA model was chosen instead of the other models such as AR model, MA model, or ARIMA model because the ARMA model can describe a more general class of processes than AR model and MA model. The ARMA model in this study has stationary and invertible properties that are not possessed by the ARIMA model.
This paper consists of several parts. The first part gives an introduction regarding the ARMA model and its application. The second part explains the method used to estimate the ARMA model. The third part presents the results of the research and discussion. The fourth section gives some conclusions and implications.
2. MATERIALS AND METHODS
This paper uses an ARMA model that has Laplacian noise. The parameters used in ARMA model are the order of the ARMA model, the coefficients of the ARMA model, and the variance of the noise. The parameter estimation of the ARMA model is carried out in the Bayesian framework. The first step determines the likelihood function for data. The second step determines the prior distribution for the ARMA model parameters. The reason about the consideration of prior distribution is to improve the quality of parameter estimation. The prior distribution can be determined from previous experiments. The Binomial distribution is chosen as the prior distribution for ARMA orders. The uniform distribution is selected as the prior distribution for the ARMA model coefficient. The inverse Gamma distribution is selected as the prior distribution for the noise parameter. The third step combines the likelihood function for data with the prior distribution to get the posterior distribution. The fourth step determines the Bayes estimator based on the posterior distribution using the reversible jump Markov chain Monte Carlo (MCMC) algorithm [13]. Time series modeling via reversible jump MCMC is a very well studied topic in the literature [14,15]. The power of reversible jump MCMC algorithm is in the fact that it can move between space of varying dimension and not that it is just a simple MCMC method. The fifth step tests the performance of the reversible jump MCMC algorithm by using simulation studies.
3. RESULTS AND DISCUSSION
This section discusses the likelihood function for data, Bayesian approach, reversible jump MCMC algorithm, and simulations.
3.1. Likelihood Function
Suppose that
The values of
With a variable transformation between
Suppose that
The
The
In the probability function for this data,
3.2. Prior and Posterior Distributions
The Binomial distribution with the parameter
The prior distribution for
The prior distribution for
The inverse Gamma distribution with parameter
For
This prior distribution contains a parameter, namely:
Finally, the Jeffreys distribution is chosen as the prior distribution for
By using the Bayes theorem, distribution posterior for
This posterior distribution has a complex form so that the Bayes estimator cannot be determined explicitly. The reversible jump MCMC algorithm was adopted to determine the Bayes estimator.
3.3. Reversible Jump MCMC
The basic idea of the MCMC algorithm is to treat the parameters
Distribution for
The distribution for
3.4. Birth of the Order p
Suppose that
The ratio for likelihood function can be stated by
The ratio between the prior distribution for order
The ratio between posterior distribution for order
While the ratio between the distribution of
If
3.5. Death of the Order p + 1
Death of the order
In contrast, the old Markov chain will remain with the probability
3.6. Change of the Coefficient r ( p )
Let
In this change in coefficient, the likelihood function ratio can be written by
While the ratio between the distribution of
3.7. Birth of the Order q
Let
The ratio for the likelihood function can be stated by
The ratio between the prior distribution for order
The ratio between posterior distribution for order
While the value of the ratio between the distribution of
If
3.8. Death of the Order q + 1
The death of order
In contrast, the old Markov chain will remain with the probability
3.9. Change of the Coefficient ρ ( q )
Let
In this change in coefficient, the ratio for the likelihood function can be written by
While the ratio between the distribution of
4. SIMULATIONS
The performance of the reversible jump MCMC algorithm is tested using simulation studies. The basic idea of simulation studies is to make a synthesis time series with a predetermined parameter. Then the reversible jump MCMC algorithm is implemented in this synthesis time series to estimate the parameter. Furthermore, the value of the estimation of this parameter is compared with the value of the actual parameter. The reversible jump MCMC algorithm is said to perform well if the parameter estimation value approaches the actual parameter value.
4.1. First Simulation
One-synthetic time series is made using Equation (2). The length of this time series is 250. The parameters of the ARMA model are presented in Table 1.
| (2, 3) | 1 |
The parameter value for synthetic ARMA (2, 3).
Synthetic time series data with ARMA (2, 3) model are presented in Figure 1. This synthetic time series contains noise that has a Laplace distribution.
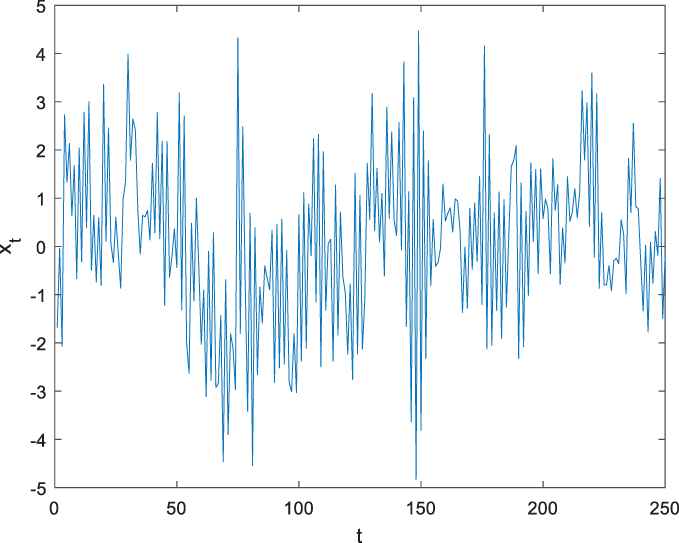
Synthetic time series with ARMA (2, 3) model.
This synthetic time series is used as input for the reversible jump MCMC algorithm. The algorithm runs as many as 100,000 iterations with a 25,000 burn-in period. The output of the reversible jump MCMC algorithm is a parameter estimation for the synthetic time series model. The histogram of order p for the synthetic ARMA model is presented in Figure 2.
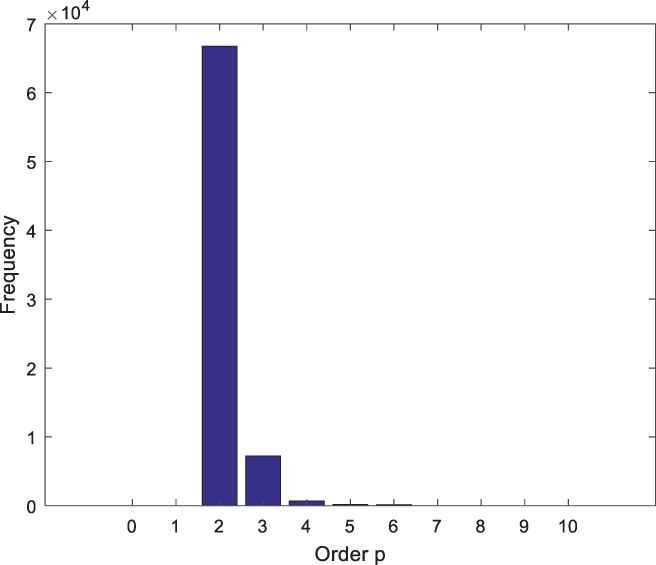
Histogram for order p of the synthetic ARMA (2, 3) model.
Figure 2 shows that the maximum order of p is reached at value 2. This histogram shows that the order estimate for p is

Histogram for order q of the synthetic ARMA (2, 3) model.
Figure 3 shows that the maximal order of q is reached at value 3. This histogram shows that the order estimation for q is
| (2, 3) | 1.0058 |
Estimation of the parameter for the ARMA (2, 3) model.
If Table 2 is compared with Table 1, the parameter estimation of the ARMA model approaches the actual parameter value.
4.2. Second Simulation
Other one-synthetic time series is made using Equation (2). The length of this time series is also 250, but the parameters are different. The parameters of the ARMA model are presented in Table 3
| (4, 2) | 1 |
The parameter value for synthetic ARMA (4, 2).
In this second simulation, the parameters of synthetic ARMA model are taken differently. Synthetic ARMA (4, 2) time series data are presented in Figure 4. This synthetic time series data contains noise that also has a Laplace distribution.
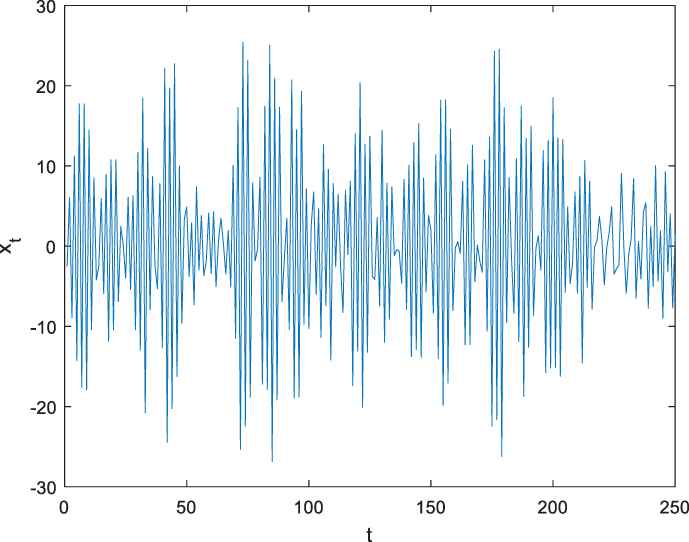
Synthetic time series with ARMA (4, 2) model.
This synthetic time series is used as input for the reversible jump MCMC algorithm. The algorithm runs as many as 100,000 iterations with a 25,000 burn-in period. The output of the reversible jump MCMC algorithm is a parameter estimation for the synthetic time series model. The histogram of order p for the synthetic ARMA model is presented in Figure 5.
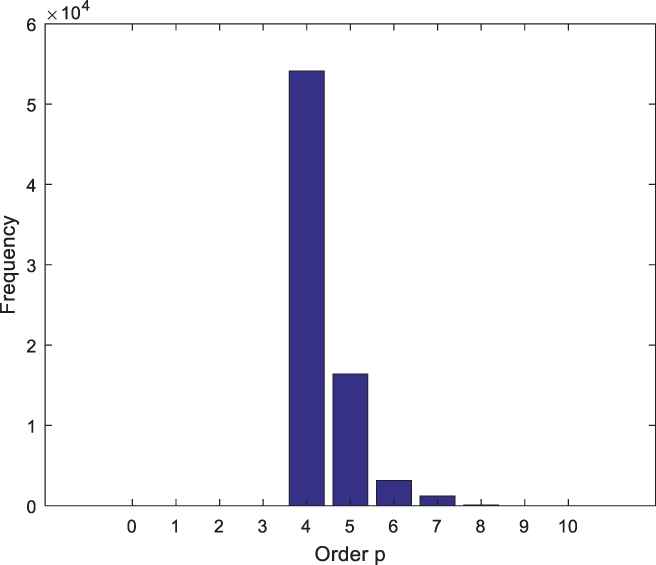
Histogram for order p of the synthetic ARMA (4, 2) model.
Figure 5 shows that the maximum order of p is reached at 4. This histogram shows that the order estimate for p is
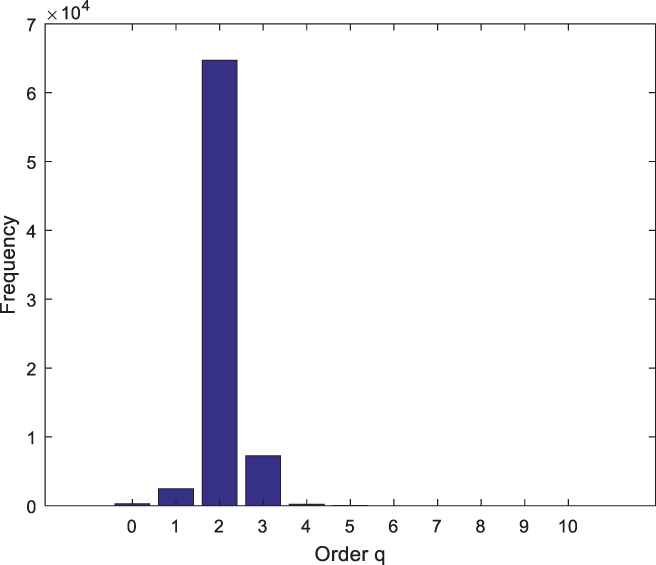
Histogram for order q of the synthetic ARMA (4, 2) model.
Figure 6 shows that the maximal order of q is reached at value 2. This histogram shows that the order estimation for q is
| (4, 2) | 1.1015 |
Estimation of the parameter for the ARMA (4, 2) model.
If Table 4 is compared with Table 3, the parameter estimation of the ARMA model approaches the actual parameter value. The first simulation and the second simulation show that the reversible jump MCMC algorithm can estimate the parameter of the ARMA model correctly.
If the underlying model is wrong will produce a biased estimator. So that the ARMA model is not suitable for modeling data. There is a way to identify whether the wrong model is chosen in the following way. The model is used to predict
5. CONCLUSION
This paper is an effort to develop a stationary and invertible ARMA model by assuming that noise has a Laplacian distribution. The ARMA model can be used to describe future behavior only if the ARMA model is stationary. The ARMA can be used to forecast the future values of the dependent variable only if the ARMA model is invertible. Identification of ARMA model orders, estimation of ARMA model coefficients, and estimation of noise variance carried out simultaneously in the Bayesian framework. The Bayes estimator is determined using the MCMC reversible jump algorithm. The performance of reversible jump MCMC is validated in the simulations. The simulation shows that the reversible jump MCMC algorithm can estimate the parameters of the ARMA model correctly.
ACKNOWLEDGMENTS
The author would like to thank to the Ahmad Dahlan University (Indonesia) in providing grant to publish this paper. Also, the author would like to thank the reviewers who commented on improving the quality of this paper. Not to forget, the author would like to thank Professor A. Salhi, Essex University (UK).
REFERENCES
Cite this article
TY - JOUR AU - Suparman PY - 2020 DA - 2020/03/18 TI - Hierarchical Bayesian Choice of Laplacian ARMA Models Based on Reversible Jump MCMC Computation JO - International Journal of Computational Intelligence Systems SP - 310 EP - 317 VL - 13 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.200310.006 DO - 10.2991/ijcis.d.200310.006 ID - 2020 ER -
