Applying Heuristic Algorithms to Solve Inter-hospital Hierarchical Allocation and Scheduling Problems of Medical Staff
- DOI
- 10.2991/ijcis.d.200310.004How to use a DOI?
- Keywords
- Heuristic algorithms; Staff allocation; Staff scheduling; Inter-hospital; Particle swarm optimization
- Abstract
To address the inter-hospital hierarchical allocation and scheduling problems, this research used the pooling resource concept to allocate medical staff among hospital branches as well as determine their monthly schedules. This study proposed a two-stage strategy. The first stage proposed three heuristic algorithms—HRA1 (human resource allocation based on the hospital's size), HRA2 (human resource allocation based on the average allocation), and HRA3 (human resource allocation based on the severity of penalties)—for medical staff allocation. The second stage used the improved particle swarm optimization (PSO) algorithm to schedule the medical staff within a reasonable time. Based on the numerical results, HRA3 was superior to HRA1 and HRA2. Furthermore, the analysis of two scenarios—varying the sizes of hospital branches (Scenario 1) and varying the total number of medical staff (Scenario 2)—showed that, when the sizes of hospital branches varied (Scenario 1), HRA3 was superior to HRA1 and HRA2 whereas, when the sizes were given (Scenario 2), the lowest number of medical staff possible was approximately 60. The findings of this research will help hospital managers make decisions concerning the allocation and scheduling of medical staff.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
The appropriate management of medical staff has always been one of the most crucial topics for hospital managers [1–5]. Medical staff can influence the quality of medical care directly because they have the most direct contact with patients [6–9]. Consequently, whether medical staff can properly use their time on the job and whether managers can effectively allocate medical staff are critical factors that influence the quality of healthcare for patients [10].
The allocation of medical staff is a personnel management method used to effectively allocate sufficient, capable medical personnel to satisfy the needs of the hospital or medical institution. An effective and efficient system for allocating and scheduling medical staff must be developed to create schedules that satisfy patients' needs and save time and effort expended by the medical staff [2,11–18]. In recent years, research into the problems associated with the allocation of medical staff has focused on allocation within the individual department or hospital and on allocations among inter-departments or inter-organizations [12,14,19,20]. The appropriate allocation of medical staff reduces the waste of medical resources and alleviates the shortage of medical staff in certain hospitals by providing additional medical personnel.
The inter-hospital allocation of medical staff can increase the flexibility of the schedules of medical personnel, satisfy individual scheduling requirements, and enhance the quality of healthcare for patients [11]. In inter-hospital collaboration, some hospitals/branches are located in rural areas while others are located in urban areas. Based on these geographic locations and demographic populations, the scale (such as the number of beds, medical staff, and medical resources) of hospitals is different as is the number of patients. For hospitals located in rural areas, it is sometimes difficult to recruit enough medical staff to serve patients. Decisions related to recruiting sufficient medical staff for hospitals located in rural areas are critical for hospital managers. One possible way to overcome this problem is for hospitals located in urban areas to sign contracts with their medical staff by increasing their salaries or providing certain incentives in order to rotate medical staff to different working places. If inter-hospital managers can work and communicate with each other to deal with medical staff allocation problems, a rotation or supporting plan among hospitals/branches will be a better and more practical way to resolve human-resource shortage problems. Therefore, the inter-hospital managers should periodically review their future patients' demands, and then reallocate inter-hospital medical staff in order to satisfy patients' demands. This is the main practical motivation for the researchers to conduct this research.
Based on the literature reviewed, only a few researchers have studied the inter-hospital allocation and scheduling of medical staff [11,21]. Having a sufficient number of medical staff scheduled and providing a reasonable schedule for their work are important to medical personnel, resulting in reductions in the number of dissatisfied medical staff and fewer complaints. Therefore, it is essential to design and implement an inter-hospital allocation and scheduling system for medical staff that effectively and flexibly allocates sufficient medical personnel to each hospital.
Scheduling the medical staff (i.e., the nurse scheduling issue) is a highly complex, non-deterministic polynomial-time hard (NP-hard) problem [22]. Most previous studies examining the issue of scheduling medical staff have focused on the scheduling of known quantities of medical staff. Hence, the purpose of the current research was to determine inter-hospital allocations and schedules for medical staff according to the restrictions and requirements of each hospital to reduce the dissatisfaction of medical personnel with their schedules. In this study, we developed three heuristic algorithms embedded with the improved particle swarm optimization (PSO) algorithm [23] to solve the inter-hospital, hierarchical problems of allocating and scheduling medical staff. We accessed the radiology departments in three branches of a hospital to collect information concerning the allocation and scheduling of radiologists at these three facilities. We used C++ programming to construct the proposed methodology for the allocation and scheduling of radiologists in the three facilities and subsequently investigated the radiologists' perceptions concerning how well the individual schedules performed. The research results can help decision makers save a large amount of time and effort in the allocation and scheduling of medical staff members, thereby enhancing the job satisfaction of the medical personnel and enhancing the quality of service provided by hospitals and medical institutions.
The rest of this article is organized as follows. In Section 2, we review the literature on the allocation and scheduling of medical staff. Section 3 describes the proposed methodology, presents the mathematical model that was developed, and describes the three heuristic algorithms that were developed and embedded with the improved PSO algorithm. In Section 4, a case study of three branches of the hospital is used to illustrate the procedures of the proposed methodology, including the analysis of two scenarios and a summary of the managerial implications. Finally, Section 5 provides our conclusions and presents our suggestions for future research directions.
2. LITERATURE REVIEW
2.1. Allocation of Medical Staff
The allocation of manpower allocation, also called human resource planning, is a critical social resource. Byars and Rue [24] stated that human resource planning represents the largest investment of an organization; therefore, the management design for human resources is a management measure for supporting and coordinating the various operations of organizational human resources. The allocation of medical staff in a hospital refers to “the process used to determine and deploy the acceptable number and skill mix of personnel needed to meet the care needs of patients” [25]. Inappropriate allocations of medical staff easily can result in disadvantages, such as wastes of human resources and reduced quality of medical care. The estimation of the supply and demand of medical staff is currently the most critical topic in the allocation of medical staff, and hospital management is affected significantly by government and hospital policies. Therefore, it is crucially important for hospitals to allocate suitable numbers of medical staff to fulfill patients' needs and expectations, to manage clinical practices (nurse-to-patient ratios), and to achieve satisfactory operational performance [7,18,26].
Tsay and Wang [27] indicated that the allocation of medical staff does not simply involve quantity. Other factors that influence the supply and demand of medical staff of a hospital include workloads, the work environment, complexity, skill levels, cooperation among the nursing staff, and cost efficiency of nursing care. Consequently, allocating medical staff to each hospital in a network and fulfilling the characteristics and requirements of individual schedules is a crucial topic for hospital management to establish an optimal model for effective allocation of medical staff.
According to reference [28], the prolonged average life expectancy in developing countries has increased uses and costs of medical services. Their study proposed a backtracking approach for constraint satisfaction problems, which were allocation problems of medical staff. They provided optimal allocation plans of medical staff for reducing the hospital's personnel cost.
Shahnazari-Shahrezaei [19] studied an allocation problem of staff, which contained the number of employees, specialization of employees, and skill levels of employees. According to the shift requirements and employees' preferences, they used the fuzzy goal programming model to determine the number of employees each shift and the employees' four-week schedules. The results showed that the proposed method could provide useful solutions for hospital managers to make decisions between two objectives, that is, the satisfaction level of the employers' objectives and the employees' preferences.
Wright and Mahar [11] considered a multi-hospital and cross-department allocation and scheduling problems of medical staff. They applied the pooling (or centralized) concept to construct the proposed problem and used CPLEX software to obtain the optimal solution. The results showed that the proposed method could significantly improve the satisfaction of nurses, reduce overtime, and decrease total cost.
Bouajaja and Dridi [17] surveyed existing literatures on human resource allocation problem (HRAP) in terms of methods such as exact, heuristics, and meta-heuristics and its real-life applications in various fields: production planning, maintenance management, hospital systems, project management, and so on.
Fugener [29] examined the nurse scheduling problem from the perspectives of mid-term (i.e., monthly) scheduling and cross-training effects. They proposed a mathematical framework for defining cross-training policies and introduced a new cross-training policy in which a nurse, dedicated to a nursing unit, received cross-training from one other unit. Additionally, they took a step further by creating a mid-term model with cross-training policies. From two computational studies with 6,400 instances, the results demonstrated that proposed cross-training policies outperformed existing policies in terms of demand coverage and overtime.
Motivated by a real case study in the surgery department in an Italian university hospital, Zanda [4] proposed a long-term (i.e., a year) nurse scheduling approach based on linear integer programming (IP). Besides optimizing the long-term nursing scheduling, special attention had been given to minimize the support of nurses from other departments, ensure nurses' working hours close to assigned hours proportional to the length of the considered time horizon, and avoid assignment of isolated free days. The research results indicated that in most cases the suggested methods discovered new schedules not found through manual computation by the hospital planner, reduced staff redundancy, and satisfied constraints related to contractual rules, specific local requirements, and different nurses' working conditions.
2.2. Scheduling of Medical Staff
The solution procedures for the scheduling problem of medical staff (or manpower scheduling problem) can be divided into two categories, that is, mathematical programming [1,4,12,18,19,30,31] and meta-heuristic algorithms [21,23,32–38]. Research on applying mathematical programming methods focuses on constructing the mathematical model to represent the characteristics of the scheduling problem of medical staff; research on applying meta-heuristic algorithms focuses on searching for an approximate optimal solution within a reasonable time. The scheduling problem of medical staff is an NP-hard problem; therefore, when the number of medical staff is high and multiple hospitals are involved, finding the optimal scheduling solution requires a substantial amount of time. Since this research developed three heuristic algorithms embedded with the PSO algorithm, which is a meta-heuristic algorithm, the following literature references were provided because they address the applications of different meta-heuristic algorithms to the scheduling problem of medical staff.
Gutjahr and Rauner [21] used the ant colony optimization (ACO) algorithm to solve a scheduling problem of medical staff, and they emphasized that the algorithm proposed in the study (called the non-cyclic approach) could more efficiently handle the various possibilities in the scheduling problem of medical staff compared with the TS algorithm, the simulated annealing (SA), and the genetic algorithm (GA). The study incorporated the various soft and hard constraints of the target hospital, including the hospital's regulations and nurses' preferences. In addition, the limitations were divided into static and dynamic modes, and 50 simulations of multi-hospital data were performed using various mode combinations to ascertain the most favorable scheduling method. The results indicated that the proposed ACO algorithm was suitable for solving the scheduling problem of medical staff.
Tsai and Li [33] combined two-stage modeling with the GA to solve a scheduling problem of medical staff, and they considered government regulations, the hospital's regulations, and nurses' preferences in the study. In the first stage, the GA proved to be suitable for solving nurses' scheduling without violating any regulations established by the government or the hospital. In the second stage, solutions to the scheduling problem of medical staff were obtained using the GA after which the solutions were combined with nurses' preferences for problem-solving. The results indicated that the schedules that were generated with consideration for government regulations, the hospital's regulations, and nurses' preferences were more suitable for current scheduling conditions of hospital staff.
Altamirano [23] used the PSO algorithm to solve a problem of scheduling anesthesiology nurses. They used C++ to develop the proposed algorithm, and they compared its results to those generated by CPLEX software. The findings showed that if the time limit were 10 seconds, the proposed PSO algorithm was better than CPLEX software; however, if the time limit were 100 seconds, the best solutions provided by the two methods were similar. Therefore, their results showed that the PSO algorithm provides a better solution than the traditional IP methods when the time period is short.
Parisa [32] stated that the manpower scheduling problem is an NP-hard problem and that scheduling should satisfy the employer's objectives and the employees' preferences. However, when their objectives and preferences were not satisfied, fuzziness occurred in scheduling personnel. Therefore, the study proposed a mathematical model and two fuzzy solution approaches, and the PSO and TS algorithms were used to compare the solutions for scheduling the personnel in chemical factories.
Todorovic and Petrovic [22] used the bee colony optimization (BCO) algorithm to solve a scheduling problem of medical staff. According to the study, there are numerous limiting factors in formulating a scheduling system, including governmental laws and regulations, the hospital's regulations, and individual's scheduling requirements. The high number of limitations made it almost impossible to satisfy all of the conditions. Therefore, the limitations were divided into hard and soft constraints. Hard constraints must be fulfilled, and soft constraints were assigned corresponding penalties. In the study, four BCO algorithms were designed with different parameters, and it was proven that the BCO algorithms were more effective than variable-depth searching and scatter searching.
Buyukozkan and Sarucan [34] were the first authors to apply the artificial bee colony (ABC) algorithm to solve the problems of scheduling nurses. They used Visual Studio C # software to write the proposed ABC algorithm. Based on the results of numerical testing, the schedules generated by the proposed ABC algorithm were better and were obtained more quickly than those prepared by a scheduler in the hospital.
Solving the nurse schedule problem, Lin [35] proposed a GA with an immigrant scheme where the immigrant scheme helps reduce the amount of infeasible solutions due to real-life scheduling constraints. Additionally, the authors had collected information on hospital beds through sensors to determine the manpower required for each work shift.
Xiang [37] designed a modified ACO with a two-level ant graph model to solve the operating room (OR) surgery scheduling problem which considered the operation start time of individual surgery and assignment of required resources to each surgery over a schedule period. The proposed ACO approach performed well on reduction of end time, resources' working time, individual maximum overtime, and nurses' overtime.
Lin [38] considered the challenging issue of home healthcare (HHC) services where nurse or caregivers were sent to patients' homes to provide healthcare services. Combining two NP-hard nurse rostering problem (NRP) and vehicle routing problem with time windows (VRPTW), the HHC is difficult to solve because those two problems are inter-correlated and each has its respective optimal objective which may be in conflict with each other. To solve the HHC problem, the authors proposed an improved harmony search algorithm (HAS) with genetic and saturation schemes which performed well and responded to changes caused by sudden incidents.
The main difference between the aforementioned literature and this research is that, in most of the previous studies, the scheduling problem of medical staff was solved by assuming a known number of medical staff and by only considering the medical staff in one organization/hospital; the only exceptions were references [11,21]. The concept of pooling resources is popular and crucial in supply chain management, but the concept of pooling medical resources is just emerging in hospital management. Pooling and reallocating medical resources are useful for hospital managers in resolving shortages of medical resources for certain hospitals with little extra cost. Further, this study extended reference [11] from two perspectives, that is, determining the weights of penalties for soft constraints in a single objective function instead of solving two single-objective-function problems and developing heuristic algorithms instead of using the mathematical software for solution procedures.
3. RESEARCH METHODOLOGY
3.1. The Proposed IP Model
The scheduling conditions of each hospital should be considered when scheduling medical staff. However, since this study focused on similar divisions in various collaborating hospitals, the scheduling constraints on each hospital were regarded as identical. Nevertheless, the hospitals' sizes influenced the number of groups involved in the schedules of the various hospitals, which also caused differences in the required numbers of medical staff.
The proposed IP model was designed to address an inter-hospital allocation and scheduling problems of medical staff. The equations of the proposed IP model are described in the following. Xijkl is the decision variable, and Xijkl = 1 represents medical employee i working on shift j on day k at hospital l; otherwise, Xijkl = 0. Equation (1) represents the objective function of the proposed IP model, which was to minimize the dissatisfaction of all medical staff. Dissatisfaction was calculated by the sum of penalties (Pl,s) of violating soft constraint s multiplied by the weight (Wl,s) of the corresponding soft constraint s. The weight (Wl,s) is calculated by the analytic hierarchy process (AHP) method [39,40]. Equation (2) indicates that the sum of the working medical staff allocated to each hospital is less than or equal to the total medical staff, Nijk. Equation (2) is a bundling constraint of the medical staff among all hospitals. Equation (3) indicates that the total working medical staff must satisfy the requirements of medical staff of the hospital, Rijk. Clm(.) function of Equation (4) indicates that the working condition of medical employee i must satisfy government regulation m, Glm(.). The Cln(.) function of Equation (5) indicates that the working condition of medical employee i must satisfy hospital regulation n, Hln(.). Equation (6) indicates that all decision variables should be binary integers.
Subject to
3.2. Three Heuristic Algorithms
Although the proposed IP model can provide optimal solutions, the calculation time increases the amount of time required for solving large scheduling problems of medical staff. In this study, we also investigated the allocation of medical staff. Generally, a suitable meta-heuristic algorithm is used to solve large scheduling problems of medical staff to rapidly obtain a set of feasible solutions or approximate optimal solutions.
Although a meta-heuristic algorithm cannot guarantee optimal solutions, its use can reduce the time required to perform the calculations and increase the efficiency of problem-solving for practical situations. Consequently, this research restated the proposed IP model into a hierarchical two-stage model, that is, the allocation and scheduling models of medical staff. In the first stage, we evaluated and calculated the total numbers of personnel in various hospitals and developed three heuristic algorithms for the allocation of medical staff. Subsequently, the number of medical personnel allocated to each hospital was determined. In the second stage, the improved PSO algorithm was used to solve the scheduling problem of medical staff for each hospital based on the number of medical personnel determined in the first stage. Figure 1 shows the framework of the proposed methodology.
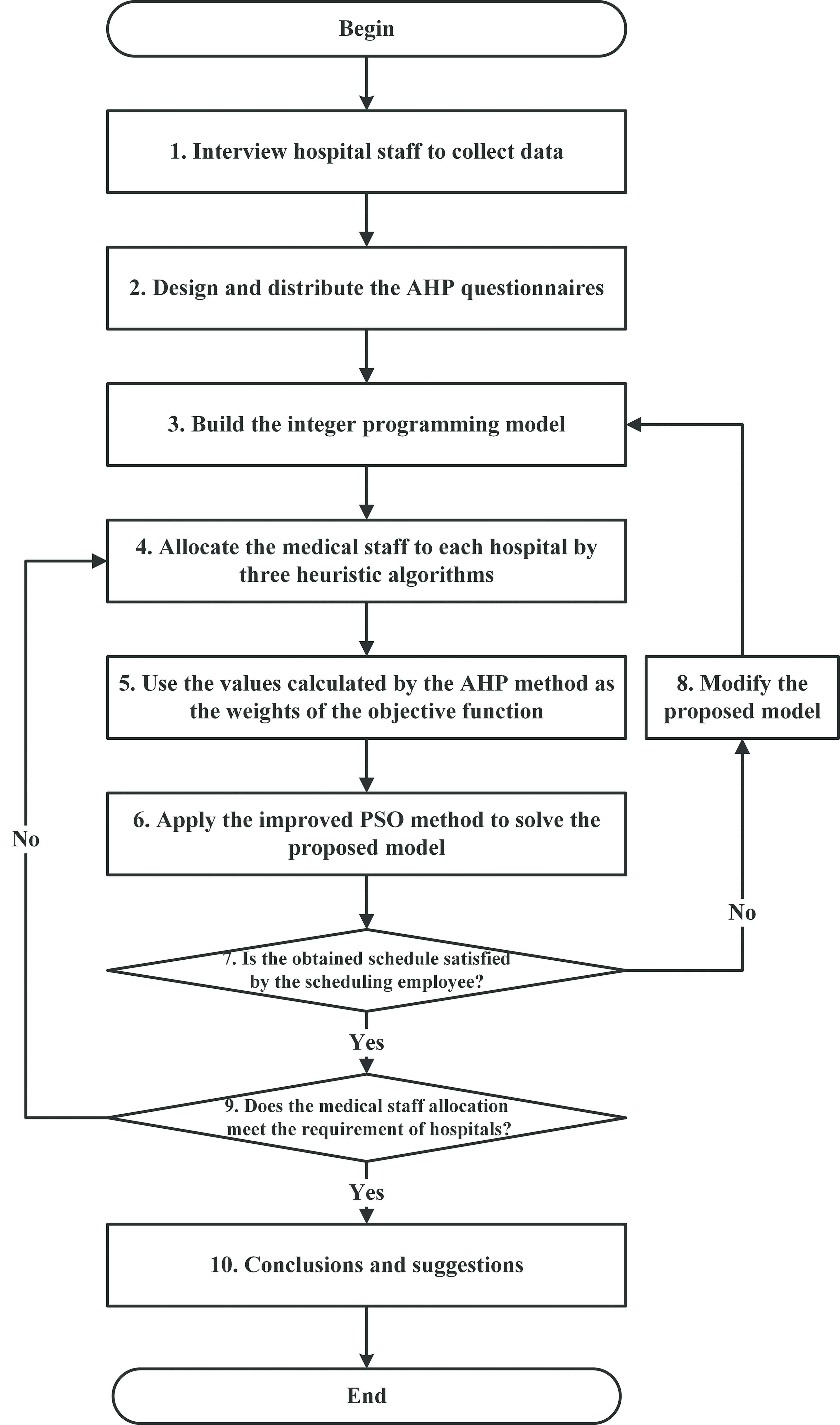
Framework of the proposed methodology.
3.2.1. Calculating the number of medical staff
The analysis of the number of medical staff focuses on investigating whether the current number of medical staff can fulfill the requirements of each hospital and reviewing the current allocation of medical staff. Job analysis calculates the number of monthly medical staff required for implementing each job based on job descriptions and specifications formulated according to the results of job analysis, as shown in Equation (7). When job analysis is performed, the frequency of occurrence and the processing time of each job item should be investigated as the basis for calculating the workload of each job.
Further, workload is reflected by the number of patients, which is calculated by month; the frequency of occurrence should be recorded by month; the processing time can be recorded using the hour for the sake of convenience, but break time during work should be deducted. Break time can be calculated using the work sampling method based on the acquired data.
3.2.2. Allocation methods of medical staff—Stage 1
In this study, medical staff was allocated by assigning a basic number of medical staff to each hospital based on the requirements generated by the hospital's combination of groups and shifts. After ensuring that the resulting schedules do not violate the hard constraints of each hospital (government regulations and the hospital's regulations), we then allocated the remaining medical staff, which involved three algorithms, that is, allocation based on the hospital's size (HRA1), average allocation (HRA2), and allocation based on the severity of penalties (HRA3). The three allocation algorithms of medical staff are explained in detail as follows:
HRA1:
This mechanism allocates the remaining number of medical staff after deducting the basic number of medical staff required by each hospital from the total number of personnel. The remaining staff members are distributed according to the ratio of the numbers of patients' visits among the various hospitals. Thus, large hospitals can obtain more medical staff than small hospitals in order to respond to the numerous visits from patients.
HRA2:
This mechanism allocates the remaining number of medical staff after deducting the basic number of medical staff required by each hospital from the total number of medical staff. The remaining staff members are distributed evenly to each hospital in the interest of fairness. If the remaining number cannot be evenly allocated to the hospitals, the remainder is allocated to the largest hospital.
HRA3:
This mechanism allocates the remaining number of medical staff after deducting the basic number of medical staff required by each hospital from the total number of medical staff. The remaining staff members are distributed according to the severity of penalties calculated using the improved PSO algorithm, which will be described in the next section. The hospital with the heaviest penalty is provided with a medical professional. Subsequently, penalties are recalculated, and the hospital with the heaviest penalty is provided with a medical professional. The entire process repeats until the allocation of the remaining medical staff is complete.
3.2.3. Basic PSO description
After allocating the medical staff allocation, the next step is to schedule individual medical staff accordingly. To this end, the PSO algorithm is used to solve the scheduling problem. Inspired by the swarming characteristic of flocking animals such as birds, PSO is notable for its simplicity. The basic algorithm consists of evaluating an individual particle's fitness, updating the individual's and group's bests, and updating each particle's velocity and position. Two core equations of basic PSO, Equations (8) and (9), are given below. Equation (8) handles the velocity of the individual particle while Equation (9) handles the position of individual particle. Embodied with the exploitation and exploration mechanisms typical of most meta-heuristic algorithms, the velocity update in Equation (8) includes three components: (1) the inertia component
Figure 2 illustrates the basic PSO pseudocode. Each particle in a particle swarm represents a solution. At Line 1 the iteration variable

Pseudocode of basic particle swarm optimization algorithm.
Because of the unique, inherent constraints defined by government regulations associated with medical staff scheduling, repair mechanisms are developed to supplement the basic PSO algorithm. Two specific hard constraints must be satisfied: (1) one day off is scheduled for every seven consecutive working days and (2) no consecutive shifts may be scheduled. If either constraint is violated, the repair mechanism is utilized to ensure the feasibility of individual medical staff's schedule. In addition, the solution representation present in the algorithm, equivalent to a one-month schedule, is specifically customized to accommodate the scheduling of medical staff. The in-depth description of the improved PSO algorithm is presented in the next section.
3.2.4. Improved PSO for scheduling medical staff—Stage 2
In this study, we developed an improved PSO algorithm to solve the scheduling problem of medical staff, combined the hard and soft constraints encountered during scheduling with the PSO algorithm, designed two schedule repair mechanisms, and designed a mechanism for updating schedules. When the numbers of medical staff obtained using the allocation algorithms of medical staff and the improved PSO algorithm developed in this study were combined, a set of feasible schedules was generated in order to obtain approximate optimal solutions. The mechanisms of the improved PSO algorithm are explained as follows.
Set initial particle swarms: Before performing the improved PSO algorithm, an initial group of particle swarms should be established. Each particle represents a solution to a one-month schedule. Subsequently, the particle swarms evolved multi-directionally to form a new superior group of particle swarms.
Generate an initial schedule: A number of schedules equal to the number of particle swarms is generated, indicating that every particle bears the data of a schedule. Afterward, the initial schedule is generated based on the random number of medical staff.
Determine if the schedule is a feasible solution: The schedule is determined based on the hard constraints formed by government regulations and the hospital's regulations. If the schedule violates hard constraints, it undergoes schedule repair in step 4; if not, fitness values are calculated in step 5.
Perform schedule repair mechanisms: In this study, we established repair mechanisms during the processes of the improved PSO algorithm to turn every particle swarm solution into a feasible solution. Subsequently, the best feasible solution is identified by comparing the quality of feasible solutions. The correction processes for two hard constraints are elaborated as follows:
Repair Process 1: Every person must have at least one day off every seven days by government regulation.
- Step 4.1a:
Calculate the total number of consecutive work days assigned to each medical professional in the schedule. If the total number of the consecutive work days of every medical professional is greater than or equal to seven, Step 4.1b is performed; if not, this repair process ends.
- Step 4.1b:
For medical professionals whose schedules violate the constraint, one work day is randomly selected from the violated schedule, and randomly exchanged with a non-working day from another medical professional on the same day to satisfy the constraint. If all individual schedules satisfy the constraint, this repair process is complete and the schedule can undergo Repair Process 2; if not, Step 4.1a should be repeated.
- Step 4.1a:
Repair Process 2: A night shift should not be followed by a day shift on the next day or an evening shift on the next day; an evening shift should not be followed by a day shift on the next day according to government regulation.
- Step 4.2a:
Identify whether any individual schedules contain a night shift followed by a day shift or an evening shift on the next day. If yes, proceed to Step 4.2b. Determine whether any individual schedules contain an evening shift followed by a day shift on the next day. If yes, proceed to Step 4.2b. If the aforementioned constraints are not violated, this repair process ends.
- Step 4.2b:
For medical personnel whose schedules violate the constraints, the shift of the day after the violated shift in the schedule is exchanged with another medical professional's shift that can meet the constraints on that particular day. If all individual schedules satisfy the constraints, the repair process is complete, and fitness values can be calculated in step 5; if not, Step 4.2a should be performed again.
- Step 4.2a:
Calculate fitness values: When solving problems using the improved PSO algorithm, fitness functions should be defined in advance to measure the hospital's performance. The penalty incurred by the soft constraints of the scheduling model of medical staff was defined as the fitness value.
Update the best feasible solutions for individual and group particle swarms: During the iteration of searches and fitness-function calculations, the best feasible solutions of each generation of individual particle swarms and the particle locations are recorded. In addition, the best feasible solutions of each generation of particle swarm groups and the particle locations are recorded to update the speeds and locations of particle swarms.
Determine whether the terminating criteria are satisfied: If the terminating criteria (maximal iterations or solving time limitations) are satisfied, go to step 10. Otherwise, go to step 8.
Update the speeds and locations of particle swarms: In the improved PSO algorithm, the mechanism of updating particle swarm is used to facilitate the movement of individual particle swarms and particle swarm groups toward their best feasible solutions to obtain an approximate optimal solution.
Perform the schedule update mechanism: In this study, we applied the location changes generated by the update mechanism of the improved PSO algorithm to schedule updates. This application can be achieved by assigning a displacement vector that is the same as the number of scheduled days to each particle; thus, the individual displacement amount is updated each day, and the vector of the overall schedule and the displacement amount incurred are equal to the displacement amount of a single particle.
Obtain the approximate optimal solution: The improved PSO algorithm obtain the approximate optimal solution, and the proposed algorithm ends.
4. ANALYSES AND DISCUSSION
4.1. Results of the Proposed Methodology
4.1.1. Estimating the weight of penalties of soft constraints
In this study, we distributed the questionnaires to the director of the image center and five schedules to evaluate the weight of penalties of eight soft constraints. In Table 1, the results showed the weight of penalties of each soft constraint. In order to check the consistency of six experts, the consistency index (C.I.) was calculated and its value was 0.09. According to the eight soft constraints, the random consistency index (R.I.) value was 1.41. Since the consistency ratio (C.R.) value was calculated by the C.I. value divided by the R.I. value, the C.R. value was 0.09/1.41 = 0.063 < 0.1. Therefore, the consistency was met and the weight of penalties of eight soft constraints would be applied to the objective function of the proposed IP model.
| Soft Constraints | Weight by the AHP Method | |
|---|---|---|
| (1) | An employee does not work on consecutive four days | 0.02 |
| (2) | An employee works a day shift followed by an evening shift on the next day | 0.05 |
| (3) | An employee works a day shift followed by a night shift on the next day | 0.05 |
| (4) | An employee works an evening shift followed by a night shift on the next day | 0.04 |
| (5) | An employee works on the “day-off, day and day-off” pattern | 0.17 |
| (6) | An employee works on the “day-off, evening and day-off” pattern | 0.15 |
| (7) | An employee works on the “day-off, night and day-off” pattern | 0.27 |
| (8) | An employee works on the “night, day-off and day” pattern | 0.25 |
Weight of penalties of soft constraints obtained by the AHP method.
4.1.2. Estimating the total number of medical staff
Before solving the inter-hospital scheduling problem of medical staff, the total number of medical staff in the Hospital's branches A, B, and C was calculated using Equation (7) to obtain the number of medical staff required to be at work. In Taiwan, the Ministry of Health and Welfare divided hospitals into four types, that is, medical centers, regional hospitals, district hospitals, and basic-level medical institutions/clinics. In this study, the Hospital's branch A was a medical center, the Hospital's branch B was a regional hospital, and the Hospital's branch C was a district hospital (Table 2). The total number of medical staff was calculated based on the information provided by each branch.
| Branch | A | B | C |
|---|---|---|---|
| Average annual computed tomography (CT) patients | 26,796 | 20,613 | 15,459 |
| Monthly CT patients | 2,233 | 1,718 | 1,288 |
| Average CT patients serviced per group per day | 60 | 48 | 36 |
| Radiologists of each group | 5 | 4 | 3 |
| Group radiologists per day (three shifts a day) | 15 | 12 | 9 |
| Estimated working days per month (excluding weekends) | 22 | 22 | 22 |
| Required radiologists in the CT department of the branch | 25 | 20 | 15 |
Note: Required medical staff at work in Branch
Workload and required medical staff of the Hospital's three branches.
The total number of required radiologists at work in the Hospital's three branches was 60 people (25+20+15) (Table 2), which constituted 75% of the total medical staff of 80 people according to interviews with directors of the image center of the three branches. However, scheduling must involve arranging non-working days for each shift; thus, flexible radiologists constituted 25% of the total number of radiologists. In this study, the flexible medical staff was added to the total radiologists at work, and the sum (80 people) was regarded as the total number of radiologists available for the three branches to schedules.
4.1.3. Allocation schedules of medical staff
The improved PSO algorithm used in this study was written using the C++ programming language. Parameters of the improved PSO algorithm must be determined before it can be used. The total number of medical staff (80 people) was used as the total number of medical staff available for allocation and scheduling in the three branches. In a typical PSO algorithm, the cognitive learning factor (c1) and social learning factor (c2) of particle swarms should be two identical integers. Kennedy and Eberhart [41] suggested that the factors be determined by the characteristics of the problem encountered, and that the range should be between 0 and 4. Generally, the learning factors of particle swarms are set at a value of 2; therefore, in this study, the learning factors, c1 and c2, were set at 2.
Regarding the designation of the inertia weight (w) of particle swarms, Yuhui and Eberhart [42] mentioned that using a high inertia weight can achieve rapid convergence to a local optimum, although the global optimum can be easily missed; in contrast, using a low inertia weight can enhance the ability of local searching, but it may provide local optimal solutions. After testing PSO algorithm based on multiple factors, Yuhui and Eberhart [43] indicated that 0.8 was a satisfactory option for an inertia weight. Therefore, this study set the inertia weight, w, at 0.8.
According to an analysis of the iteration numbers of the improved PSO algorithm, approximately 180 iterations in a total of 1,000 iterations achieved convergence. Therefore, in this study, we set the number of iterations at 400 as the terminating criterion to safely achieve convergence.
Regarding the number of particles set in the improved PSO algorithm, because HRA3 was the most time-consuming algorithm (Table 3) in this study, we assigned 10, 20, and 30 particles to the algorithms for problem-solving, and each setting was tested 30 times. By using the Wilcoxon rank-sum test [44] by Minitab 17 software, we determined that the particle number did not cause significant differences in target values at the α = 0.05 level (i.e., at the 95% confidence interval), although it resulted in substantial differences in problem-solving time, as shown in Table 3. Consequently, a value of 10 particles was used to solve the inter-hospital hierarchical allocation and scheduling problems of medical staff.
| Number of Particles | 10 | 20 | 30 |
|---|---|---|---|
| Solution time (second) | 242.16 | 314.49 | 660.52 |
| Mean values of the objective function | 83.73 | 83.66 | 83.24 |
| SD* of the objective function | 2.71 | 2.78 | 2.28 |
| Comparisons | 95% C.I.* | W-value | P-value |
| H0: μ1 (10 particles) – μ2 (20 particles) = 0 | [−1.54, 1.62] | 904.5 | 0.871 |
| H0: μ1 (10 particles) – μ3 (30 particles) = 0 | [−1.01, 1.69] | 945.0 | 0.657 |
| H0: μ2 (20 particles) – μ3 (30 particles) = 0 | [−1.03, 1.93] | 950.5 | 0.605 |
Note: SD* means standard deviation; C.I.* means the conference interval.
Performance of the HRA3 algorithm among different particles.
The three allocation algorithms of medical staff were the allocation based on the hospital's size (HRA1), average allocation (HRA2), and allocation based on the severity of penalties (HRA3). Because the improved PSO algorithm provides different results in every experiment, we conducted the same experiment on each algorithm 30 times and designated the average of the 30 experimental results as the objective function value, as shown in Table 4.
| Allocation Algorithm | HRA1 | HRA2 | HRA3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Hospital Branches | A | B | C | A | B | C | A | B | C |
| Suggested medical staff (from the 80 people available) | 32 | 26 | 22 | 30 | 26 | 24 | 40 | 23 | 17 |
| Mean values of the objective function | 105.33 | 103.16 | 83.73 | ||||||
| SD of the objective function | 3.49 | 4.38 | 2.71 | ||||||
Performance of three allocation algorithms (Average of results from 30 experiments).
In the analysis of the Wilcoxon rank-sum test (Table 5), when α = 0.05, HRA3 was superior to HRA1 because smaller objective functions values are better solutions; HRA3 was superior to HRA2; but HRA1 and HRA2 did not differ substantially. These results indicated that, in addition to meeting government regulations and the requirements of the Hospital's three branches, the allocations and schedules of medical staff calculated using HRA3 considerably fulfilled the individual requirements of medical staff, and the algorithm resulted in less medical staff dissatisfaction than did HRA1 and HRA2. Therefore, HRA3 is recommended to attain the average greatest benefit for the allocation of medical staff across the three branches.
| Comparisons | 95% C.I. | W-value | P-value |
|---|---|---|---|
| H0: μ1 (HRA1) – μ2 (HRA2) = 0 | [−0.04, 4.31] | 1,043.5 | 0.059 |
| H0: μ1 (HRA1) – μ3 (HRA3) = 0 | [19.73, 23.46] | 1,365.0 | 0.000 |
| H0: μ2 (HRA2) – μ3 (HRA3) = 0 | [17.62, 21.49] | 1,365.0 | 0.000 |
Wilcoxon rank-sum test among three allocation algorithms.
4.2. Scenario Analysis
In this study, we investigated the following two scenarios. In Scenario 1, the total number of medical staff was fixed, and the size of the hospital's branch remained adjustable to obtain the allocations and schedules of medical staff by using the three allocation algorithms of medical staff. In Scenario 2, the total number of medical staff was changed to explore the influences of the various total numbers on the three allocation algorithms proposed in this study.
Scenario 1: Changing the size of the hospital's branch
Sizes of the hospital's branches, that is, two medical centers and one district hospital
This study conducted 30 experiments using the three allocation algorithms based on this combination of the hospital's branch sizes (15/15/9), as shown in Table 6. The value of the objective function was the average of the results of the 30 experiments. We used the Wilcoxon rank-sum test to determine the advantages and disadvantages of the three algorithms. In Table 6, HRA1 and HRA2 did not differ substantially, and HRA3 was superior to both of them at the α = 0.05 level. According to the solution obtained by using HRA3, the suggested personnel numbers for the schedule were 30, 29, and 21 for the Hospital's branches A, B, and C, respectively.
Hospital branch sizes: three district hospitals
In this study, we performed 30 experiments using the three allocation algorithms based on the 12/12/12 combination of hospital branch sizes, as shown in Table 7. According to the results of the Wilcoxon rank-sum test at the α = 0.05 level in Table 7, no significant differences existed between HRA1 and HRA2, HRA1 and HRA3, and HRA2 and HRA3. Therefore, the solutions obtained using the three allocation algorithms could be regarded as identical, which indicated that when the three branches were identical in size, all of the three allocation algorithms generated identical results. Consequently, for circumstances involving three branches of the same size, we suggested that the medical staff remaining after the deduction of the basic medical staff be evenly distributed, which would facilitate the allocation of medical staff in practice.
Hospital branch sizes: a medical center and two district hospitals
In this study, we conducted 30 experiments using the three allocation algorithms based on the 15/9/9 combination of hospital branch sizes, as shown in Table 8. According to the results of the Wilcoxon rank-sum test at the α = 0.05 level in Table 8, HRA1 and HRA2 did not differ considerably, and HRA3 was superior to the other two algorithms. The suitable medical staff of the schedule obtained using HRA3 was 38, 21, and 21 for branches A, B, and C, respectively.
| Branch | A | B | C |
|---|---|---|---|
| Hospital's branch size | 15 | 15 | 9 |
| Allocation algorithm | HRA1 | HRA2 | HRA3 |
| Mean values of the objective function | 103.96 | 102.92 | 82.104 |
| SD of the objective function | 5.97 | 4.02 | 4.62 |
| Comparisons | 95% C.I. | W-value | P-value |
| H0: μ1 (HRA1) – μ2 (HRA2) = 0 | [−0.88, 4.39] | 1,013.0 | 0.147 |
| H0: μ1 (HRA1) – μ3 (HRA3) = 0 | [19.48, 24.91] | 1,356.0 | 0.000 |
| H0: μ2 (HRA2) – μ3 (HRA3) = 0 | [18.10, 22.40] | 1,365.0 | 0.000 |
Results of two medical centers and one district hospital among three allocation algorithms.
| Branch | A | B | C |
|---|---|---|---|
| Hospital's branch size | 12 | 12 | 12 |
| Allocation algorithm | HRA1 | HRA2 | HRA3 |
| Mean values of the objective function | 82.57 | 83.21 | 82.34 |
| SD of the objective function | 3.46 | 2.1 | 2.13 |
| Comparisons | 95% C.I. | W-value | P-value |
| H0: μ1 (HRA1) – μ2 (HRA2) = 0 | [−2.34, 0.95] | 845.0 | 0.301 |
| H0: μ1 (HRA1) – μ3 (HRA3) = 0 | [−1.50, 1.82] | 925.5 | 0.882 |
| H0: μ2 (HRA2) – μ3 (HRA3) = 0 | [−0.24, 2.13] | 1,031.5 | 0.089 |
Results of three district hospitals among three allocation algorithms.
| Branch | A | B | C |
|---|---|---|---|
| Hospital's branch size | 15 | 9 | 9 |
| Allocation algorithm | HRA1 | HRA2 | HRA3 |
| Mean values of the objective function | 100.53 | 102.12 | 81.35 |
| SD of the objective function values | 3.50 | 4.40 | 2.18 |
| Comparisons | 95% C.I. | W-value | P-value |
| H0: μ1 (HRA1) – μ2 (HRA2) = 0 | [−3.85, 0.08] | 784.5 | 0.055 |
| H0: μ1 (HRA1) – μ3 (HRA3) = 0 | [17.20, 20.60] | 1,365.0 | 0.000 |
| H0: μ2 (HRA2) – μ3 (HRA3) = 0 | [19.20, 22.54] | 1,365.0 | 0.000 |
Results of a medical center and two district hospitals among three allocation algorithms
Scenario 2: Changing the total number of medical staff
According to the schedule generated in Subsection 4.1.2, the proportion of violated soft constraints, which was 64.03% in total, including soft constraints (1), (5), (6), (7), and (8) as shown in Table 9, was closely related to non-working days. The percentage of a soft constraint was calculated by the penalties incurred by violating the soft constraint divided by the sum of the penalties incurred by violating each soft constraint. Based on this result, we inferred that an excess existed in the total number of medical staff. Therefore, the differences in the total numbers of medical staff were investigated in Scenario 2.
| Soft Constraints | Percentage (%) | |
|---|---|---|
| (1) | An employee does not work on consecutive four days | 11.99 |
| (2) | An employee works a day shift followed by an evening shift on the next day | 9.7 |
| (3) | An employee works a day shift followed by a night shift on the next day | 8.47 |
| (4) | An employee works an evening shift followed by a night shift on the next day | 14.78 |
| (5) | An employee works on the “day-off, day and day-off” pattern | 15.32 |
| (6) | An employee works on the “day-off, evening and day-off” pattern | 16.29 |
| (7) | An employee works on the “day-off, night and day-off” pattern | 16.69 |
| (8) | An employee works on the “night, day-off and day” pattern | 3.74 |
Percentage of the penalties of violating a soft constraint in the 80-people scenario.
In this scenario, the combination of branch sizes involved one medical center, one regional hospital, and one district hospital (Hospital's branch size: 9, 12, and 15, respectively). The total number of medical staff was altered to explore the differences among the three allocation algorithms caused by such alterations. The results showed that when the total number of medical staff was 50, no solutions were obtained. The other results are presented in Table 10.
| Allocation Algorithm | HRA1 | HRA2 | HRA3 | |||
|---|---|---|---|---|---|---|
| # of Medical Staff | Mean | SD* | Mean | SD | Mean | SD |
| 50 | Infeasible | 0 | Infeasible | 0 | Infeasible | 0 |
| 60 | 60.79 | 2.78 | 60.43 | 1.94 | 60.42 | 2.50 |
| 70 | 92.59 | 3.88 | 90.65 | 4.27 | 73.14 | 2.37 |
| 80 | 105.33 | 3.49 | 103.16 | 4.38 | 83.73 | 2.71 |
at the 5% significance level (α = 0.05 )
Performance of three allocation algorithms while changing the total number of medical staff.
According to Table 10, an excess in the number of medical staff increased the violations of soft constraints in each of the three allocation algorithms, which caused higher values of the objective function and generated no positive correlation with hospital effectiveness or quality of medical care. In contrast, when the number of medical staff is low, branches may not require such a large number of flexible medical staff. Based on this inference, 60 was established as the approximate lowest number of medical staff for the case branches, which also indicated the approximate lowest medical staff cost.
In this study, we used the number of 60 people to conduct and analyze allocation and schedules of medical staff (Table 11), and we found that the proportion of soft constraint violations related to non-working days decreased from 64.03% (80 people) to 48.23% (60 people). Consequently, decreasing the total number of medical staff proved to be effective for reducing the dissatisfaction of medical staff related to scheduling.
| Soft Constraints | Percentage (%) | |
|---|---|---|
| (1) | An employee does not work on consecutive four days | 2.47 |
| (2) | An employee works a day shift followed by an evening shift on the next day | 15.63 |
| (3) | An employee works a day shift followed by a night shift on the next day | 11.29 |
| (4) | An employee works an evening shift followed by a night shift on the next day | 24.85 |
| (5) | An employee works on the “day-off, day and day-off” pattern | 8.85 |
| (6) | An employee works on the “day-off, evening and day-off” pattern | 11.02 |
| (7) | An employee works on the “day-off, night and day-off” pattern | 12.29 |
| (8) | An employee works on the “night, day-off and day” pattern | 13.6 |
Percentage of the penalties of violating a soft constraint in the 60-people scenario.
4.3. Managerial Implications
This study proposed a satisfactory mathematical model and used an improved PSO algorithm to solve inter-hospital hierarchical allocation and scheduling problems of medical staff. In addition, the scenario analyses provided informative results that managers could use in the allocating and scheduling of medical staff. According to the scenario analyses, HRA3 was superior overall when the sizes of the three hospital branches were dissimilar. When the three hospital branches were the same size, no significant differences existed among the three allocation algorithms; furthermore, the results regarding differences among the three allocation algorithms caused by varying the total number of medical staff could serve as a reference for managers when allocating medical staff.
Whereas previous studies have focused on medical staff planning for a single company, in this study, we used inter-hospital allocation planning of pooled medical staff to facilitate the cooperative operation and mutual support of medical staff among a hospital's branches. The limitation of this research was that the test datasets were generated by the case study and scenario settings, respectively. This study compared three proposed algorithms using these datasets but did not compare the proposed algorithms with those presented in the literature. To the best of our knowledge, no dataset related to the inter-hospital medical staff allocation and scheduling problem is presented in the OR library [45]. Hence, the proposed problem merits further exploration of different heuristic or meta-heuristic algorithms.
5. CONCLUSIONS AND FUTURE RESEARCH
5.1. Conclusions
The four contributions of this research can be summarized as follows:
Most studies on allocation problems of medical staff have focused on a single aspect, and few have investigated the allocation planning of medical staff, solved scheduling problems of medical staff, or considered the weights of individual scheduling preferences. We considered these problems when developing three heuristic algorithms embedded with the improved PSO algorithm. The research results indicated that our approach solved the inter-hospital allocation and scheduling problems of medical staff, and reduced allocation waste of medical staff.
In this study, we constructed a simulation of pooling medical staff among collaborating hospital branches, and designed the methodology procedures for solving the problems of inter-hospital hierarchical allocation and scheduling of medical staff. The research results could provide hospitals with suitable numbers of medical staff and satisfactory schedules to reduce the dissatisfaction that medical staff members have toward schedules and to prevent unnecessary disputes.
The improved PSO algorithm designed in this study can generate schedules that satisfy the various hard constraints created by government regulations and hospitals' regulations and prevent the negligence and mistakes that often occur in manual scheduling. In addition, using the improved PSO algorithm for scheduling can reach a higher level of accuracy than will be possible with traditional manual scheduling and substantially reduce scheduling time.
In this study, the medical staff of the hospital's branches were interviewed and questionnaires designed using the AHP method were distributed to determine the scheduling preferences of medical staff and to formulate relevant soft constraints. Subsequently, we used the AHP method to calculate and analyze the weights of the factors rather than using an equal weight for each factor or using intuitive ratings. The soft constraints were considered to generate flexible schedules that could more thoroughly satisfy the requirements of the medical staff.
5.2. Future Research
Based on the results and limitations of this research, two directions are suggested for further research:
The soft constraints for scheduling should be more diversified. For example, penalties that are incurred by dispatching medical personnel from one hospital to another can be added. In addition, specialized skills, familiarity, years of work experience, mutual coordination, and job performance of the medical staff should be considered [19]. Hospitals expect to deploy both medical staff with numerous years of work experience and those with few years of work experience in one department to prevent lack of skills and stabilize the quality of medical care in each hospital. Therefore, it is suggested that future studies add suitable soft constraints for enhancing the effectiveness of hospital collaboration and for further stabilizing the quality of medical care.
Future studies should consider other meta-heuristic algorithms, such as harmony search, variable neighborhood search [46], or hybrid meta-heuristic algorithms, for solving problems related to inter-hospital hierarchical allocation and scheduling of medical staff, and they should compare the problem-solving quality and time requirements of various algorithms. In addition, to address this research question, subsequent studies can establish user interfaces, thereby enabling increasingly convenient use for managers and expanding the application of the method proposed in this study.
CONFLICT OF INTEREST
The authors declare no conflicts of interest.
AUTHORS' CONTRIBUTIONS
Ping-Shun Chen: Conceptualization, Methodology, Formal Analysis, Writing- Reviewing and Editing, Supervision, Project Administration, Wen-Tso Huang: Conceptualization, Reviewing and Editing, Literature Research, Tsung-Huan Chiang: Coding/Implementation, Writing, Data Analysis, Gary Yu-Hsin Chen: Conceptualization, Methodology, Reviewing and Editing, External Correspondence, Project Coordination, Funding Acquisition.
Funding Statement
This research is supported by the Ministry of Science and Technology, Taiwan, under contract numbers: MOST 106-2221-E-327-030- and MOST 108-2221-E-992-019-.
REFERENCES
Cite this article
TY - JOUR AU - Ping-Shun Chen AU - Wen-Tso Huang AU - Tsung-Huan Chiang AU - Gary Yu-Hsin Chen PY - 2020 DA - 2020/03/17 TI - Applying Heuristic Algorithms to Solve Inter-hospital Hierarchical Allocation and Scheduling Problems of Medical Staff JO - International Journal of Computational Intelligence Systems SP - 318 EP - 331 VL - 13 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.200310.004 DO - 10.2991/ijcis.d.200310.004 ID - Chen2020 ER -
