Journal of Statistical Theory and Applications

Download article (PDF)
Next Article In Issue>
Volume 18, Issue 4, December 2019, Pages 329 - 342

The Generalized Kumaraswamy-G Family of Distributions

Authors
Zohdy M. Nofal1, Emrah Altun2, Ahmed Z. Afify1, *, M. Ahsanullah3
1Department of Statistics, Mathematics and Insurance, Benha University, Benha, Egypt
2Department of Statistics, Bartin University, Bartin, Turkey
3Department of Management Sciences, Rider University, Lawrenceville, NJ, USA
*Corresponding author. Email: ahmed.afify@fcom.bu.edu.eg
Corresponding Author
Ahmed Z. Afify
Received 6 June 2018, Accepted 19 January 2019, Available Online 20 November 2019.
DOI
10.2991/jsta.d.191030.001How to use a DOI?
Keywords
Kumaraswamy-G Family; Maximum Likelihood; Order Statistics; Regression
Abstract

We propose a new class of continuous distributions called the generalized Kumaraswamy-G family which extends the Kumaraswamy-G family defined by Cordeiro and de Castro [1]. Some special models of the new family are provided. Some of its mathematical properties including explicit expressions for the ordinary and incomplete moments, generating function, Rényi entropy, order statistics and characterizations are derived. The new location-scale regression model is introduced based on the new generated distribution. The maximum likelihood is used for estimating the model parameters. The flexibility of the generated family is illustrated by means of two applications to real data sets.

Copyright
© 2019 The Authors. Published by Atlantis Press SARL.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

1. INTRODUCTION

Recently, the interest in developing more flexible generators remains strong. Many generalized distributions have been developed over the past decades for modeling data in several areas such as biological studies, environmental sciences, economics, engineering, finance and medical sciences. There has been an increased interest in defining new generated families of univariate distributions by introducing additional shape parameters to the baseline model. For example, the Marshall-Olkin-G [2], beta-G [3], Kumaraswamy-G (K-G) [1], transmuted geometric-G [4], beta transmuted-H [5] and the generalized transmuted-G [6] families. However, in many applied areas, there is a clear need for extending forms of the classical models.

The generated distributions have attracted several statisticians to develop new models because the computational and analytical facilities available in most symbolic computation software platforms. Several mathematical properties of the extended distributions may be easily explored using mixture forms of exponentiated-G (exp-G) distributions.

Consider a baseline cumulative distribution function (cdf) Gx;φ and probability density function (pdf) gx;φ depending on a parameter vector φ, where φ =φk=φ1,φ2,…. Thus, Cordeiro and de Castro [1] defined the K-G family by the cdf and pdf given by

Fx;a,b,φ=1−1−Gx;φab
and
f(x;a,b,φ)=abgx;φGx;φa−11−Gx;φab−1,
respectively, where g(x)=dG(x)∕dx and a and b are two additional positive shape parameters. Clearly, for a=b=1, we obtain the baseline distribution. The additional parameters a and b aim to govern skewness and tail weight of the generated distribution. An attractive feature of this family is that a and b can afford greater control over the weights in both tails and in the center of the distribution. Further details can be found in Cordeiro and de Castro [1].

In this paper, we define and study a new family of distributions by adding one extra shape parameter in (1) to provide more flexibility to the generated family. To this end, we construct a new generator so-called the generalized Kumaraswamy-G (GK-G) family and give a comprehensive description of some of its mathematical properties. We hope that the new model will attract wider applications in reliability, engineering and other areas of research.

The cdf of the GK-G family is defined (for x>0) by

Fx;a,b,α,φ=1−1−αGx;φab1−1−αb.

The corresponding pdf of (3) is given by

fx;a,b,α,φ=αabgx;φ1−1−αbGx;φa−11−αGx;φab−1,
where 0<α≤1, a>0 and b>0 are shape parameters.

Henceforth, a random variable X having the density function (4) is denoted by X∼ GK-G(a,b,α,φ).

The hazard rate function (hrf) of X, say τ(x), is given by

τ(x)=αabgx;φGx;φa−11−αGx;φab−11−αGx;φab−1−αb.

Some special cases of the new family are listed in Table 1.

a b α Reduced Model Authors
a b 1 K-G family Cordeiro and de Castro [1]
1 b α Ex-G family New
a 1 − exp-G family Gupta et al. [7]
1 1 − Gx;φ –
Table 1

Sub-models of the GK-G family.

The rest of the paper is outlined as follows. In Section 2, three special models of GK-G family including Weibull, log-logistic and gamma are presented. In Section 3, some of mathematical properties of the proposed family including linear representation, ordinary and incomplete moments, mean deviations, moment generating function (mgf), Rényi entropy and order statistics are obtained. Maximum likelihood estimation of the model parameters is investigated in Section 4. In Section 5, we provide a simulation study to evaluate the performance of the maximum likelihood method in estimating the parameters of the GK-G family. The log-generalized Kumaraswamy-Weibull regression model is defined in Section 6. Section 7 is devoted to applications to prove empirically the flexibility of the proposed models. Finally, some concluding remarks are given in Section 8.

2. SPECIAL MODELS

In this section, we provide four special models of the GK-G family, namely, GK-Weibull, GK-log logistic and GK-gamma distributions. These sub-models generalize important existing distributions in the literature.

2.1. The GK-Weibull (GKW) Distribution

The Weibull (W) distribution, with positive parameters λ and β, has pdf and cdf given (for x>0) by gx=λβxβ−1e−λxβ and Gx=1−e−λxβ, respectively. Then, the GKW pdf reduces to

f(x)=αabλβxβ−1e−λxβ1−1−αb1−e−λxβa−11−α1−e−λxβab−1.

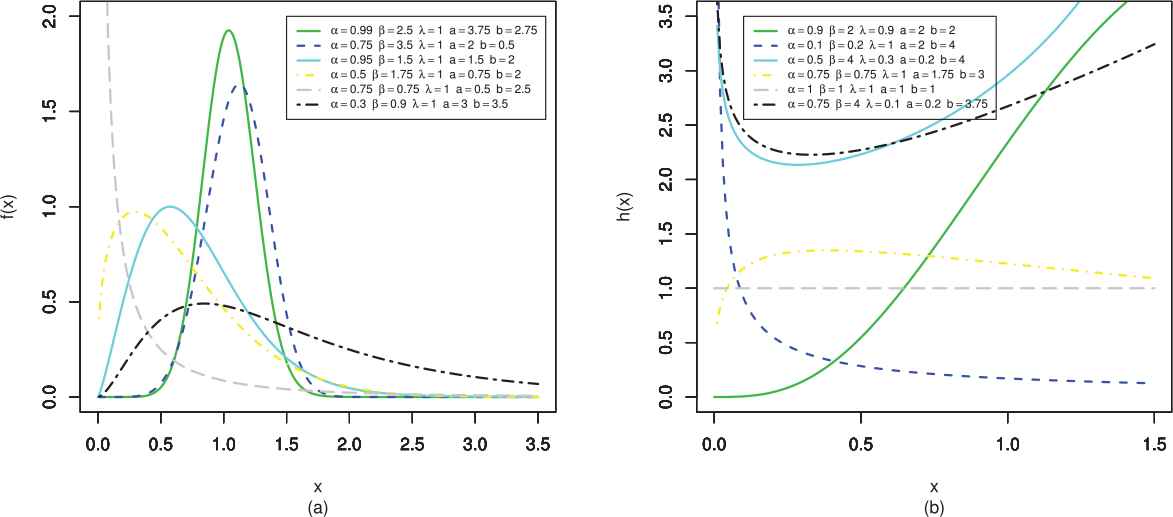
The GKW distribution reduces to the GK-exponential (GKE) distribution when β=1. Also, when a=b=0, it reduces to the W distribution. Figure 1 displays some possible shapes of the density and hazard rate functions of this distribution.

Figure 1

pdf (left) and hrf (right) plots of GK-Weibull (GKW) distribution.

2.2. The GK-Log Logistic (GKLL) Distribution

The log-logistic (LL) distribution with positive parameters λ and β has pdf and cdf given by g(x)=βλ−βxβ−1[1+(xλ)β]−2 (for x>0) and G(x)=1−1+(xλ)β−1, respectively. Then, the pdf of the GKLL distribution is given by

f(x)=αabβλ−βxβ−11−(1−α)b1+xλβ−2{1−[1+xλβ]−1}a−1   × (1−α{1−[1+xλβ]−1}a)b−1. 

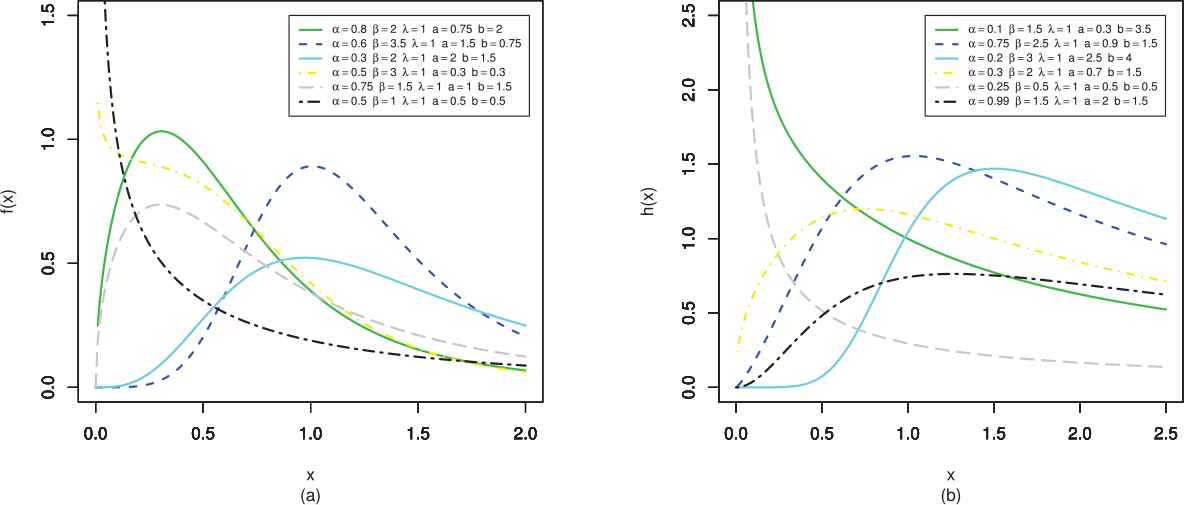
The GKLL model reduces to the LL distribution when a=b=1. Plots of the density and hazard rate functions of the GKLL distribution are displayed in Figure 2 for some parameter values.

Figure 2

pdf (left) and hrf (right) plots of GK-log logistic (GKLL) distribution.

2.3. The GK-Gamma (GKGa) Distribution

By taking G(x) and g (x) in (4) to be the cdf G (x)=γλ,x∕β∕Γλ and the pdf g(x)=xλ−1e−x∕β∕βλΓλ of the gamma (Ga) distribution, where λ>0 is a shape parameter and β>0 is a scale parameter. Then, the pdf of the GKGa (for x>0) reduces to

f(x)=αabγλ,x∕β∕Γλa−1βλΓλ1−1−αbxλ−1e−x∕β1−αγλ,x∕β∕Γλab−1.

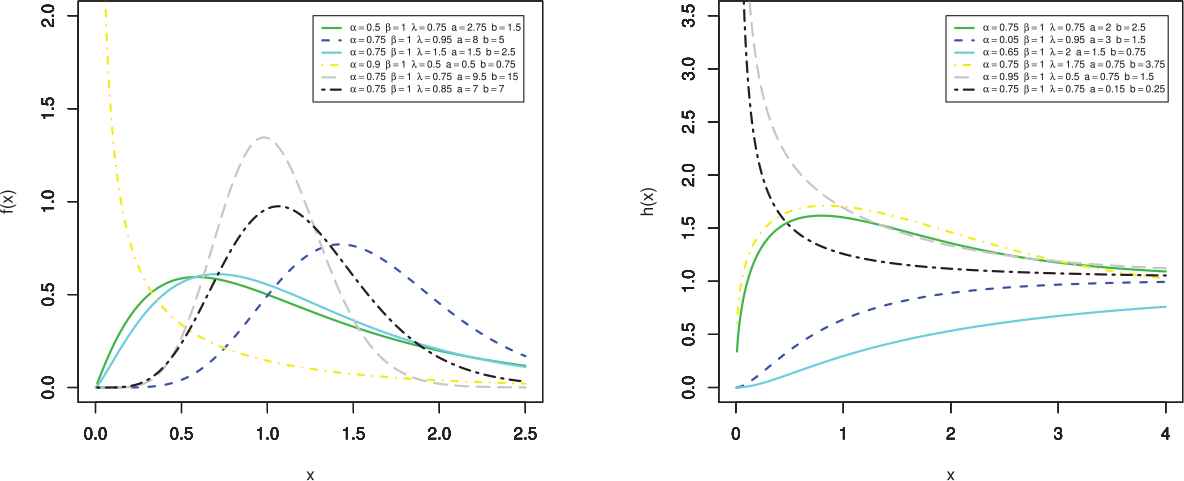
This distribution reduces to the Ga distribution if a=b=1. For λ=1, we obtain the GK-exponenial (GKE) distribution. Figure 3 displays plots of the density and hazard rate functions for the GKGa distribution for selected parameter values.

Figure 3

pdf (left) and hrf (right) plots of GK-gamma (GKGa) distribution.

3. MATHEMATICAL PROPERTIES

3.1. Linear Representation

In this section, we provide a useful representation for the GK-G pdf. Consider the power series, for z<1 and ρ>0 real non-integer,

1−zρ−1=∑k=0∞−1kρ−1kzk.

After applying the power series (5) to (4), we obtain

f(x)=b1−1−αb∑k=0∞−1kαk+1b−1kagxGxak+1−1.

Further, we can write the last equation as

f(x)=∑k=0∞υkhak+1x,
where
υk=−1kαk+11−1−αbbk+1
and hak+1x=ak+1gxGxak+1−1 is the exp-G density with power parameter ak+1>0.

Thus, several mathematical properties of the GK-G family can be derived from those properties of the exp-G family. For example, the ordinary and incomplete moments and mgf of X can be obtained directly from those of the exp-G class.

The cdf of the GK-G family can also be expressed as a mixture of exp-G densities. By integrating (6), we obtain the same linear representation

F(x)=∑k=0∞υkHak+1x,
where Hk+1ax is the cdf of the exp-G family with power parameter k+1a.

The formulae derived throughout the paper can be easily handled in most symbolic computation software platforms such as Maple, Mathematica and Matlab because of their ability to deal with analytic expressions of formidable size and complexity. Established explicit expressions to evaluate statistical measures can be more efficient than computing them directly by numerical integration. We have noted that the infinity limit in these sums can be substituted by a large positive integer such as 50 for most practical purposes.

3.2. Quantile Function

The quantile function (qf) of X, say Q(u)=F−1u, can be obtained by inverting (3) numerically and it is given by

Q(u)=G−1α−11−1−ud1b1a,
where d=1−1−αb.

3.3. Moments

Hereafter, Yk+1a denotes the exp-G distribution with power parameter ak+1. The rth moment of X, say μr′, follows from (6) as

μr′=EX r=∑k=0∞υkEYak+1 r.

3.4. Generating Function

Here, we provide two formulae for the mgf MXt=EetX of X. Clearly, the first one can be derived from (6) as

MXt=∑k=0∞υkMak+1t,
where Mak+1t is the mgf of Yak+1. Hence, MXt can be determined from the exp-G generating function.

A second formula for MXt follows from (6) as

MXt=∑k=0∞υkτt,k,
where τt,k=∫01exptQGuuak+1−1du and QG(u) is the qf corresponding to Gx;ϕ, i.e., QG(u)=G−1(u;ϕ).

3.5. Incomplete Moments

The sth incomplete moment, say φst, of X can be expressed from (6) as

φst=∫−∞tx sfxdx=∑k=0∞υk∫−∞tx shak+1xdx.

The mean deviations about the mean [δ1=E(|X−μ1′|)] and about the median δ2=EX−M of X are given by δ1=2μ1′F(μ1′)−2φ1(μ1′) and δ2=μ1′−2φ1M, respectively, where μ1′=EX, M=Median(X)=Q(0.5) is the median, F(μ1′) is easily evaluated from (3) and φ1t is the first incomplete moment given by (7) with s=1.

Now, we provide two ways to determine δ1 and δ2. First, a general equation for φ1t can be derived from (7) as

φ1t=∑k=0∞υkJak+1t,
where Jak+1t=∫−∞txhak+1xdx is the first incomplete moment of the exp-G distribution.

A second general formula for φ1t is given by

φ1t=∑k=0∞υkνkt,
where νkt=ak+1∫0GtQGuuak+1−1du can be computed numerically.

These equations for φ1t can be applied to construct Bonferroni and Lorenz curves defined for a given probability π by B(π)=φ1q∕(πμ1′) and L(π)=φ1q∕μ1′, respectively, where μ1′=E(X) and q=Q(π) is the qf of X at π. These curves are very useful in economics, reliability, demography, insurance and medicine.

3.6. Entropies

The Rényi entropy of a random variable X represents a measure of variation of the uncertainty. The Rényi entropy is defined by

IθX=11−θlog∫−∞∞fxθdx, θ>0 and θ≠1.

Using the pdf (4), we can write

fxθ=αabdθgxθGxθa−11−αGxaθb−1.

Applying the power series (5) to the last term, we obtain

1−αGxaθb−1=∑k=0∞−1kθb−1kαkGxak
fxθ=abdθ∑k=0∞−1kαk+θθb−1kgxθGxak+θ−θ  =∑k=0∞ηk gxθGxak+θ−θ, 
where
ηk=−1kαk+θabdθθb−1k.

Then, the Rényi entropy of the GK-G family is given by

IθX=11−θlog∑k=0∞ηk∫−∞∞gxθGxak+θ−θdx.

3.7. Order Statistics

Order statistics make their appearance in many areas of statistical theory and practice. Let X1,…,Xn be a random sample from the GK-G family. The pdf of Xi:n can be written as

fi:nx=fxBi,n−i+1∑j=0n−i−1 jn−ijF (x) j+i−1,
where B(⋅,⋅) is the beta function. Based on (3), we have
F j+i−1(x)=∑l=0j+i−1−1ls j+i−1j+i−1l1−αGx;φalb,
where s=1−1−αb.

Using (4) and the above equation, we can write

fxF (x) j+i−1=αab∑l=0j+i−1−1ls j+ij+i−1lgx;φGx;φa−1   × 1−αGx;φabl+1−1. 

After a power series expansion, the last equation reduces to

fxF (x) j+i−1=ab∑l=0j+i−1∑k=0∞−1l+kαk+1s j+ij+i−1l   ×bl+1−1kgx;φGx;φak+1−1. 

Then, we have

fxF j+i−1(x)=∑k=0∞dkhak+1x,
where
dk=∑l=0j+i−1−1l+kbαk+1ak+1s j+ij+i−1lbl+1−1k.

Substituting (10) in (8), the pdf of Xi:n can be expressed as

fi:nx=∑k=0∞ ∑j=0n−i−1 jn−ijBi,n−i+1dkhak+1x,
where hak+1x is the exp-G density with power parameter ak+1.

(10) reveals that the density function of the GK-G order statistics is a linear combinations of exp-G densities. So, based on (10), we can derive the properties of Xi:n from those properties of Yak+1.

For example, the qth moments of Xi:n is given by

EXi:nq=∑k=0∞ ∑j=0n−i−1jn−ijBi,n−i+1dkEYk+1a.

4. CHARACTERIZATIONS

Here, we provide two characterization theorems. We will use the following two Lemmas to prove our main results.

Assumptin A.

Suppose the random variable X has an absolutely continuous cdf F(x) and pdf f(x). Let γ=sup{X|F(x)>0} and δ=inf{X|F(x)>1}.

Lemma 1.

Suppose X be a random variable having the assumption A. Let

E(X|X≤x)=m(x)τ(x),
where m(x) is a continuous differentiable function with the condition
∫γxu−m′(u)m(u)du<∞ for all x,

γ<x<δ and τ(x)=f(x)∕F(x). Then

f(x)=ce∫γxu−m′(u)m(u)du,
where c is determined such that 1c=∫γδf(x)dx.

Lemma 2.

Suppose X be a random variable having the assumption A. Let

E(X|X≥x)=n(x)r(x),
where n(x) is a continuous differentiable function with the condition
∫γxu−n′(u)n(u)du<∞ for all x,

γ<x<δ and r(x)=f(x)∕1−F(x). Then

f(x)=ce−∫γxu+n′(u)n(u)du,
where c is determined such that 1c=∫γδf(x)dx.

Theorem 1.

Suppose that X is an absolutely continuous random variable with cdf F(x) and pdf f(x). We assume γ=0, δ=∞ and E(X)<∞. Then

E(X|X≤x)=m(x)τ(x),
where
m(x)=1g(x)G (x)α−11−αG (x)ab−1μ1(x),
μ1(x)=∫0xug(u)G (u)α−11−αG (x)ab−1du
and τ(x)=f(x)∕F(x).

Proof.

It is easy to show that if

f(x)=αabg(u)G (x)α−11−αG (x)ab−11−(1−α)b,
then
m(x)=1g(x)G (x)α−11−αG (x)ab−1μ1(x).

We prove here the only if condition.

Suppose that

m(x)=1g(x)G (x)α−11−αG (x)ab−1μ1(x),
μ1(x)=∫0xug(u)G (u)α−11−αG (u)ab−1du.
mm′(x)=x−m(x)g(x)G (x)α−11−αG (x)ab−1   × g′(x)G (x)+(α−1)g (x)2G (x)α−21−αG (x)ab−1   − (b−1)1−αG (x)ab−2αaG (x)α+a−2g (x)21−αG (x)ab−1. 

We have

x−m′(x)m(x)=1g(x)G (x)α−11−αG (x)ab−1   × g′(x)G (x)+(α−1)g (x)2G (x)α−21−αG (x)ab−1   − (b−1)1−αG (x)ab−2αaG (x)α+a−2g (x)21−αG (x)ab−1 

Thus by Lemma 1

f′(x)f(x)=1g(x)G (x)α−11−αG (x)ab−1   × g′(x)G (x)+(α−1)g (x)2G (x)α−21−αG (x)ab−1   − (b−1)1−αG (x)ab−2αaG (x)α+a−2g (x)21−αG (x)ab−1. 

On integrating both sides of the above equation, we obtain

f(x)=cg(x)G (x)α−11−αG (x)ab−1.

Using the boundary condition ∫0∞f(x)dx=1, we obtain c= αab1−(1−α)b.

Theorem 2.

Suppose that X is an absolutely continuous random variable with cdf F(x) and pdf f(x). We assume γ=0, δ=∞ and E(X)<∞. Then

E(X|X≥x)=n(x)r(x),
where
n(x)=1g(x)G (x)α−11−αG (u)ab−1μ1∗(x),
μ1∗(x)=∫x∞ug(u)G (u)α−11−αG (u)ab−1du
and r(x)=f(x)∕1−F(x).

Proof.

The if condition is easy to show. We will prove here the only if condition.

If

n(x)=1g(x)G (x)α−11−αG (u)ab−1μ1∗(x),
μ1∗(x)=∫x∞ug(u)G (u)α−11−αG (u)ab−1du.

Then

n′(x)=− x−n(x)g(x)G (x)α−11−αG (x)ab−1   × g′(x)G (x)+(α−1)g (x)2G (x)α−21−αG (x)ab−1   − (b−1)1−αG (x)ab−2αaG (x)α+a−2g (x)21−αG (x)ab−1. 

Thus

−x+n′(x)n(x)=1g(x)G (x)α−11−αG (x)ab−1   × g′(x)G (x)+(α−1)g (x)2G (x)α−21−αG (x)ab−1   − (b−1)1−αG (x)ab−2αaG (x)α+a−2g (x)21−αG (x)ab−1. 

By Lemma 2, we have

f′(x)f(x)=1g(x)G (x)α−11−αG (x)ab−1   × g′(x)G (x)+(α−1)g (x)2G (x)α−21−αG (x)ab−1   − (b−1)1−αG (x)ab−2αaG (x)α+a−2g (x)21−αG (x)ab−1. 

On integrating both sides of the above equation, we obtain

f(x)=cg(x)G (x)α−11−αG (x)ab−1.

Using the boundary ondition ∫0∞f(x)dx=1, we obtain c=αab1−(1−α)b.

Remark 1.

m(x) and n(x) can be given for the GKW, GKLL and GKGa distributions.

5. MAXIMUM LIKELIHOOD ESTIMATION

In this section, we determine the MLEs of the parameters of the new GK-G family from complete samples only. Let x1,…,xn be a random sample from the GK-G family with parameters λ,a,b and φ. Let θ=(a,b,α,φ⊺)⊺ be the p×1 parameter vector. Then, the log-likelihood function for θ, say ℓ=ℓθ, is given by

ℓ=nlogα+nloga+nlogb−nlogs+(a−1)∑i=1nlogGxi;φ   +∑i=1nloggxi;φ+(b−1)∑i=1nlog1−αGxi;φa,
where s=1−1−αb.

(12) can be maximized either directly by using the R (optim function), SAS (PROC NLMIXED) or Ox program (sub-routine MaxBFGS) or by solving the nonlinear likelihood equations obtained by differentiating (12).

The score vector components, say Uθ=∂ℓ∂θ=(∂ ℓ ∂a,∂ ℓ ∂b,∂ ℓ ∂α,∂ ℓ ∂φk)⊺=Ua,Ub,Uα,Uφk⊺, are available with the authors upon request.

Setting the nonlinear system of equations Ua=Ub=Uα=Uφk=0 and solving them simultaneously yields the MLE θ̂=(â,b̂,α̂,φ̂⊺)⊺ of θ=(a,b,α,φ⊺)⊺. These equations cannot be solved analytically and statistical software can be used to solve them numerically using iterative methods such as the Newton-Raphson type algorithms. For interval estimation of the model parameters, we require the observed information matrix whose elements are available with the corresponding author.

6. SIMULATION STUDY

In this subsection, a simulation study is conducted to examine the performance of the MLEs of the generalized Kumaraswamy normal (GKN) parameters. We generate 10,000 samples of size, n = 50, 500 and 1,000 of the GKN model. The precision of the MLEs is discussed by means of the following measures: mean, mean square error (MSE), estimated average length (AL) and coverage probability (CP). The empirical study was conducted with software R. The empirical results are given in Table 2. The values in Table 1 indicate that the estimates are quite stable and, more importantly, are close to the true values for the these sample sizes. The simulation study shows that the maximum likelihood method is appropriate for estimating the GKN parameters. In fact, the means of the parameters tend to be closer to the true parameter values when n increases. This fact supports that the asymptotic normal distribution provides an adequate approximation to the finite sample distribution of the MLEs.

α a b μ σ n Mean
 MSE
α a b μ σ α a b μ σ
0.5 0.5 2 0 1 50 0.3641 0.6933 2.2054 −0.1111 1.0367 0.1296 0.3960 0.2200 0.3944 0.0857
500 0.3991 0.5997 2.0905 −0.0906 1.0334 0.0814 0.1150 0.0610 0.1732 0.0408
1000 0.4669 0.5507 2.0448 −0.0245 1.0224 0.0510 0.0547 0.0286 0.0811 0.0205
0.3 2 0.5 0 1 50 0.0517 2.2070 0.1416 −0.0938 0.9765 1.0513 0.8443 0.4594 0.0919 0.0258
500 0.2085 2.1592 0.3098 −0.0988 0.9879 0.4034 0.3933 0.1505 0.0471 0.0118
1000 0.1871 2.1492 0.3888 −0.0642 0.9919 0.3583 0.3828 0.0755 0.0612 0.0089
0.7 1.5 2.5 0 1 50 0.4229 2.0211 2.8649 −0.2270 1.1292 0.2230 0.8115 0.3188 0.3174 0.1674
500 0.5629 1.8111 2.6869 −0.1810 1.0252 0.0730 0.4305 0.1898 0.1404 0.0165
1000 0.6727 1.5157 2.4998 −0.0182 0.9933 0.0294 0.0253 0.0144 0.0108 0.0084
Table 2

Simulation results of the GK-N distribution for several values of parameters.

7. THE LOG-GENERALIZED KUMARASWAMY-WEIBULL (LGKW) REGRESSION MODEL

The GKW distribution with five parameters, 0<α≤1, a>0, b>0, λ>0 and β>0, introduced in Section 3.1. Let X is a random variable following the GKW density function and Y is defined by Y=log(X). The density function of Y obtained by replacing λ=1∕σ and β=exp(μ) reduces to

fy=αabσexpy−μσ−expy−μσ1−1−αb× 1−exp−expy−μσa−11−α1−exp−expy−μσab−1
where y∈ℜ, μ∈ℜ, σ>0, 0<α≤1, a>0 and b>0. We refer to (13) as the LGKW distribution, say Y∼LGKW(α,a,b,σ,μ), where μ∈ℜ is the location parameter, σ>0 is the scale parameter and α, a and b are shape parameters.

The corresponding survival function is

sy=1−α1−exp−expy−μσab−1−αb1−1−αb
and the hrf is simply h(y)=f(y)∕S(y). The standardized random variable Z=(Y−μ)∕σ has density function
fz=αabexpz−expz1−1−αb1−exp−expza−11−α1−exp−expzab−1

Parametric regression models to estimate univariate survival functions for censored data are widely used. A parametric model that provides a good fit to lifetime data tends to yield more precise estimates of the quantities of interest. Based on the LGKW density, we propose a linear location-scale regression model linking the response variable yi and the explanatory variable vector νiT=νi1,…,νip given by

yi=νiTβ+σzi,i=1,… ,n
where the random error zi has density function (15), β=(β1,…,βp)T, σ>0, 0<α≤1, a>0 and b>0 are unknown parameters. The parameter μi=νiTβ is the location of yi. The location parameter vector μ=(μ1,…,μn)T is represented by a linear model μ=Vβ, where V=(ν1,…,νn)T is a known model matrix.

Consider a sample (y1,ν1),…,(yn,νn) of n independent observations, where each random response is defined by yi=min{log(xi),log(ci)}. We assume non-informative censoring such that the observed lifetimes and censoring times are independent. Let F and C be the sets of individuals for which yi is the log-lifetime or log-censoring, respectively. The log-likelihood function for the vector of parameters τ=(α,a,b,σ,βT)T from model (16) has the form l(τ)=∑i∈F li(τ)+∑i∈C li(c)(τ), where li(τ)=log[f(yi)], li(c)(τ)=log[S(yi)], f(yi) is the density (13) and S(yi) is the survival function (14) of Yi. Then, the total log-likelihood function for τ reduces to

ℓτ=rlogαabσ−rlog1−1−αb+∑i∈F zi−ui+a−1∑i∈F log1−exp−ui+b−1∑i∈F log1−α1−exp−uia∑i∈C log1−α1−exp−uiab−1−αb1−1−αb
where ui=exp(zi), zi=(yi−νiTβ)∕σ and r is the number of uncensored observations (failures) and c is the number of the censored observations. The MLE τ̂ of the vector of unknown parameters can be evaluated by maximizing the log-likelihood (17). We use the statistical software R to determine the estimate τ̂.

Further, we can use the likelihood ratio (LR) statistic for comparing LGKW model with its sub-models. We consider the partition τ=(τ1T,τ2T)T, where τ1 is a subset of parameters of interest and τ2 is a subset of remaining parameters. The LR statistic for testing the null hypothesis H0:τ1=τ1(0) versus the alternative hypothesis H1:τ1≠τ1(0) is given by w=2{ℓ(τ̂)−ℓ(τ̃)}, where τ̃ and τ̂ are the estimates under the null and alternative hypotheses, respectively. The statistic w is asymptotically (as n→∞) distributed as χk2, where k is the dimension of the subset of parameters τ1 of interest.

8. APPLICATIONS

8.1. First Application

In this section, we illustrate the fitting performance of GKGa distribution by means of real data sets. We compare the fitting performance of GKGa distribution with its sub-models. The sub-models of the GKGa distribution are given as follows: (i) Gamma distribution, (ii) exponentiated Gamma distribution, (iii) extended Gamma distribution (new), (iv) Kumaraswamy-Gamma distribution.

The used data set consists of prices (×104 dollars) of 428 new vehicles for the 2004 year (Kiplinger's Personal Finance, Dec 2003) (see for details Oluyede et al. [8]). The required computations are carried out using the R software. Summary statistics of used data set are presented in Table 3.

Data set Mean Median SD γ1 γ2
Prices (×104 dollars) of 428 new vehicles 3.3 2.7 1.9 2.8 16.7
Table 3

Descriptive statistics of turbocharger failure time data set (γ1 and γ2 are pearson skewness and kurtosis coefficients, respectively).

The measures of goodness-of-fit including the–log-likelihood function evaluated at the MLEs, Anderson-Darling (A∗) and Cramer-von Mises (W∗) are calculated to compare the fitted models. In general, the smaller the values of these statistics, the better the fit to the data.

Table 4 gives the parameter estimates and their corresponding errors, the W∗ and A∗ statistics, the minus log-likelihood values and p-values. Based on Table 4, it is clear that GKGa distribution provides the overall best fit and therefore could be chosen as the most adequate model among the considered models for modeling the used data set. Here, we also applied LR tests. The LR tests can be used for comparing the GKGa distribution with its sub-models. For example, the test of H0:α=1 against H1:α≠1 is equivalent to comparing GKGa and K-Ga distributions with each other. For this test, the LR statistic can be calculated by the following relation

LR=2ℓα̂,â,b̂,λ̂,β̂−ℓ1,â∗,b̂∗,λ̂∗,β̂∗,
where â∗, b̂∗, λ̂∗ and β̂∗ are the ML estimators of a,b, λ and λ, respectively, obtained under H0. Under the regularity conditions and if H0 is assumed to be true, the LR test statistic converges in distribution to a chi square with r degrees of freedom, where r equals the difference between the number of parameters estimated under H0 and the number of parameters estimated in general, (for H0:α=1, we have r=1). Table 5 gives the LR statistics and the corresponding p-values for the first data set.

Models α a b λ β A* W* −ℓ p−νalue
Ga 1 1 1 4.071 1.242 4.308 0.646 777.719 0.035
− − − 0.267 0.086
Ex-Ga 0.005 1 681.384 4.247 0.848 1.668 0.234 758.5601 0.422
0.011 − 93.441 0.294 0.115
Exp-Ga 1 111.785 1 0.078 0.602 1.175 0.156 754.536 0.550
− 44.434 − 0.030 0.033
K-Ga 1 2.500 0.344 3.426 2.310 1.558 0.215 757.241 0.244
− 0.011 0.017 0.005 0.005
GKGa 0.005 449.042 437.736 0.016 0.404 0.433 0.047 748.677 0.916
0.024 94.829 44.201 0.040 0.063
Table 4

Parameters estimates of proposed model and other competitive models.

Models Hypotheses LR Statistic w p Value
GKGa vs Ga H0=a=b=α=1 58.084 <0.0001
GKGa vs Ex-Ga H0=α=1 19.766 <0.0001
GKGa vs Exp-Ga H0=b=α=1 11.718 0.003
GKGa vs K-Ga H0=α=1 17.128 <0.0001
Table 5

LR tests results for first data set.

Based on Table 5, we reject all the null hypotheses and conclude that the GKGa fits the used data set better than the its sub-models according to the LR test.

We also plotted the fitted pdfs of the considered models for the sake of visual comparison, in Figure 4. Figure 4(a) represents that the GKGa fits the right skewed data very well. In addition, we presented the plots of the fitted density, cumulative and survival functions as well as the probability-probability (P-P) plot for the GKGa model in Figure 4(b). These plots reveal that the GKGa distribution is a suitable model for the data.

Figure 4

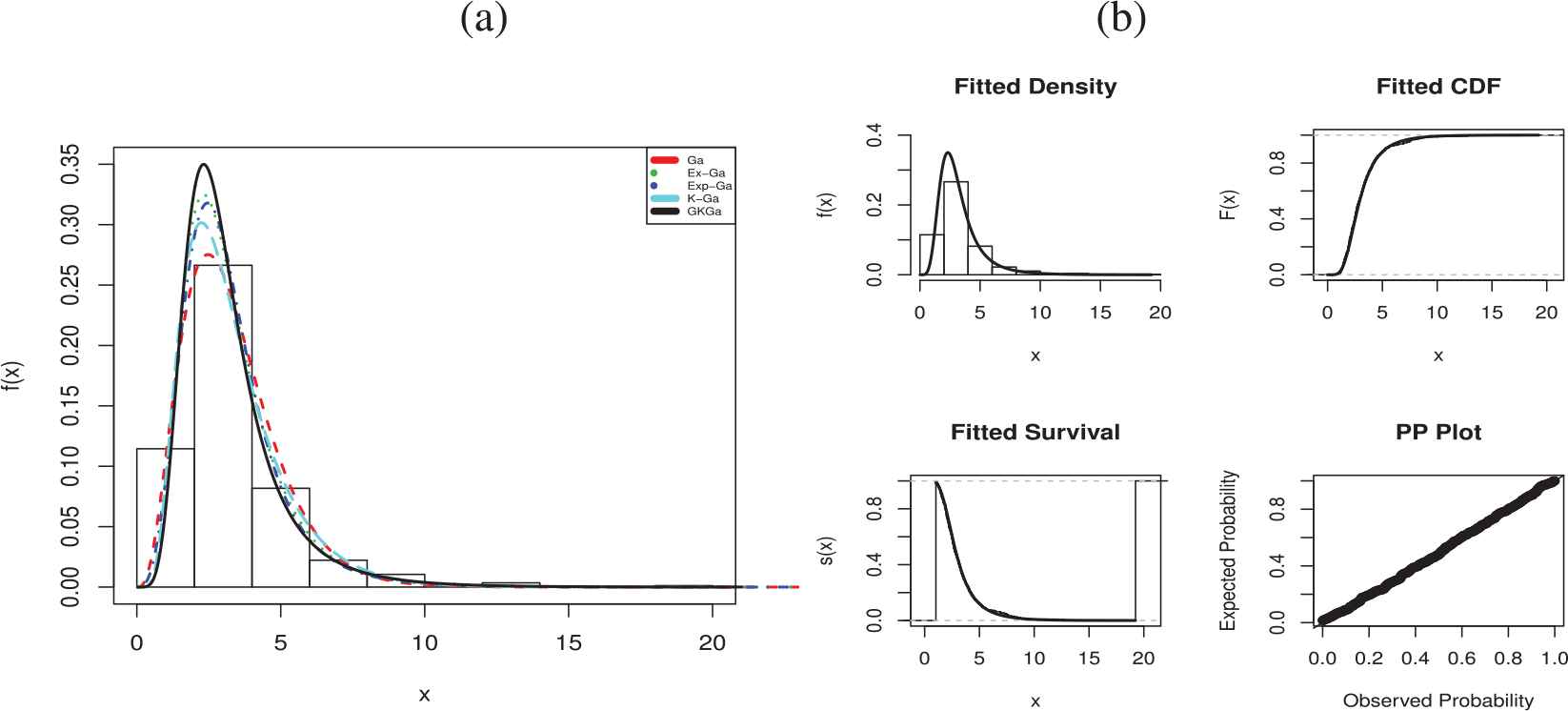
(a) Fitted densities of models and (b) fitted functions of GK-gamma (GKGa) for used data set.

8.2. Second Application

The dataset contains 100 observations on HIV+ subjects belonging to an Health Maintenance Organization(HMO). The HMO wants to evaluate the survival time of these subjects. In this hypothetical data set, subjects were enrolled from January 1, 1989 until December 31, 1991. Study follow-up then ended on December 31, 1995. This data set are reported in Hosmer and Lemeshow [9] and also can be found in R package Bolstad2. The variables involved in the study are: yi - observed survival time (in months); censi - censoring indicator (0 = alive at study end or lost to follow-up, 1 = death due to AIDS or AIDS related factors) and xi1(1=yes,0=no) represents the history of drug use.

The aim of the study is to relate the survival time (y) with the history of drug use (ν). We consider the following regression model

yi=β0+β1νi+σzi,
where yi has the LGKW density (13), for i=1,…,100. Table 6 represents the MLEs of the model parameters of the LGKW and LW regression models fitted to the current data and the log-likelihood and AIC statistics. These results indicate that the LGKW regression model has the lowest values of these statistics, and so LGKW model provides better fitting than LW model for current data. For the fitted regression models, note that β1 is marginally significant at the 1% level and then there is a significant difference between the drug user and drug non-user for the survival time.

Model α a b σ β0 β1 −ℓ AIC
LW 1 1 1 1.070 3.003 −1.051 146.437 298.875
− − − (0.088) (0.166) (0.239)
[<0.001] [<0.001]
LGKW 4.07E-09 22.383 25.742 3.675 −2.255 −0.865 140.904 293.808
(0.0001) (4.098) (4.379) (1.917) (4.393) (0.271)
[0.607] [0.001]
Table 6

MLEs of the parameters (standard errors in parentheses and p-values in [⋅]) and the log-likelihood and AIC measures.

A comparison of the LGKW regression model with LW regression model using LR statistics is performed. LR test statistic is calculated as 11.066 and corresponding p-value is 0.011. These results indicate that the LGKW model provides better fit to these data than the LW regression model.

The plots in Figure 5(a) provide the Kaplan-Meier (KM) estimate and the estimated survival functions of the LGKW regression model. There is significant difference between drug users and drug non-users survival functions. The plots of the hrf in Figure 5(b) corresponding to the survival time variable under the LGKW regression model indicate that the hrf is larger for drug non-users than drug users. Based on these plots, we conclude that the LGKW regression model provides a good fit to these data.

Figure 5

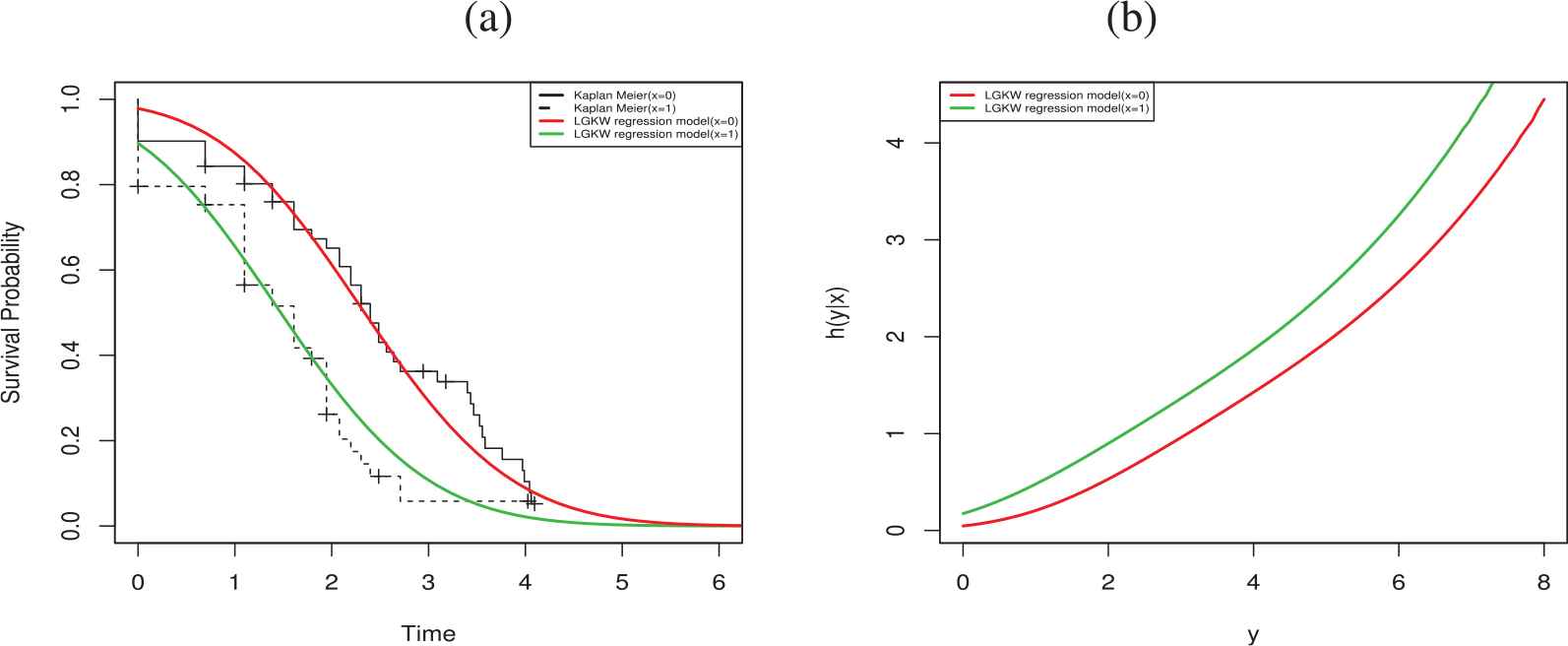
(a) Estimated survival functions and the empirical survival: :Log-generalized Kumaraswamy-Weibull (LGKW) regression model versus KM. (b) Fitted hrf using the LGKW regression model for the history of drug use.

9. CONCLUSION

We propose a new class of continuous distributions named the generalized Kumaraswamy family to extended the some classes of distributions such as Exp-G by Gupta et al. [7] and K-G by Cordeiro and de Castro [1]. We obtain some mathematical properties of proposed family including quantile function, moments, generating function, entropies, order statistics and probability weighted moments. The maximum likelihood method is used to estimate the model parameters and the performance of the maximum likelihood estimators are discussed in terms of biases, mean squared errors, coverage probability and estimated average length by means of Monte-Carlo simulation study. The usefulness of the proposed family is discussed by means of two real data applications.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

AUTHORS' CONTRIBUTIONS

All authors contributed equally to this work.

Funding Statement

This work has no fund.

ACKNOWLEDGMENTS

The authors would like to thank the Editor in Chief and two reviewers for their constructive comments which improved the final version of the paper.

REFERENCES

4.A.Z. Afify, M., Alizadeh, H.M. Yousof, G. Aryal, and M. Ahmad, Pak. J. Stat., Vol. 32, 2016, pp. 139-160.
8.B.O. Oluyede, F. Mutiso, and S. Huang, J. Data Sci., Vol. 13, 2015, pp. 281-309.
9.D.W. Hosmer and S. Lemeshow, Applied Survival Analysis: Regression Modeling of Time to Event Data, John Wiley and Sons Inc., New York, 1998.
Download article (PDF)
Next Article In Issue>
Journal
Journal of Statistical Theory and Applications
Volume-Issue
18 - 4
Pages
329 - 342
Publication Date
2019/11/20
ISSN (Online)
2214-1766
ISSN (Print)
1538-7887
DOI
10.2991/jsta.d.191030.001How to use a DOI?
Copyright
© 2019 The Authors. Published by Atlantis Press SARL.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Zohdy M. Nofal
AU  - Emrah Altun
AU  - Ahmed Z. Afify
AU  - M. Ahsanullah
PY  - 2019
DA  - 2019/11/20
TI  - The Generalized Kumaraswamy-G Family of Distributions
JO  - Journal of Statistical Theory and Applications
SP  - 329
EP  - 342
VL  - 18
IS  - 4
SN  - 2214-1766
UR  - https://doi.org/10.2991/jsta.d.191030.001
DO  - 10.2991/jsta.d.191030.001
ID  - Nofal2019
ER  -