Dynamics Analysis of Payload On-orbit Catapult Separation Based on ADAMS
- DOI
- 10.2991/jrnal.2018.5.2.6How to use a DOI?
- Keywords
- Guide mechanism; catapult separation; virtual prototype; angular velocity
- Abstract
In this paper, a catapult separation device equipped with guide mechanism is considered, and the corresponding dynamic model is descripted firstly. Then, employing the dynamic simulation software ADAMS, the virtual prototype model of the separation device is established, and the whole process of on-orbit separation is simulated. Finally, the structure parameters of the guide mechanism such as the number of roller group or distance between groups are studied. The simulation results could provide references for the optimization of the separation device.
- Copyright
- Copyright © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
On-orbit separation refers that satellite platform separates payload with a separation device, and the payload enters its preset orbit successfully1. The common schemes for on-orbit separation include pyrotechnic separation, electromagnetic separation and catapult separation. Pyrotechnic separation has security problem since the separation process with explosive material would produce large impact and interference on onboard devices; electromagnetic separation requires more power consumption, meanwhile, it's easily influenced by external magnetic field; however, catapult separation has the following advantage: simple structure, less power consumption and easy to control, therefore, the catapult separation is chosen in this paper.
Due to the deviations of compressing spring parameters, machining errors or external disturbances, the mass center of the payload is not on the resultant force in the process of catapult separation. The additional torque introduced by the eccentric separation would affect the attitude or even cause tumbling of the payload, so it is very important to study the separation dynamics of eccentric payload. Jeyakumar2 established the dynamic equations for the satellite separation system using the helical compression spring mechanism. In Jiang’s research3, characteristics of the constrained and centroid biased on-orbit satellite separation were analyzed, and then the dynamic model of the separating motion was formulated. Based on multi-body dynamic theory, Shen4 built the eccentric separation model, and simulated the dynamic during the separation by ADAMS software. Zhang5 built virtual prototype model of separation mechanism to simulate the whole process of payload on-orbit launch, and analyzed the stability of on-orbit launch considering the influence of separation mechanism error. Shu6 focused on the multi-body dynamics during separation/release, and established the simulation model based on ADAMS. The above researches stressed on dynamics analysis of tube-shape eccentric sub-satellite separation, and analyzed the influences of separation mechanism parameters on satellite platform by employing MATLAB or ADAMS platform. On basis of the previous studies, in this paper, a new type of catapult separation device equipped with guide mechanism is presented, and the influences of the guide mechanism's parameters on the payload attitude are analyzed in ADAMS/View.
2. Problem Formulation
2.1. Description of catapult separation device
As shown in Fig. 1, the catapult separation device includes driving motors, differential gear mechanism, four compression springs, the guide mechanism, a car used for loading the payload, and so on. The guide mechanism consisting of rollers plays a crucial role in restraining angular velocity of the payload. According to the general design scheme, the whole separation process can be divided into three phases as follows:
- (i)
the payload moves together with the car, in other words, they maintain relative static,
- (ii)
the car collides with the buffers in the end of whole distance, the payload moves along the guide mechanism under the effect of inertial force, and the payload is still not out of the car in this phase,
- (iii)
the payload is completely out of the guide mechanism’s constraints, that means the car and the payload move respectively.
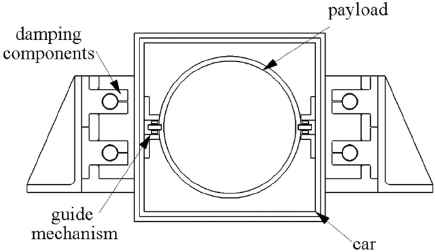
Schematic drawing of the catapult separation device
2.2. Dynamics description
During the process of catapult separation, the separation impulse is provided by release of the energy stored in the compressing springs. Based on the structure of the separation device, the force of the payload include spring force and the contact force produced by the rollers. By means of multi-body dynamics theory, the force and the moment of payload are analyzed and calculated as follows:
Based on Hertz contact theory, the nonlinear spring damping contact model is adopted to model the contact force which can be expressed as
3. Virtual Prototype Modeling
Using the ADAMS software, the virtual prototype model including the satellite platform, the payload and the catapult separation device is established as shown in Fig. 2. In general, there is a constraint relationship known as joint between two components, this model has three kinds: Fixed joint, Revolute joint, and Translational joint.
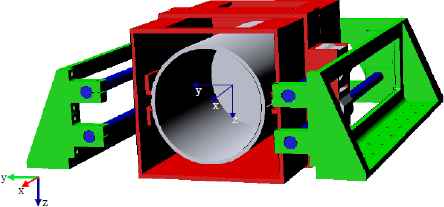
Virtual prototype model of separation system
Then, we should define force, torque, and contact for the virtual prototype model. The defined contacts are demonstrated in Table 1, calculating for which there are two methods: Restitution method and Impact method. According to the dynamics analysis in chapter 2, we adopt the Impact method in this model.
| Schedule | Rigid 1 | Rigid 2 |
|---|---|---|
| Contact 1 | car | payload |
| Contact 2 | car | buffer |
| Contact 3 | roller_11 | payload |
| Contact 4 | roller_12 | payload |
| Contact 5 | roller_21 | payload |
| Contact 6 | roller_22 | payload |
Contacts of the model
4. Simulation
The payload’s angular velocity is the main target of measuring the stability of on-orbit catapult separation. Many factors influence the separation angular velocity, including various structure parameters of the device and the motion of the satellite platform. Here, the structure parameters of the guide mechanism are discussed. By analyzing the influence rules of the parameters under different conditions, we can optimize and redesign the guide mechanism.
We assume that the initial angular velocity of the satellite platform is zero, and the orbit motion of the payload is neglected in the process. The mass of the platform is M = 500kg, the mass of the payload is m = 5kg; the stiffness coefficients of four compression springs are set as k1 = 2.43N/mm, k2 = 2.46N/mm, k3 = 2.47N/mm k4 = 2.48N/mm respectively; the spring stroke length is Δx = 90mm (the velocity of the car will be 4m/s), the gravity is neglected; and the simulation time is 0.1s, the step is 200, the lock is released at t = 0.034s, otherwise.
The guide mechanism primitively has two groups of rollers, and now we add one group of rollers between the two groups on the premise of little change of the separation velocity as shown in Fig. 3, the distance between the added group and the first group is set as l = 75mm.
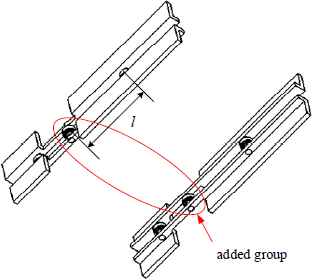
Installation of the groups of rollers
Fig. 4 shows the final roll angular velocity (rotation about x axis) decreases from 0.849°/s to 0.553°/s, the yaw angular velocity (rotation about y axis) decreases from 1.063°/s to 0.870°/s, and the pitch angular velocity (rotation about z axis) decreases from0.594°/s to 0.4°/s after adding one group of rollers. So adding groups of rollers on the premise of little change of the separation velocity could restrain the separation angular velocity.
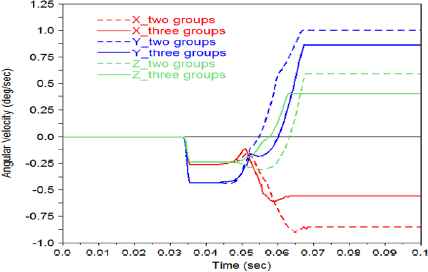
The angular velocity after adding one group of rollers
Considering the guide mechanism has three groups of rollers, we try to adjust the distance between the middle group and the first group, that is, the distance is implemented at l1 = 50mm, l2 = 35mm, respectively. The simulation results are illustrated in Fig. 5.
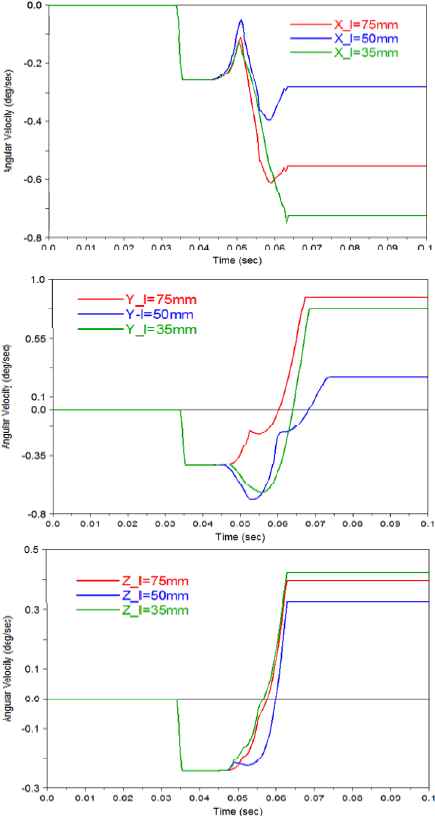
The angular velocity with different distances
When the distance decreases to 50 mm, the angular velocities including roll, yaw and pitch decrease as well (the roll angular velocity decreases to 0.280°/s, the yaw angular velocity decreases to 0.353°/s and the roll angular velocity decreases to 0.327°/s); however, if the distance continues to decrease to 35 mm, the angular velocities will increase instead.
5. Conclusion
In this paper, a new type of catapult separation device equipped with guide mechanism is considered; using the ADAMS software, the virtual prototype model is established. The simulation results show that adding one group of rollers and adjusting it to the center of the other two groups could restrain the angular velocity effectively.
Acknowledgements
This work was supported by the National Basic Research Program of China (973 Program: 2012CB821200, 2012CB821201), the NSFC (61327807, 61520106010, 61134005, 61521091).
References
Cite this article
TY - JOUR AU - Yi Li AU - Yingmin Jia AU - Jianheng Ling PY - 2018 DA - 2018/09/30 TI - Dynamics Analysis of Payload On-orbit Catapult Separation Based on ADAMS JO - Journal of Robotics, Networking and Artificial Life SP - 101 EP - 104 VL - 5 IS - 2 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.2018.5.2.6 DO - 10.2991/jrnal.2018.5.2.6 ID - Li2018 ER -
