1. Introduction

The silicon neuronal network is composed of analog and (or) digital circuits that solve the differential equations of neuronal and synaptic models. Different kinds of neuronal models have been used in silicon neuronal networks because of the trade-off between reproducibility of neuronal activities and computational efficiency. For example, Merolla et al.¹ constructed a digital silicon neuronal network comprising 1 million spiking neurons and 256 million synapses. They adopted Leaky integrate-and-fire (LIF) model that is one of the most commonly used and simple neuron models. Thomas et al.² implemented 1024-spiking neurons of Izhikevich (IZH) model³ on a field-programmable gate array (FPGA). Those LIF, expanded LIF, and IZH models are categorized as integrate-and-fire (I&F) based model which approximates a spiking process by the resetting of the state variables. The I&F-based models can be implemented resource-efficiently, but are capable of reduced reproducibility of complex neuronal activities. For example, these models assume that the amplitude of spikes is fixed, whereas the spike intensity is nonuniform in the nervous system.⁴

We have been studying qualitative neuronal models for digital as well as analog circuit implementation that satisfy both the reproducibility of neuronal activities and low computational cost.^{5, 6, 7, 8} The core idea of our qualitative-modeling-based approach is to reproduce the core mathematical structures that a wide variety of neuronal activities. In our previous studies,^{9, 10} we extended the DSSN models⁷ to support various neuronal classes; regular spiking (RS), fast spiking (FS), intrinsically bursting (IB), low-threshold spiking (LTS), elliptic bursting (EB), and parabolic bursting (PB). We also studied an automatic parameter fitting method using the differential evolution (DE) algorithm¹¹ for the RS and FS classes.¹²

In this work, we developed the method for the low-threshold spiking and intrinsically bursting classes. Parameters were optimized to reproduce waveforms of the ionic-conductance models in Ref. 13 and reduce the circuit resource requirements for implementation.

The remainder of this paper is organized as follows. Section 2 introduces our neuron model, the DE algorithm, and details of our parameter optimization procedure. The result is shown in Section 3. Section 4 summarizes this work and suggests ideas for the future.

2. Method

3. Result

We found two parameter sets with which the DSSN model reproduces the activities of the ionic-conductance models for LTS and IB classes (Fig. 1). We evaluated the similarity of the spiking patterns between the ionic-conductance model and the DSSN model by calculating some statistics while changing the stimulus intensity (Fig. 3). For the LTS class, we used C_V and L_V¹⁴ and these are explained in our previous study.¹² Our fitted model’s C_V – L_V characteristics are not completely the same as that of the reference model, but share the trend that C_V and L_V decreases as the stimulus intensity increases. For the IB class, we measured the number of spikes in the bursting duration and average firing rate after the bursting. With both models, the number of spikes in the bursting duration increases linearly as the average firing rate increases, although the exact value does not coincide completely. The similarity of these characteristics will be further estimated based on the requirements specified by the circuits’ applications.

Fig. 1.

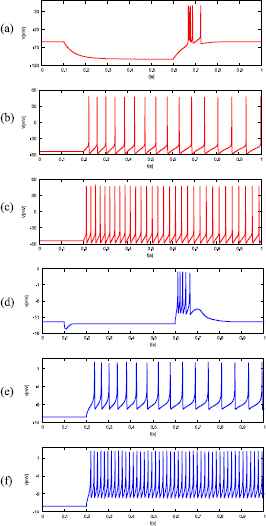
Waveforms of the ionic-conductance model (red) and the DSSN model (blue) of the LTS class in response to an inhibitory (top) and weak excitatory (middle) and strong excitatory (bottom) step stimulus input.

The results in Figs. 1, 2, and 3 were obtained by numerical integration with fixed-point operation and the Euler’s method (dt = 2⁻¹³ s) in C language. The same results are expected to be observed in the following FPGA implementation, because this condition is the same as our VHDL codes. We compiled the DSSN models for Xilinx XC7VX690T using Xilinx Vivado Design Suite. Device utilization is listed in Table 1. In the column labeled LTS (hand-fitted) and IB (hand-fitted), the resource usage for LTS and IB settings in Ref. 9 is shown. The requirement for LUTs was reduced without any loss of the reproducibility of the neuronal activities.

Fig. 2.

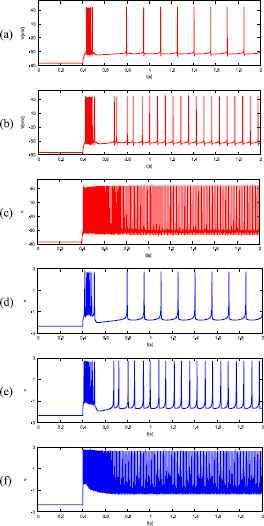
Waveforms of the ionic-conductance model (red) and the DSSN model (blue) of the IB class in response to a weak (top) and middle (middle) and strong (bottom) excitatory step stimulus input.

Fig. 3.

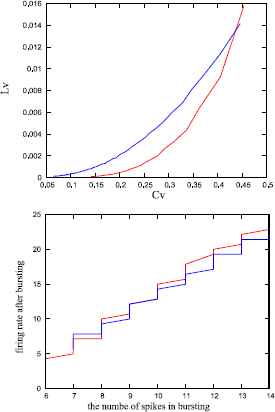
Statistical properties of the ionic-conductance model (red) and the DSSN model (blue). In the LTS mode (left), the x–axis and y-axis are C_V and L_V. In the IB mode (right), x-axis corresponds to the number of spikes in the bursting and y-axis corresponds firing rate after the bursting.

Table 1:

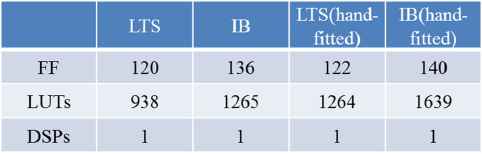
Device Utilization.

4. Conclusion

In this work, we extended the parameter optimization method for the DSSN model in the LTS and IB class modes. These classes have complex mathematical structures of the fast subsystem, thus we carefully designed our fitting procedure in order to reproduce important structures in these classes. We could find parameter sets with which the DSSN model reproduces the characteristics activities of LTS and IB classes using average-power PC (a Xeon E5-2667 CPU with a NVIDIA P100 GPU). Cost functions f_bx were introduced to reduce the necessary circuit size. We confirmed that the DSSN model with determined parameter set can precisely reproduce the ionic conductance model in C simulation, and the necessary circuit size was simulated by Xilinx Vivado Design Suite. In our future work, we will apply our silicon neuronal networks to the spike pattern recognition.¹⁵

Acknowledgement

This work was partially supported by JSPS SAKURA Program and JST PRESTO and CREST