Design and Development of a Constant-Temperature Reservoir for a Database-Driven Smart Cultivation System
- DOI
- 10.2991/jrnal.2018.5.1.7How to use a DOI?
- Keywords
- cultivation System; temperature control; database-driven control; nonlinear control
- Abstract
Decreasing the number of people working in the agriculture sector is a serious problem in Japan. Production of agricultural products in a plant factory is one of the solutions to the above problem. However, setting optimal environmental conditions is difficult owing to the nonlinearity of the system. This research aims for the realization of a smart cultivation system using a database-driven (DD) technique. In this paper, a pilot scale constant-temperature reservoir with a nonlinearity regarding the Peltier device was developed, and its derivative equations were derived. Moreover, a DD controller was designed for the system, and the simulations demonstrate that the proposed control system could control the temperature to a wide desired temperature range.
- Copyright
- Copyright © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
In recent years, there has been a growing interest toward and requirement of domestic and pesticide-free production of agricultural products in Japan. However, the decrease in the agricultural workforce has not been abated. Owing to the above situation, a plant factory1, 2 that could automate the production process of various agricultural products and would be able to safely and stably produce food products has garnered much attention. The production schedule of a plant factory can be controlled by manipulating its environmental conditions such as temperature, humidity, and CO2 concentration. Although the environmental control system, which is a cultivation system, must be designed to optimize the above variables, a uniform system design method that can deal with various kinds of plants has not yet been established. Moreover, the controlled objects have strong nonlinearity. Thus, it is difficult to manipulate them using linear controllers such as fixed PID controllers3, which are applied to more than 90% of industrial systems. In addition, it may be difficult to maintain ideal environmental conditions of a cultivation system using such a controller due to the changing environment around the factory and the deterioration of the aging equipment. Because of the above situation, this study considers the establishment of a smart cultivation system based on a database-driven (DD) control system design-method4 that utilizes a database including many previous operational data. According to the method, the controlled parameters can be adaptively tuned to correspond to the nonlinearities and changes in the environmental conditions of the controlled object. In this research, a pilot scale constant-temperature reservoir for a cultivation system is developed. In this system, a Peltier device, which is one of the thermoelectric conversion devices, is implemented to control the temperature in the reservoir. In the Peltier device, by supplying current to the device, one side exhausts the heat and the other side absorbs the heat that corresponds to the amount of the current. Moreover, the exhaust and absorption surface of the heat can be switched by changing the direction of the current. However, the amount of generated heat follows the square of the amount of the current, thus a linear controller with fixed control parameters does not maintain a good control performance due to the nonlinearity. In this study, a DD temperature controller is designed and applied to the nonlinear system. This method is expected to make the temperature follow a wide range of temperature references compared with a fixed PID controller. To verify the effectiveness of the method, the derivative equations of the system are derived and a mathematical model is realized by MATLAB/Simulink. This study is organized as follows. In Section 2, the pilot scale constant-temperature reservoir and its mathematical model is explained. In Section 3, the control results of the fixed PID and the DD controller are shown. Finally, Section 4 summarizes the research findings.
2. Constant-Temperature Reservoir Design
The appearance of the constant-temperature reservoir is shown in Fig. 1. The schematic and system parameters are shown in Fig. 2 and Table 1, respectively. The specific values of the system parameters are identified by the genetic algorithm5.

Appearance of a constant-temperature reservoir.

Schematic of a constant-temperature reservoir.
| Variable name | Explanation | Value |
|---|---|---|
| RP | Resistance of Peltier device | 3.85 |
| λP | Thermal conductivity of Peltier device | 10.0 |
| πP | Peltier coefficient | 1.00 |
| αP | Proportionality constant for TPh | 5.00 |
| RAB | Thermal resistance | 0.83 |
| CAl | Thermal capacity | 5.00 |
| RBox | Thermal resistance | 39211 |
| CBox | Thermal capacity | 994.6 |
System parameters.
2.1. Constant-Temperature Reservoir
A Peltier device is implemented on the system’s background and temperature and humidity sensors are placed on the inside of the wall. Moreover, full color LEDs for growing plants are placed on the ceiling. The Arduino is utilized as the controller, which can manipulate the amount of current from the power supply by changing the duty ratio of the PWM output voltage of the controller.
2.2. Modeling
In this section, the following couple of heat balance relationships are derived:
- (1)
Peltier device – Aluminum block.
- (2)
Aluminum block – Space of constant-temperature reservoir.
A simulator based on these heat balance models is constructed by using MATLAB/Simulink.
2.1.1. Heat balance between Peltier device and aluminum block
The derivative equation regarding the time variation of TAl(t) is given as follows:
2.1.2. Heat balance between aluminum block and Space of constant-temperature reservoir
The derivative equation related into the time variation of TBox(t) is given as follows:

Static property of the simulation model.
3. Application of DD Control Technique
The temperature of the constant-temperature reservoir must be controlled properly to produce a variety of plants. In this work, the DD control technique is applied to control the temperature. In the DD controller design scheme, an initial database is required. Thus, to generate an initial database, a fixed PID controller is applied to the system and its operation data is stored into a database.
3.1. Control result by Fixed PID controller
The initial PID parameters are obtained based on model munching. First, it is assumed that the controlled object can be approximated as the following first-order system with a time delay around an equilibrium point:

Control results obtained by the fixed PID controller.
3.2. Control result by DD-PID controller
The control results in Fig. 4 and PID gains are stored into a database, and a DD controller is designed according to the work of Yamamoto et al.4. The control results using the DD controller are shown in Fig. 5, and the trajectories of the PID gains are shown in Fig. 6. In this simulation, the rise time is set to σ = 210 s, which is faster than the fixed I-PD controller design. The results demonstrate that good control performance is obtained by adaptively tuning the PID gains based on the DD control technique.
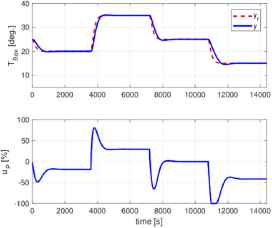
Control results obtained by the DD-PID controller.
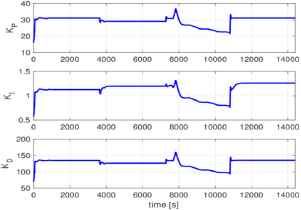
Trajectories of PID gains corresponding to Fig. 5.
4. Conclusions
In this study, a constant-temperature reservoir was developed to establish a smart cultivation system based on the DD technique. The mathematical model based on the principal of heat balance was derived and a simulator was constructed using MATLAB/Simulink. The DD controller was also designed and its effectiveness was verified using the simulation model. In a future study, the control system will be implemented to the real system and the structure of a smart cultivation system will be designed. The stability analysis of the closed-loop system will also be considered as a future study.
References
Cite this article
TY - JOUR AU - Shin Wakitani AU - Sneha Sharma AU - Toru Yamamoto PY - 2018 DA - 2018/06/30 TI - Design and Development of a Constant-Temperature Reservoir for a Database-Driven Smart Cultivation System JO - Journal of Robotics, Networking and Artificial Life SP - 27 EP - 31 VL - 5 IS - 1 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.2018.5.1.7 DO - 10.2991/jrnal.2018.5.1.7 ID - Wakitani2018 ER -
