1. INTRODUCTION

Data-driven control schemes have been proposed for directly designing a controller using a set of experimental data. Virtual Reference Feedback Tuning (VRFT) [1] and Fictitious Reference Iterative Tuning (FRIT) [2] have been proposed as data-driven control schemes. According to these schemes, control parameters can be directly calculated using a set of experimental data. However, VRFT and FRIT work well for only linear time-invariant systems, and it is difficult to obtain good control performance for linear time-varying systems.

Meanwhile, the effectiveness of the deep and machine learning have been demonstrated in the field of image recognition. The ensemble learning such as random forest [3] and adaptive boosting [4] is a machine learning scheme, and it has been proposed to improve the accuracy of prediction by using multiple learners.

This paper proposes a design scheme of data-driven controllers using ensemble learning and VRFT for linear time-varying systems. Specifically, a linear time-invariant system is first divided into some linear systems by applying ensemble learning based on decision tree learning. Second, VRFT is applied to each divided linear system for obtaining multiple linear controllers.

2. DESIGN OF DATA-DRIVEN CONTROLLER USING ENSEMBLE LEARNING

Figure 1 shows the schematic figure of the proposed data-driven control system where multiple controllers (controller-1, controller-2,…, controller-n) are designed using ensemble learning using the initial closed-loop data. First, the closed-loop data is divided into some linear time-invariant systems based on time t (t₁, t₂,…, t_n−1). Next, control parameters are calculated using VRFT for each divided data (Divided data-1, Divided data-2, …, Divided data-n).

Figure 1

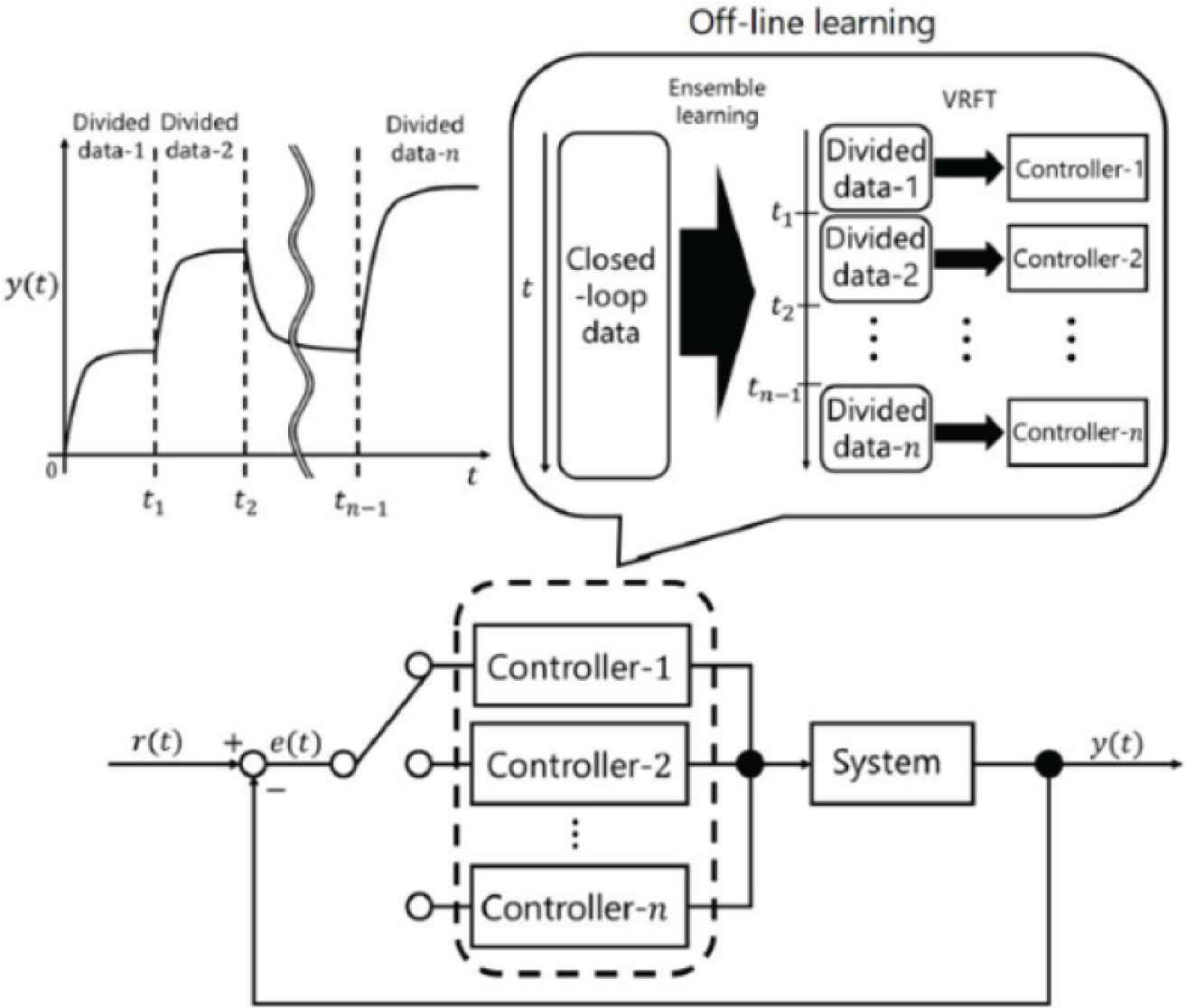
Schematic figure of the proposed control system.

2.1. Virtual Reference Feedback Tuning

Figure 2 shows the block diagram of VRFT. P(z⁻¹) is a system plant and C(z⁻¹, θ) shows the controller. θ is a control parameters. The optimization problem is adjusting θ so that closed-loop transfer function W(z⁻¹) closed to the following desired reference model G_m(z⁻¹) [5].

Gm(z−1)=z−1T(1)T(z−1) (1)

T(z−1)=1+t1z−1+t2z−2, (2)

where

{t1=−2exp(−ρ2μ)cos(4μ−12μρ)t2=exp(−ρμ)ρ=Tsσμ=0.25(1−δ)+0.51δ. (3)

T_s is the sampling time, σ and δ are the user-specified parameters related to the rise characteristic and attenuation characteristic of control system.

Figure 2

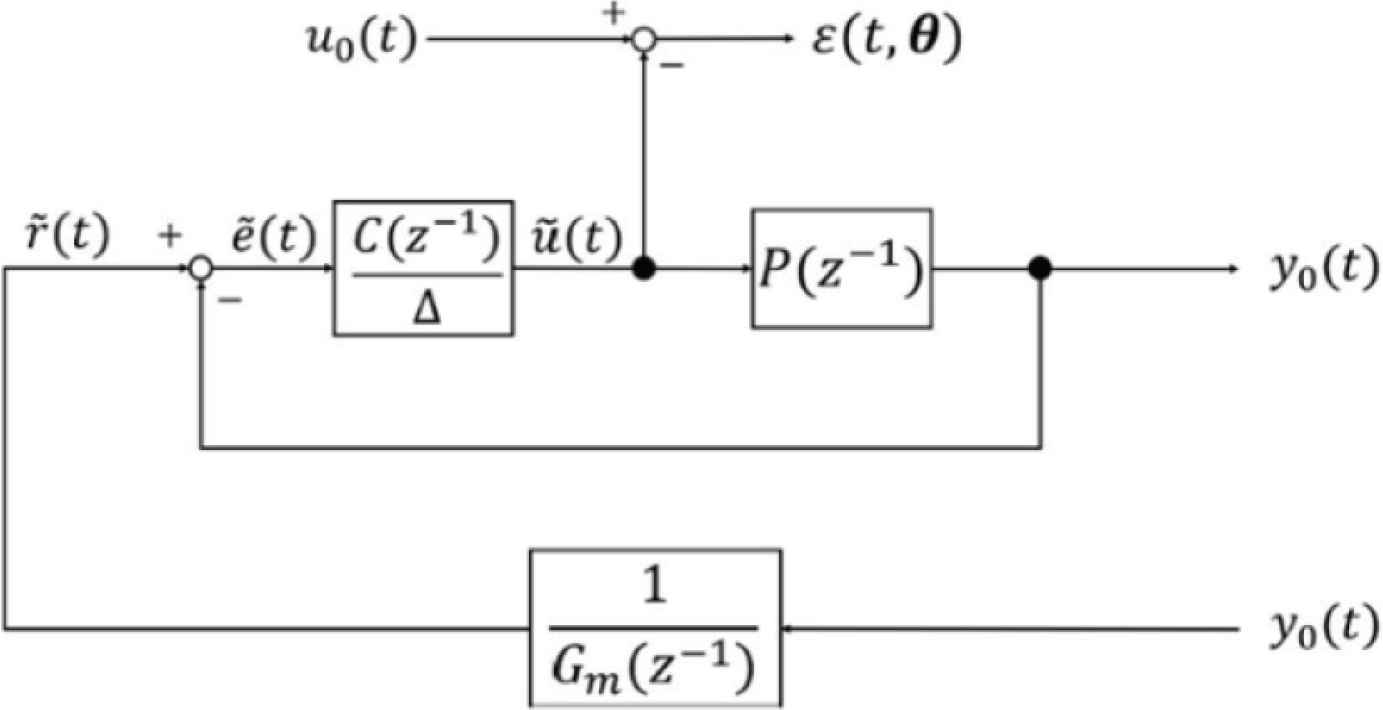
Block diagram of VRFT.

In order to match W(z⁻¹) to G_m(z⁻¹), one-shot experimental input u₀(t) and output y₀(t) is obtained. Next, a pseudo reference input r˜(t) is calculated as follows:

r˜(t)=1Gm(z−1)y0(t). (4)

The output u˜(t) is denoted as Equation (5).

u˜(t)=C(z−1,θ)Δe˜(t) (5)

e˜(t)=r˜(t)−y0(t) (6)

The following equation denotes the objective function J.

J=12∑t=1N{ε(t,θ)}2 (7)

ε(t,θ)=u0(t)−u˜(t) (8)

In this paper, I − P controller is used and the control parameter θ which minimizes the evaluation function J. From Figure 2, u˜(t) becomes given by

u˜(t)=−KPy0(t)+KIe˜(t)Δ (9)

By putting e˜(t)/Δ=x(t) , Equation (9) is rewritten as follows:

u˜(t)=−KPy0(t)+KIx(t)=θφ(t) (10)

Here, the following equations denote θ and φ(t).

θ=[KPKI]T (11)

φ(t)=[−y0(t)x(t)] (12)

The control parameter θ^* which minimizes the objective function J is obtained as Equation (13).

θ*=(ΦTΦ)−1ΦTU (13)

Φ=[φ(1)φ(2)⋯φ(N)]T (14)

U=[u0(1)u0(2)…u0(N)]T (15)

2.2. Design of Learner to Divide Closed-loop Data

In this paper, a learner is designed to divide closed-loop data into n systems in Figure 3 is designed. Decision tree learning is a scheme of assigning a data set allocated to a parent node to a child node according to a split function h^* and creating a decision tree such as Figure 4. The split function h^* is obtained as follows:

h*=arg max I (16)

I is an evaluation function showing the degree of variation of the class in the child node which divided the parent node. Based on the division scheme of the decision tree, the optimum time to split closed-loop data t*(t1*,t2*,⋯,tn−1*) is obtained using the evaluation function I as follows:

t*=arg max I(t) (17)

Here, the evaluation function I is defined as follows:

I(t)=−∑k=1nJk* (18)

Jk* is the minimum value in Equation (7) of the k^th system obtained by dividing the closed-loop data at time t.

Figure 3

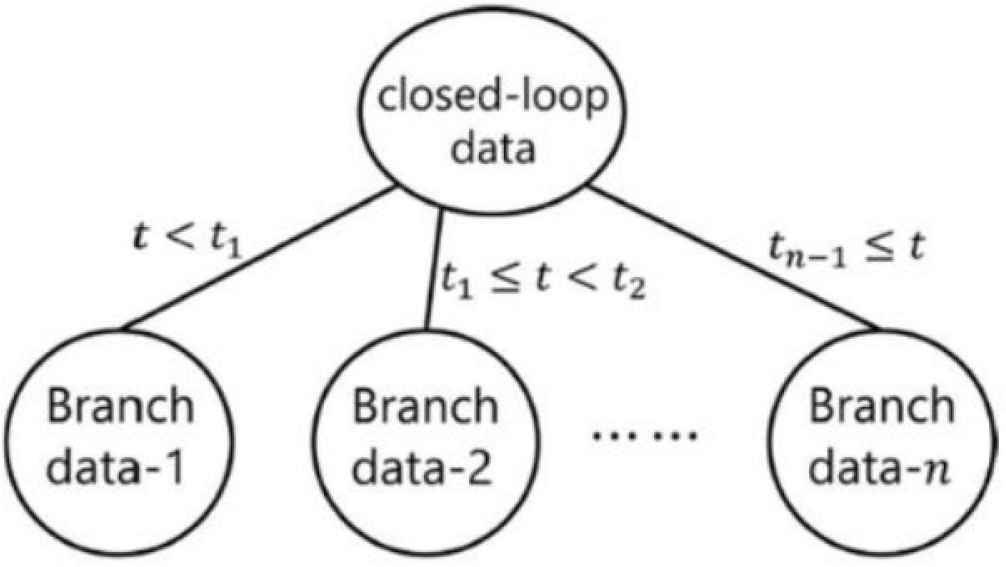
Learning instrument.

Figure 4

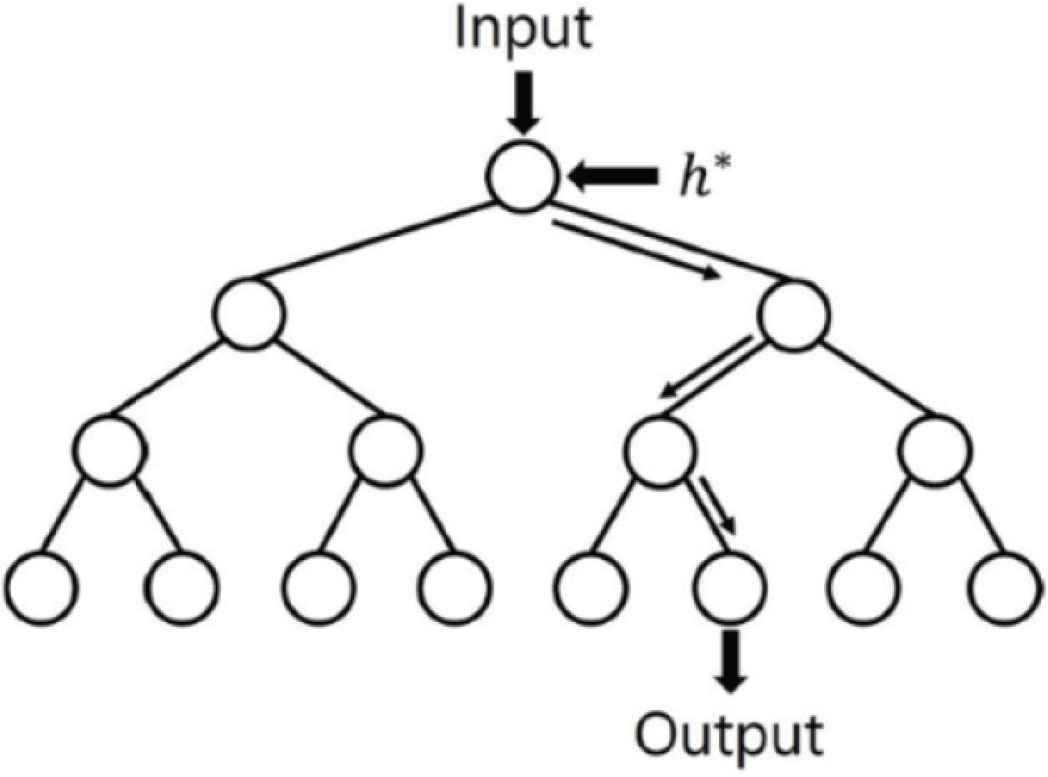
Decision tree.

2.2.1. Ensemble learning

Ensemble learning is a scheme of integrating multiple learners to generate one learner. If the accuracy of each learner is higher than 50%, it is known that higher accuracy is achieved than one learner since the learner that estimates erroneously becomes a minority.

In this paper, ‘fminsearch.m’ in MATLAB & Simulink Ver. 9.4.0813654 (R2018a), Optimization Toolbox is used to find t^*.

3. NUMERICAL EXAMPLE

3.2. Simulation Result

The control result with fixed PI gains which are calculated by VRFT is shown in Figure 5. PI gains are calculated as follows:

KP=−0.45, KI=0.10 (25)

K_P is negative gain because the system has three characteristics of Equation (22). In Figure 5, the overshoot has occurred on the output with fixed PI gains and good control results are not obtained. The sum of squared errors is 708.7 in Table 1.

Figure 5

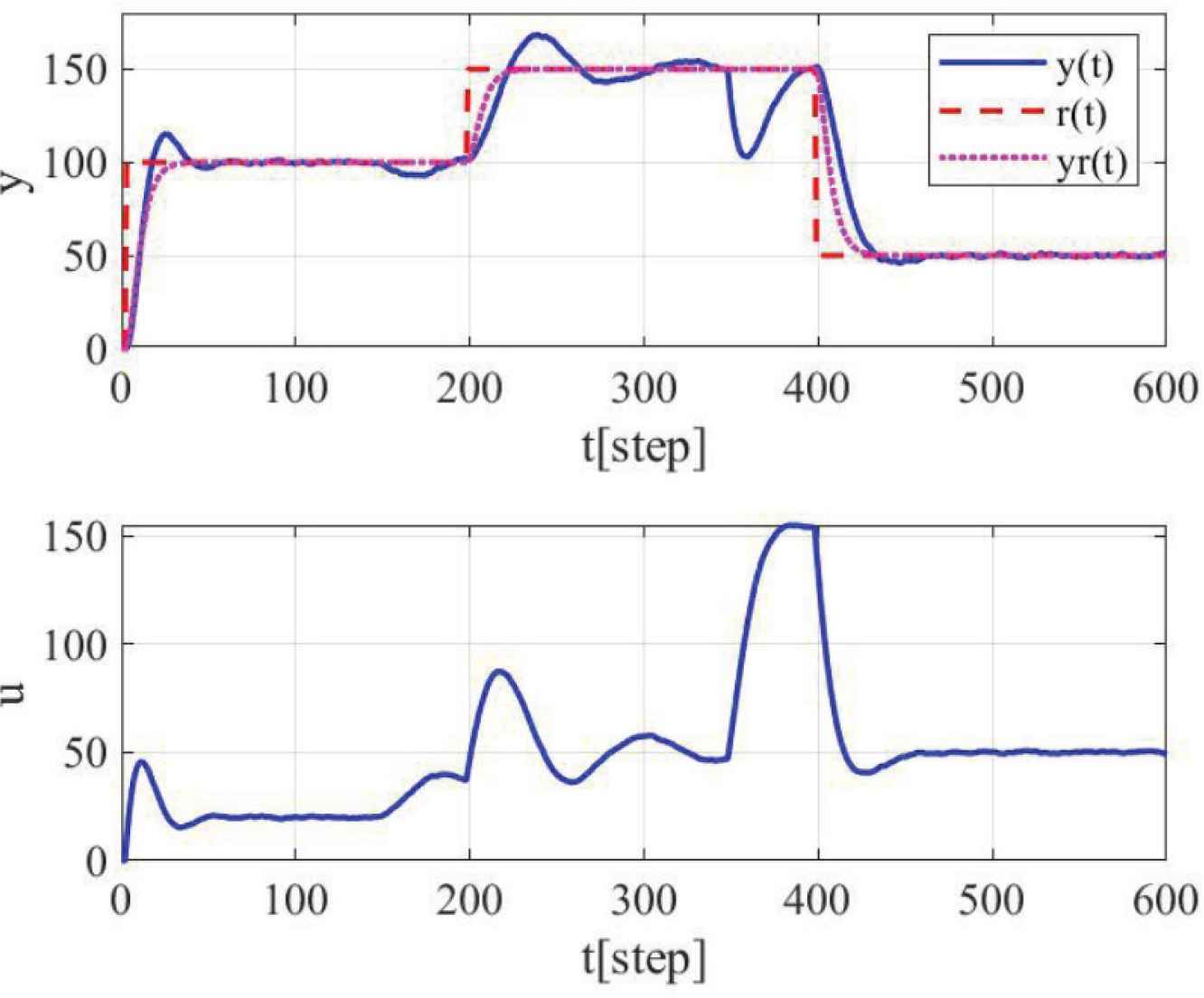
Control results using the fixed PI controller.

	Σ e(t)2
Conventional scheme (Figure 5)	708.7
Proposed scheme (Figure 6)	653.9

Table 1

Sum of squared errors

Figure 6

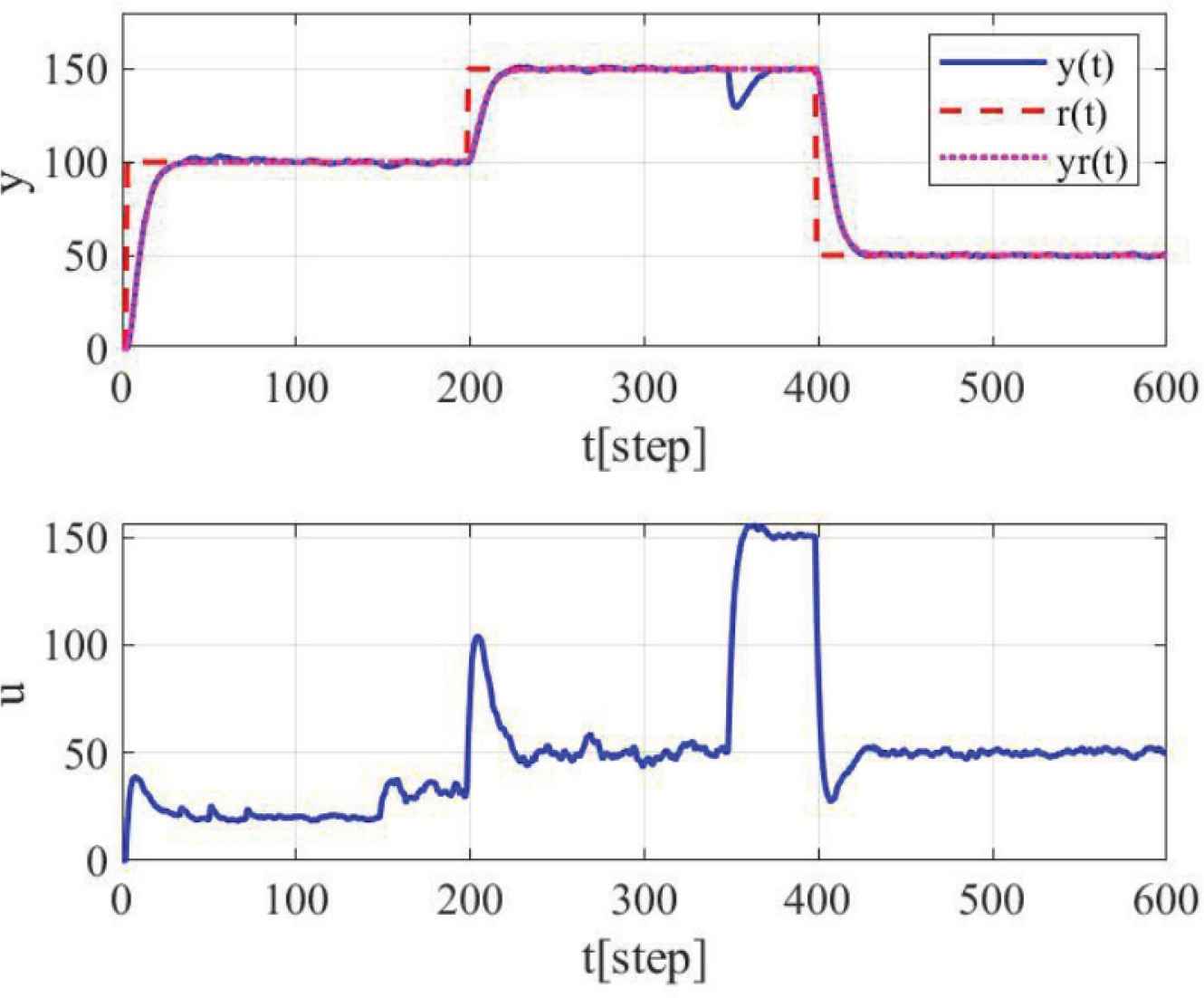
Control results using the proposed scheme.

Figure 6 shows the control result applying the proposed scheme. Here, the number of weak learners is 10. Figures 7 and 8 respectively show the estimation result of the system change step in the weak learners and the transition of PI gains in the proposed scheme. Figure 6 shows that good control result can be obtained using the proposed scheme. In addition, Figures 7 and 8 show that the system change step is estimated accurately and PI gains are changed at the proper timing. Finally, the sum of squared errors is 653.9 in Table 1, and the proposed scheme is better than the conventional scheme.

Figure 7

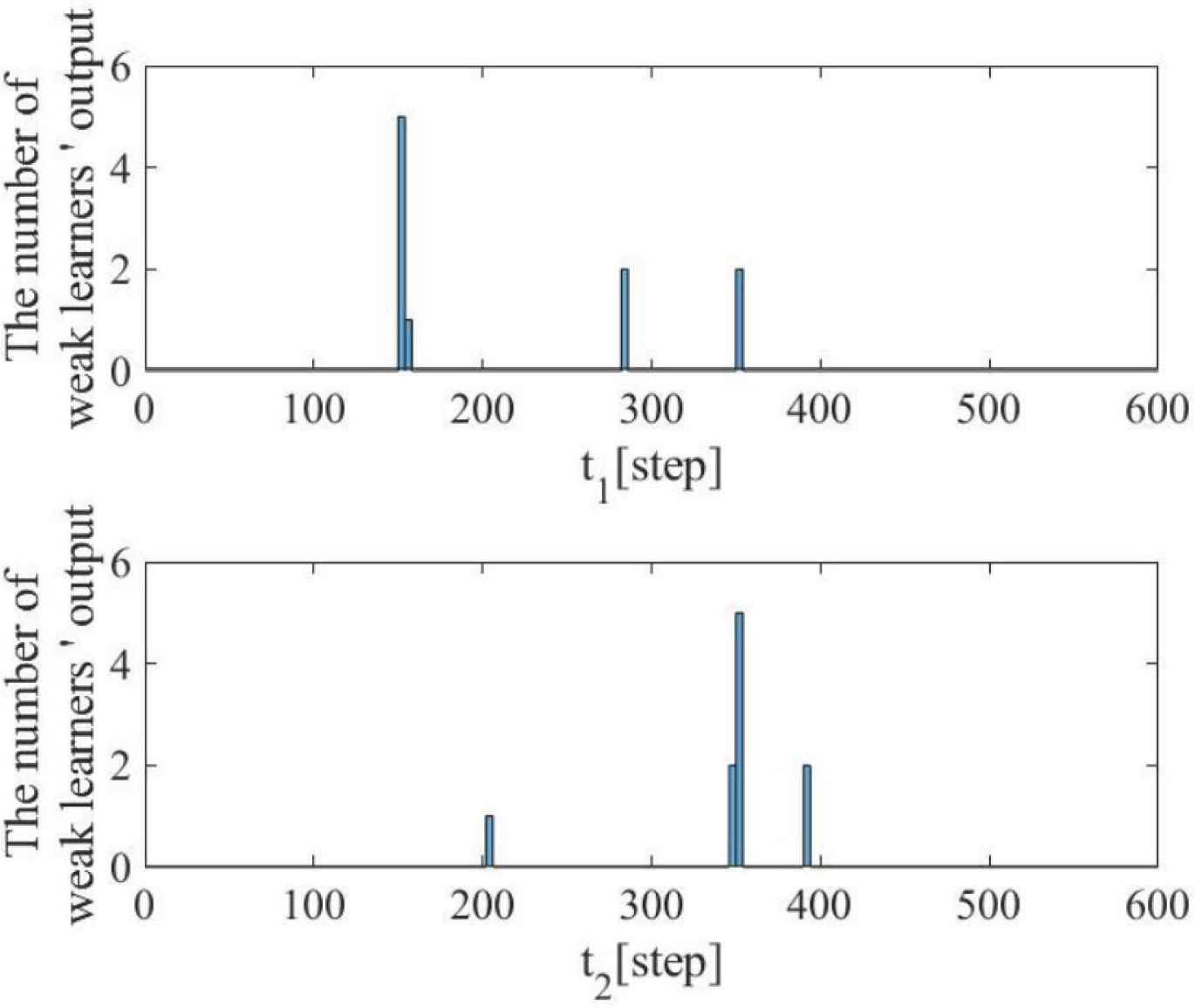
Estimation result of ensemble learning.

Figure 8

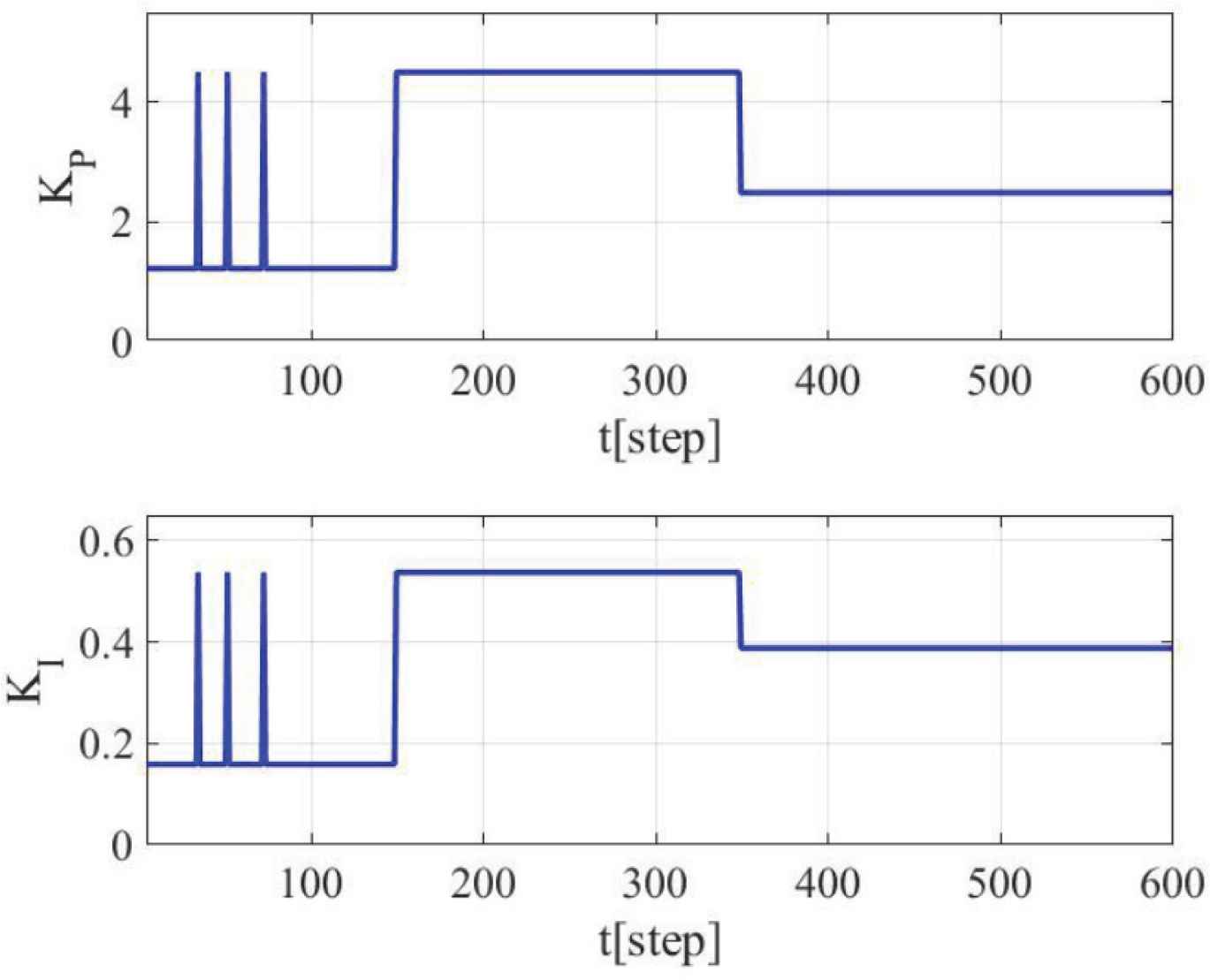
Trajectories of PI gains.

4. CONCLUSION

In this paper, a new control scheme has been proposed. It is a scheme of dividing a linear time-varying system into multiple linear time-invariant systems and applying VRFT to calculate multiple linear controllers. In the numerical example, the effectiveness of the proposed scheme has been shown.

In the future works, it is necessary to optimize the number of divisions for an unknown system. In addition, the least squares method is susceptible to noises other than normal distribution. Therefore, further consideration is needed such as incorporating bagging [6] to suppress the effects of noise.

CONFLICTS OF INTEREST

The authors declare they have no conflicts of interest.

AUTHORS INTRODUCTION

Dr. Takuya Kinoshita

He received his B.Eng., M.Eng. and D.Eng. from Hiroshima University in Japan in 2013, 2015 and 2017, respectively. He was postdoctoral fellow of JSPS (Japan Society for the Promotion of Science) in 2017. He is currently an Assistant Professor with the Department of System Cybernetics, Graduate School of Engineering, Hiroshima University, Japan. His research interests are performance driven control.

Mr. Yuma Morota

He received his B.Eng. From Hiroshima University in Japan in 2019. He is currently a Master course student in Hiroshima University, Japan.

Prof. Toru Yamamoto

He received the B.Eng. and M.Eng. degrees from the University of Tokushima, Tokushima, Japan, in 1984 and 1987, respectively, and the D.Eng. degree from Osaka University, Osaka, Japan, in 1994. He is currently a Professor with the Department of System Cybernetics, Graduate School of Engineering, Hiroshima University, Japan. He was a Visiting Researcher with the Department of Mathematical Engineering and Information Physics, University of Tokyo, Tokyo, Japan, in 1991. He was an Overseas Research Fellow of the Japan Society for Promotion of Science with the University of Alberta for 6 months in 2006. His current research interests are in the area of data-driven control, and process control. He was the recipient of the Commendation for Science and Technology by the Minister of Education, Culture, Sports and Technology in 2009.