Neuromorphic Computing in Autoassociative Memory with a Regular Spiking Neuron Model
- DOI
- 10.2991/jrnal.k.200512.013How to use a DOI?
- Keywords
- Spiking neural network; associative memory; DSSN model; spike frequency adaptation
- Abstract
Digital Spiking Silicon Neuron (DSSN) model is a qualitative neuron model specifically designed for efficient digital circuit implementation which exhibits high biological plausibility. In this study we analyzed the behavior of an autoassociative memory composed of 3-variable DSSN model which has a slow negative feedback variable that models the effect of slow ionic currents responsible for Spike Frequency Adaptation (SFA). We observed the network dynamics by altering the strength of SFA which is known to be dependent on Acetylcholine volume, together with the magnitude of neuronal interaction. By altering these parameters, we obtained various pattern retrieval dynamics, such as chaotic transitions within stored patterns or stable and high retrieval performance. In the end, we discuss potential applications of the obtained results for neuromorphic computing.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Neuromorphic computing is an attempt to realize a computing architecture capable of complex and robust calculations with low power consumption, which is designed by either imitating or inspired by the information processing mechanisms in the nervous system.
Unlike the conventional von Neumann computer architecture in which CPU and memory units exist separately, the neuromorphic hardware generally has highly distributed computation and memory units. Such a massively parallelized computation which overcomes the von Neumann bottleneck is expected to reduce overall energy consumption.
Silicon Neuronal Networks (SiNNs) are a neuromorphic hardware that attempt to reproduce the electrophysiological activities in the nervous system by electronic circuits. Models of neurons, synaptic activities and designs of underlying algorithms are crucial factors as the components in the SiNNs. Many neuron models have been proposed for reproducing various traits of neurons. However, they generally undergo the problem of trade-off between implementation cost and biological plausibility [1].
Digital Spiking Silicon Neuron (DSSN) model is a qualitative neuron model which reproduces dynamical structure in various neuronal firing activities and is designed to be implemented efficiently on digital circuit [2].
As a fundamental model of neuromorphic computation, an all-to-all connected network composed of DSSN model has been implemented and autoassociative task was performed [3]. The network retrieved a stored pattern given corresponding corrupted input patterns, and its performance varied greatly on each neuron’s parameters. It was shown that the performance is dependent on the class of the neuron model (Class 1 and 2 in Hodgkin’s Classification).
In our study we adopt the equivalent system, however, we incorporate Regular Spiking class for each neuron. Regular Spiking class exhibit Spike Frequency Adaptation (SFA) which is a convergence of firing frequency from high value to a low value given a step current with sufficiently large magnitude.
Moreover, the strength of SFA is known to be reduced by cholinergic modulation [4] and it has been modeled on network of Hodgkin Huxley type neuron model [5,6]. We aim to apply and utilize the modulatory effect for neuromorphic computing. For this purpose, we studied network dynamics by altering corresponding parameters of the DSSN model.
2. NEURON AND SYNAPSE MODEL
Two variables in the DSSN model, membrane potential v and a variable n that represents a group of ion channels, are responsible for generating neuronal spikes.
Spike frequency adaptation is reproduced by introducing an additional slow negative feedback variable q, which results to 3-variable DSSN model [7]. For simplicity, we adopt the following 3-variable DSSN model with linear q-nullcline [7] instead of the nonlinear q-nullcline model [8].
Parameter α controls strength of SFA, which is defined as the difference of Inter-spike-Interval (ISI) between the initial and the converged state. When α is low, the effect of SFA is strong (see Figure 1). Since SFA is known to be reduced during cholinergic modulation, magnitude of α can be mapped to concentration of Acetylcholine during modulation.
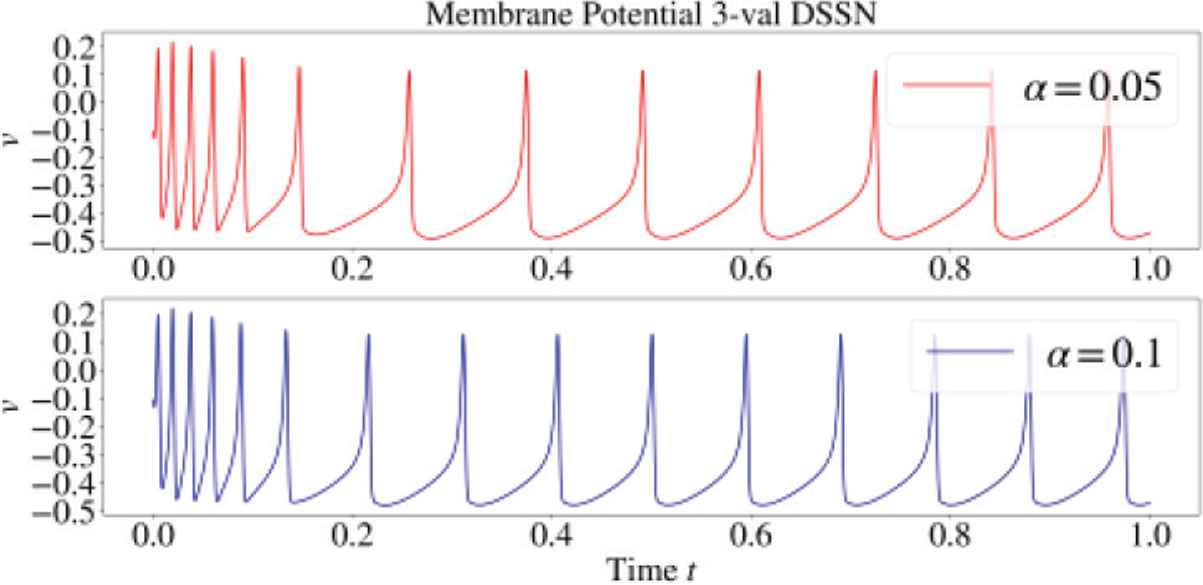
Spike frequency adaptation observed in DSSN model for α = 0.05 (Top) and 0.1 (Bottom).
Synaptic current of each neuron is modeled as,
3. NETWORK CONFIGURATION AND METHOD
Our network model is an all-to-all connected network of 256 neurons (3-variable DSSN model), and synaptic efficacy in each synapse is given by synaptic weight matrix W. External input to ith neuron is given as,
Four mutually orthogonal patterns (Figure 2a) were stored in the network by configuring synaptic weight matrix W by the following correlation rule,
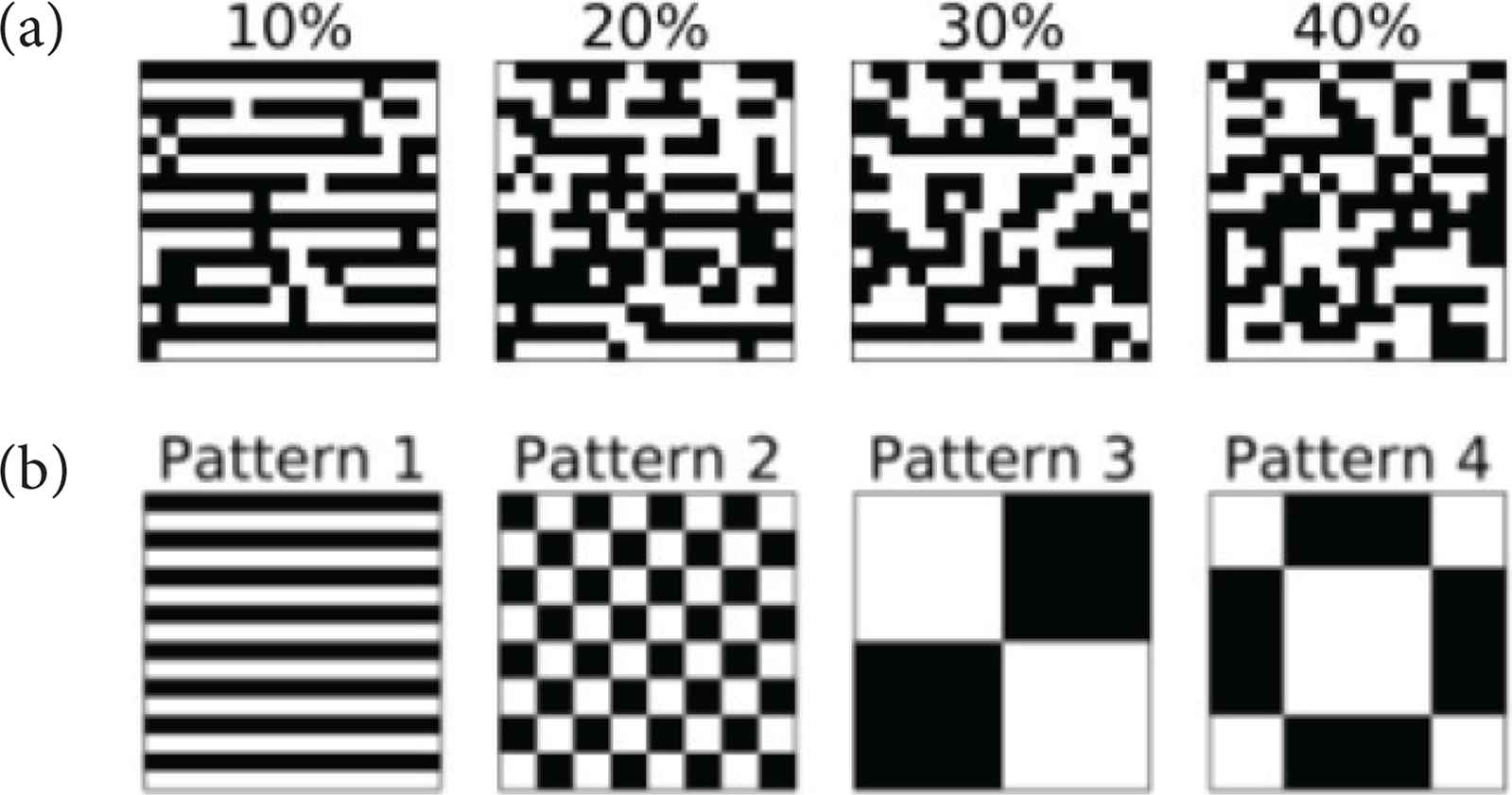
(a) Stored patterns. (b) Input data (based on Pattern 1).
The autoassociative task is performed as follows: First, we initialized the network state with corrupted input data by injecting step current Iext = 0.15 for 0.5 s (1334 timesteps) to the neurons that encode black pixel. Then, we stimulated all the neurons with Iext = 0.15 to evoke repetitive neuronal activity.
We evaluated the network state by introducing Phase Synchronization Index (PSI) which quantifies the level of synchronization, and an overlap index Mu which quantifies the similarity between firing times of every neuron and uth stored pattern. Based on the firing phase in the repetitive firing activity, PSI and overlap between the network output is computed by,
4. SIMULATION RESULTS
4.1. Weak Neuronal Interaction
We obtained stable overlap dynamics and high retrieval performance at the weak neuronal interaction region (c = 0.005). Figure 3 shows a successful retrieval process of Pattern 1. Figure 4 shows the retrieval performance evaluated over 100 trials for each value of α. Each trial was performed until t = 10. For α = 0.05 and 0.1, the successful retrieval rate keeps higher than 90% when the error rate is equal to 30% or less, which is comparable with network of class 2 neurons [3].
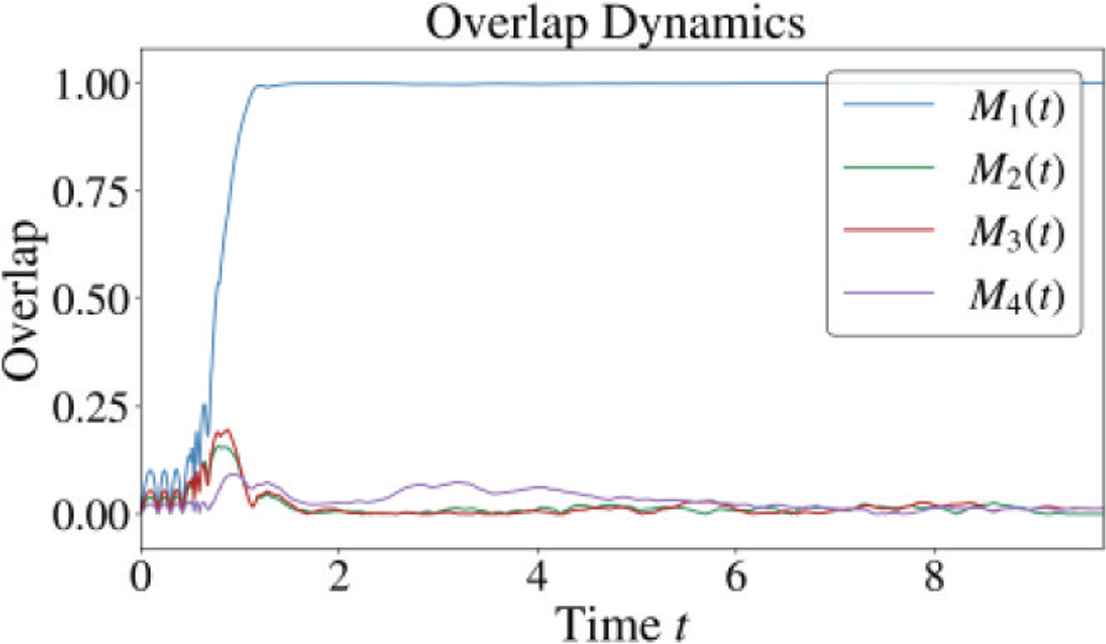
Overlap dynamics in a successful retrieval process.
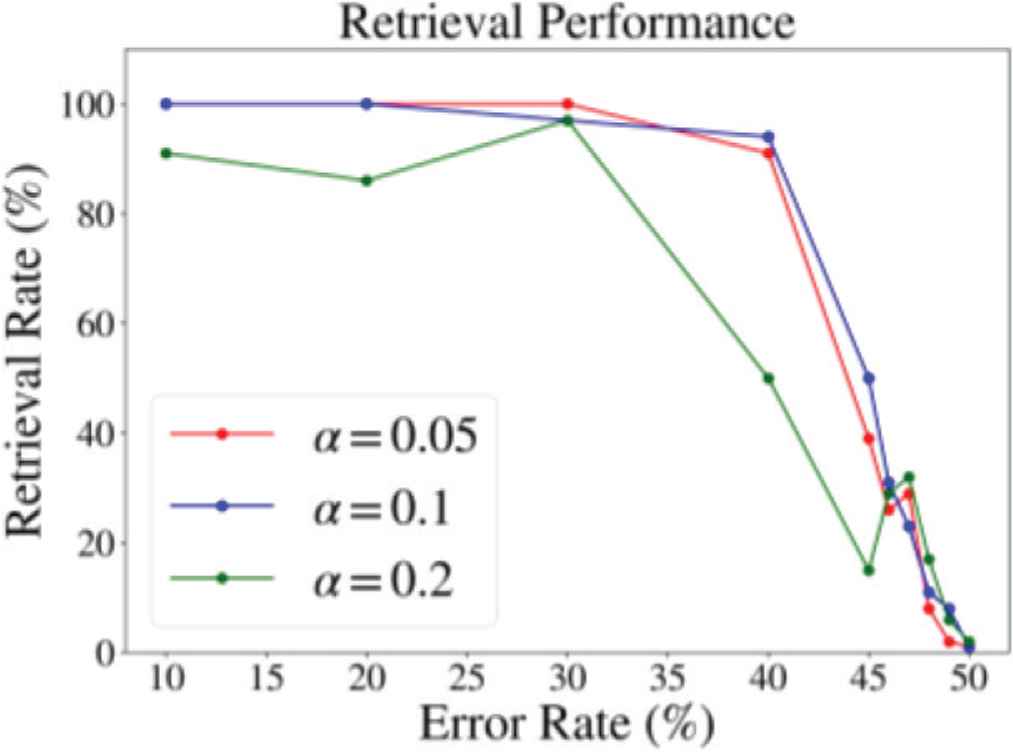
Retrieval performance. x-axis shows error rate of the input pattern. y-axis is the percentage of successful retrieval. Successful retrieval was defined when PSI and overlap of corresponding input pattern exceeded 0.9.
The superiority of retrieval performance can be reasoned by biphasic (Type 2) Phase Response Curve (PRC) [9] of neurons (Figure 5). It is known that slow negative feedback current is responsible for Type 2 PRC [5]. In addition, it is commonly known that most class 2 neurons have Type 2 PRC. These results support the comparable performance between network of class 2 neurons and our model.
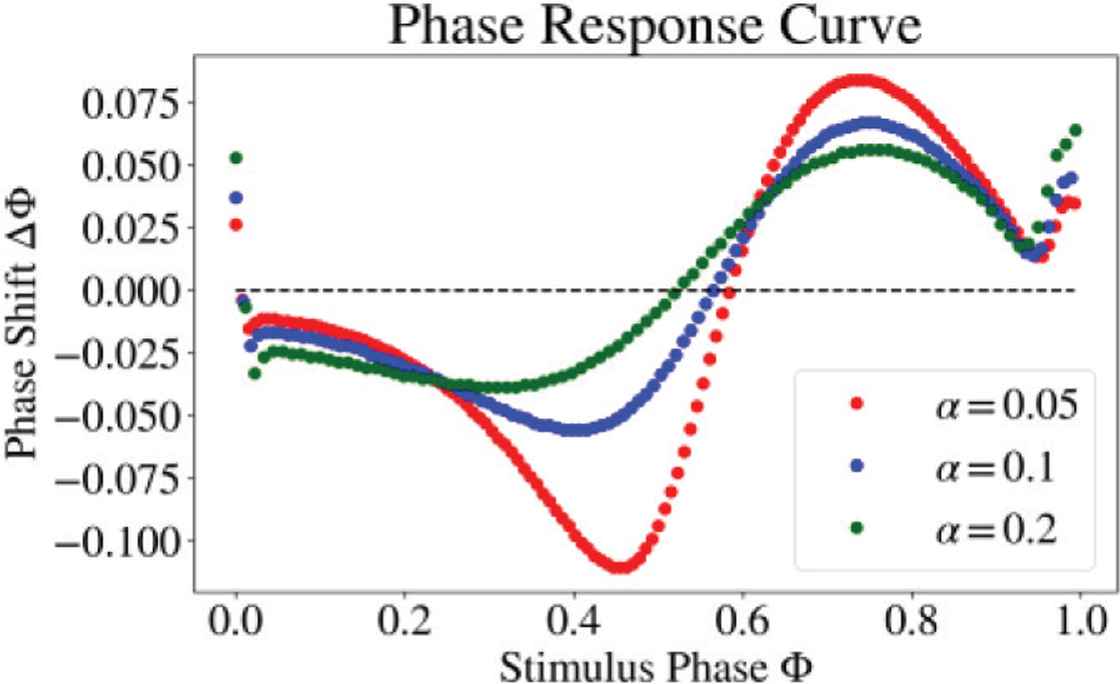
Phase response curve of 3-variable DSSN model.
Phase response curve of Regular Spiking class neuron was computed by applying a perturbation only after the adaptation has fully stabilized to determine a unique firing period. As a result, we found that the zero-phase-shift-crossing point is essentially altered by α which in effect alters the overall retrieval performance. In other words, we may be able to design optimal PRC with α for retrieval tasks.
Magnitude of phase shift (ΔΦ) may not be an essential factor of the performance since increasing the magnitude of neuronal interaction did not give significant improvements (Figure 6).
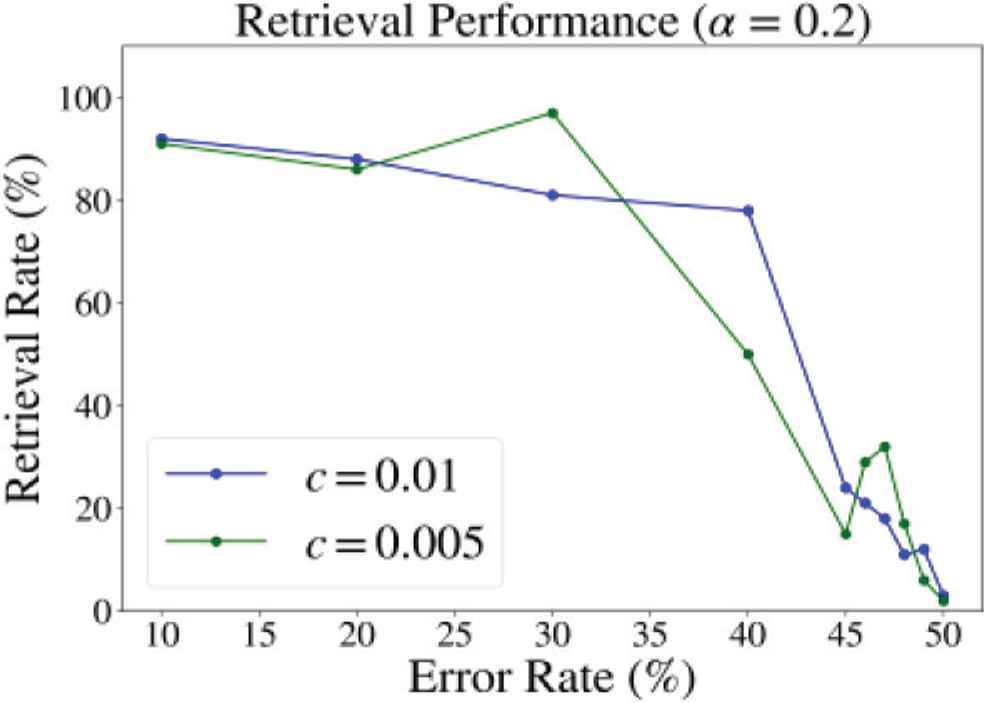
Retrieval performance at c = 0.005 and 0.01 (α = 0.2).
4.2. Moderate Neuronal Interaction
We observed chaotic transition within stored patterns (Chaotic itineracy) when we set moderate neuronal interaction (c = 0.05). Figure 7a shows overlap dynamics with different α. Figure 7b is the staying period distribution without distinguishing patterns which were retrieved for a certain time. Maximum staying period was extended by decreasing α.
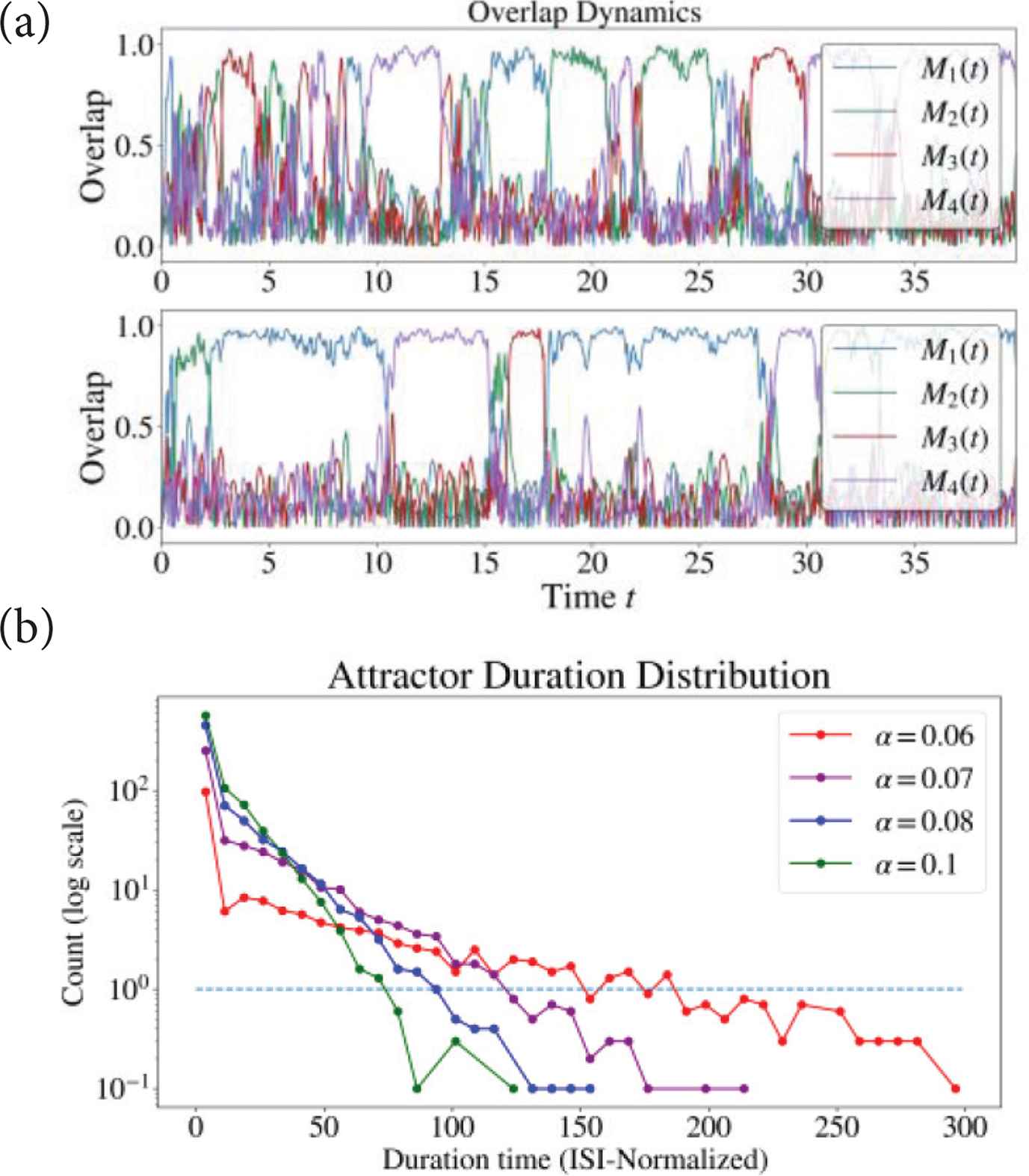
(a) Overlap for c = 0.05. (Top) α = 0.1, (Bottom): α = 0.07. (b) Duration distribution (ISI-Normalized) of the pattern retrieval. Averaged from 10 trials of t = 1000 simulation and 40 bins. Retrieval is defined when overlap exceeded 0.8. Dashed blue line shows when count = 1.0.
Previous study with the discrete Hopfield Network showed that adaptation term has a similar effect as a temperature term which is known to destabilize attractors [6]. Similarly, in our model, variable q and SFA strength α is assumed to be responsible for destabilization of attractors leading to chaotic itineracy.
We then introduced heterogeneity in the network by grading each stored pattern with weight bias wu. “Strong attractors” and “weak attractors” were distinguished by the size of wu. We set w1 = 1.03 and w2,3,4 = 1.0 (Pattern 1 corresponds to the strong attractor and the others weak). Then, we counted how often each pattern was retrieved (when overlap for the pattern exceeded 0.8) and observed the preference of attractor strength being modulated by α (Figure 8). Strong preference for strong attractor is observed at α = 0.1, whereas the preference is relaxed as α is decreased.

Retrieval count of strong attractor and average count of weak attractors. Average computed from 40 trials.
4.3. Transition of Dynamical Behavior
Effects of c and α on the network’s dynamical behavior is analyzed in the following stability matrix (Figure 9). Each value of the matrix is computed by calculating the gradient of the log-scaled Euclidean distance between fiducial trajectories (vector of v, n, q, Is of 256 neurons) and perturbed trajectories. The value approximates largest Lyapunov exponent of 1024 dimension dynamical system. We confirmed that the system is stable at small c region (the gradient of divergence is 0 or below), and becomes chaotic at larger c (positive gradient of divergence). Stability may also be altered by α where smaller value leads to more stable dynamics, although further detailed analysis is needed.
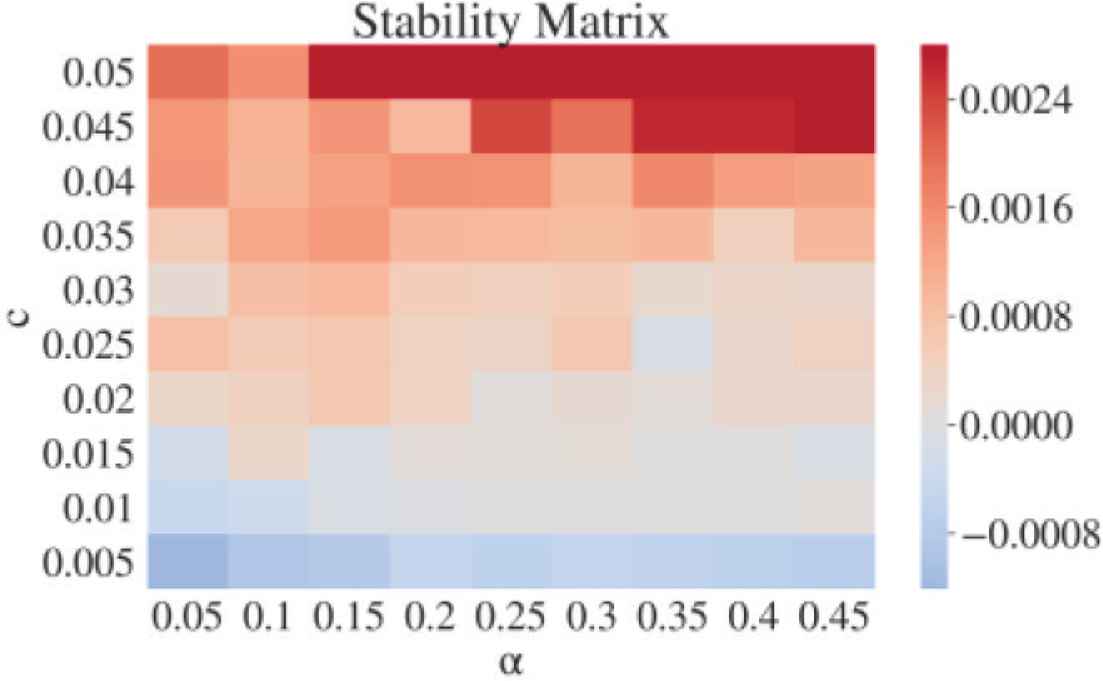
Stability matrix computed from gradient of average divergence (log scale) between fiducial trajectories and 10 perturbed trajectories for each fiducial trajectory. Color bar shows gradient value.
5. DISCUSSION
We constructed an autoassociative memory composed of 3-variable DSSN model which exhibit SFA. As a result, various dynamics were observed at different parameter regions of c and α. By setting small c value, the effect of neuronal interaction may be considered as perturbations applied to each neuron, therefore evoking a characteristic of PRC: Type 2 PRC caused from the slow feedback current led to high retrieval performance. On the other hand, the synchronous network behavior switches to chaotic itineracy when c is increased. In this region, it can be assumed that destabilization effect caused by SFA [6] becomes more significant.
To model the level of Acetylcholine volume, we then investigated α-dependent effects at the above distinct regions resulting in rich dynamics. Although some biological correspondence, especially on the modulation of attractor strength preference (Figure 8) is discussed in the prior research [6], biological plausibility of our numerical simulation results such as duration distribution of the retrieval (Figure 7) need to be discussed in future.
From the engineering perspective, it is known that all-to-all connected networks are applicable to solving optimization problems [10]. Moreover, chaotic dynamics can be utilized to escape the local minima and obtain the global minima [11]. Similarly, our spiking neural network may be developed to solve optimization problems on low power hardware in the future. All results in this work were obtained by floating-point operations on software simulation (Euler method dt = 0.000375). One of the future works is to implement our models in fixed-point operations on FPGA devices.
APPENDIX
| Par. | Val. | Par. | Val. | Par. | Val. |
|---|---|---|---|---|---|
| afn | 8.0 | bfn | −0.25 | cfn | −0.5 |
| afp | −8.0 | bfp | 0.25 | cfp | 0.5 |
| agn | 4.0 | bgn | −2−4 - 2−5 | cgn | −0.77083333 |
| agp | 16.0 | bgp | 2−5 - 2−2 | cgp | −0.6875 |
| τ | 2−9 | ϕ | 0.625 | rg | −0.26041666 |
| ɛ | 0.03 | v0 | −0.41 | I0 | −0.09 |
Par., Parameter; Val., Value. (v0 and ɛ take original values in this paper.)
Parameter set for 3-variable DSSN model
CONFLICTS OF INTEREST
The authors declare they have no conflicts of interest.
ACKNOWLEDGMENTS
This work was supported by
AUTHORS INTRODUCTION
Mr. Naruaki Takano
 He is a graduate student at the University of Tokyo, Graduate School of Information Science and Technology. He received his B.S. in Information Science from Tokyo Institute of Technology in 2018. His research interests include computational neuroscience and network modeling.
He is a graduate student at the University of Tokyo, Graduate School of Information Science and Technology. He received his B.S. in Information Science from Tokyo Institute of Technology in 2018. His research interests include computational neuroscience and network modeling.
Dr. Takashi Kohno
 He has been with the Institute of Industrial Science at the University of Tokyo, Japan since 2006, where he is currently a Professor. He received the BE degree in medicine in 1996 and the PhD degree in mathematical engineering in 2002 from the University of Tokyo, Japan.
He has been with the Institute of Industrial Science at the University of Tokyo, Japan since 2006, where he is currently a Professor. He received the BE degree in medicine in 1996 and the PhD degree in mathematical engineering in 2002 from the University of Tokyo, Japan.
REFERENCES
Cite this article
TY - JOUR AU - Naruaki Takano AU - Takashi Kohno PY - 2020 DA - 2020/05/18 TI - Neuromorphic Computing in Autoassociative Memory with a Regular Spiking Neuron Model JO - Journal of Robotics, Networking and Artificial Life SP - 63 EP - 67 VL - 7 IS - 1 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.200512.013 DO - 10.2991/jrnal.k.200512.013 ID - Takano2020 ER -
