1. INTRODUCTION

Over the past few decades, distributed coordination control of Multi-Agent Systems (MASs) is a research focus and attracts lots of attentions from many fields. Among them, consensus problem is a fundamental problem, aiming at this problem, numerous of good results have been reported. A theoretical framework for analysis of consensus for MASs was built in Olfati-Saber et al. [1], and had great influence. Besides, others of excellent results have been reported, such as asynchronous consensus [2], leader following consensus [3], finite-time consensus [4] and so on [5,6].

It is common to find that there always exist lots of collective motions in nature and reality engineering, such as the distributed formation flight of satellites around the moon while the moon moving around the earth, flocks of birds flying around a closed circle and so on. Recently, to imitate or explain such kinds of motions, the collective rotating motions of second-order MASs was investigated in Lin and Jia [7], based on which, Lin et al. [8], made a further study on the distributed composite-rotating consensus of second-order MASs. Furthermore, rotating consensus [9], common finite-time rotating encirclement control [10], and the influence of non-uniform delays on distributed rotating consensus [11] was investigated. Moreover, notice the fact that, groups of agents may require to maintain desired formation during this process, therefore, the formation control of MASs was investigated, such as Xiao et al. [12], Xue et al. [13], and Meng et al. [14].

Notice that the above-mentioned works all assumed that the information exchange between different agents is ideal, that is, each agent can obtain its neighbor’s information accurately. However, in reality, the communications among different agents may be interfered by stochastic communication noise, which may lead to great negative influence on the stability of the system. It is meaningful to design proper control protocol such that the stochastic communication noises can be countered. The consensus control problem of MASs with communication noises were solved in Li and Zhang [15], Cheng et al. [16], Guo et al. [17], and Sun et al. [18]. The mean-square composite-rotating consensus problem of second-order MASs with communication noises was addressed by introducing a time-varying consensus gain in the control protocol [19]. Since the formation is considered and a time-varying consensus gain is introduced into the control protocol to attenuate the stochastic communication noises, though the origin closed-loop system is changed into an equivalent closed-loop system by taking a coordinate transformation, it is still difficult to obtain the eigenvector of the matrix. Therefore, the methods proposed in Li and Zhang [15], Cheng et al. [16], Guo et al. [17], Sun et al. [18], and Mo et al. [19] cannot be directly extended to achieve the quasi-­composite rotating formation control of MASs under stochastic communication noises. Up-to-date, it is a pity to find that there is no result on composite-rotating formation control of MASs with stochastic communication noises.

Motivated by the above discussions, the mean-square quasi-composite rotating formation control of second-order MASs with stochastic communication noises is considered in this paper as a response to the lack of corresponding researches, by using which the actual physical system can be described more precisely. The main contributions of this paper can be summarized as follows: (i) In contrast with Mo et al. [20], where the quasi-composite rotating formation control of MASs was solved without communication noises, the results of this paper are more realistic. (ii) The definition of the mean square quasi-composite rotating formation of MASs is first proposed. (iii) A novel distributed control protocol with a time-varying control gain is designed, by using which the stochastic communication noises can be attenuated. (iv) By using the theory of stochastic differential equation and proper coordination transformation, it is proved that under some mild conditions, the desired formation can be achieved.

The rest of this paper is organized as follows. In Section 2, the theories of algebraic graph are introduced. Section 3 describes the system models and the problem under investigation. In Section 4, the definition of mean-square quasi-composite rotating formation is given, besides a novel distributed control protocol and sufficient conditions are deduced for achieving mean-square quasi-composite rotating formation of MASs. A numerical simulation is given in Section 5 to verify the effectiveness of theoretical results we proposed. Finally, a conclusion is made for this paper in Section 6. Notations: Throughout this paper, let ℝ and ℂ denote the sets of real numbers and complex numbers; Let I_n ∈ ℝ^n×n (O_n ∈ ℝ^n×n) be the n × n identity (zero) matrix, 1_n ∈ ℝⁿ denote the n × 1 column vector of all ones; Let diag{s₁, s₂, ..., s_n} ∈ ℝ^n×n denotes the diagonal matrix with diagonal entries s₁, s₂, ..., s_n; j represents the imaginary unit; A^* represents the conjugate transpose of matrix A; For complex vector x ∈ ℂⁿ, ||x||² = x^*x; tr(P) represents the trace of P; (·)^T denotes the transpose of a real matrix; (·)⁻¹ denotes the inverse of a invertible matrix; λ_max(·) denotes the maximum eigenvalue of a real symmetric matrix.

2. PRELIMINARIES

Theories of algebraic graph [21]. Let (𝒱, ε, 𝒜) be an undirected graph with n nodes, 𝒱 = {1, 2, ..., n} represents the set of nodes, and ε ⊆ 𝒱 × 𝒱 represents the set of edges, 𝒜 = [a_ij] represent the weighted adjacency matrix. Let N_i = {j ∈ 𝒱: (j, i) ∈ ε} denotes the neighbors set of node i, ℒ = [l_ij] denotes the Laplacian of graph 𝒢. Graph 𝒢 is said to be connected if there exists a path between every two distinct nodes.

3. MODEL AND PROBLEM STATEMENT

Consider a multi-agent system with n agents, the dynamics of each agent are given as follows [Equations (1) and (2)]:

where i = 1, 2, ..., n, r_i(t) ∈ ℂ, ṽ_i(t) ∈ ℂ, u_i(t) ∈ ℂ respectively denotes the position, velocity and control input of the ith agent.

In this paper, our objective is to design a distributed control protocol by local information to assure that the effect of stochastic communication noises can be counteracted, and all agents surround a moving point with a desired structure and a constant angular velocity ω₁ > 0 while the moving point surrounds the origin with a constant angular velocity ω₂ > 0.

4. MAIN RESULTS

In this section, the mean-square quasi-composite rotating formation control of MASs (1) and (2) is investigated.

Let vi(t)=ω1ω1+ω2(v˜i(t)+jω2ri(t)), ci(t)=ri(t)+jω 1−1vi(t), i = 1, 2, ..., n denotes the relative velocity and the center of the rotation of the ith agent respectively.

Suppose that the information exchange among the agents is affected by the stochastic communication noises. The information of the ith agent received from its neighbor agents is defined as follows:

where k ∈ N_i, {η_rik, η_ṽik}, i, k = 1, 2, ..., n are independent standard white noises, {σ_rik, σ_ṽik} are the finite noise intensities.

The definition of the mean-square quasi-composite rotating formation is given as follows:

In this paper, the following distributed control protocol is proposed:

where a(t) > 0 is a time-varying consensus control gain.

To continue, we need the following assumptions.

From vi(t)=ω1ω1+ω2(v˜i(t)+jω2ri(t)) and ci(t)=ri(t)+jω 1−1vi(t), we have [Equation (9)]

Furthermore, together (1) we have [Equation (10)]

Then, we have

which implicates that

Furthermore, we have

Let δ(t) = (v₁(t), c₁(t), ..., v_n(t), c_n(t))^T, then the closed-loop system (9) and (10) can be rewritten as where A=(jω100−jω2), B1=(−10−jω 1−10), B2=(0−10−jω 1−1), ℒ˜=F−1HℒH*F−1, F = diag{ρ₁, ..., ρ_n}, H = diag{e^jθ₁, ..., e^jθ_n}, η=(η 1T,⋯,η nT)T∈ℂ2n2, where η_i = (σ_ri1, σ_ṽi1, ..., σ_rin, σ_ṽin)^T ∈ ℂ²ⁿ, Ω = diag{Ω₁, ..., Ω_n} ∈ ℂ^2n×2n2, Ωi=ω1ω1+ω2(ai1(ρ1+jω2ρiej(θi−θ1)ρ1jω 1−1ρ1+ρiej(θi−θ1)ρ1jρ1−ω2ρiej(θi−θ1)ω1ρ1−ω 1−1ρ1+jρiej(θi−θ1)ω1ρ1),…,ain(ρn+jω2ρiej(θi−θn)ρnjω 1−1ρn+ρiej(θi−θn)ρnjρn−ω2ρiej(θi−θn)ω1ρn−ω 1−1ρn+jρiej(θi−θn)ω1ρn)), i = 1, 2, ..., n.

Next, let us prove that other eigenvalues of Φ have negative real part. Let λ₀ ≠ 0 be an arbitrary eigenvalue of Φ and [ x 1Tx 2T ]T∈ℂ2n is its eigenvector associated to λ₀. Thus

which leads to λ₀x₁ = jω₁ λ₀x₂ and x2=−jω 1−1x1. Together with (18), we have −ℒ˜x1+jω 1−1ℒx1=λ0x1, i.e.,

Consider the following auxiliary system:

Take 𝒱(t) = x^*(t) x(t), along system (21), we have

Therefore, Re(λ₀) ≤ 0. If λ₀ = jb, b ≠ 0 and V˙(t)=0. By Lasalle’s invariant theorem, we have x₁ ∈ span{FH1_n}, thus ℒx1=−jω 1−1λ0x1, i.e., ℒFH1n=−jω 1−1λ0FH1n. Noted that zero is an eigenvalue of ℒ, we have 1 nTx1=0, i.e., 1 nTFH1n=∑k=1nρkejθk=0, which is contradicted with Assumption 2. Therefore, we have Re(λ₀) < 0.

Then, the origin system can be decoupled into the following system:

In view of the theory of stochastic differential equation, the solution of (29)–(31) is

where W(t) = (W_r11(t), W_ṽ11(t),...,W_r1n(t), W_ṽ1n(t),...,W_rn1(t), W_ṽn1(t), ..., W_rnn(t), W_ṽnn(t))^T and W_rik(t), W_ṽik(t), i, k = 1, 2, ..., n are standard Brownian motions. Therefore, we have

Since all eigenvalues of Λ have negative real parts, this together Lemma 3 with Assumptions 3, we have limt→+∞E[ ‖ ζ¯(0) ‖2e2Real(λmax(Λ))∫0ta(τ)dτ ]=0. Furthermore, together with Assumption 4, we have limt→+∞E[(2n−2)∫0ta2(τ)e2Real(λmax(Λ))∫τta(s)dsdτ=0. Therefore, we have

Together δ(t) = Uζ(t) with (32) and (33), we have

Let v(t) = (v₁(t), v₂(t),...,v_n(t))^T, c(t) = (c₁(t), c₂(t),...,c_n(t))^T, we can obtain that limt→+∞E||v(t)−FH1nejω1tζ1(0)−FH1n∫0tejω1tγ1a(τ)ΩdW(τ)||2=0, and limt→+∞E||c(t)−1ne−jω2tζ2(0)−1n∫0te−jω2tγ2a(τ)ΩdW(τ)||2=0.

Since limt→+∞E||FH1n∫0tejω1tγ1a(τ)ΩdW(τ)||2=0, and limt→+∞E||1n∫0te−jω2tγ2a(τ)ΩdW(τ)||2=0, then we have

which indicates that conditions (4)–(7) are satisfied, i.e., the desired formation control of MASs (1) and (2) is achieved.

5. A NUMERICAL EXAMPLE

To demonstrate the effectiveness of the proposed theoretical results, consider MASs with six nodes. The communication topology graph of the MASs is shown in Figure 1, from which we could see that the communication topology graph is connected such that the Assumption 1 is satisfied. Without loss of generality, we assume that the weight of each edge is 1. Then consider the MASs (1) and (2), where the control input in (2) is chosen as the distributed control protocol (8). The initial conditions of the system are taken as r₁(0) = −2.8 – 4.8j, r₂(0) = 1.7 + 4.2j, r₃(0) = −1.1 + 6.2j, r₄(0) = 3 + 5j, r₅(0) = −1 + 6j, r₆(0) = 3 + 5.3j, ṽ₁(0) = 2.1, ṽ₂(0) = 2.8, ṽ₃(0) = −0.9, ṽ₄(0) = −2, ṽ₅(0) = −1, ṽ₆(0) = −2.2. Take a(t)=21+t, ω₁ = 0.8, ω₂ = 0.02, θi=πi6, i = 1, 2, ..., 6 and choose ρ₁ = 2, ρ₂ = 0.5, ρ₃ = 1.5, ρ₄ = 2.5, ρ₅ = 1, ρ₆ = 2.5.

Figure 1

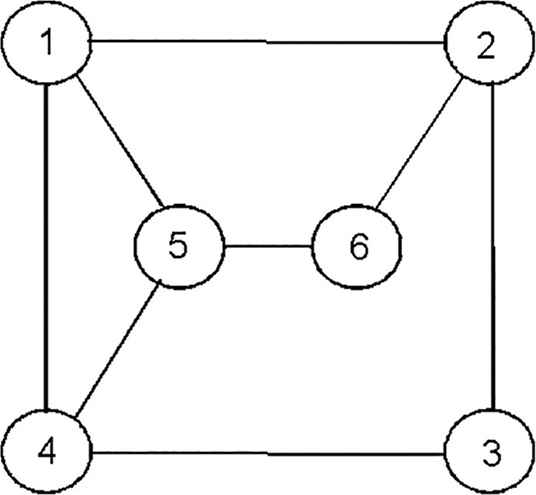
The communication topology graph.

Figure 2 shows the position trajectories of the MASs, from which we could see that all agents finally surround a common moving point with a desired formation. Figure 3 shows the trajectories of the moving rotating centers, from which we could see that the moving points finally surround the origin with a constant angular velocity. We could see the whole (Figure 4) and local (Figure 5) trajectories of the position and moving rotating centers of the MASs for more intuitive, which implicates that Theorem 1 is effective. Besides, it is clear from Figures 6 and 7 that the control input value of each agent tends to a bounded value as time tends to infinity.

Figure 2

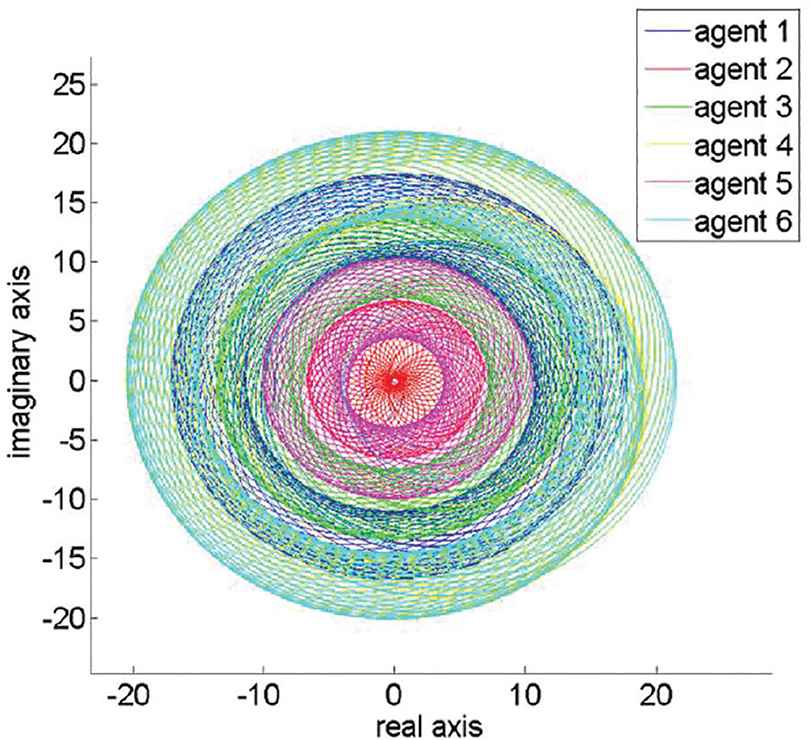
Position trajectories of the MASs.

Figure 3

Trajectories of the moving rotating centers.

Figure 4

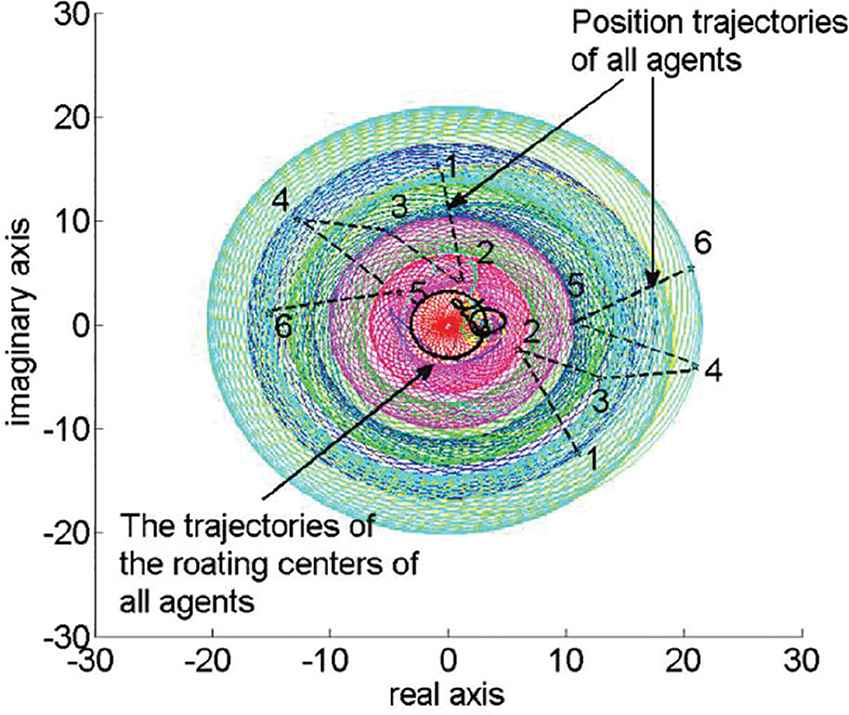
Whole trajectories of the position and moving rotating centers of the MASs.

Figure 5

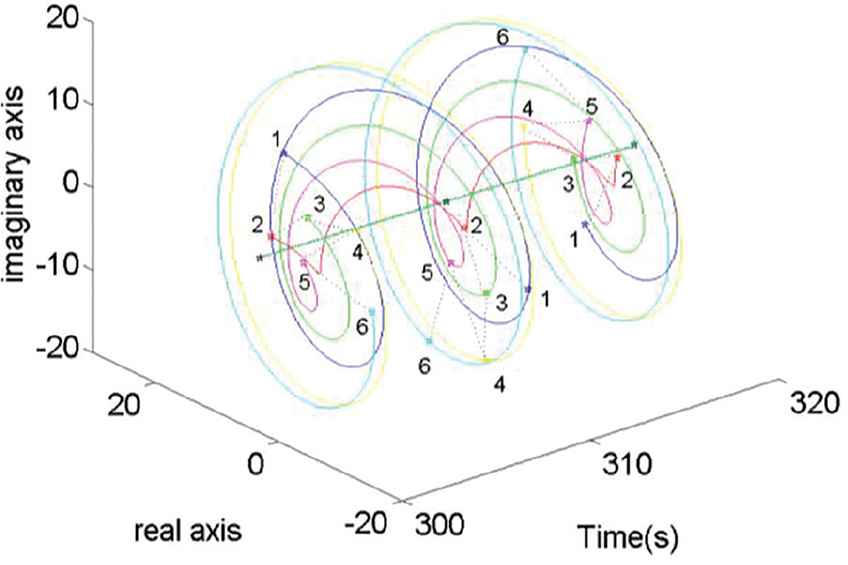
Local trajectories of the position and moving rotating centers of the MASs.

Figure 6

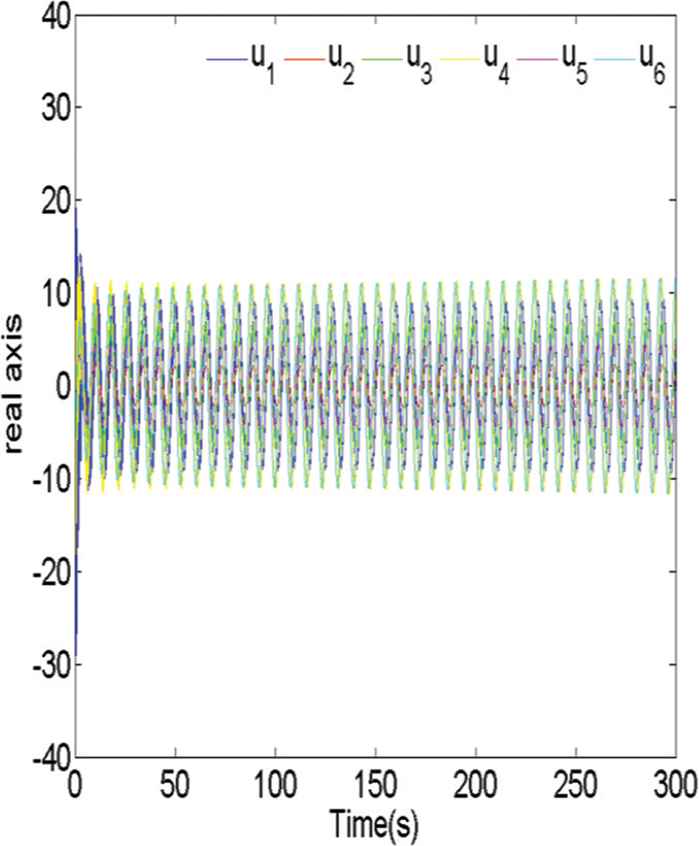
Trajectories of the control inputs of the MASs (the real part).

Figure 7

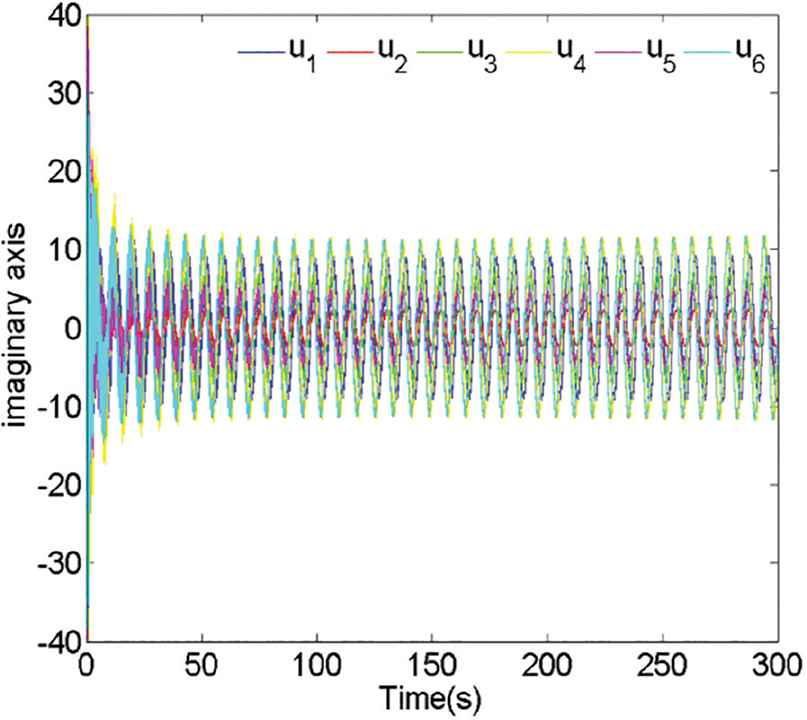
Trajectories of the control inputs of the MASs (the imaginary part).

6. CONCLUSION

The mean-square quasi-composite rotating formation problem of second-order MASs with stochastic communication noises was investigated in this paper. A novel distributed control protocol with a time-varying control gain was designed. And then, corresponding sufficient conditions were deduced. Besides, the effectiveness of the proposed theoretical results was confirmed via a numerical example.

ACKNOWLEDGMENTS

This work was supported by the Beijing Educational Committee Foundation [No. KM201910011007 and No. PXM2019_014213_000007], the Beijing Natural Science Foundation [No. Z180005] and the Graduate Research Capacity Improvement Program of 2019.

Authors Introduction

Prof. Lipo Mo

He received his B.S. degree in Department of Mathematics, Shihezi University, China, in 2003, and the PhD degree in School of Mathematics and Systems Science from the Beihang University, Beijing, in 2010. Currently, he is an Associate Professor at Beijing Technology and Business University. His research interests include stochastic systems, coordination control of multi-agent systems, and distributed optimization.

Mrs. Xiaolin Yuan

She received her B.S. degree in School of Science, Beijing Technology and Business University, China, in 2017. Currently, she is pursuing the Master degree in control theory in School of Mathematics and Statistics, Beijing Technology and Business University. Her research interests include coordination control of Fractional order multi-agent systems.

Prof. Yingmin Jia

He received his B.S. degree in Control Theory from Shandong University in 1982, and his M.S. and PhD degrees both in Control Theory and Applications from Beihang University (BUAA), Beijing, China, in 1990 and 1993, respectively. In 1993, he joined the Seventh Research Division at Beihang University, where he is currently a Professor of automatic control. His current research interests include robust control, adaptive control and intelligent control, and their applications in industrial processes and vehicle systems.

Dr. Shaoyan Guo

He received his B.S. and M.S. degree in school of Science, Beijing Technology and Business University, China, in 2015 and 2018. Currently, he is a PhD candidate in control science and engineering in Shien-Ming Wu School of Intelligent Engineering, South China University of Technology. His research interests include coordination control of multi-agent systems