Journal of Nonlinear Mathematical Physics

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 26, Issue 1, December 2018, Pages 107 - 132

Rational solutions to Q3δ in the Adler-Bobenko-Suris list and degenerations

Authors
Song-lin Zhao*
Department of Applied Mathematics, Zhejiang University of Technology Hangzhou, 310023, Zhejiang, P.R. China,songlinzhao@zjut.edu.cn
Da-jun Zhang*
Department of Mathematics, Shanghai University Shanghai, 200444, P.R. China,djzhang@staff.shu.edu.cn
*Corresponding author
Corresponding Authors
Song-lin Zhao, Da-jun Zhang
Received 15 October 2017, Accepted 25 August 2018, Available Online 6 January 2021.
DOI
10.1080/14029251.2019.1544793How to use a DOI?
Keywords
NQC equation; ABS list; Casoratian; rational solutions
Abstract

We derive rational solutions in Casoratian form for the Nijhoff-Quispel-Capel (NQC) equation by using the lattice potential Korteweg-de Vries (lpKdV) equation and two Miura transformations between the lpKdV and the lattice potential modified KdV (lpmKdV) and the NQC equation. This allows us to present rational solutions for the whole Adler-Bobenko-Suris (ABS) list except Q4. The known Miura transformation for soliton solutions between the NQC equation and Q3δ and the known degenerations for solitons from Q3δ to Q2, Q1δ, H3δ, H2 and H1 in the ABS list are used. We show that the Miura transformation and degenerations are valid as well for rational solutions which are usually considered as “long-wave-limit” of solitons. All the rational solutions can be expressed in terms of {zj} which are linear functions of (n, m).

Copyright
© 2019 The Authors. Published by Atlantis and Taylor & Francis
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

1. Introduction

In recent years multidimensional consistency [22] has become increasingly popular as one of interpretations of integrability for lattice equations. With this property and two mild additional requirements on lattice equations: symmetry and the so-called ‘tetrahedron property’, Adler, Bobenko and Suris (ABS) classified integrable affine linear models defined on an elementary quadrilateral [3]. Their results are known as the ABS list, which consists of nine lattice equations: Q4, Q3δ, Q2, Q1δ, A2, A1δ, H3δ, H2, H1. Some of these equations have been known before, for example, H1 is the lattice potential Korteweg-de Vries (lpKdV) equation [21], H3δ=0 is the lattice potential modified KdV (lpmKdV) equation [21], Q1δ=0 is the lattice Schwarzian KdV (lSKdV) equation [20] and Q4 is known as the Adler’s equation [2] which is the nonlinear superposition formula of the Krichever-Novikov equation. After introducing some new parameters [19], the lattice equations given originally by ABS [3] can be written as

Q3δ:P(uu^+u˜u˜^)−Q(uu˜−u^u˜^)=(p2−q2)((u˜u^+uu˜^)+δ24PQ),(1.1a)
Q2:(q2−a2)(u−u^)(u˜−u˜^)−(p2−a2)(u−u˜)(u^−u˜^)+(p2−a2)(q2−a2)(q2−p2)(u+u˜+u^+u˜^)=(p2−a2)(q2−a2)(q2−p2)((p2−a2)2+(q2−a2)2−(p2−a2)(q2−a2)),(1.1b)
Q1δ:(q2−a2)(u−u^)(u˜−u˜^)−(p2−a2)(u−u˜)(u^−u˜^)=δ2a4(p2−q2)(p2−a2)(q2−a2),(1.1c)
H3δ:P(a2−q2)(uu˜+u^u˜^)−Q(a2−p2)(uu^+u˜u˜^)=δ(p2−q2),(1.1d)
H2:(u−u˜^)(u˜−u^)+(p2−q2)(u+u˜+u^+u˜^)=p4−q4,(1.1e)
H1:(u−u˜^)(u^−u˜)=p2−q2,(1.1f)
where in (1.1a) (p, P) = 𝔭 and (q, Q) = 𝔮 are the points on the elliptic curve
{(x,X)|X2=(x2−a2)(x2−b2)},(1.2)
and in (1.1d)
P2=a2−p2,   Q2=a2−q2.(1.3)

Q4 will be considered elsewhere, which is not listed here. We omit A1δ and A2 from the above list because of the equivalence between A1δ and Q1δ by u → (−1)n+mu, and between A2 and Q3δ=0 by u → u(−1)n+m. In Eqs. (1.1), δ is a constant; u = un,m := u(n, m) denotes dependent variable of lattice points labeled by (n, m) ∈ 𝕑 2; p and q are continuous lattice parameters associated with the grid size in the directions of the lattice given by the independent variables n and m, respectively; notations with elementary lattice shifts are denoted by

u=un,m,   u˜=un+1,m,   u^=un,m+1,   u˜^=un+1,m+1.

There are many ways of degenerations among the lattice equations in the list (1.1) [3, 4, 19].

Various approaches have been shown to be significant in deriving soliton solutions for the ABS list as evidenced by a series of papers. Atkinson, Hietarinta and Nijhoff constructed N-soliton solutions to Q3δ in terms of the τ-function of the Hirota-Miwa equation. The corresponding solutions were expressed by the usual Hirota’s polynomial of exponentials [5]. By developing Hirota’s direct method, Hietarinta and Zhang derived N-soliton solutions to H-series of equations and Q1δ [14]. Their method is algorithmic and based on multidimensional consistency, progressing in each case from background solution to 1-soliton solution and to N-soliton solutions, where many Casoratian shift formulae were established. Meanwhile, Nijhoff and collaborators proposed Cauchy matrix approach [19] to catch the N-soliton solutions for lattice equations in the ABS list except Q4. The authors of the present paper extended Cauchy matrix approach to a generalised case [30], which can be used to construct more kinds of exact solutions beyond soliton solutions for integrable systems (see also Ref. [25]), e.g., multiple-pole solutions. Inverse Scattering Transform was also established to solve some ABS equations [8, 9]. As the ‘master’ and the most complicate equation in this list, Q4 was solved by using Bäcklund transformation [6, 7].

Different from soliton solutions, rational solutions are usually expressed by fraction of polynomials of independent variables. Generally speaking, such type of solutions can be derived from soliton solutions through a special limit procedure (see Refs. [1, 26, 31] as examples). Compared with the case in continuous integrable systems, it is more difficult to get rational solutions of lattice equations. In spite of this, until now much progress has been got. Algebraic solutions and lump-like solutions for the Hirota-Miwa equation were, respectively, given in Refs. [17] and [12]. With the help of bilinear method [14], rational solutions for H3δ and Q1δ as well as the lattice Boussinesq equation were obtained in recent papers [23, 24]. Besides, by imposing reduction conditions on rational solutions of the Hirota-Miwa equation, rational solutions for the lpKdV equation and two semi-discrete lpKdV equations were obtained [10].

Recently, in [28] a transformation approach was employed to construct rational solutions for the ABS list (1.1) except Q3δ. Those transformations used in [28] are nonauto-Bäcklund transformations (Miura-type transformation) in which spectral parameters are absent. This is just the case of rational solutions that requires spectral parameters varnished. More examples can be found in [28]. However, the transformation connected to Q3δ is too complicated to be used for generating rational solutions.

If we forget about Q4, then Q3δ can act as a top equation in the ABS list in the sense that other “lower” equations can be obtained as degenerations of Q3δ [19]. Note that solutions in terms of Cauchy matrix given in [19, 30] are not available to generate rational solutions by taking “long-wave-limit” as done in Casoratian form (cf. [23]).

In this paper we aim to construct rational solutions to Q3δ. It is known that the Nijhoff-Quispel-Capel (NQC) equation (cf. [21]) is in some sense Q30 and by transformation solutions of Q3δ can be expressed in terms of solutions of the NQC equation [19]. Our strategy is the following. First we construct Casoratian solutions for the NQC equation so that rational solutions can be included. Then we examine the degeneration procedure given in [19] and present rational solutions for Q3δ and “lower equations” in the ABS list.

The paper is organised as follows. In Sec. 2, we explain our plan of solving the NQC equation and describe relations between the NQC equation and Q3δ. In Sec. 3, we solve the NQC equation by means of bilinear method and derive its rational solutions in Casoratian form. In Sec. 4, degenerations of Q3δ are analyzed and rational solutions for “lower equations” Q2, Q1δ, H3δ, H2 and H1 in (1.1) are obtained. Sec. 5 is for conclusions. In addition, two appendices are given as complements to the paper.

2. NQC and Q3δ

2.1. Plan of solving the NQC equation

The celebrated NQC equation [21] takes the form

1+(p−a)S(a,b)−(p+b)S˜(a,b)1+(q−a)S(a,b)−(q+b)S^(a,b)=1−(q+a)S˜^(a,b)+(q−b)S˜(a,b)1−(p+a)S˜^(a,b)+(p−b)S^(a,b),(2.1)
where S(a, b) = S(b, a) are functions of (n, m) with (a, b) being branch point parameters, p and q are spacing parameters of n and m, respectively.

The known solutions of the NQC equation are obtained by means of Cauchy matrix [19, 30], which do not allow to take “long-wave-limit”. To derive Casoratian solutions of this equation, we introduce the following system

1+(p−a)S(a,b)−(p+b)S˜(a,b)=V˜(a)V(b),(2.2a)
1+(q−a)S(a,b)−(q+b)S^(a,b)=V^(a)V(b),(2.2b)
p−q+w^−w˜=1V˜^(a)((p−a)V^(a)−(q−a)V˜(a))(2.2c)
=1V(a)((p+a)V˜(a)−(q+a)V^(a)),(2.2d)
p+q+w−w˜^=1V˜(a)((p−a)V(a)+(q−a)V˜^(a))(2.2e)
=1V^(a)((p+a)V˜^(a)+(q−a)V(a)),(2.2f)
(p−q+w^−w˜)(p+q+w−w˜^)=p2−q2,(2.2g)
together with assuming symmetric property
S(a,b)=S(b,a),(2.3)
where V(a) is a function of (n, m) with a as a parameter, V(b) = V(a)|a→b, w is a function of (n, m) but independent of (a, b). Before we proceed, let us give some remarks on the above system. Firstly, this system is consistent and solvable. In fact, all the equations in (2.2) appeared in a same Cauchy matrix scheme (e.g. Eqs. (9.47, 9.53, 9.54) in [13] or (2.21, 2.37, 2.41) in [19]), which means they have solutions in terms of Cauchy matrix. Secondly, (2.2) contains Miura (nonauto-Bäcklund) transformations of several integrable equations. In fact, (2.2g) is known as the lpKdV equation [20]; the right hand sides of (2.2c,2.2d) yield a parameter-extended lpmKdV equation
V(a)[(p−a)V^(a)−(q−a)V˜(a)]=V˜^(a)[(p+a)V˜(a)−(q+a)V^(a)],(2.4)
which comes from the right hand sides of (2.2e,2.2f) as well as from eliminating w from (2.2c)–(2.2f); with assumption (2.3), eliminating V from (2.2a, 2.2b) one gets the NQC equation (2.1). Thus, (2.2a)–(2.2f) are understood as Miura transformations connecting the lpKdV (2.2g), extended lpmKdV (2.4) and NQC equation (2.1). Finally, we can conclude that under assumption (2.3) once the system (2.2) is solved, so is the NQC (2.1).

2.2. From NQC to Q3δ

In Ref. [19], soliton solutions for Q3δ (1.1a) were written as a linear combination of four terms each of which contains as an essential ingredient the soliton solution of the NQC equation (2.1). Since solutions of the NQC equation can be provided by system (2.2) with assumption (2.3), in the following we describe relations between Q3δ and the system (2.2) together with (2.3).

Theorem 2.1.

The solution of Q3δ (1.1a) is formulated by

u=AϜ(a,b)[1−(a+b)S(a,b)]+BϜ(a,−b)[1−(a−b)S(a,−b)]+CϜ(−a,b)[1+(a−b)S(−a,b)]+DϜ(−a,−b)[1+(a+b)S(−a,−b)],(2.5)
in which S(a, b) satisfies the system (2.2) and symmetry (2.3), function Ϝ(a, b) is defined as
Ϝ(a,b)=(P(p−a)(p−b))n(Q(q−a)(q−b))m,(2.6)
and P, Q are defined by (1.2); A, B, C and D are constants subject to the constraint
AD(a+b)2−BC(a−b)2=−δ216ab.(2.7)

The proof is similar to the one given in [19]. We skip it here and leave it in Appendix A.

According to this Theorem, any solution S(a, b) solved from the system (2.2) with (2.3), including rational solutions, will generates a solution to Q3δ via formula (2.5).

3. Rational solutions to the NQC equation (2.1)

In this section, we construct rational solutions for the NQC equation (2.1) by solving system (2.2). Bilinear method will be employed and solutions will be presented in terms of Casoratians. Some Casoratian techniques developed in the literatures [14, 16] will be adopted.

3.1. Preliminary

Casoratian can be viewed as a discrete version of Wronskian. Let us consider functions ϕj with 5 independent variables n, m, α, β, l ∈ 𝕑:

φj(l)=ρj+(p+kj)n(q+kj)m(a+kj)α(b+kj)β(c+kj)l   +ρj−(p−kj)n(q−kj)m(a−kj)α(b−kj)β(c−kj)l,(3.1)
where ρj±, kj, p, q, a, b, c ∈ ℂ and we denote it by ϕj(l) without confusion. Let
φ(l)=(φ1(l),φ2(l),…,φN(l))T.(3.2)

Define a N × N Casoratian

f=|φ(0),φ(1),φ(2),…,φ(N−1)|=|0,1,2,…,N−1|=|N−1^|,(3.3)
where M^ is a compact form standing for consequtive columns (0, 1, 2,...,M) (cf. [11]). With this notation it is easy to understand |N−2^,N|=|0,1,…,N−2,N|, etc. In addition to the above notations, we need the following Laplace expansion identity for Casoratian verification [11].

Lemma 3.1.

Suppose that G is a N × (N − 2) matrix, and a,b,c,d are Nth-order column vectors, then

|G,a,b||G,c,d|−|G,a,c||G,b,d|+|G,a,d||G,b,c|=0.(3.4)

Note that ϕj(l) defined in (3.1) can be regarded as a 5-dimensional function isotropically defined on 5 directions (n, m, α, β, l) together their spacing parameters (p, q, a, b, c). For convenience, we label these 5 directions by

n1=n,   n2=m,   n3=α,   n4=β,   n5=l,(3.5a)
together with their spacing parameters by
p1=p,   p2=q,   p3=a,   p4=b,   p5=c.(3.5b)

We also introduce shift operators T±ni,

T±nif=f(ni±1).(3.5c)

It is then easy to find shift relations for ϕ(l)a

(pi−pj)φ(l)=(Tni−Tnj)φ(l),   i,j∈{1,2,3,4,5},i<j.(3.6)

Besides ϕj(l) in (3.1), we also introduce auxiliary functions and vecors

ϕj(l)=(p2−kj2)−nφk(l),   φ(l)=(ϕ1(l),ϕ2(l),…,ϕN(l))T,(3.7a)
ψj(l)=(q2−kj2)−mφj(l),   ψ(l)=(ψ1(l),ψ2(l),…,ψN(l))T,(3.7b)
ϖj(l)=(a2−kj2)−αφj(l),    ϖ(l)=(ϖ1(l),ϖ2(l),…,ϖN(l))T,(3.7c)
χj(l)=(b2−kj2)−βφj(l),   χ(l)=(χ1(l),χ2(l),…,χN(l))T.(3.7d)

These vectors are necessary in Casoratian verifications (cf. [14]). They obey shift relations slightly different from each other. Suppose σ(l) is one of the above vectors and ε = (ε1, ε2, ε3, ε4). Then shift relations of σ(l), including (3.6), can be expressed through a universal formula

(pi−εipj)σ(l)=(Tεini−εiTnj)σ(l),   i,j∈{1,2,3,4,5},i<j,(3.8a)
where ε varies with σ(l):
σ(l)=φ(l),   ε=(1,1,1,1),(3.8b)
σ(l)=σ[n1](l)≐φ(l),   ε=(−1,1,1,1),(3.8c)
σ(l)=σ[n2](l)≐ψ(l),   ε=(1,−1,1,1),(3.8d)
σ(l)=σ[n3](l)≐ϖ(l),   ε=(1,1,−1,1),(3.8e)
σ(l)=σ[n4](l)≐χ(l),   ε=(1,1,1,−1).(3.8f)

Note also that these vectors are related to ϕ(l) by

σ[ni](l)=A[ni]φ(l),   i=1,2,3,4,(3.9)
where
A[ni]=Diag((pi2−k12)−ni,(pi2−k22)−ni,…,(pi2−kN2)−ni),   i=1,2,3,4.(3.10)

In addition, it is remarkable that ϕ(l) composed by (3.1) is not the only vector that obeys the relation (3.6). One can easily find that taking ϕ1(l) from (3.1) and defining new φj(l)=∂k1j−1φ1(l) for j = 2, 3,...,N, ϕ(l) constructed in such a way satisfies (3.6) as well. More choices for ϕ(l) can be found in Sec. 3.3.

3.2. Bilinearization of (2.2) and Casoratian solutions

Under dependent variable transformations

S(a,b)=1a+b(1−θf),   V(a)=hf,   V(b)=sf,   w=gf,(3.11)
where
θ(a,b)=θ(b,a),   f(a,b)=f(b,a),(3.12)
system (2.2) is transformed into bilinear forms
ℋ11≡(p−a)θf˜−(p+b)θ˜f+(a+b)h˜s=0,(3.13a)
ℋ12≡(q−a)θf^−(q+b)θ^f+(a+b)h^s=0,(3.13b)
ℋ21≡(p−a)f˜^h−(q+a)fh˜^−(p+q)f^h˜=0,(3.13c)
ℋ22≡(p+a)fh˜^+(q−a)f˜^h−(p+q)f˜h^=0,(3.13d)
ℋ23≡(p+a)f^h˜−(q+a)f˜h^−(p−q)f˜^h=0,(3.13e)
ℋ31≡g^f˜−g˜f^+(p−q)(f^f˜−ff˜^)=0,(3.13f)
ℋ32≡gf˜^−g˜^f^+(p+q)(ff˜^−f^f˜)=0,(3.13g)
where (3.13f) and (3.13g) compose the bilinear lpKdV equation [14] and in the derivation of (3.13c)–(3.13e), we have made use of (3.13f) and (3.13g).

Casoratian solutions to bilinear system (3.13) can be summarized in the following Theorem.

Theorem 3.1.

The Casoratians

f=|N−1^|,   g=|N−2^,N|−Nf,   h=xT−αf,   s=yT−βf,   θ=xyT−αT−βf(3.14)
composed by ϕ(l), solve the bilinear system (3.13), where x and y are arbitrary nonzero constants and we require the basic column vector ϕ(l) satisfies shift relation (3.6) and assume there are invertible matrices A[ni] to define auxiliary vectors σ[ni](l) via (3.9) that obey shift relations (3.8). To meet the symmetric relation (3.12) and the assumption that V (a) is related to parameter a but independent of b, V(b) = V(a)|a→b and w is independent of (a, b), one needs to impose (3.14)|a=b=0.

Proof.

Due to the shift relation (3.6), the Casoratian |N−1^| can be defined in terms of shifts of any variable ni and they are same (refer to Eqs.(2.22) and (2.24) in [14]). For the Eqs. (3.13a)–(3.13e), with the notations in (3.14) and (3.5), they can be expressed as the following:

(pi−pj)f(TniTnjTnkf)−(pi+pk)(Tnif)(TnjTnkf)+(pj+pk)(Tnjf)(TniTnkf)=0,(3.15)
where i, j, k ∈ {1, 2, 3, 4}, i ≠ j ≠ k. For a certain triplet {ni, nj, nk}, this is the well known Hirota-Miwa equation [18]. It is also one of bilinear equations of H3 (see (5.20a,b) in [14]). Thus the proof for (3.15) under the condition of Theorem 3.1 has been given in [24].

The bilinear lpKdV equations (3.13f) and (3.13g) can be proved following the procedure given in [27] where the case c = 0 was handled. Here we only prove (3.13f), and the other can be treated similarly. The down-tilde-hat version of ℋ31 is

ℋ̂˜31≡[(p−f)f˜+g˜]f̂−[(q−c)f̂+ĝ]f˜−(p−q)ff̂˜=0.(3.16)

For (p−c)f˜+g˜, f̂, (q−c)f̂+ĝ, f˜ and (p−q)f̂˜, we use (B.1b) and (B.1a) with i = 2, respectively, i = 1 and (B.1c) with i = 1, j = 2. Then we have

ℋ̂˜31≡[(p−c)f˜+g˜]f̂−[(q−c)f̂+ĝ]f˜−(p−q)ff̂˜=1[(p−c)(q−c)]N−2(|N−3^,N−1,T−nφ(N−2)||N−2^,T−mφ(N−2)|−|N−3^,N−1,T−mφ(N−2)||N−2^,T−nφ(N−2)|−|N−3^,T−mφ(N−2),T−nφ(N−2)||N−1^|)=0,
where we have utilized Lemma 3.1, in which G=N−3^, (a, b, c, d) = (ϕ(N − 1), T−nϕ(N − 2), ϕ(N − 2), T−mϕ(N − 2)).

3.3. Solutions for system (3.6) and (3.8)

Note that system (3.6) and (3.8) with general invertible matrices A[ni] are difference equations for unknown functions ϕ(l) and σ[ni](l). Solutions for these systems can be classified according to the canonical forms of A[ni]. Let us list them out case by case.

3.3.1. Soliton solutions

When A[ni] are diagonal matrices defined as (3.10), we take ϕj(l) to be (3.1) and φj(l), ψj(l), ϖj(l), χj(l) to be (3.7). Parameters x and y in (3.14) are taken as

x=∏j=1N(a−kj),   y=∏j=1N(b−kj).(3.17)

This is the case to generate solitons.

There is a singularity for S(a, b) defined in (3.11) when b = −a. In the following, we define S(a, −a). For ϕj(l) given in (3.1) and x, y defined above, it is easy to check

limb→−af−θ=0.

Thus, by means of the L’Hopital rule, we can define

S(a,−a)=limb→−a∂b(f−θ)f|α=β=0.(3.18)

3.3.2. Jordan block solutions

To present elements of the basic Casoratian column vector of this case, we first introduce lower triangular Toeplitz (LTT) matrices which are defined as

𝒜=(a000⋯00a1a00⋯00a2a1a0⋯00⋮⋮⋯⋮⋮⋮aN−1aN−2aN−3⋯a1a0)N×N,   aj∈ℂ.

Note that all the LTT matrices of same order compose a commutative set in terms of matrix product. Canonical form of such a matrix is a Jordan matrix. LTT matrices play an important role in generating multiple-pole (or limit) solutions (cf. [25, 26, 30, 31]).

When A[ni] takes a LTT form

A[ni]=(γs,j)N×N,   γs,j={1(s−j)!∂ks−j(pi2−k2)−ni,s≥j,0,s<j,(3.19)
the vector ϕ(l) that is used to construct Casoratians can be taken as
φ(l)=𝒜+φ+(l,k)+𝒜−φ−(l,k)(3.20a)
with
φ+(l,k)=(φ0±(l,k),φ1±(l,k),…,φN−1±(l,k))T,(3.20b)
φs±(l,k)=1s!∂ks[ρ±(p±k)n(q±k)m(a±k)α(b±k)β(c±k)l],(3.20c)
where ρ± ∈ ℂ, 𝒜± are two arbitrary LTT matrices of N-th order. Accordingly, auxiliary vectors σ[ni](l) are defined through (3.9).

It is known that Jordan block solutions can be understood as limit solutions of solitons (cf. [26]).b Employing a same limit procedure on the soliton case of Sec. 3.3.1, we can find in this case that

x=(a−k)N,   y=(b−k)N,(3.21)
and S(a, −a) is given by (3.18) but now with column vector (3.20).

3.3.3. Rational solutions

Rational solutions are formally generated from Jordan block solutions by taking k = 0 in (3.20a) and (3.19). However, to avoid trivial solutions, in practice we do the following. Consider a generating function

φ(l,k)=φ+(l,k)+φ−(l,k),   φ±(l,k)=ρ±(p±k)n(q±k)m(a±k)α(b±k)β(c±k)l,(3.22)
and expand ϕ(l, k) in terms of k at k = 0, where in practice we usually replace (c ± k)l with (c ± k)l+l0 and suppose that l0 is either an integer large enough or a non-integer so that the derivative ∂ks(c+k)l+l0|k=0≠0.

In special cases when ρ+ = −ρ− the generating function ϕ(l, k) is an odd function of k and the remained in its expansion are only odd order terms of k. We denote coefficients of these terms by

ηj=2j!∂kjφ+|k=0,   j=0,1,2,….(3.23)

Then Casoratian column ϕ(l) for rational solutions can be taken as

φ(l)=φ+(l)=(η1,η3,η5,….η2N−1)T,(3.24)

A[ni] = (γs,j)N×N is taken as

γs,j={1(2(s−j))!∂k2(s−j)(pi2−k2)−ni|k=0,s≥j,0,s<j,(3.25)
and those auxiliary vectors σ[ni](l) are defined through (3.9) accordingly. When ρ+ = ρ− one can also take
φ(l)=φ−(l)=(η0,η2,η4,….η2N−2)T,(3.26)
and in this case matrix A[ni] is still defined through (3.25) and σ[ni](l) are defined through (3.9). Since both cases share a same A[ni], a more general choice for ϕ(l) can be
φ(l)=𝒜+φ+(l)+𝒜−φ−(l),(3.27)
where ϕ±(l) are defined in (3.24) and (3.26), and 𝒜± are two arbitrary LTT matrices of N-th order.

In this case, parameters x and y are

x=aN,   y=bN,(3.28)
and S(a,−a) is still given in the form (3.18) but with column vector (3.27).

3.3.4. Rational solutions: revisit

It will be interesting to have a close look at the explicit formulae of ηj defined through (3.23). For more convenience we consider vector

φ′(l)=(φ1′(l),φ2′(l),…,φN′(l))T(3.29)
with
φj′(l)=p−nq−ma−αb−βφj(l)=ρj+(1+kj/p)n(1+kj/q)m(1+kj/a)α(1+kj/b)β(1+kj)l   +ρj−(1−kj/p)n(1−kj/q)m(1−kj/a)α(1−kj/b)β(1−kj)l,(3.30)
where ϕj(l) is defined in (3.1) but here we take c = 1 in this mini section. Denote Casoratians |N−1^| and |N−2^,N| composed by the above ϕ′(l) by f′ and g′ + Nf′, respectively. Then, compared with those Casoratians f and g that are composed by (3.1) with c = 1, we have
f=(pnqmaαbβ)Nf′,   g=(pnqmaαbβ)Ng′.(3.31)

Due to gauge property of discrete Hirota bilinear equations (cf. [14, 15]), both (f, g) and (f′, g′) solve bilinear equations (3.13). Consequently, system (2.2) admits an alternative expressions for soliton solutions

S(a,b)=1a+b(1−θ′f′),   V(a)=h′f′,   V(b)=s′f′,   w=g′f′,(3.32)
where f′ and g′ are defined through (3.31),
h′=x′T−αf′,   s′=y′T−βf′,   θ′=x′y′T−αT−βf′,   x′=1aN∏j=1N(a−kj),   y′=1bN∏j=1N(b−kj),(3.33)
with finally taking α = β = 0. For S(a, −a),
S(a,−a)=limb→−a∂b(f′−θ′)f′|α=β=0.(3.34)

With regard to rational solutions, we start from (3.30) with a general k, i.e.

φ′(l,k)=φ′+(l,k)+φ′−(l,k),   φ′±(l,k)=ρ±(1±kp)n(1±kq)m(1±ka)α(1±kb)β(1±k)l,(3.35)
where we specially take
ρ±=±12exp[−∑j=1∞(∓k)jjγj](3.36)
with arbitrary constants γj, and we expand ϕ′±(l, k) as
φ′+(l,k)=±12∑j=0∞ηj±kh,   ηj±=±2j!∂kjφ′+|k=0.(3.37)

Similar to the treatment in [28], we rewrite ϕ′±(l, k) as

φ′+(l,k)=±12exp[−∑j=1∞(∓k)jjxˇj],(3.38)
where
xˇj=xj+l,   xj=npj+mqj+αaj+βbj+γj.(3.39)

Then by comparison of (3.37) and (3.38), we can find all {ηj±} can be expressed in terms of {xj}. The formula is given by (cf. [28])

ηj±≐ηj±(n,m,α,β,l)=(∓1)j∑‖μ‖=j(−1)|μ|xˇμμ!(3.40)
where
μ=(μ1,μ2,…),   μj∈{0,1,2,…},   ‖μ‖=∑j=1∞jμj,|μ|=∑j=1∞μj,   μ!=μ1!⋅μ2!⋯,   xˇμ=(xˇ11)μ1(xˇ22)μ2⋯.

Explicit forms of some ηj+ are

η0+=1,   η1+=xˇ1,   η2+=12(xˇ12−xˇ2),   η3+=16(xˇ13−3xˇ1xˇ2+2xˇ3),η4+=124(xˇ14−6xˇ12xˇ2+8xˇ1xˇ3+3xˇ22−6xˇ4),η5+=1120(xˇ15−10xˇ2xˇ13+20xˇ3xˇ12+15xˇ22xˇ1−30xˇ4xˇ1−20xˇ2xˇ3+24xˇ5).

With these results in hand, let us summarize rational solutions of the system (2.2) by the following Theorem.

Theorem 3.2.

Define

φodd′(l)=(η1+,η3+,,….,η2N−1+)T,(3.41a)
φeven′(l)=(η0+,η2+,,….,η2N−2+)T,(3.41b)
φ′(l)=𝒜+φodd′(l)+𝒜−φeven′(l),(3.41c)
where {ηj+} are defined in (3.40), and 𝒜± are two arbitrary LTT matrices of N-th order. Then, rational solutions of the system (2.2) are expressed by (3.32), where
f′=f′(φ′(l))=|N−1^|,   g′=g′(φ′(l))=|N−2^,N|−Nf′(3.42a)
are Casoratians composed by (3.41c),
h′=T−αf′,   s′=T−βf′,   θ′=T−αT−βf′,(3.42b)
and finally we need to take α = β = 0 in (3.42). S(a, −a) is defined by
S(a,−a)=limb→−a∂b(f′−θ′)f′|α=β=0.(3.43)

We remark that in special case f′(ϕ′odd(l)) leads to a rational solution one order higher than f′(ϕ′even(l) does (see Lemma 5.4 in Ref. [28]). Here we write out explicit forms of some f′ and g′ composed by ϕ′odd(l) without any restriction on α, β:

fN=1′(φodd′(l))=x1,   gN=1′(φodd′(l))=1,(3.44a)
fN=2′(φodd′(l))=x13−x33,   gN=2′(φodd′(l))=x12,(3.44b)
fN=3′(φodd′(l))=145x16−19x13x3+15x1x5−19x32,   gN=3′(φodd′(l))=215x15−13x12x3+15x5.(3.44c)

A second remark is presented through the following Proposition.

Proposition 1.

For the Casoratian f′(ϕ′odd(l)), the following relations hold:

∂x1f′(φodd′(l))=g′(φodd′(l))=|N−2^,N|−Nf′(φodd′(l)),(3.45a)
∂x12f′(φodd′(l))=−N2f′(φodd′(l))−2Ng′(φodd′(l))+ζ′(φodd′(l)),(3.45b)
where
ζ′(φodd′(l))=|N−2^,N+1|+|N−3^,N−1,N|.(3.45c)

Proof.

For ϕ′+(l, k) defined in (3.35), it is easy to see

φ′+(l+1,k)−φ′+(l,k)=kφ′+(l,k).(3.46)

It then follows from (3.37) and (3.38) that

ηj+(l+1)−ηj+(l)=ηj−1+(l),   (j≥1)(3.47)
and
∂x1ηj+(l)=ηj−1+(l),   (j≥1),(3.48)
and consequently we have
∂x1ηj+(l)=ηj+(l+1)−ηj+(l),   (j≥1),(3.49)
which leads to
∂x1φodd′(l)=φodd′(l+1)−φodd′(l),(3.50)
and moreover
∂x12φodd′(l)=φodd′(l+2)−2φodd′(l+1)+φodd′(l).(3.51)

Making use of these relations, (3.45) can be verified directly.

We also remark that some properties of f′(ϕ′odd(l)) can be found in Theorem C.2 in Appendix C of Ref. [28]. One of the properties is:

Proposition 2.

f′(ϕ′odd(l)) is a polynomial of {x1, x3,...,x2N−1} and coefficients are independent of {p, q, a, b}. (So are g′(ϕ′odd(l)) and ζ′(ϕ′odd(l)) due to Proposition 1.)

Thanks to such a property, S(a, −a) is well defined by the formula

S(a,b)=1a−b(1−T−αT−βf′f′|)|α=β=0.(3.52)

In fact, write f′ = f′[x] = f′[x1, x3,...,x2N−1]. Then we have

T−αT−βf′[x]=f′[x−ε]=f′[x1−ε1,x3−ε3,…,x2N−1−ε2N−1],
where
ε2j−1=1a2j−1+1b2j−1.(3.53)

By Taylor expanding T−aT−b f′[x] at (ε1,...,ε2N−1) = (0,...,0), we have

T−αT−βf′[x]=f′[x−ε]=f′[x]−∑j=12N−1ε2N−j∂x2N−jf′[x]+12!∑j=12N−1∑i=12N−1ε2N−jε2N−i∂x2N−j∂x2N−if′[x]+⋯.(3.54)

Noticing that each ε2j−1 has a factor a + b, i.e.

ε2j−1a+b=ν2j−1=1a2j−1b2j−1∑i=02(j−1)(−1)ia2(j−1)−ibi,(3.55)
after substituting (3.54) into (3.52), it is easy to see that the term a + b in the denominator of (3.52) can be eliminated and as a definition (3.52) is valid to S(a, −a).

The first two rational solutions of the NQC equation (2.1) are

S(a,b)=1abz1,(3.56a)
S(a,b)=3(az1−1)(bz1−1)a2b2(z13−z3),(3.56b)
where
zj=xj|α=β=0=npj+mqj+γj.(3.57)

Rational solutions of Q3δ (1.1a) are given by (2.5), where Ϝ(a, b) is defined in (2.6) and A, B, C, D obey the constraint (2.7). The first two rational solutions of Q3δ are

u=AϜ(a,b)[1−a+babz1]+BϜ(a,−b)[1+a−babz1]+CϜ(−a,b)[1−a−babz1]+DϜ(−a,−b)[1+a+babz1],(3.58a)
u=AϜ(a,b)[1−3(a+b)(az1−1)(bz1−1)a2b2(z13−z3)]+BϜ(a,−b)[1+3(a−b)(az1−1)(bz1+1)a2b2(z13−z3)]+CϜ(−a,b)[1+3(b−a)(az1+1)(bz1−1)a2b2(z13−z3)]+DϜ(−a,−b)[1+3(a+b)(az1+1)(bz1+1)a2b2(z13−z3)].(3.58b)

4. Degeneration of rational solutions

We now consider the problem of degeneration of rational solutions of Q3δ down to those of the “lower” equations Q2, Q1δ, H3δ, H2 and H1 in the ABS list (1.1). To do so we follow the degenerations given in Ref. [19] which are limits on the parameters a and b and the dependent variable u, where a small parameter ε is introduced, and all degenerations are obtained in the limit ε → 0. The degeneration relations between Q3δ and the “lower equations” are depicted as Fig.1 [19].

Fig. 1.

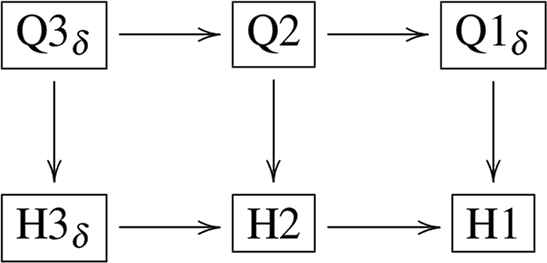
Degeneration relation

4.1. Q3δ −→ Q2

The degeneration from Q3δ to Q2 is implemented through taking

b=a(1−2ε),   u→δ4a2(1ε+1+(1+2u)ε).(4.1)
and making the following replacements of constants in (2.5),
A→δ4a2Aε,   B→δ8a2(1ε+1−ξ0+((3+ξ02)/2+2AD)ε),C→δ8a2(1ε+1+ξ0+((3+ξ02)/2+2AD)ε),   D→δ4a2Dε.(4.2)

Then, rational solutions for Q2 are given as

u=14((ξ+ξ0)2+1)+a(ξ+ξ0)S(−a,a)+a2(Z(a,−a)+Z(−a,a))+AD+12Aρ(a)(1−2aS(a,a))+12Dρ(−a)(1+2aS(−a,−a)),(4.3)
in which
ξ=2a(pa2−p2n+qa2−q2m),   Z(a,−a)=−∂bS(a,b)|b=−a,   Z(a,−a)=Z(a,−a)|a→−a,(4.4)
and ξ0, A and D are arbitrary constants; ρ(a) is defined by (A.10). In (4.4), when N = 1 and N = 2, we have
Z(a,−a)=1a3z1,(4.5a)
Z(a,−a)=3z13(az1−1)(az1+2)−3(a+a2z1−2)z3a5(z13−z3)2,(4.5b)
where zj is defined by (3.57). However, it is hard to give an explicit formula for Z(a, −a) in terms of Casoratians.

Pure rational solutions of Q2 are obtained by taking A = D = 0. The first two of them are

u=14((ξ+ξ0)2+1)−1az1(ξ+ξ0),(4.6a)
u=14((ξ+ξ0)2+1)−a2z12−13a3(z13−z3)(ξ+ξ0)+6z14−z3a2(z13−z3)2.(4.6b)

4.2. Q2 −→ Q1δ

To achieve rational solutions for Q1δ, consider degeneration of (4.3) by taking

u→δ24ε2+1εu.

Meanwhile, we replace the constants appearing in solution (4.3) by

A→2Aε,   D→2Dε,   ξ0→ξ0+2Bε.(4.7)

Then the rational solutions for Q1δ can be described as

u=Aρ(a)(1−2aS(a,a))+B(ξ+ξ0+2aS(−a,a))+Dρ(−a)(1+2aS(−a,−a)),(4.8)
where ρ(a) is defined by (A.10) and constants A, B, D are chosen to satisfy the constraint
AD+14B2=δ216.(4.9)

Some explicit S(a, b) can be seen from (3.56). The first two solutions given by (4.8) are

u=Aρ(a)(1−2az1)+B(ξ+ξ0−2az1)+Dρ(−a)(1+2az1),(4.10a)
u=Aρ(a)(1−6(az1−1)2a3(z13−z3))+B(ξ+ξ0−6a2z12−1a3(z13−z3))+Dρ(−a)(1+6(az1+1)2a3(z13−z3)).(4.10b)

4.3. Q3δ −→ H3δ

By setting

b=1ε2,   u→ε3δ2u,(4.11)
and
A→ε3δ2A,   B→ε3δ2B,   C→ε3δ2C,   D→ε3δ2D,(4.12)
rational solutions to H3δ can be obtained from (2.5) and take the form
u=(A+(−1)n+mB)ϑV1(a)+((−1)n+mC+D)ϑ−1V1(−a),(4.13)
in which V1(±a) come from Taylor expressions:
1−(a+b)S(a,b)→V1(a)+O(ε2),1−(a−b)S(a,−b)→V1(a)+O(ε2),1+(a−b)S(−a,b)→V1(−a)+O(ε2),1+(a+b)S(−a,−b)→V1(−a)+O(ε2),(4.14)
and
ϑ=(Pa−p)n(Qa−q)m,(4.15)
where P, Q are defined by (1.3) and constants A, B, C and D are subject to the constraint
AD−BC=δ4a.

Let us have a close look at V1(a). Considering S(a, b) defined by (3.52), which is valid for b = −a as well, we find

1−(a+b)S(a,b)=T−αT−βf′[x]f′[x]|α=β=0.(4.16)

Since f′[x] is a polynomial of {x1, x3,...,x2N−1}, (see Proposition 2), substituting b=1ε2 and after taking ε → 0, all the terms of 1bj vanish, i.e. all the shifts with respect to β do not make sense any longer. Thus, we immediately reach

V1(a)=T−αf′[x]f′[x]|α=β=0.(4.17)

When N = 1, V1(a) reads

V1(a)=1−1az1,
and when N = 2, V1(a) is
V1(a)=1−3z1(az1−1)a2(z13−z3).

The first two solutions of H3δ are

u=(A+(−1)n+mB)ϑ(1−1az1)+((−1)n+mC+D)ϑ−1(1+1az1),(4.18a)
u=(A+(−1)n+mB)ϑ(1−3z1(az1−1)a2(z13−z3))+((−1)n+mC+D)ϑ−1(1+3z1(az1+1)a2(z13−z3)).(4.18b)

4.4. Q2 −→ H2

The degeneration from Q2 to H2 can be obtained by setting

a=1ε,   u→14+ε2u.(4.19)

Substituting (4.19) into (4.3), combined with

a2S(−a,a)→−S(0)+O(ε),a2S(a,a)→S(0)−2εS(1)+O(ε2),a2S(−a,−a)→S(0)+2εS(1)+O(ε2),a2(Z(−a,a)+Z(a,−a))→2εS(1)+O(ε2),(4.20)
and the following choice for the constants
A→A(ε+(γ′+2γ−1)ε2),   D→A(−ε+(γ′+2γ−1)ε2),   ξ0→2εγ−1(4.21)
with unconstrained constants γ′, γ−1, rational solutions for H2 can be obtained, which are given by
u=z−12−2z−1S(0)+2S(1)−A2+(−1)n+mA(2z−1+γ′−2S(0)).(4.22)

In the following we derive explicit Casoratian forms for S(0) and S(1). For convenience we take f′ = f′(ϕ′odd(l)). Recalling the analysis for f′ in Sec. 3.3.4, noticing Taylor expansion (3.54) and relation (3.55), we have

a2S(a,b)=a2f′[z](∑j=12N−1ν2N−j∂z2N−jf′[z]−12!∑j=12N−1∑i=12N−1ν2N−jε2N−i∂z2N−j∂z2N−if′[z]+⋯),(4.23)
where f′[z] = f′[z1, z3,...,z2N−1]. When taking a=1ε we have
a2S(a,−a)=−1f′[z](∂z1f′[z]+O(ε2)).

Thus, compared with (4.20) and making use of Proposition 1, yield

S(0)=g′[z]f′[z]=|N−2^,N||N−1^|−N.(4.24)

The case of S(a, a) is little bit complicated. Let εj′=α−1aj−β−1bj. Then T−aT−bf′[x] can be written as

T−αT−βf′[x]=f′[z]+∑j=12N−1ε2N−j′∂z2N−jf′[z]+12!∑j=12N−1∑i=12N−1ε2N−j′ε2N−i′∂z2N−j∂z2N−if′[z]+⋯.

Taking b=a=1ε and then β = α = 0 yields

T−αT−βf′[x]|β=α=0=f′[z]−2ε∂z1f′[z]+2ε2∂z12f′[z]+⋯.

Then we have

a2S(a,−a)=∂z1f′[z]f′[z]−ε∂z12f′[z]f′[z]+O(ε2),
where we have taken a=1ε. After a comparison with (4.20) and making use of Proposition 1, we reach
S(1)=12∂z12f′[z]f′[z]=−Ng′[z]f′[z]+ζ′[z]2f′[z]−N22=12|N−3^,N−1,N|+|N−2^,N+1|−2N|N−2^,N||N−1^|+N22.(4.25)

The first two S(0) are

S(0)=1z1   and   S(0)=3z12z13−z3.(4.26)

The first two S(1) are

S(1)=0   and   S(1)=3z1z13−z3.(4.27)

And the first two rational solutions of H2 are

u=z−12−2z−1z1−A2+(−1)n+mA(2z−1+γ′−2z1),(4.28a)
u=z−12+6z1(1−z−1z1)z13−z1−A2+(−1)n+mA(2z−1+γ′−6z12z13−z3).(4.28b)

4.5. Q1δ −→ H1

The rational solution to H1 can be obtained from (4.8) through degeneration. Substituting

a=1ε,   u→εδu(4.29)
into (4.8) and using
A→δ2A(1+2(γ′+γ−1)ε),   D→δ2A(−1+2(γ′+γ−1)ε),   B→δB,   ξ0→2εγ−1(4.30)
with constants γ′, γ−1, we have
u=B(z−1−S(0))+(−1)n+mA(z−1+γ′−S(0)),(4.31)
which presents rational solutions of H1, where γ′, A and B satisfy A2 − B2 = −1. Here S(0) is same as the one in solution (4.22). The first two rational solutions given by (4.31) are
u=B(z−1−1z1)+(−1)n+mA(z−1+γ′−1z1),(4.32a)
u=B(z−1−3z12z13−z3)+(−1)n+mA(z−1+γ′−3z12z13−z3).(4.32b)

5. Conclusions

In this paper we have derived solutions in terms of Casoratians for the NQC equation. It turns out that the τ-function f with auxiliary directions (α, β) satisfies the Hirota-Miwa equations that are defined in any three directs of (n, m, α, β), but finally (α, β) are restricted to be (0,0). This indicates that, with regard to generating soliton solutions for the ABS equations (except Q4), the Hirota-Miwa equation acts as a master equation to govern the τ-function f.

Rational solutions of the NQC equation are obtained by considering the case that auxiliary matrices A[ni] take the form (3.25) with k = 0. Such rational solutions can be equivalently derived by taking “long-wave-limit”. In this paper, we examined the significance of our rational solutions in the Miura transformation (2.5) from the NQC equation to Q3δ and in the degenerations from Q3δ to the “lower” equations in the ABS list. As a result, we obtained rational solutions in terms of Casoratians for the NQC equation, Q3δ, Q1δ, H3δ, H2 and H1. However, for Q2 we did not find an explicit form of Z(a, −a) in terms of Casoratians. This will be considered in the future. Besides, it is worthy to mention that {xj} defined through (3.38) play an important role in the analysis of rational solutions.

Compared with [28], one can find that some rational solutions of the ABS equations were obtained by means of Bäcklund transformations in [28] can not be derived in this paper. For example, for the rational solutions of Q1δ, (5.28c) in [28] can not be obtained from (4.8) of the present paper, and vice versa.

A further remark is about solving the NQC equation (2.1). In this paper we solve the equation through solving the system (2.2) that contains the lpKdV equation and two Miura transformations, and is based on the Cauchy matrix scheme that provides many clues for bilinearisation. This system is also used in deriving the Miura transformation (2.5) between the NQC equation and Q3δ (see Appendix A). In some sense, (3.13a–3.13e) can be viewed as a bilinear form of the NQC equation. If we only solve the NQC equation, (2.2a, 2.2b) together with extensions in α-and β-direction are enough (cf. Sec. 9.5.3 in [13]). Note that (2.2a, 2.2b) can be considered as a generalisation (with parameters (a, b)) of the class of Bäcklund transformations investigated in [29] (see (3.1) with (3.5) in [29]). This motivates us to reconsider [29] with parameters, which will be done in the future.

Appendix A. Proof of Theorem 2.1

Proof.

The proof is similar to the one given in Ref. [19]. We need three steps. Let us proceed them step by step.

Step # 1. We first introduce a new associated dependent variable U that is given by:

U=(a+b)AϜ(a,b)V(a)V(b)+(a−b)BϜ(a,−b)V(a)V(−b)−(a−b)CϜ(−a,b)V(−a)V(b)−(a+b)DϜ(−a,−b)V(−a)V(−b).(A.1)

Lemma A.1.

For u defined in (2.5) and the associated variable U defined in (A.1) the following hold:

p−q+w^−w˜=1U[Pu˜−Qu^−(p2−q2)u](A.2a)
=−1U˜^[Pu^−Qu˜−(p2−q2)u˜^],(A.2b)
p+q+w−w˜^=1U^[Pu˜^−Qu−(p2−q2)u^](A.2c)
=−1U˜^[Pu−Qu˜^−(p2−q2)u˜],(A.2d)
where w satisfies system (2.2). The relations (A.2) hold for arbitrary coefficients A, B, C, D.

Proof.

We denote u and U, respectively, defined by (2.5) and (A.1) as

u=uA(a,b)+uB(a,−b)+uC(−a,b)+uD(−a,−b),(A.3a)
U=UA(a,b)+UB(a,−b)+UC(−a,b)+UD(−a,−b),(A.3b)
where uA(a, b) = AϜ(a, b)[1 − (a + b)S(a, b)] and UA(a, b) = (a + b)AϜ(a, b)V(a)V(b). By direct computation, we get
P(uA(a,b))~−Q(uA(a,b))^−(p2−q2)uA(a,b)=AϜ(a,b)[(p+a)(p+b)(1−(a+b)S˜(a,b))   −(q+a)(q+b)(1−(a+b)S^(a,b)−(p2−q2)(1−(a+b)S(a,b))]=A(a+b)Ϝ(a,b)[(p−q)−(p+a)(p+b)S˜(a,b)   +(q+a)(q+b)S^(a,b)+(p2−q2)S(a,b)]=A(a+b)Ϝ(a,b)[(p+a)(1−(p+b)S˜(a,b)+(p−a)S(a,b))      −(q+a)(1−(q+b)S^(a,b)+(q−a)S(a,b))]=A(a+b)Ϝ(a,b)[(p+a)V˜(a)V(b)−(q+a)V^(a)V(b)]=A(a+b)Ϝ(a,b)(p−q+w^−w˜)V(a)V(b)=(p−q+w^−w˜)UA(a,b),(A.4)
where relations (2.2a), (2.2b) and (2.2d) have been used. In terms of symmetric property, we also havex
   P(uB(a,−b))~−Q(uB(a,−b))^−(p2−q2)uB(a,−b)=(p−q+w^−w˜)UB(a,−b),(A.5a)
   P(uC(−a,b))~−Q(uC(−a,b))^−(p2−q2)uC(−a,b)=(p−q+w^−w˜)UC(−a,b),(A.5b)
   P(uD(−a,−b))~−Q(uD(−a,−b))^−(p2−q2)uD(−a,−b)=(p−q+w^−w˜)uD(−a,−b).(A.5c)

By adding the four equations in (A.4) and (A.5), we arrive at (A.2a). Similar analysis can be done to (A.2b)–(A.2d).

Step # 2.

Lemma A.2.

The following identities hold

UU˜−P(u2+u˜2)+(2p−a2−b2)uu˜=4abPdet(𝒜),(A.6a)
UU^−Q(u2+u^2)+(2q2−a2−b2)uu^=4abQdet(𝒜),(A.6b)
in which the 2 × 2 matrix 𝒜 is given by
𝒜=((a+b)A(a−b)B−(a−b)C−(a+b)D)(A.7)
provided that S(±a, ±b), v(±a) and v(±b) satisfy the system (2.2) together with symmetry S(a, b) = S(b, a) with parameters ±a, ±b.

Proof.

We consider the following 2 × 2 matrices:

L=(Pu˜−(p2−b2)u(p−b)U(p+b)U˜−Pu+(p2−b2)u˜),(A.8a)
M=(Qu^−(q2−b2)u(q−b)U(q+b)U^−Qu+(q2−b2)u^).(A.8b)

Evaluating the entries in these matrices we obtain

Pu˜−(p2−b2)u=AϜ(a,b)[P2(p−a)(p−b)(1−(a+b)S˜(a,b))−(p2−b2)(1−(a+b)S(a,b))]+…=AϜ(a,b)(p+b)[(p+a)(1−(a+b)S˜(a,b))−(p−b)(1−(a+b)S(a,b))]+…=AϜ(a,b)(p+b)(a+b)[1−(p+a)S˜(a,b)+(p−b)S(a,b)]+…=A(a+b)Ϝ(a,b)(p+b)V˜(b)V(a)+…=p2−b2rT(a)𝒜r˜(b),(A.9)
in which again the dots in each line on the right hand sides stand for similar terms with (a, b) replaced by (a, −b), (−a, b), (−a, −b) and A replaced by B, C, D respectively. On the right-hand side of this expression we have introduced vectors
r(a)=(ρ1/2(a)V(a)ρ1/2(−a)V(−a)),   rT(b)=(ρ1/2(b)V(b),ρ1/2(−b)V(−b)),
in which the plane-wave factor ρ(a) is given byx
ρ(a)=(p+ap−a)n(q+aq−a)m.(A.10)

A similar computation as above yields

−Pu+(p2−b2)u˜=p2−b2r˜T(a)𝒜r(b),(A.11)
whilst U and Ũ can be written as
U=rT(a)𝒜r(b),    U˜=r˜T(a)𝒜r˜(b).(A.12)

Thus, we find that the matrix L in (A.8) can be written as

L=(p2−b2rT(a)𝒜r˜(b)(p−b)rT(a)𝒜r(b)(p+b)r˜T(a)𝒜r˜(b)p2−b2r˜T(a)𝒜r(b)),
and similarly for the matrix M. Using now the general determinantal identity
det(∑j=1rxjyjT)=det((yjT⋅xj)i,j=1,…,r)
for any collection of r pairs of r-component column vectors xi, yi (the superindex T denoting transposition), we obtain the following result:
det(L)=(p2−b2)det(𝒜r˜(b)rT(a)+𝒜r(b)r˜T(a))=(p2−b2)det(r˜(b)rT(a)+r(b)r˜T(a))=(p2−b2)det(𝒜)det{r˜(b)r(b)(rT(a)r˜T(a))}=−(p2−b2)det(𝒜)det(r(a),r˜(a)detr(b),r˜(b)).

It remains to compute the determinant of matrix (r(a),r˜(a)) whose columns are the 2-component vectors r(a) and r˜(a). This is done as follows

det(r(a),r˜(a))=ρ1/2(a)ρ˜1/2(−a)V(a)V˜(−a)−ρ˜1/2(a)ρ1/2(−a)V˜(a)V(−a)=p−ap+aV(a)V˜(−a)−p+ap−aV˜(a)V(−a)=p−ap+a[1−(p+a)S˜(a,−a)+(p+a)S(a,−a)]   −p+ap−a[1−(p−a)S˜(−a,a)+(p−a)S(−a,a)]=−2ap2−a2,
where we have used the fact that S(a, b) = S(b, a). Thus, putting everything together we obtain the result:
det(L)=−(p2−b2)det(𝒜)4abp2−a2p2−b2.(A.13)

On the other hand, a direct computation of the determinant gives:

det(L)=−[Pu˜−(p2−b2)u][Pu−(p2−b2)u˜]−(p2−b2)UU˜=−(p2−b2)[P(u2+u˜2)−(2p2−a2−b2)uu˜−UU˜].(A.14)

Comparing the two expressions for det(L) from (A.13) and (A.14) we obtain the first equation in Lemma A.2.

Step # 3. The last step is by combining the relations (A.2) and (A.6) as well as the lpKdV equation (2.2g) to assert that u solves the Q3δ equation. In fact, multiplying for instance (A.2b) by (A.2d) and using (A.6b), where we identify

det(𝒜)=δ216ab
according to (2.7), we obtain from the lpKdV equation:
p2−q2=(p+q+w−w˜^)(p−q+w^−w˜)=1U˜U˜^[Pu^−Qu˜−(p2−q2)u˜^][Pu−Qu˜^−(p2−q2)u˜]⇒(p2−q2)[Q(u˜2+u˜^2)−(2q2−a2−b2)u˜u˜^+δ24Q]=P2(uu^)+Q2(u˜u˜^)+(p2−q2)2u˜u˜^−PQ(uu˜+u^u˜^)−(p2−q2)P(u^u˜+uu˜^)+(p2+q2)Q(u˜2+u˜^2)=P2(uu^+u˜u˜^)+(Q2−P2)(u˜u˜^)+(p2−q2)2u˜u˜^−PQ(uu˜+u^u˜^)−(p2−q2)P(u^u˜+uu˜^)+(p2+q2)Q(u˜2+u˜^2)⇒(p2−q2)[−(2q2−a2−b2)u˜u˜^+δ24Q]=P[P(uu^+u˜u˜^)−Q(uu˜+u^u˜^)−(p2−q2)2(u^u˜+uu˜^)]+(p2−q2)[(a2+b2−p2−q2)u˜u˜^+(p2−q2)u˜u˜^],
where we have used the fact that 𝔭, 𝔮 are on the elliptic curve (1.2) and the identification of U˜U˜^ via the result (A.6) of Lemma A.2. From the last step, after some cancellation of terms, we obtain Q3δ, in the form (1.1a), for the function u, which completes the proof of the theorem.

Appendix B. Casoratian shift formulae

We list some shift formulae for the Casoratians (3.14), where the basic column vector ϕ(l) satisfies shift relation (3.6) and auxiliary relations (3.9). For convenience, we introduce notations T¯niφ(l)=A[ni]Tni(A[ni]−1φ(l)) with i = 1, 2, 3, 4. These Casoratian shift formulae are

T−nif=−(pi−c)2−N|N−2^,T−niφ(N−2)|,(B.1a)
T−ni((pi−c)f+g)=−(pi−c)2−N|N−3^,N−1,T−niφ(N−2)|,(B.1b)
T−niT−nj(pi−pj)f=[(pi−c)(pi−c)]2−N|N−3^,T−njφ(N−2),T−njφ(N−2)|,(B.1c)
and
Tnif=(pi−c)2−N(Tni|A[ni]|)|A[ni]−1||N−2^,T¯niφ(N−2)|,(B.2a)
TniT−nj(pi+pj)f=1[(pi+c)(pj−c)]N−2(Tni|A[ni]|)|A[ni]−1||N−3^,Tnjφ(N−2),T¯niφ(N−2)|,(B.2b)
Tni(g−(pi−c)f)=(pi+c)2−N(Tni|A[ni]|)|A[ni]−1||N−3^,N−1,T¯niφ(N−2)|,(B.2c)
where i = 1, 2, 3, 4.

Acknowledgments

The authors are grateful to the referee for the invaluable comments. This project is supported by the NSF of China (Nos. 11401529, 11301483, 11371241, 11631007) and the NSF of Zhejiang Province (Nos. LY17A010024, LY18A010033).

Footnotes

a

We keep the variable l in the notation ϕ(l) since Casoratians are defined in terms of shifts in l.

b

One can consider solitons where we take ϕ1 to be (3.1) and take ϕj (where j ≥ 2) by just replacing k1 with kj in ϕ1. Then we expand kj = k1 + εj at εj = 0 and take limit εj → 0 in the rational forms (3.11) successively for j = 2, 3,...,N. As a result, we get Jordan block solutions. For more details one can refer to [26].

References

[10]W. Feng, S.L. Zhao, and Y. Shi, Rational solutions for lattice potential KdV equation and two semi-discrete lattice potential KdV equations, Z. Naturforsch, Vol. 71, No. 2)a, 2016, pp. 121-128.
[24]Y. Shi and D.J. Zhang, Rational solutions of the H3 and Q1 models in the ABS lattice list, SIGMA, Vol. 7, 2011, pp. 11. 046
[26]D.J. Zhang, Notes on solutions in Wronskian form to soliton equations: KdV-type, arXiv:nlin.SI/0603008, 2006, pp. 45.
[27]D.J. Zhang and J. Hietarinta, Generalized solutions for the H1 model in ABS list of lattice equations, Nonl. Mod. Math. Phys: Proceedings of the First International Workshop, AIP Conference Proceedings, Vol. 1212, 2010, pp. 154-161.
[28]D.D. Zhang and D.J. Zhang, Rational solutions to the ABS list: Transformation approach, SIGMA, Vol. 13, 2017, pp. 24. 078
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
Journal of Nonlinear Mathematical Physics
Volume-Issue
26 - 1
Pages
107 - 132
Publication Date
2021/01/06
ISSN (Online)
1776-0852
ISSN (Print)
1402-9251
DOI
10.1080/14029251.2019.1544793How to use a DOI?
Copyright
© 2019 The Authors. Published by Atlantis and Taylor & Francis
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Song-lin Zhao
AU  - Da-jun Zhang
PY  - 2021
DA  - 2021/01/06
TI  - Rational solutions to Q3δ in the Adler-Bobenko-Suris list and degenerations
JO  - Journal of Nonlinear Mathematical Physics
SP  - 107
EP  - 132
VL  - 26
IS  - 1
SN  - 1776-0852
UR  - https://doi.org/10.1080/14029251.2019.1544793
DO  - 10.1080/14029251.2019.1544793
ID  - Zhao2021
ER  -