Remarks on the mass spectrum of two-dimensional Toda lattice of E8 type
- DOI
- 10.1080/14029251.2020.1683961How to use a DOI?
- Abstract
A simple procedure for obtaining the mass spectrum of 2-dimensional Toda lattice of E8 type is given.
- Copyright
- © 2020 The Authors. Published by Atlantis and Taylor & Francis
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. Introduction. Basics
Let us recall several definitions; for more details, see the book [10].
Let 𝔤 be a simple Lie algebra of rank l, let R+ (resp. R−) be the set of its positive (resp. negative) roots, and {α1,...,αl} be the set of simple roots. Let W be the Weyl group of the root system R acting in the space V = ℝl, let (·,·) be the non-degenerate W-invariant bilinear form in V,
The 2-dimensional Toda lattice is 2-dimensional relativistic field theory describing l interacting scalar fields. The 2-dimensional Toda lattice is related with 𝔰𝔩 (n).
In the paper [8], the 2-dimensional Toda lattice was generalized for the case of any simple finite-dimensional Lie algebra 𝔤; it was shown that the generalized construction has remarkable integrability properties. This is a relativistic system with Lagrangian
The potential U(φ) is constructed using the set of simple roots
In [8], the mass spectrum of scalar fields was found for all simple Lie algebras, except for the most complicated case 𝔤 = E8. For this algebra only numerical result was given.
In this note I describe two simple methods for obtaining the mass spectrum in the E8 case. Note that both methods work also for any other finite-dimensional simple Lie algebra.
The numbering of simple roots of the Lie algebra E8 is given on the Dynkin diagram:
The Dynkin diagram for the Lie algebra E8.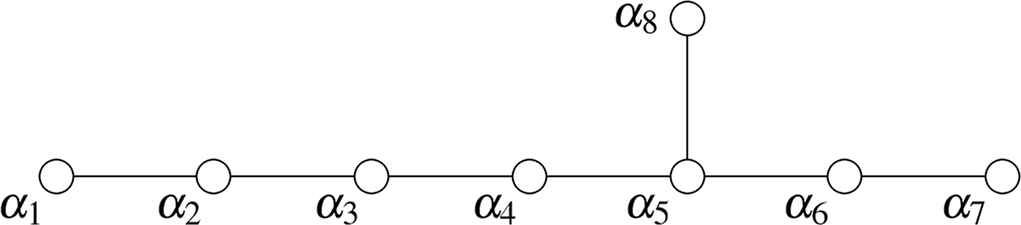
For this numbering, the highest root δ has the form
Observe that in 1989 A.B. Zamolodchikov discovered, using conformal theory, that this system appears also in the Ising model with nonzero magnetic field and explicitly calculated the mass spectrum, see [13]. The four mass ratios are equal to the “golden ratio”
This remarkable property is related to the fact that the Coxeter number h = 30 of the Lie algebra E8 is divisible by 5.
In 2010, Zamolodchikov’s theory was experimentally confirmed for 1-dimensional Ising ferro-magnet (cobalt niobate) near its critical point [2].
2. Method 1
As it was shown in papers [1, 5] the masses of particles are proportional to the components of a special eigenvector of the matrix A = 2I − C, where C is the Cartan matrix of 𝔤. This eigenvector is called the Perron–Frobenius vector, see [6, 12]. For 𝔤= E8, we have
The characteristic equation of this matrix is
Note also that x5 = −x4, x6 = −x3, x7 = −x2, x8 = −x1. Let us give the expressions of the xj in terms of radicals (these expressions might be used in calculations):
The matrix A has nonnegative elements and according to the Perron–Frobenius theorem [6, 12] it has a unique eigenvector (the Perron-Frobenius eigenvectors)
Solving the system of these equations, and fixing u1 = 2sin(θ), we obtain:
Note that from eq. (2.1) it follows that (recall that
This is a very nice solution, because these expressions for uj can be written immediately just by looking at the Dynkin diagram of E8.
Observe that for any simple Lie algebra the eigenvector corresponding to the maximal eigenvalue can also be written just by looking at the corresponding Dynkin diagram.
Let me also give expressions for some trigonometric quantities in terms of radicals (and use this occasion to correct a typo in the definition of H3 on p. 382 of [9], where
3. Method 2
In the paper [8] it was shown that the squares of masses are eigenvalues of the 8 × 8 matrix whose elements are
For the Lie algebra E8, the characteristic polynomial P of this matrix is
In the paper [1], it was observed that P = P1 P2, where
It is easy to check that the roots of polynomial P1 (resp. P2) are
Note that
The quantity
So, formula (3.1) gives a relation between methods 1 and 2.
Let me give also the explicit expression for quantities
4. Conclusion
The remarkable property of the system under consideration is that the four mass ratios in (2.2) are equal to the “golden ratio”.
This is one more phenomenon of many in which the golden ratio appears. The golden ratio has a very long history, see e.g., the book [4, Ch. 11]. The first book on this topic, “Divina Proportione”, illustrated by Leonardo da Vinci, was published by Italian mathematician Luca Paccioli in 1509 [11].
Concluding, I would like to give here a quotation of the outstanding astronomer and mathematician Johannes Kepler [7]: “Geometry has two treasures: one of them is the Pythagorean theorem, and the other is dividing the segment in average and extreme respect ... The first can be compared to the measure of gold; the second is more like a gem”.
Acknowledgments
I am thankful to D. Leites who improved my English in this article.
References
Cite this article
TY - JOUR AU - Askold M. Perelomov PY - 2019 DA - 2019/10/25 TI - Remarks on the mass spectrum of two-dimensional Toda lattice of E₈ type JO - Journal of Nonlinear Mathematical Physics SP - 12 EP - 16 VL - 27 IS - 1 SN - 1776-0852 UR - https://doi.org/10.1080/14029251.2020.1683961 DO - 10.1080/14029251.2020.1683961 ID - Perelomov2019 ER -
