Bayesian Deep Reinforcement Learning via Deep Kernel Learning
- DOI
- 10.2991/ijcis.2018.25905189How to use a DOI?
- Keywords
- Reinforcement learning; Uncertainty; Bayesian deep model; Gaussian process
- Abstract
Reinforcement learning (RL) aims to resolve the sequential decision-making under uncertainty problem where an agent needs to interact with an unknown environment with the expectation of optimising the cumulative long-term reward. Many real-world problems could benefit from RL, e.g., industrial robotics, medical treatment, and trade execution. As a representative model-free RL algorithm, deep Q-network (DQN) has recently achieved great success on RL problems and even exceed the human performance through introducing deep neural networks. However, such classical deep neural network-based models cannot well handle the uncertainty in sequential decision-making and then limit their learning performance. In this paper, we propose a new model-free RL algorithm based on a Bayesian deep model. To be specific, deep kernel learning (i.e., a Gaussian process with deep kernel) is adopted to learn the hidden complex action-value function instead of classical deep learning models, which could encode more uncertainty and fully take advantage of the replay memory. The comparative experiments on standard RL testing platform, i.e., OpenAI-Gym, show that the proposed algorithm outweighs the DQN. Further investigations will be directed to applying RL for supporting dynamic decision-making in complex environments.
- Copyright
- © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Reinforcement learning (RL)22, as an important branch of machine learning, aims to resolve the sequential decision-making under uncertainty problems where an agent needs to interact with an unknown environment with the expectation of optimising the cumulative long-term reward. A motivating example is the self-driving car. If we consider a car as the agent and the traffic conditions (e.g., traffic light signal and speed limitation) as the environment, RL can endow the car the ability to autonomously and safely choose actions (e.g., breaking, turning, and lighting) corresponding to difference traffic conditions when driving on road. Since the environment is unknown to the car, such ability needs to be learned through the so-called ‘trail-and-error’ strategy that is to learn an optimised action-selection policy through interacting with this environment4. Thus, there are two goals for the agent during the interaction with the environment: exploration which aims to perceive more about the environment and exploitation which aims to optimise the policy under current information about the environment. Apart from self-driving cars, many real-world tasks could be formalised as sequential decision-making under uncertainty problems and then benefit from RL, such as: industrial robotics9, medical treatment11, and trade execution14.
According to whether maintaining a computational model for the environment, existing RL algorithms could be categorised as being either model-based or model-free. Model-based RL algorithms improve the policy learning through modelling the environment, e.g., simulating the interactions with the environment model in hand or planning ahead using the model. Due to the lack of such environment model, model-free RL cannot infer the effect from environment dynamics and efficiently explore the space. However, for some complex environments with large scale states, it is too difficult to accurately build their models. Model-free RL algorithms directly learn the policy without requiring an explicit environment model. Recently, one seminal model-free RL algorithm, i.e., deep Q-network (DQN)13, has achieved great success on Atari games and substantially promote the development of RL. The advanced ability of DQN comes from two aspects: 1) deep learning models; DQN adopts deep neural networks to replace the traditional Q-table for the hidden action-value function learning. For complex environments with large or even near infinite number of states, Q-table is not appropriate due to the large-scale storage and high computation requirements; 2) experience replay; The historical interactions are saved as replay memory and sampled in DQN to stochastically update deep neural networks, which can reduce the dependency between sequential interactions and then increase the efficiency of the algorithm. However, the classical deep neural networks used in DQN cannot handle uncertainty well due to its deterministic nature. As defined, RL aims to handle sequential decision-making under uncertainty, so how to capture and deal with uncertainty is essential for RL. Besides, all the saved historical interactions are equally treated in DQN, but they are in fact different for model training and convergence.
In this paper, we propose a new model-free RL algorithm based on a Bayesian deep model - deep kernel learning28, which is able to encode more uncertainty and fully take advantage of the saved historical interactions. Specially, the deep kernel learning is a Gaussian process (GP)16 with a deep kernel modelled by a deep neural network, which has both advantages of deep neural network and GP. We adopt the deep kernel learning to replace the original deep neural network, which could encode more uncertainty. For example, the prediction of action-value function from this algorithm is not just the action but also the variance of such action. Further, a new weighted sampling strategy is developed. The prediction variance from deep kernel learning is used as the weight for each historical interaction, and then the model is updated using the samples from weighted interactions. The experimental evaluation on standard RL testing platform -OpenAI.Gym-* has demonstrated that the new algorithm could reach larger scores. In summary, the main two contributions of this article are as follows:
- •
we propose a new model-free RL algorithm based on deep kernel learning with better performance comparing the classical deep neural network-based one;
- •
a new weighted sampling strategy is developed to fully take advantage of the replay memory to further improve the algorithm performance.
The remainder of this article is organised as follows. Section 2 discuses related work. The new model-free RL algorithm is introduced in Section 3. Section 4 evaluates the proposed RL algorithm on standard RL testing platform through comparing the classical algorithm. Section 5 concludes this study and discusses possible future work.
2. Related Work
In this section, we briefly review the related work of this study. The first part summarizes the literature on model-free reinforcement learning and the second part summarizes the literatures on Bayesian deep models.
2.1. Model-free RL
Model-free RL aims to learn an optimal policy for an agent without explicitly modelling the environment. Existing works in this direction can be mainly grouped into three categories: value-based, policy-based, and combined22. Policy-based RL is to directly optimise the parameters of the policy aiming to maximise the expected reward, and policy gradient is a typical algorithm of this category. Value-based RL is to learn the action-value function first aiming to minimise the temporal difference error and then design the policy based on this function. According to the difference on the computation of temporal difference error, there are two kinds in value-based RL: on-policy one which computes the temporal difference error based on current policy, e.g., SARSA; off-policy one which computes the temporal difference error based on greedy policy, e.g., Q-learning. Deep Q-Networks (DQN)13 is a seminal work of Q-learning, which adopts deep neural network to approximate the Q-function. Such algorithm is proofed successful on Atari games and even exceeds the human performance. Based on DQN, Double-DQN24 is proposed to separately model action-selection and Q-function by two deep neural networks, which resolves the possible overestimate problem in DQN. The performance can be further improved by splitting Q-function into state function and advantage function in Dueling DQN26. There are also works that try to combine two categories, e.g., Deep Deterministic Policy Gradient10. This paper will only target on DQN and replace the traditional deep neural network with Bayesian deep models, and other advanced extensions can also be easily adopted later.
2.2. Bayesian deep model
The Bayesian paradigm for machine learning, also known as Bayesian (machine) learning, is to apply probability theories and techniques to represent and learn knowledge from data. Some renowned examples are Bayesian network, Gaussian mixture models, hidden Markov model15, Markov random field, conditional random field, and latent Dirichlet allocation1. Compared to other learning paradigms, Bayesian learning has distinctive advantages: 1) representing, manipulating, and mitigating uncertainty based on a solid theoretical foundation - probability; 2) encoding the prior knowledge about a problem; 3) good interpretability thanks to its clear and meaningful probabilistic structure. Inspired by the recent success of deep learning, researchers start to pay attention to build Bayesian deep models25 aiming to combine the advantages from two areas. One straightforward strategy is to assign probabilistic prior for parameters of traditional deep neural networks, e.g., Gaussian prior 6,4. Such Bayesian method could avoid some of the pitfalls of stochastic optimisation. Bayes by Backprop2 -a variational inference method- is proposed to efficiently resolve these models. Another strategy is to pave the probabilistic models deeply. Deep belief networks 8 may be the earliest one, which has undirected connections between its top two layers (it is actually a RBM7) and downward directed connections between all its lower layers. Its advantage is that it needs less time to train the model, but there is no feedback from top to bottom. On the contrary, Deep Bolzman Machine (DBM)18, which is the multi-layered RBM, requires more time for model training but there is feedback from top to bottom so it is more robust. The hidden units in DBN and DBM are restricted to be binary. To resolve this constraint, Gamma belief networks29 and deep poisson factor analysis5 are proposed using Gamma and Negative-binomial distributions, which could build deep structure with nonnegative real hidden units. Deep latent Gaussian model17 is another deep Bayesian model built by Gaussian distributions. Beyond Gaussian distributions, Gaussian process (GP) is also adopted for constructing Bayesian deep models. For example, deep neural network is used to construct a deep kernel as the covariance function of GP in deep kernel learning28,27; the other idea is to pave more Gaussian process on each other known as deep Gaussian process3.
3. The Proposed Model
RL is often modelled by a Markov decision process as†< S,A,P,R,γ >, where S is a set of environment states, A is a set of agent actions, P defines the state transition of environment, R defines the reward from environment, and γ is the discount factor. The goal of RL is the agent policy π(s) which is a mapping from environment states to actions aiming to maximise the (discounted) expected long-term reward
3.1. Preliminary: Deep Q-Network
Q learning12 is a methodology to resolve RL by evaluating the value Q(s,a) of action a given state s which is also known as Q-function. Such value could be considered as the expected “reward” from taking this action under this state. To learn this action-value function (a.k.a., Q-function), an effective method is temporal difference learning21 which minimises the difference between current value of an action and its optimal value according to the next step
3.2. Bayesian deep RL
We propose a Bayesian Deep RL (DBRL) to adopt Gaussian process with deep kernel28 to model Q(s,a). A Gaussian Process (GP)16 is defined as a collection of random variables, any finite number of which have (consistent) joint Gaussian distributions
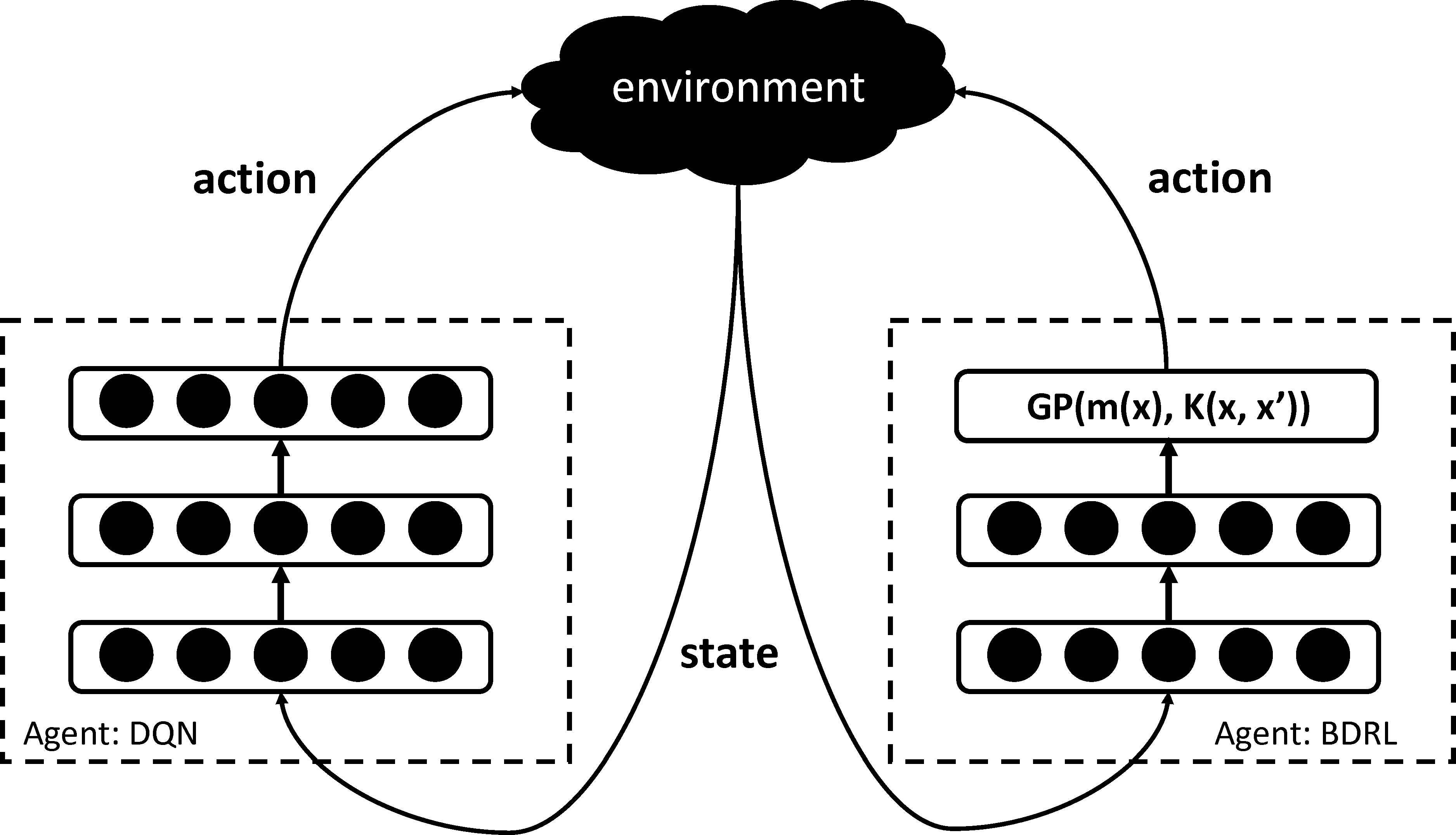
Interaction between an environment and two agents: DQN and BDRL
Experience replay is another genius in DQN, where historical interactions are saved in memory for Q-function learning. The original memory structure is
We add the action uncertainty (i.e., prediction standard deviation) from GP as another column to the memory,
Rather than uniform sampling, weighted sampling is adopted when the historical interactions are retrieved for model training, where each interaction is weighted by

Bayesian deep RL
4. Experiments
We evaluate BDRL on a open RL testing platform: OpenAI.gym and compare it with DQN in this section.
4.1. Setting
In the following, we choose the simple environment ‘CartPole-v1’‡in OpenAI.gym. This environment has two actions (i.e., move left or right), its state is a four dimensional vector, and a reward of +1 is provided for every timestep that the pole remains upright. One episode ends when the pole is more than 15 degrees from vertical or the cart moves more than 2.4 units from the center. At first, we take 10,000 steps to explore the state space and construct the initial experience memory, where the action is randomly chosen not from RL algorithms. After the exploring, we take 15,000 steps to train the RL algorithms using ε-greedy strategy with a decreasing ε value and minimum value 0.01. Finally, we test 10,000 steps only using RL algorithms and record the total reward as score for each episode. The higher score means better RL algorithm. The memory size is set as 10,000 and the batch size is 32. Every 150 steps, the fixed target Q-function is updated by the latest evaluation Q-function. The other two hyper-parameters are γ = 0.99 and learning rate 0.00025 for the optimisor. For DQN, we build a deep neural network that contains two hidden fully connected linear layers with 512 and 128 nodes and activation function is ReLU. For BDRL, we use a deep neural network containing two hidden (linear) layers with 10 nodes in each layer and activation function is tanh, and RBF kernel is used for GP. The implementation of BDRL is based on DKL§.
4.2. Results
At first, we compare the performance of DQN and BDRL under same setting where both of them use uniform sampling when retrieving replay memory for deep model update. The result is shown in Fig. 2, where the scores of all episodes in testing stage are plotted. According to this figure, we can observe that: 1) BDRL can reach much higher score than DQN. The highest score from BDRL is 346, which means the car makes 346 moves with the bar upright. 2) The average score of BDRL (113.52) is also better than the one of DQN (98.33). 3) The episode number of BDRL (88) is smaller than the one of DQN (102) within the same number of steps (i.e., 10,000). 4) Although the overall results of BDRL is better than DQN, the line for BDRL is with stronger fluctuation than the one for DQN, which means the results from BDRL is unstable comparing with the ones from DQN.
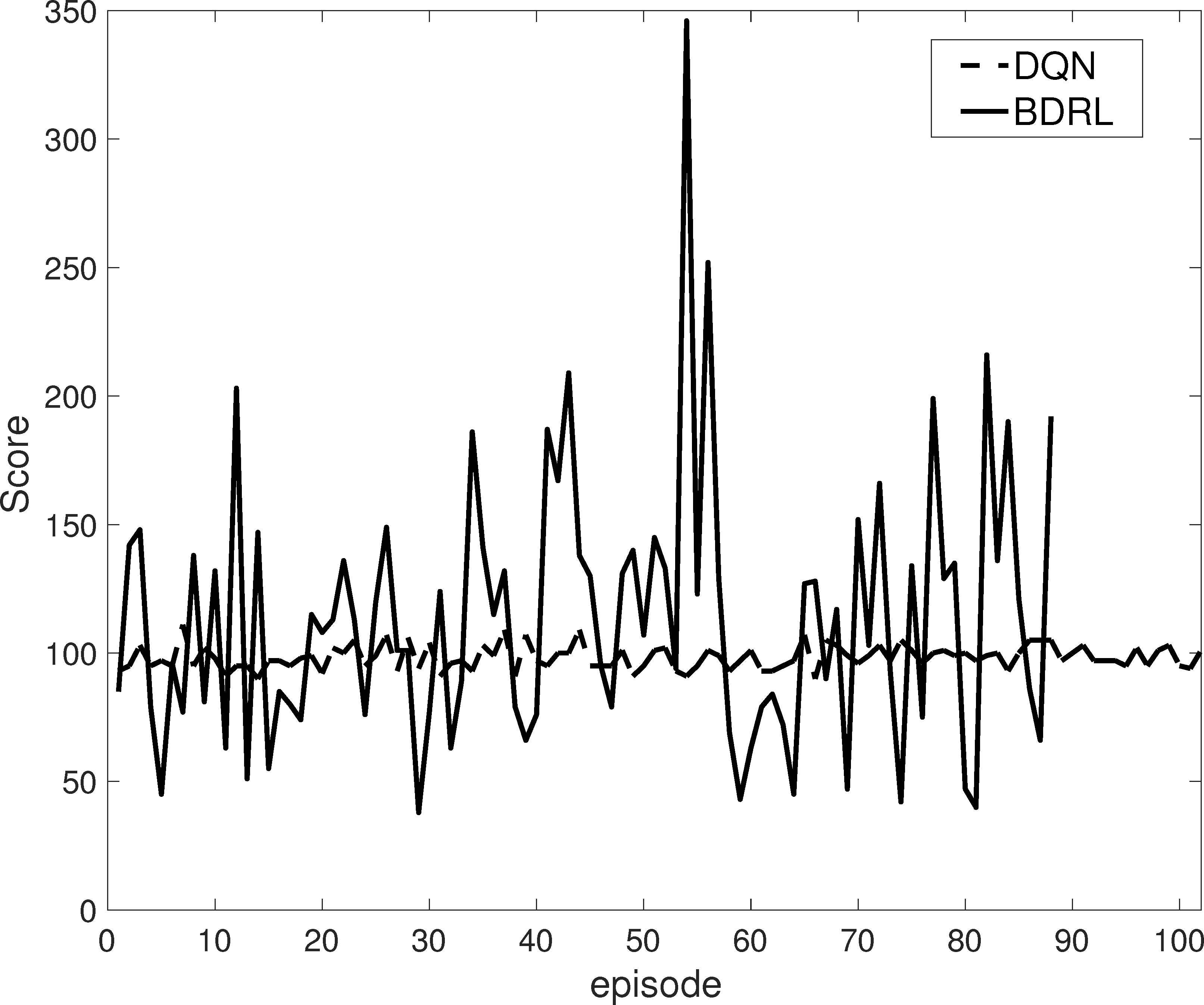
Evaluation of the efficiency of BDRL through comparing with DQN on ‘CartPole-v1’. The scores (the higher is the better) of all episodes in testing stage from both algorithms are plotted. The average scores from BDRL and DQN are 113.52 and 98.33, respectively.
Then, we evaluate the proposed weighted sampling strategy for replay memory. We run BDRL using two different sampling strategy: uniform and weighted (according to Eq. (6) with α = 0.1. Note that during the exploring stage, the action is randomly chosen and their weights are also randomly assigned. The result is shown in Fig. 3, where the scores of all episodes in testing stage are plotted. According to this figure, we can observe that: 1) The episode number of BDRL with weighted (73) is smaller than the one of BDRL with uniform (88) within the same number of steps (i.e., 10,000). 2) The average score of BDRL with weighted (136.75) is also better than the one of BDRL with uniform (113.52). Therefore, we can draw the conclusion that the proposed uncertainty-based weighted sampling strategy could better take advantage of replay memory and improve the efficiency of the BDRL.
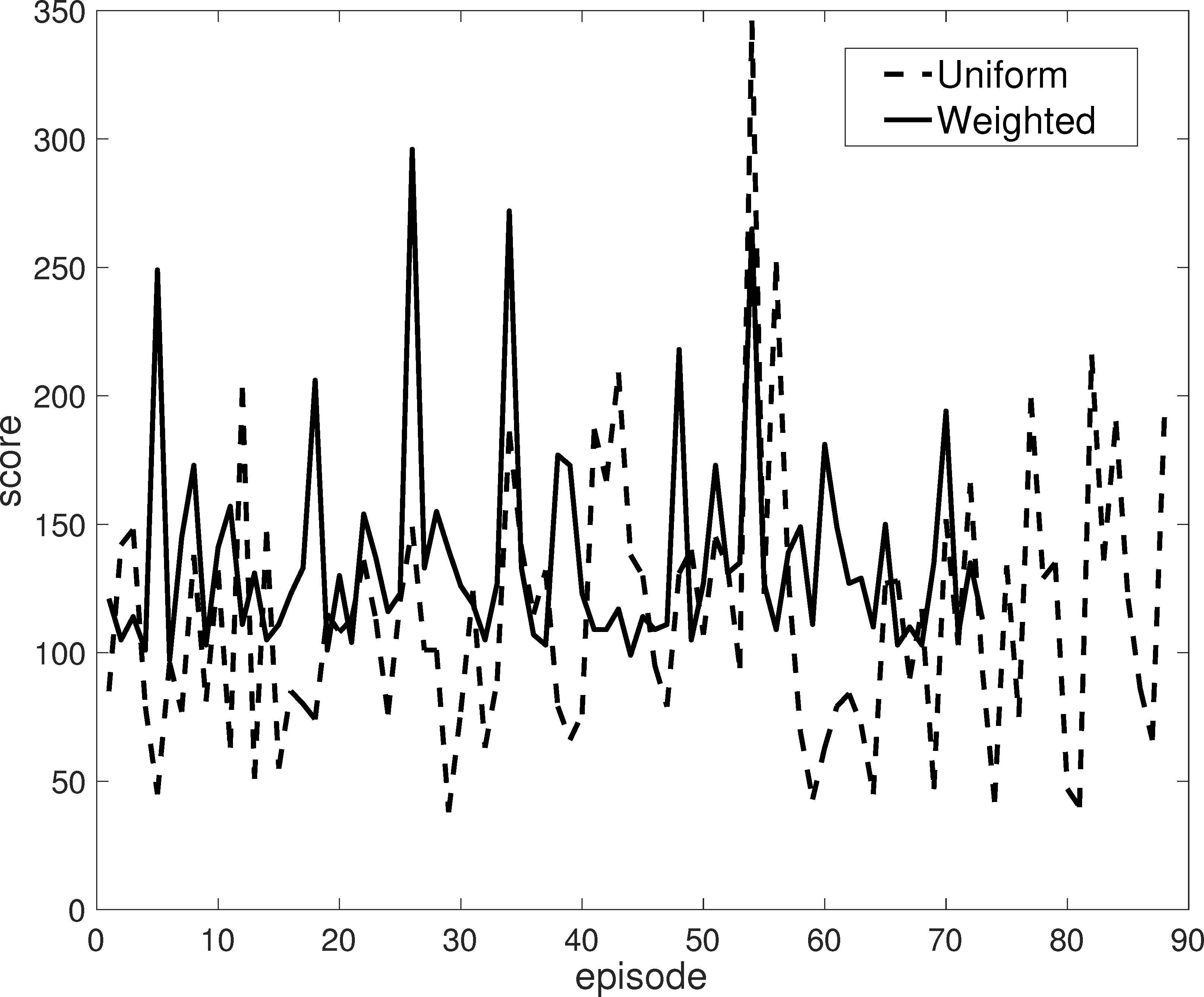
Evaluation of the efficiency of uncertainty-based weighted sampling strategy for replay memory on ‘CartPole-v1’. The scores (the higher is the better) of all episodes in testing stage from BDRL with uniform and weighted strategies are plotted. The average scores from BDRL with weighted and BDRL with uniform are 136.75 and 113.52, respectively.
5. Conclusions and Further Study
In this study, we have presented a new model-free reinforcement learning (RL) algorithm based on Bayesian deep model. This Bayesian deep RL (BDRL) algorithm has unique advantages compared with deep Q-network (DQN) that is the deep neural network (DNN)-based RL algorithm, i.e., more ability to handle uncertainty and take advantage of past experience. The experiments on standard reinforcement learning testing platform demonstrated its effectiveness on RL tasks, and the comparison with DQN showed the superior performance of the proposed algorithm than the DNN-based one. In this paper, we only use on one simple task to demonstrate the effectiveness of the proposed ideas, and we will test them using more and harder tasks in the future. We believe that this study is only a start point, and there are many interesting following works. One interesting direction for further study would be to add more Gaussian process layers to the deep architecture based on deep Gaussian process3; the second interesting direction is to build new Bayesian nonparametric deep models23 for more flexible Q-function learning with less tunable parameters; the third one is to incorporate the temporal difference error19 and marginal likelihood from GP into the weights for interactions in replay memory; and the last one is to apply fuzzy systems techniques to the Q-learning process to deal with decision processes13 in which the goals and constraints are fuzzy in nature. These future investigations are expected to provide backbones for applying RL techniques to support dynamic decision-making in complex situations that involve massive data domains, agents, and environments.
Acknowledgments
This work is supported by the Australian Research Council (ARC) under Discovery Grant DP170101632.
Footnotes
References
Cite this article
TY - JOUR AU - Junyu Xuan AU - Jie Lu AU - Zheng Yan AU - Guangquan Zhang PY - 2018 DA - 2018/11/01 TI - Bayesian Deep Reinforcement Learning via Deep Kernel Learning JO - International Journal of Computational Intelligence Systems SP - 164 EP - 171 VL - 12 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.2018.25905189 DO - 10.2991/ijcis.2018.25905189 ID - Xuan2018 ER -
