Spontaneous Concept Learning with Deep Autoencoder
- DOI
- 10.2991/ijcis.2018.25905178How to use a DOI?
- Keywords
- artificial intelligence; machine learning; deep learning; unsupervised learning
- Abstract
In this study we investigate information processing in deep neural network models. We demonstrate that unsupervised training of autoencoder models of certain class can result in emergence of compact and structured internal representation of the input data space that can be correlated with higher level categories. We propose and demonstrate practical possibility to detect and measure this emergent information structure by applying unsupervised clustering in the activation space of the focal hidden layer of the model. Based on our findings we propose a new approach to training neural network models based on emergent in unsupervised training information landscape, that is iterative, driven by the environment, requires minimal supervision and with intriguing similarities to learning of biologic systems. We demonstrate its viability with originally developed method of spontaneous concept learning that yields good classification results while learning new higher level concepts with very small amounts of supervised training data.
- Copyright
- © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Over recent years, the domain of biology-motivated machine learning has seen very fast, one can even say exploding growth. A number of breakthrough advances have been made, bringing efficiency and confidence in training of machine learning systems and specifically, deep neural networks, in several areas of application such as image recognition, time series analysis, games and others to that of human abilities or even surpassing them.
Citing only a few of many advances in data processing, activation, optimization, and other stages of designing and training of deep neural networks with very large data sets and ranges of classification categories, Kingma and Ba [1] developed advanced stochastic optimization training with adaptive learning rate that allowed to improve both accuracy and training time of deep neural networks. He, Zhang et al. [2] introduced parametric rectified linear unit activation (PReLU) with significantly improved accuracy, leading to human-level accuracy in image recognition. Introduction of residual learning and stochastic learning approaches allowed to train networks with virtually unlimited depth. He, Zhang et al. [3] achieved success in training deep neural networks of up to a thousand layers with significantly improved accuracy in image recognition. Stochastic depth training algorithms developed by Huang, Sun et al. [4] now allow to train deep neural networks with over 1200 layers, while significantly reducing training time and achieving outstanding accuracy in image classification.
Many other significant advances have been made in all stages of deep learning from data processing to optimization, regularization and training algorithms and methods leading to deeper and more complex networks that can train in shorter times with massive datasets while achieving superior accuracy in classification of complex real world data in a wide and rapidly growing range of applications in multiple domains.
1.1. Related Work
In an exciting breakthrough in self learning with training method based entirely on self-play reinforced learning with no human supervision, DeepMind team developed AlphaGo Zero Go game player system that achieved superior performance among both machine players and humans, defeating previous world champion defeating version with a score 100-0 while learning entirely on its own through self-play with no supervised training (refer to Silver, Shrittwieser et al., [5] on reinforced self-play learning). Iterative, progressive and self-reinforcing unsupervised learning can prove an important step toward general learning directly from the environment with minimal external supervision.
Interesting results in unsupervised training with deep autoencoder neural networks were reported by Le, Ranzato et al., [6]. Training an experimental deep neural network in unsupervised mode with a very large array of images they observed emergence of concept sensitive neurons – those activated by images of certain abstract category such as a human or animal face. While accuracy of recognition reported in the study, being in the fractions of a percent, was not yet at a confident level, these results open new possibilities in studying spontaneous emergence of concept associated structures in the information landscape of deep neural networks.
Tishby et al. in [7] offered profound insights into possible basic principles of information processing in deep learning systems. In the “bottleneck” argument proposed by the authors, generalized concepts emerge as a result of “squeezing” or statistical grinding of information through the layers of the deep learning model, filtering out irrelevant details while preserving essential higher level structures in the input data that set the foundation of generalizing ability of these systems. We shall discuss how it can be related to results of this study in more detail in the discussion section.
An in-depth review of essential up-to-date developments in biology-motivated machine learning with applications of advances and findings in neuroscience to machine intelligence can be found in Hassabis, Kumaran et al. [8], notably in application to general learning and spontaneous learning, continual learning models (Cicon-Gan, Hayashi-Takagi and others), probabilistic and deep generative learning models (Lake et al., Rezende et al.), progressive learning and conceptual representation, while essential concepts, results, promises and challenges in application of deep neural networks in artificial intelligence were investigated ain great scope and detail by Y. Bengio [9].
While impressive progress has been made in training and adapting AI systems and specifically, deep learning neural networks to very wide and growing by day array of tasks and applications often with outstanding success, one cannot help pointing out some areas where advances have been slower. First, the achieved success is often limited to a specific application, skill or problem area, with limited capacity for more general and environment motivated self-learning.
Secondly, the process of training machine intelligence systems with fixed categories and massive amounts of truth data may not always be efficient or practical in a dynamic and fluent information environment, where emergence of new concepts and/or obsolescence of others would require frequent retraining of the learning system; nor is it reminiscent of learning processes of biologic systems. As pointed out by Hassabis et al., “human cognition is distinguished by its capacity to rapidly learn about new concepts from only a handful of examples” that is, it tends to be iterative, adaptive to the environment and based on trials and errors with limited ground truth data, while achieving gradually over the training phase high levels of confidence in recognition of newly learned concepts, including those encountered spontaneously without any previous training.
The motivation for this study is to approach both of these challenges from the direction suggested by Le et al. and earlier studies that is, by exploring possible link between unsupervised training of certain deep neural network models and emergence of concept sensitive structures in their inner layers. Should such a link be established, that is the first question explored in this study, could it be used as foundation for a novel approaches to training of machine intelligence systems that is based on the emergent unsupervised information landscape, requires minimal supervision and other substantial improvements to traditional training methods?
1.2. Original Contribution
We examine effective transformation of data during unsupervised training with autoencoder model of specific design that allows detailed evaluation and measurement of structure and composition of information in its hidden layers, and demonstrate the emergence of a compact and structured representation of input data that can be correlated with higher level categories. An original approach developed in the study is to apply unsupervised proximity clustering in the activation space of the central hidden layer (that we refer to as “encoded space”) that allows to observe and measure structures and features in the encoded space in completely unsupervised mode without any ground truth data. In a number of experiments we provide several strong arguments that the emergent in unsupervised training structure can be associated with higher level categories in the input data.
Based on these findings, we point to possibility of using this spontaneously emergent structure in a new class of training methods that could be iterative, driven by the environment with smaller amounts of supervised training data compared to traditional approaches (information landscape based learning). We illustrate this possibility by developing a landscape based training method and apply it to real world data demonstrating good learning progress and classification performance with minimal supervised training.
In conclusion, we discuss theoretical principles and foundations of unsupervised concept learning and present a hypothesis on information processes that lead to emergence of structure in the inner information space of deep autoencoder models.
2. The Main Text
The structure of the paper is as follows: in the following Section 3 we describe the model, data and methods used in the study. Section 4 contains the results by category of analysis, including Spontaneous Concept Learning method developed in the study (Section 4.4). Finally, Section 5 contains discussion of the results, possible applications, and further directions of research.
3. Instruments and Methods
The model in this study contains several essential components with a deep autoencoder neural network in its core. Autoencoder neural networks that were studied extensively in applications to unsupervised learning were chosen in the study for several reasons: they can train in unsupervised mode without any ground truth data; earlier studies indicated possibility of spontaneous concept sensitivity in certain autoencoder based models; they have certain parallels to biologic systems in which reproduction of the outside environment is a common task of survival; finally, advances in design and optimization of neural networks allow for efficient training and execution of experiments.
The model data and methods used in the study are described in detail in the following sections.
3.1. Model
The model is a deep autoencoder neural network with three main hidden layers and several advance activation and normalization layers in near-symmetrical layout as illustrated in Fig.1 and further defined in Table 1 below.
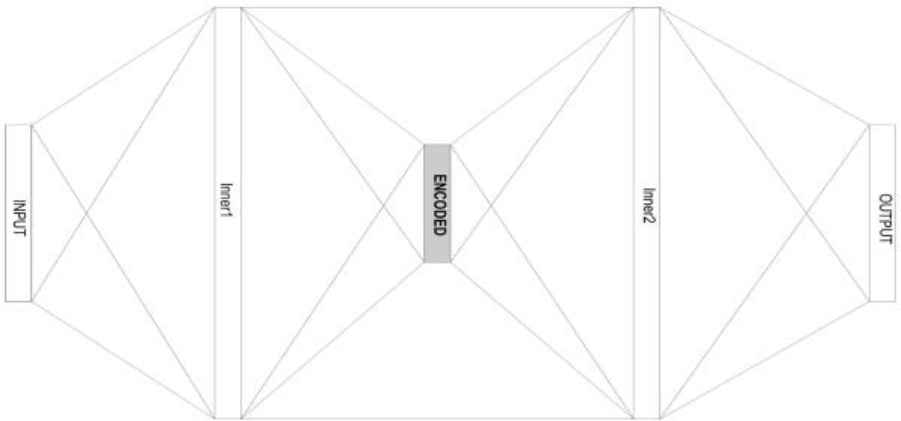
dAEN model layout
| Layer | Size | Range | Activation | Shape | Loss |
|---|---|---|---|---|---|
| Input | F=22 | [0..1] | (,F) | ||
| Inner1, 2 | M=10..100 | Any | Leaky Relu [11] | (,M) | |
| Encoded | N=3..10 | Any | Leaky Relu | (,N) | |
| Out | O = F = 22 | [0..1] | Sigmoid | (,F) | MSE |
Model Parameters
We use this particular design (nicknamed as “dAEN”), with inflated first and last hidden layers and strongly compressed central layer because based on results of measurements (Section 4.1.1) it appears to produce more compact and structured representation of input data space in the central layer of the model. For complete graph of the model refer to the Appendix.
Depending on the size of hidden layers, dAEN models in the study had up to 8,000 parameters as described in Table 1. Models were implemented in Python with Keras [10] and Tensorflow.
Hereinafter, “M-N dAEN model”, e. g. “dAEN 50-5” will refer to a model with sizes of hidden layers M, N, M, respectively, in the order from input to output.
3.2. Components
Along with autoencoder model described above, the learning system uses a number of other components that are described in this section.
The autoencoder model is trained in unsupervised mode to match the output to the input with Mean Squared Error loss function.
Trained model performs “encoding transformation” from the input data space X to its representation in the Encoded layer of the model y as:
To classify input samples to higher level categories {C}, a classifier method is trained with ground truth labeled set (X, L) in encoded space of the model:
Together, the encoder and classifier can predict the class C of an input sample S by transforming it to the encoded space E, then predicting C with classifier trained on E. In our model, we use geometry based classifier such as k-nearest neighbor.
In the unsupervised training phase one can apply proximity based clustering method that doesn’t require fitting with labeled samples, such as MeanShift [12]. It can be fitted on a subset of data in the encoded space of the model to learn and visualize its structure as:
Classes C and Cl thus signify the distinction between the known higher level category of the sample in supervised training, “the external knowledge”, and its internal concept (“implicit knowledge”) derived in unsupervised training of the model and clustering in its encoded space. By combining unsupervised clustering with deep autoencoder model we’re able to detect and identify the structure of information that emerges in the hidden layers of the model during training in entirely unsupervised mode, before any ground truth samples have been applied.
The complete learning system can then be defined as a combination of: 1) dAEN autoencoder model with encoder sub-model; 2) concept classifier (or a set thereof) and 3) unsupervised structurer that maps the encoded space E to a set of clusters identified in unsupervised fitting.
3.3. Data
To reduce possibility of data specific effects we use two different and independent data sets. The data represents Internet sessions recorded in two different networks by geographic location and source. Each sample represents an instance of Internet session such as a voice call, web browsing session, instant messaging session, file download, etc. Samples are defined by 22 parameters derived from basic statistics of data packets.
| Type | Q-ty | Description |
|---|---|---|
| General | 6 | Total duration, total data size (per direction), number of packets (per direction), data protocol |
| Packet size | 8 | Min, Max, Mean, Standard deviation of data packet length, per direction |
| Packet timing | 8 | Min, Max, Mean, Standard deviation of data packet inter arrival time, per direction |
Input Data
We use two different, independently obtained and processed datasets. The first dataset A consists of approximately 50,000 samples recorded in NIMS lab of Dalhousie University [13]. These samples are labeled with three categories and arranged into two different non-overlapping sets: A-Train (41,600 samples) used in unsupervised training and A-Test (10,000 samples) used in accuracy testing. The sets are kept separate with no overlapping to ensure that test metrics are measured with samples that the model has not seen in unsupervised training.
| Category | Samples | Representative | Label |
|---|---|---|---|
| Voice | 20,000 | GTalk, VoIP | “0” |
| Web | 12,000 | HTTP, Web browsing | “1” |
| Other | 20,000 | Instant messaging, file transfer and other | “2” |
Dataset A, Composition
The second dataset B is produced from live recording of Internet data in New Zealand (Waikato Internet Traffic Storage, [14]) and is comprised of approximately 240,000 unlabeled samples with the same input parameters as Set A. This data, being a live recording in a core Internet network has much wider representation of patterns, with over 4,000 distinct applications (for comparison, ImageNet has approximately 20,000 categories of images). To evaluate classification accuracy a subset of the dataset has been labeled for several common Internet applications by well-known port number.
3.4. Training and Classification
The model is trained with unlabeled data to achieve reproduction of input samples in the exit layer of the network. The performance of unsupervised training is measured by validation accuracy and loss. In the study, models achieved the following training results:
Dataset A: validation accuracy 88 – 94%, validation loss 0.0015 – 0.004
Dataset B: validation accuracy 95 – 97%, validation loss 0.00025 – 0.001
Classification accuracy can be measured with labeled data by obtaining prediction as in Eq. (4) that can be compared with ground truth. We use accuracy metrics as commonly defined: classification accuracy or recall as True Positive samples (class) / Total samples (class); and false positive rate as False Positive (class) / Total samples (not in class). We also use total accuracy measure for all classes defined as Total True Positive (all classes) / Total Number of samples.
It’s worth noting that a priori, there’s no expectation of correlation between accuracy in unsupervised training vs. classification accuracy with labeled data. For clarity they are referred to as “training accuracy” vs. “classification accuracy” in the rest of the study.
3.5. Measurement and Visualization
Measurement and visualization is performed with a sampling subset that is transformed to encoded space (Eq. (2)) and visualized by plotting the encoded sample in the dimensions of encoded space. We use random sampling with 2 – 10% of the dataset.
The size of the sample in the encoded dimension is measured as (max Xn – min Xn), where Xn is the coordinate of the sample in that dimension. Note that identifying and measuring cluster structure thus requires no supervised data.
All results were measured over multiple runs to eliminate possibility of statistical fluctuation. Classification accuracy results with labeled dataset were 20 – 100 fold cross validated. Results related to training of models, such as shape and structure, classification accuracy in training and concept learning were measured over minimum 10 training runs.
3.6. Spontaneous Learning
Based on results pointing to correlation of the emergent information structure in the encoded space with higher level categories we attempted to illustrate possibility of using this structure in training the system to learn and recognize new higher level categories.
The method is based on developing a set of “concept markers” in the encoded space over a series of learning iterations that aim to identify clusters and structures relevant to higher level category being learned. Concept markers are built with small number of truth samples in trial and error iterations and artificial or “synthetic” markers derived from structures identified with clustering following unsupervised training. In each learning iteration, the set of concept markers is updated based on real world inputs and classifier is retrained with the updated set of markers iteratively improving prediction performance.
4. Results
In this section results are presented by type of analysis. We report evaluation and measurement of the emergent structure in the encoded space, compare it with other unsupervised ML methods, evaluate training and classification performance of models and correlation of emergent unsupervised structure with higher level categories in the input data. In Section 3.4 results are presented for spontaneous concept learning method developed in the study.
4.1. Shape and Structure
We observe that unsupervised training of dAEN model results in compact and structured representation of input data space.
4.1.1. Shape and Structure in Encoded Space
In Table 4, characteristics of the encoded space of 50-5 and 50-3 dAEN models were measured after 100 epochs of unsupervised training. For each run the number of visible features in visualization sample is recorded along with number of clusters calculated by structuring method (MS), as well as minimum and maximum size of the sample.
| Model | Train. Loss | Train. Acc. | MS clusters | Visible clusters | Size |
|---|---|---|---|---|---|
| Set B | |||||
| 50-5 | 6 × 10−4 | 96.8% | 17 | 16 | 0.015 / 0.022 |
| 50-3 | 9 × 10−4 | 96.2% | 16 | 14 | 0.019 / 0.032 |
| 25-3 | 0.0011 | 96.2% | 13 | 10 | 0.019 / 0.034 |
| Set A | |||||
| 50-5 | 0.001 | 88% | 13 | 15 | 0.018 / 0.054 |
| 50-3 | 0.0022 | 93.4% | 12 | 15 | 0.018 / 0.04 |
Characteristics of Encoded Space
In visual observation of the encoded sample one can identify multiple structures such as clusters, streaks, and other distinct regions in encoded space. Clusters identified by proximity clustering method mostly agree with visual observation. In Fig.2, visualization sample from Dataset B is plotted in the encoded space of 50-3 dAEN model with identified clusters. For illustration, samples of one application (Messenger), are shown in magenta.
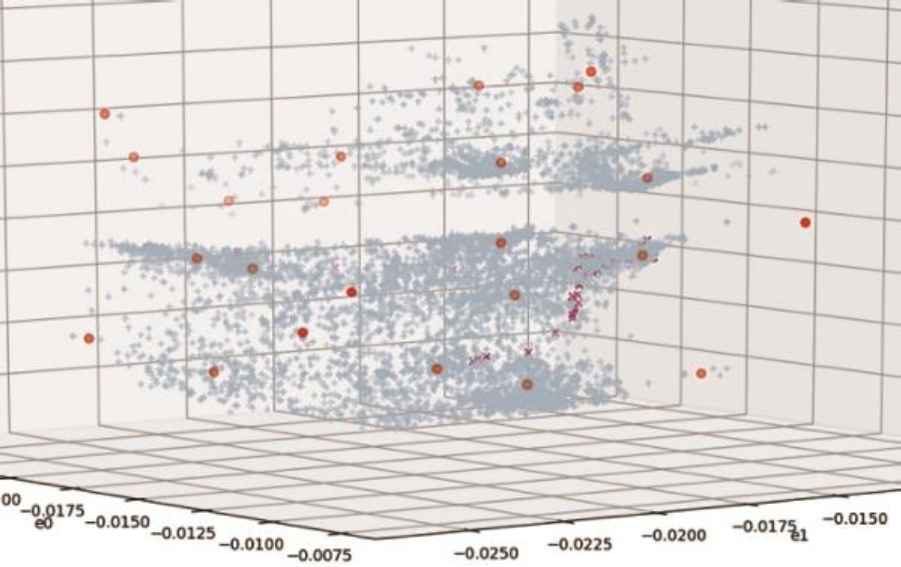
Encoded space with MS clusters
One can compare structure produced by unsupervised training of dAEN models with transformations by other unsupervised machine learning methods. Of those, most commonly used are PCA and unsupervised clustering such as K-Means. As unsupervised K-Means requires as essential parameter the number of expected clusters that wouldn’t be known a priori in unlabeled real world data, we see it as less applicable in this analysis.
By applying PCA decomposition to the same number of dimensions as encoded space of dAEN model on the same visualization sample one can compare the results of transformation by dAEN model vs. PCA.
It can be seen that the resulting PCA transformation space is quite different from that of dAEN models, with more uniform distribution of samples and fewer distinct features. Unsupervised clustering detects fewer features in PCA transformed sample as well. It can also be seen that the size of the sample in the PCA space is by orders of magnitude greater than in the dAEN space.
| PCA | MS clusters | Visible clusters | Size (Min / Max) |
|---|---|---|---|
| Set B | 12 | 10 | 1.85 / 2.2 |
| Set A | 10 | 12 | 1.75 / 2.0 |
Characteristics of PCA Space
Another way to compare data transformations by dAEN models and PCA is to examine projections of the visualization sample in the two dominant dimensions. In Fig.3 the same sample from dataset A is transformed by dAEN 50-3 model (top) and PCA 3-dimension decomposition, bottom.
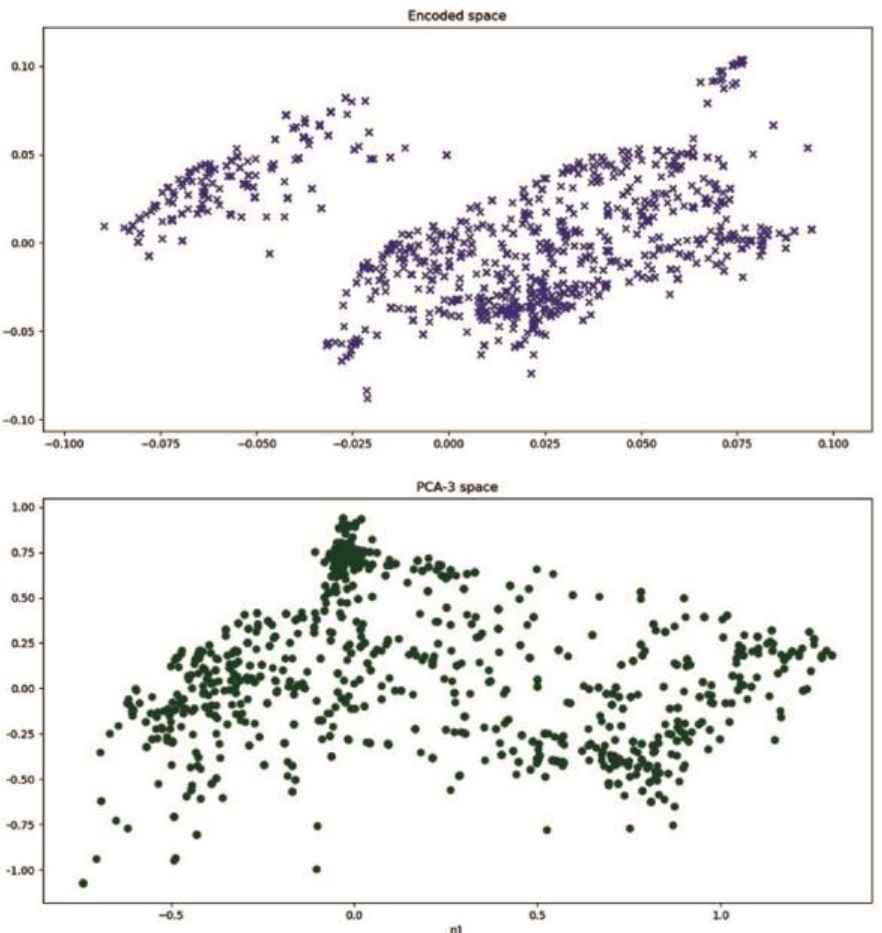
Structure in dAEN vs PCA space
It is our intent to extend structure analysis performed in this section to more complex neural network models in the future studies. This would require considerable insight and effort in constructing the effective encoded data space from large number of intermediate layers, including those with sparse activations commonly used in such models.
4.1.2. Shape and Structure in Training
It is possible to monitor changes in the shape and structure of the sample in encoded space as the model trains in unsupervised mode by applying Keras callback. A simple callback measured and visualized data sample after each n-th epoch of unsupervised training.
In this training run of a 50-3 model over 100 training epochs (dataset A), we record the size of visualization sample in dimensions of the encoded space and the number of visibly identifiable features in the sample as training progresses:
| Epoch | Visible clusters | Sample Size |
|---|---|---|
| 0 | 5 | 0.975, 0.560, 0.478 |
| 20 | 8 | 0.027, 0.063, 0.031 |
| 40 | 10 | 0.024, 0.044, 0.024 |
| 60 | 12 | 0.024, 0.042, 0.024 |
| 80 | 12 | 0.024, 0.044, 0.024 |
| 100 | 13 | 0.0235, 0.042, 0.024 |
Size and Structure in Training
It can be seen that as the sample is compressed to less than 10-4 of its initial size, the number of identifiable features increases more than twofold.
In all training runs with both data sets, we have observed significant reduction in the volume of the measuring sample in the course of training, the effect not seen in other unsupervised ML methods such as PCA. These results demonstrate that compression and structuring effect of unsupervised training of dAEN models and possibly, other autoencoder based neural network models is a distinct feature of these models. Further in the study we will refer to it as “unsupervised spontaneous structuring”.
4.2. Classification
In the previous section we have observed that unsupervised training of dAEN models produces compact and structured encoded space, however there was no indication of if or how it is correlated with higher level categories in the input data. Classification experiments presented in this section indicate that such correlation may indeed exist.
In classification experiments we used labeled dataset and training process as described in Sections 2.2 and 2.3.
4.2.1. Classification Accuracy
In this table classification accuracy results are summarized for dAEN 50-5 model. As accuracy results strongly depend on the size of supervised dataset used in training of the classifier, several points were measured, from 500 (1% of unsupervised training dataset) to 100 samples (∼ 0.2%).
For comparison, as in Section 4.1.1, classification accuracy was also measured with classifier trained with the same training sample transformed by PCA decomposition to the same number of dimensions as dAEN model (Table 7, last rows).
| Label Samples | Accuracy % | FPR, % | Total Acc., % | STD, Accuracy |
|---|---|---|---|---|
| 500 | 99.2 | 0.9 | 98.6 | 0.00011 |
| 300 | 98.7 | 3.7 | 96.5 | 0.00018 |
| 100 | 98.1 | 5.2 | 95.7 | 0.00023 |
| PCA, 300 | 98.5 | 4.4 | 96.2 | 0.00021 |
| PCA, 100 | 97.8 | 5.0 | 94.8 | 0.00024 |
Classification Accuracy
While on average dAEN models do not significantly outperform PCA based ones, we observed that some models achieve outstanding performance when trained with very small amounts of training data. For example, these 50-5 models demonstrate accuracy results below given that they were trained with only 30 labeled samples i.e. ∼ 0.06% of unsupervised training dataset (the accuracy metrics are, respectively: default category accuracy, default category FPR and total accuracy across all categories):
| dAEN-1-32: | 0.97392502, 0.09018429, 0.85562 |
| dAEN-2-32: | 0.9547335, 0.06949415, 0.87671 |
In the experiments where very small amounts of training data were used, dAEN models trained in unsupervised mode outperformed all common ML methods in classification accuracy, including decision trees, MLP, kNN, SVM and PCA.
In our view, this can be first indirect indication that unsupervised spontaneous structure observed in the previous section can be positively correlated with higher level categories in the input data. Indeed, if no such correlation existed, training dAEN models with any set of ground truth data should not have resulted in statistically significant improvement compared to classification on PCA reduced space. But if such correlation indeed exists, the pattern of accuracy results would be exactly as observed, with smaller comparative accuracy gain on a larger training set smoothing granularity of the spontaneous unsupervised structure, while a “right” training sample in the structured space (that is, with good representation of training samples in the structures relevant to the category being learned) could produce very good classification accuracy even with extremely small training set.
4.2.2. Classification Accuracy in Training
As in Section 4.1.2 above, one can monitor classification accuracy in training with a callback. A callback receives verification sample on which accuracy test is performed after each n-th epoch of unsupervised training. In this example of 50-5 model, total classification accuracy across all classes improved from 86.5% to 91.2%, i.e. by approximately 5% (here, “lr” is learning rate, “accuracy” being total classification accuracy for all classes):
| epoch: 0 | lr: 1.0 | accuracy: 0.8652 |
| epoch: 20 | lr: 0.5 | accuracy: 0.9084 |
| epoch: 40 | lr: 0.125 | accuracy: 0.91 |
| epoch: 60 | lr: 0.0078 | accuracy: 0.9136 |
| epoch: 80 | lr: 0.001 | accuracy: 0.9124 |
| epoch: 100 | lr: 0.001 | accuracy: 0.9124 |
In all conducted experiments classification accuracy increased as a result of unsupervised training in all cases, with the mean of 4.6% and the range 2.8 – 7.7%. In our view this result can be another indication that emergent structure in the encoded space is correlated with higher level categories in the input data. If the emergent spontaneous unsupervised structure had no significant correlation with higher level categories, positive correlation between unsupervised training and the improvement in classification accuracy would be difficult to explain.
4.3. Categorization in Encoded Space
Categorization can be defined as a characteristic of the encoding transformation whereby samples of same higher level categories are likely to be transformed to distinct regions in the encoded space of the model. This spontaneous clustering by higher level concept can be observed in dAEN models directly by visualizing samples labeled by application category in encoded space.
In Fig.4 samples of several Internet applications, including: DNS requests (green, 500), Escale Newton (magenta, 220) and an Internet messenger (500, red) from Dataset B are plotted in the encoded space of a 50-3 model with non-categorized data of other categories (bottom plot, 10,000 samples, grey).
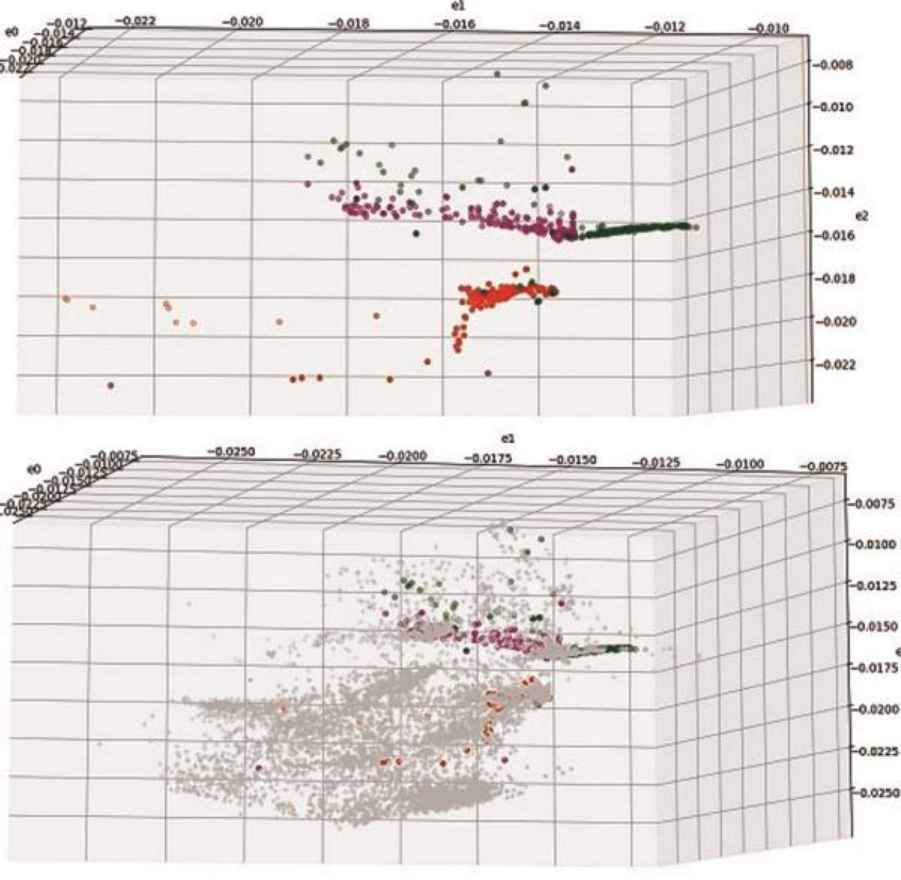
Categorized sample in encoded space
It can be seen that application samples are indeed transformed into distinct regions in the encoded space, though categorization parameters such as shape, size, density etc., may differ across applications. We found this effect for all application categories that were identifiable and had significant representation in the unsupervised training data including: BitTorrent, Gnutella file sharing applications, Xbox, Escale and Warcraft video games, NTP and DNS network applications, NNTP news protocol, several messaging applications and others. Same categorization effect was observed with labeled samples in Dataset A.
Categorization behavior of this class of models as well as other previously reported results on emergence of spontaneous information structures in deep learning systems merit separate in-depth investigation from both theoretical and empirical perspectives due to their importance for understanding principles of unsupervised information processing in deep learning systems as well as applications in information landscape based learning, of which SCL method developed in this study is one example.
4.4. Spontaneous Learning
Based on results presented in the previous sections that point to association between unsupervised spontaneous structure emergent in dAEN models and higher level categories we attempted to develop a learning method that would harness this unsupervised structure for more efficient learning. Specifically, we mean higher efficiency in several previously noted areas:
- (i)
Reduced requirement for ground truth training data
- (ii)
Iterative learning over a number of self-supervised and self-improving iterations
- (iii)
Spontaneity: learning when training data becomes available (environment driven) rather than with massive supervised data upfront
- (iv)
Flexibility: learning new and forgetting obsolete concepts without complete retraining of the model.
Spontaneous concept learning method (SCL) is based on detecting the unsupervised spontaneous structure in the encoded space with unsupervised clustering (Eq. 5) and using it, along with small streams of ground truth data representing trial and error iterations to construct a set of markers in the encoded space that would identify the concept-associated regions well enough for confident classification. It involves several stages:
- •
unsupervised learning: spontaneous structure is detected by structuring method and “synthetic” markers calculated from identified clusters;
- •
“awakening”, that registers first labeled samples of the new concept allowing to identify clusters in the encoded space associated with the concept and build first iteration of concept markers from identified concept clusters and labeled samples;
- •
trial and error iterations: the set of concept markers is updated based on results of trials with small streams of labeled data and classifier retrained on the updated set;
- •
reinforcement: check and maintain classification performance achieved in the learning phase.
We used a simple form of the method whereby synthetic markers were generated randomly within a small sphere around cluster centers and believe that refining it may considerably improve learning performance of the method.
Even in this simple form, the results in spontaneous learning were encouraging: for example, in learning runs with wake-up stream of 10 concept labeled samples followed by 10 trial and error iterations with 5 / 5 inconcept vs. non-concept labeled samples respectively, that translates to the total supervised training set of just 60 samples of the concept category, SCL could routinely achieve classification accuracy for the newly learned category above 95% and FPR below 5% with Dataset A. But the real challenge was in applying the method to live data of Dataset B that has significantly wider range of applications categories and data patterns.
In applying the method to samples from dataset B we faced the challenge of balancing markers for in- and out of concept clusters. With very small number of labeled samples used in SCL, the number of out of concept clusters that can be identified with trial samples was insufficient for good resolution, resulting in FPR of 15 – 20% and above. On the other hand, if the number of out clusters was not limited (that is, all clusters not identified as in-concept were considered to be in the out category), with large number of clusters that can be found in the live data, the number of out clusters greatly outnumbered in-concept ones, creating imbalance between in- and out-markers and resulting in better FPR but degradation of accuracy.
A working solution that was found was to limit the number of out-clusters to a fixed maximum, essentially, a parameter of the method. It allowed to achieve the optimal balance of in-concept accuracy and FPR for several tested application classes. Though this approach is somewhat crude we’re hoping that refining it would further improve learning performance of the method.
In Table 8, spontaneous concept learning was applied to samples of several Internet applications, followed by verification of classification accuracy with larger set of labeled application samples. The main parameters of the method are: 1) synt, the number of synthetic markers per cluster; 2) rsam, the number of ground truth samples of concept (in and out, each) per learning iteration; and the number of learning iterations (iter). In these tests rsam = 5, synt = 3 .. 10 and the number of iterations is 10 .. 15.
| Learning run | Class, Dataset | Learning / Total samples | Accuracy, FPR (%) (1) |
|---|---|---|---|
| A-Voice | Voice, A | 60 / 12,000 | 97.2, 6.4 |
| A-Web | Web, A | 60 / 12,000 | 98.6, 4.7 |
| B-NTP | NTP (2), B | 70 / 760 | 98.8, 6.1 |
| Newt-B | Newton (3), B | 70 / 220 | 92.8, 9.2 |
| MSM-B | MS Messenger | 70 / 1200 | 91.9, 7.8 |
| XBX-B | Xbox, B | 70 / 2300 | 88.7, 9.6 |
the mean of 10 learning runs, outliers removed
Network Time Protocol requests
Escale children learning and game console
Spontaneous Learning Results
It was encouraging to observe that the method could learn an entirely new concept from only a handful of ground truth samples (plus the unsupervised spontaneous structure in the encoded space) with good accuracy, especially given that dataset B is live Internet data with very broad variety of patterns – over 200 K samples representing over 4000 different application sources. In the NTP example, not only the model, being trained with just 70 / 60 of concept vs non-concept samples was able to classify correctly over 98% of concept samples out of ∼ 800, but also to resolve non concept samples from much larger pool (over 200 K samples, over 4000 different applications) with only 6% of false positives.
We also observed that using synthetic markers can improve accuracy of classification, in particular, FPR resolution. For example, with Newton samples from dataset B, the average FPR resolution of the method was improved by several percentage points by adding 3 – 5 synthetic markers per cluster (synt = 3 .. 5) while retaining good in-category accuracy.
Very light requirement for labeled data combined with ability to learn spontaneously and iteratively are clear strengths of SCL and landscape based learning generally that in our view merit further investigation and refinement with potential to approach learning efficiency of learning of biologic systems.
4.5. Conclusions
The results can be summarized as follows:
- (i)
Unsupervised training of deep autoencoder models studied here results in compact and structured representation of the input data space. This conclusion can be reached from shape and structure analysis with both datasets in Sec. 4.1.1 and investigation of structure and compression of data in unsupervised training, Section 4.1.2.
- (ii)
Some dAEN models can achieve high classification accuracy being trained with very small amounts of truth data (Sec. 4.2.1) pointing to possible correlation between unsupervised spontaneous structure and higher level categories in the input data.
- (iii)
Accuracy in classification is correlated with unsupervised training and is improved considerably over the course of training supporting the argument for correlation between unsupervised spontaneous structure and higher level categories (Sec. 4.2.2).
- (iv)
Visualization analysis in Section 4.3 directly supports the hypothesis that spontaneous structure emergent in unsupervised training reflects higher level categories in the input data.
- (v)
And that a method of spontaneous concept learning based on unsupervised spontaneous structure with iterative learning process and very light requirement for ground truth data is proposed achieving good classification performance with real world data (Section 4.4).
5. Discussion
5.1. Unsupervised Spontaneous Structure
According to observed results, training of dAEN models and possibly, more general class of deep neural network models in unsupervised mode can produce compact and structured representation of the input data in the encoded space that is correlated with general higher level categories. This observation led to the following hypothesis of “spontaneous categorization”:
Models studied here provide an example of a general information processing strategy that allows information processing systems to package and store data more efficiently by separating general features (concepts) and transforming them into separate compact regions in the effective information space of the model.
This finding can be an argument in support of the “bottleneck” principle of deep learning proposed by Tishby et al. in [6]. One can conjecture that strong information flow through inner layers of the model during unsupervised training strips off irrelevant or random elements leaving information structure, a sort of “skeleton” of general features or concepts that were present in the original data. The idea behind the layout of the dAEN models in this study was that by inflating the first inner layer, then reducing it at a high ratio to the central layer may increase information flow through the focal point of the model, and result in a more pronounced encoded structure. And we did observe indirect evidence of such strong information flows in a number of runs where one or more of Relu neurons in the encoded layer were “knocked out” during training resulting in flat output of the model in the corresponding dimension. Hence, spontaneous categorization observed in our experiments may indeed be related to information flows during training phase.
In the future studies we shall attempt to provide both theoretical and empirical arguments for spontaneous emergence of unsupervised structure in deep learning models. We believe that it may have important implications for designing general purpose, adaptive machine learning systems capable of learning new concepts directly from the environment.
5.2. Landscape Based Learning
Triggered, guided and reinforced by the environment spontaneous concept learning is an exciting possibility that can bring machine learning closer to learning processes of biologic systems. Information landscape learning, based on emergent structure in the information space of deep autoencoder models, can address several long-standing challenges in traditional machine learning:
- (i)
it points a direction for development of flexible general learning methods that are capable of learning directly from the environment;
- (ii)
it has minimal requirement for ground truth data that doesn’t need to be available all at once for learning process to begin and proceed;
- (iii)
it allows to train models iteratively in a continuous trial and error process reminiscent of learning of biologic systems;
- (iv)
it leads naturally to a flexible and adaptable higher level category structure where new features can be added (and old ones forgotten) without retraining of the system.
Further investigation may lead to more versatile algorithms for construction of effective concept markers in the effective encoded space of learning models resulting in improved learning performance of landscape based methods.
5.3. Parallels with Biologic Systems
In the context of the study the parallels with information processing strategies of biologic systems are thrilling. Self-supervised reproduction of inputs may have immediate benefits for a biologic system in correct interpretation and response to the changes in the environment that can be critical for survival. Is it possible that networks similar to autoencoder by function if not by architecture developed first as a mean to carry information about the environment deeper into the system, with learning of more general concepts emerging as a by-product of natural development of information structure in the inner layers of such networks?
Another essential insight that these findings can offer is relatively straightforward explanation for forgetting, an important learning function without which true general learning may not be feasible. In SCL, forgetting a concept means only discarding its classifier and markers (for example, in this study, some 100 points in the encoded information space) and doesn’t require retraining of the system, while in traditional machine learning it’s quite challenging to forget a part of the category space a model was trained with without retraining of the model.
In this approach, information structure learned in unsupervised training plays the role of ground foundation for subsequent learning by trial and error. These findings therefore may provide insights for further research in neuroscience and learning of biologic systems.
5.4. Future Work
It would be both interesting and challenging to attempt to apply the results of this study to more complex deep learning models and other types of data such as, ultimately, visual recognition. A critical and still open question in such a program would be how to construct the effective information space from multiple layers of a deep model with numerous and sparse activation layers.
The results reported by Le et al. on spontaneously emerging concept sensitive neurons may point in this direction, however, the accuracy of recognition hints that perhaps another, overlay layer or even a secondary network would be needed to collect inputs of multiple layers and combine them for confident resolution. In our models the layout of the encoded space was imposed by the architecture of the model itself and the summation layer performing structure detection was modeled by simple clustering algorithm. This may not and likely would not be the case for deep and sparse neural networks requiring further analysis and insights to construct effective encoded space where structure analysis can be performed.
Methods and algorithms of spontaneous concept learning certainly need further refining. In particular, more advanced strategies for construction of effective markers in the encoded space can be developed to improve learning performance of landscape based methods.
Finally, it would be exciting to explore the parallels between general learning of machine and biologic systems. Are these similarities only superficial, or reflect similar processes and architectures of information processing in machine vs biologic networks? These questions can be approached from both machine learning and neuroscience directions.
Acknowledgements
We’d like to thank colleagues at Solana Network Engineering for valuable discussions and specifically prof. Bis Nandy, Solana Networks and Carleton University (Ottawa) for reviewing this work and offering valuable feedback.
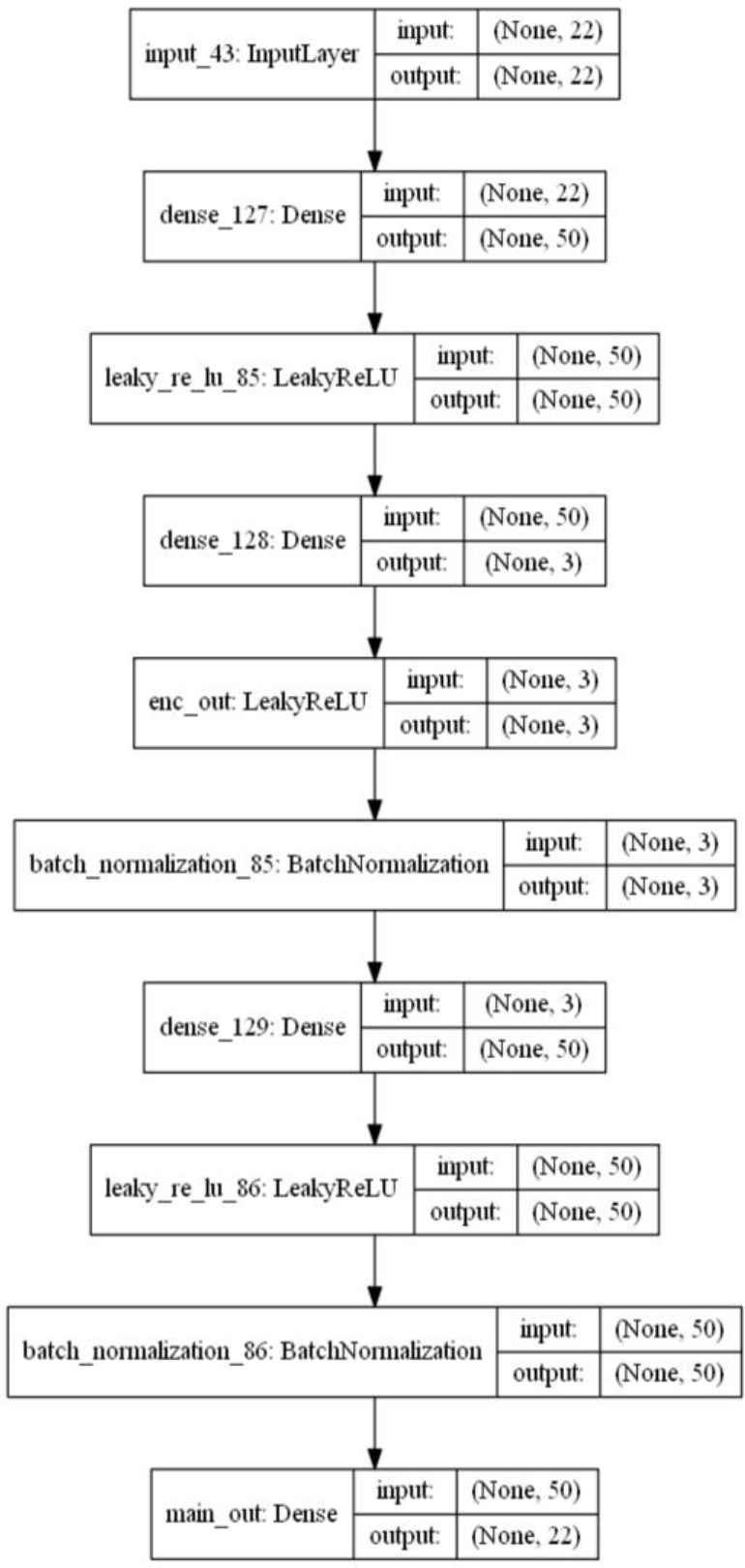
Appendix A. Model Layout
Detailed layout diagram of a dAEN 50-3 model
References
Cite this article
TY - JOUR AU - Serge Dolgikh PY - 2018 DA - 2018/11/01 TI - Spontaneous Concept Learning with Deep Autoencoder JO - International Journal of Computational Intelligence Systems SP - 1 EP - 12 VL - 12 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.2018.25905178 DO - 10.2991/ijcis.2018.25905178 ID - Dolgikh2018 ER -
