A Genetic Algorithm with New Local Operators for Multiple Traveling Salesman Problems
- DOI
- 10.2991/ijcis.11.1.53How to use a DOI?
- Keywords
- Multiple Traveling Salesman Problem; Genetic Algorithm; Branch and Bound algorithm; Local operators
- Abstract
Multiple Traveling Salesman Problem (MTSP) is able to model and solve various real-life applications such as multiple scheduling, multiple vehicle routing and multiple path planning problems, etc. While Traveling Salesman Problem (TSP) focuses on searching a path of minimum traveling distance to visit all cities exactly once by one salesman, the objective of the MTSP is to find m paths for m salesmen with a minimized total cost - the sum of traveling distances of all salesmen through all of the respective cities covered. They have to start from a designated depot which is the departing and returning location of all salesmen. Since the MTSP is a NP-hard problem, a new effective Genetic Algorithm with Local operators (GAL) is proposed in this paper to solve the MTSP and generate high quality solution within a reasonable amount of time for real-life applications. Two new local operators, Branch and Bound (BaB) and Cross Elimination (CE), are designed to speed up the convergence of the search process and improve the solution quality. Results demonstrate that GAL finds a better set of paths with a 9.62% saving on average in cost comparing to two existing MTSP algorithms.
- Copyright
- © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Traveling Salesman Problem (TSP) is a widely studied optimization problem. Given a set of cities and the distances between them, the TSP is defined as a path searching problem for a salesman to visit all cities exactly once, starting and ending at the same city. The objective of a TSP is to minimize the traveling distance of the salesman. Many real-life applications can be modeled as a TSP, such as the printed-circuit-boards drilling problem 1, the order-picking problem2 and the wallpaper minimization problem 3.
Multiple Traveling salesman Problem (MTSP) is an extension of the TSP, which has more than one salesman deployed concurrently to visit the cities. All salesmen depart from and return to the same depot. Except for the depot, each of the cities can only be visited by exactly one salesman. Minimizing the total cost of all paths taken by the salesmen is the goal of an MTSP. Some typical applications of the MTSP are path planning 4, scheduling 5 and school-bus routing 6.
Our work is motivated by the multiple quadcopter paths planning problem. Compared to fixed-wing aerial vehicles, quadcopters have different aerodynamics. As the flight time is highly limited by the internal batteries, an effective path planning algorithm can help to accomplish as many tasks as possible within a deployment of multiple quadcopters. Such a problem can be modeled as a three-dimensional MTSP.
The MTSP can also be extended with different constraints or objectives, such as the multiple objective 7, multiple depot 8, multiple vehicle routing problem 10, traveling salesman problem with multiple Stacks?etc. Designing efficient algorithms for the MTSP can also benefit these problems. Currently, the existing works mostly focus on modeling real-life scenarios into MTSP but only a few have the potential to solve the MTSP efficiently.
Because the MTSP is a NP-hard problem 11, there is no known polynomial-time algorithm for the MTSP. Therefore, it is more realistic to resolve the problem by heuristic algorithms. In this paper, an efficient algorithm based on genetic algorithm(GA), called Genetic Algorithm with Local operators (GAL) is proposed and developed to solve the MTSP. The major contributions of this paper are: 1) we have designed a GA-based algorithm for solving MTSPs effectively and; 2) we have proposed two novel local operators for the GA to improve its convergence speed.
We organize the paper as follows. Section 2 reviews the related research. In Section 3, the problem definition and formulation are discussed. The algorithm is described in detail in Section 4. Experimental results and discussions are reported in Section 5. The conclusion is presented in Section 6.
2. Related Work
The practical algorithms to solve the MTSP can be categorized into exact and meta-heuristics algorithms. The selection of an algorithm mainly depends on the problem size. Exact algorithms are suitable for small-scale problems to get the optimal solution. Due to the NP-hard nature of the MTSP, heuristic algorithms are more popular in solving large-scale MTSPs. The cutting-planes algorithm 12 was used to optimally solve the problem with less than 100 cities.
An extended simulated annealing algorithm 13 was developed to solve augmented TSPs and MTSPs. The proposed algorithm does not require transformation 14 from an MTSP form to the standard TSP form before solving the problem.
A modified Genetic Algorithm (GA) 15 with a new crossover framework, which balances the computation time and the quality of the solution, was introduced in the paper to model the hot rolling problem into the MTSP and handle by GA.
A two-part chromosome encoding scheme 16 for GA was proposed. By eliminating redundant solutions, the size of solution space reduces and convergence is improved. The experiments indicated that this encoding method produces the best solution, comparing to the existing encoding methods with the same execution time. For this reason, subsequent works on solving MTSPs using GA mostly adopted this chromosome encoding method in their work.
GA with 2-opt local operator 17 for solving the MTSP was invented. In the paper, the initial population is generated using the nearest neighbor method to introduce greedy initial population to enhance the convergence speed in the early stages. 2-opt local operator was adopted to avoid pre-mature convergence of the algorithm. Various mutation and crossover operators for MTSPs were designed and compared by the authors 18. The result showed proper operator design can boost the performance.
When the number of cities in an MTSP is relatively large (>500 cities), Ant Colony Optimization (ACO) 19 was likely to produce better solutions comparing to GA on MTSPs. The result had been further improved by using the elite ACO 20. The initial paths are generated by the Sweep Algorithm to cluster the cities by the polar coordinate angles between the cities and the depot, which creates a greedy initial population. A 3-opt local operator is also applied to speed up the convergence. To enhance the capability to escape from local optimum points, the same authors designed an insert, swap, and 2 opt algorithm 21. Five local search schemes 22 were introduced by the authors to improve the result without much increased time complexity.
Inspired by the existing works mentioned above, the work done in this paper further improves the convergence speed of using GA to solve the MTSP with two novel local operators.
3. Methodology
3.1. Problem Definition and Formulation
The MTSP is defined as follows: given m salesmen, n cities and the visiting cost C (an n by n matrix) between the cities, search the visiting sequences for the m salesmen such that the total visiting cost of all salesmen is minimized. Each city can only be visited exactly once by one of the salesmen. All salesmen start from and return to the same depot (which is not counted as a city to be visited). Each salesman has to visit at least 1 city and at most P cities.
The assignment-based integer programming representation for the MTSP is presented as follows: The cities and the visiting routes can be represented as an undirected and complete graph G = (V,E) which contains a set V of n vertices (the cities) and a set E of n2 (the routes between cities) edges, where V0 ∈ V is denoted as the depot for the salesmen. The rest of the n − 1 vertices V \ {V0} represent the cities to be visited. Each vertex Vi is associated with a position (xi,yi) in the Cartesian-coordinate system. Eij ∈ E is the edge traveling from vertex Vi to Vj associated with a traveling cost Cij, which is the Euclidean distance between the vertices Vi and Vj. Therefore, the visiting cost is symmetric, i.e. Cij = Cji.
A binary variable Xij is defined to indicate the usage of an edge from vertex Vi to Vj in the solution. It equals to 1 if edge Eij is included in the solution path and 0 otherwise. P is the maximum number of cities that one salesman can visit in a path. Therefore, the problem is formulated as
Constraints (2) and (3) ensure that there are exactly m salesmen departing from and returning to the depot. Each vertex is entered and exited by exactly one salesman, as ensured by constraints (4) and (5). Constraint (6) is called the subtour elimination constraints 23, which prevents the paths from being formed without depot, where ui represents the number of cities visited from the depot up to vertex i for any salesman.
3.2. Genetic Algorithm Solution
GA is a mulitpoint stochastic search algorithm which was first proposed by Holland 24. It simulates the natural evolution process to generate solutions and search the optimal solution(s) for optimization problems. Considerable amount of researches on using GA to solve TSP or MTSP have been done successfully with satisfactory results.
In GA, the candidate solution is usually encoded in a numeric vector called ’chromosome’. Each number inside the chromosome is considered as a gene. Then a set of individuals containing the randomly generated chromosomes forms a population. Each individual is evolved by selection, mutation and crossover operators. The mutation operator randomly changes one or more genes to keep the diversity of the population, where the crossover operator attempts to combine the advantages of the parent chromosomes to form the child chromosome. A fitness value is computed to evaluate the quality of a chromosome. For the MTSP, the fitness value equals to the total traveling costs of all salesmen. Hence, the optimal solution is found when the fitness value is minimized.
Our proposed algorithm is also a GA. The complete process of the proposed algorithm is shown in Figure 1. The termination criteria can be set as fixed number of generations, fixed execution time or termination time if no significant improvement can be made compared to the preceding generations.
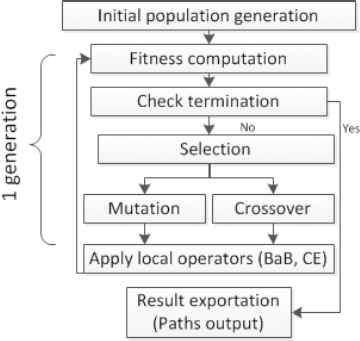
Evolution process the proposed GA algorithm
3.2.1. Chromosome Representation
There are several ways to encode an MTSP solution into a chromosome, including one chromosome15, two chromosomes 25, two-part chromosome 16 etc. With the condensed solution space, experimental results have demonstrated that two-part chromosome performs the best in terms of convergence speed and quality of solution. Hence, two-part chromosome representation is adopted in this work.
Each chromosome is composed of a numeric vector with length n + m − 1. The first n − 1 genes represent the visiting permutation for the salesmen. The remaining m genes represent the number of cities for each salesman to visit. One of the chromosome representation examples is shown as follows, where Gi represents each city visited and Lj is the number of cities visited by salesman j.
Because all salesmen must depart from and return to the depot (V0), this city is not included inside the chromosome to save the memory usage. A chromosome representation example with 11 cities and 3 salesmen is illustrated in Figure 2. In this example, the first salesman is responsible for visiting 5 cities as stated in the second part of the chromosome. The visiting cities’ permutation of the first salesman is 0 (Depot)→ 9 → 8 → 1 → 3 → 6 → 0 (Depot). The visiting cities’ permutation of the second salesman is 0 (Depot) → 7 → 2 → 10 → 0 (Depot). Finally, the visited cities’ permutation of the third salesman is 0 (Depot) → 4 → 5 → 0 (Depot).
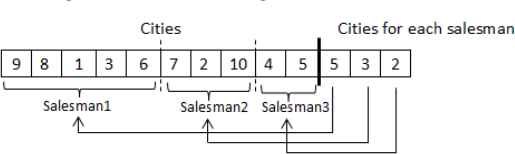
An example of two-part chromosome representation for 10 cities and 3 salesman from the same depot
3.2.2. Initial Population Generation
A better quality of initial population can improve the search efficiency since random permutation of cities is unlikely to produce informative routes in the evolution. A method modified from the Sweep Line algorithm 20 is adopted in our work. The algorithm generates a sweep line (dotted line in Figure 3) from the depot to an arbitrary city. By sweeping the line clockwise with the depot as center, a path ordered by the polar angle is built as shown in Figure 3. This approach assumes that if the cities have similar polar coordinate angles, they tend to be closer to each other.
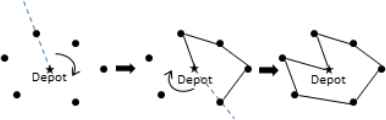
An initial path generated by the Sweep line algorithm
Half of the initial population contain the generated paths using the Sweep Line algorithm, while the remaining paths are randomly generated as random permutations to maintain the diversity in the population. After that, for each chromosome produced by the Sweep Line algorithm, a segment of genes (i.e. 1% genes of the chromosome) is selected randomly, the genes inside the segment are re-ordered using the nearest neighbour method as follows: For the genes in the selected segment, one of the genes is chosen randomly as the starting gene. For the next gene, the gene closest to the previous gene in the selected segment will be chosen. When all the genes in the newly constructed segment are re-ordered, they replace the original segment in the chromosome.
Next, the number of cities for each salesman encoded in the second part of the chromosome are initially evenly distributed. It avoids the paths having excessive lengths at the beginning. The size of the initial population is much larger than the population size of later generations, and only 1.5% (50 over 3000) of the initial chromosomes are selected to be evolved based on their diversity and fitness value.
3.2.3. Genetic Operators
Genetic operators are essential for GA to evolve the chromosomes. They significantly influence the search ability and convergence speed. Proper design of the genetic operators can further prevent pre-mature convergence, which means the solution is stuck in a local optimum. Hence, the choice of proper genetic operators is essential.
As aforementioned, there are constraints on the final solution. The cities inside the first part of the chromosome must appear only once to ensure that each city is visited only once. Besides, the sum of the values in the genes of the second part of the chromosome must be equal to the total number of cities to be visited. Also, there is a maximum number of cities for each salesman to visit. Due to these constraints, canonical genetic operators cannot be directly adopted in this chromosome encoding scheme. Therefore, modified genetic operators are used to evolve the chromosomes.
Since the first and second parts of the chromosome contain different information and should not be mixed, separate genetic operators for each part are required.
There are two mutation operators for the first part of the chromosome, which are the random swap and the reverse swap operators. For the random swap operator, two random distinct positions (Gi and Gj) are selected, where i ≠ j, the genes in these two positions are exchanged. For the reverse swap operator, two random distinct positions are selected to define segment, the position of the genes inside the segment are reversed. Examples are shown in Figures 4 and 5 respectively.
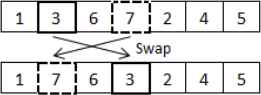
Random swap operator
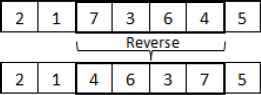
Reverse swap operator
For the second part of the chromosome, which controls the number of cities for each salesman to visit, random distribution mutation is applied as mutation operator. Two random distinct positions (i and j, where i ≠j) from the second part of the chromosome are selected. The gene in Gi will be incremented by one, and the gene in Gj will be decremented by one as shown in Figure 6. Then we have to check whether the result chromosome still fulfills the number of cities per salesmen constraint, which means Gi >= 1 and Gj <= P, where P is the maximum number of cities allowed to visit for each salesman.
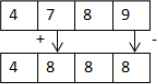
Random distribution mutation operator for the second part of a chromosome
In the example shown in Figure 6, originally, salesman 2 has to visit 7 cities while salesman 4 has to visit 9 cities. After mutation, salesman 2 now visits 8 cities while salesman 4 visits 8 cities.
Edge recombination crossover operator 26 is modified to crossover the first part of the chromosome. This operator has been validated to be efficient in solving the TSP. The key idea of this operator is that if an edge appears in both parent chromosomes, it is believed to be a good edge and has higher chance to be present in the optimal solution.
The neighboring information is stored in an edge table. The table size is n * 4, where each row represents a vertex, and the columns contain the neighboring vertices information of that vertex. As each vertex appears once in both parent chromosomes, and it contains at most two neighbours in each parent chromosome, hence the column size is determined to be 4. The detail of this operator is presented in Algorithm 1.

Edge recombination crossover operator
3.2.4. Local Operators
In the general GA evolution process, the convergence power is determined by the mutation and crossover operators. Local operators are used in this work to boost the convergence rate. The operators use local search techniques to introduce greedy chromosome segments into the population. To prevent premature convergence, the operators should only be executed in between specific generations (e.g. 100 generations) and inside a small portion (e.g. to the top 5 individuals only) of the population. We have designed two local operators to optimize the paths at different scales. The Cross Elimination operator (CE) works in a global manner, it can reduce the total traveling cost by rearranging the visiting order of a large number of cities. In addition, the Branch-and-Bound operator (BaB) targets at producing an optimal path for a small segment of the cities from one salesman path.
Cross Elimination Operator (CE) This local operator actively searches for the crosses formed inside the paths, and attempts to remove them by reordering the cities sequence. The fundamental concept of CE operator is similar to the 2-opt operator 27. If a cross is formed inside a path(the sequence of cities visited by one salesman), it means the path is not optimal. The cross searching technique of CE is based on the Bentley Ottmann algorithm 28. It is a sweep-line algorithm for detecting the crosses of a set of line segments. The crosses in the MTSP can be classified into two types, namely the intra salesman path crosses and the inter salesmen path crosses. An intra salesman path cross is formed by the edges in a single salesman path, while an inter salesmen path cross is formed by the edges across two different salesmen paths.
The CE operator needs to be performed carefully to avoid incorrect result from being produced. It is because solving a cross may generate new cross(es) or remove other existing cross(es). An example is shown in Figures 7 and 8. Therefore, before solving a cross, it should be checked to see whether the cross still exists in the path or not. All the newly generated crosses will be handled in the next cycle of the process. To determine the cross solving order, a list containing the estimated cost saving of solving each cross is created and sorted by descending order. The elimination will begin from the cross which maximizes the cost saving first.
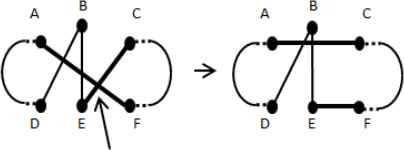
Illustration of an intra salesman cross solving process. Suppose we are solving the cross formed by EAF and ECE. After solving this cross, cross formed by EAF ,EBD and EAF ,EBE are also eliminated.
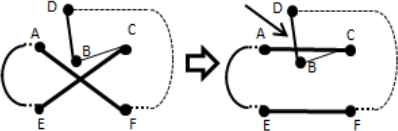
Illustration of an intra salesman cross solving process. We can see that a new cross is formed by EAC and EBD after solving the cross formed by EAF and EEC.
Solving the intra salesman path crosses is always feasible as the number of cities visited by each salesman remains unchanged and total traveling cost always decrease. For the inter salesman path cross, the solving process is more complicated. There exists two different options to handle it, as shown in Figure 9 to 11. It is possible that the new solution violates the path length constraint (i.e., each salesman has to visit at least 1 city and at most P cities). We can see that one of the newly generated paths becomes longer while the other path becomes shorter in Figure 11, that means one salesman will visit 5 cities and the other salesman will visit 3 cities. Hence, when handling inter salesman path crosses, we need to consider whether the result can still satisfy the path length constraints or not and which way to solve the cross such that most costs are saved. This can be achieved by estimating the number of cities and the fitness of the paths after cross solving respectively.
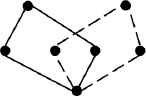
Input path
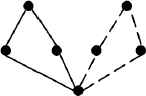
Solution 1 by Cross Elimination
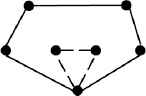
Solution 2 by Cross Elimination
After a solving sequence is built, crosses solving can be executed in order. As stated in the previous paragraph, the crosses in the path may change after a cross is solved, some new crosses may be formed and are not detected by the initial checking. The cross solving process will iterate for several cycles (at most 5 cycles) or stop when no major improvement (at least 1% improvement in fitness) can be achieved.
Branch-and-Bound Operator (BaB) This local operator is based on the Branch-and-Bound algorithm. The algorithm is designed for searching the optimal solution of discrete and combinatorial optimization problems. It consists of a systematic enumeration of candidate solutions by the means of state-space search: the set of candidate solutions form a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against the upper and/or lower estimated bounds on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm.
Previous works 29 have applied Branch-and-Bound to calculate the optimal solution of a TSP. Since the algorithm has high time complexity (O(n3) in average 30), it requires an excessive amount of time to find the solution when the number of cities is large. In this local operator, the Branch-and-Bound algorithm is only applied on a subset of a single salesman path. The subset is randomly selected from a continuous segment of a single salesman path. This reduces the running time of the operator, and introduces locally optimal path to the population. An example is shown in Figure 12. The BaB operator is applied to the cities marked with solid circles. The vertices between those cities are reordered by Branch-and-Bound to achieve a locally optimal TSP path. From our testing, we randomly select a total of 10% genes to be processed by the BaB piece by piece. Each piece has at most 5 cities to balance the computational time and performance.
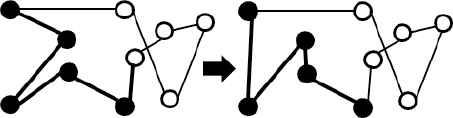
An example to applying BaB operator to a single salesman path.
4. Evaluation
4.1. Experimental Setting
In this section, we will evaluate the performance of GAL. Firstly, the experiments focus on measuring the convergence power of the new local operators. Secondly, we compare GAL with the existing MTSP solving approaches with respect to computational time and solution quality.
GAL is coded in Java and compiled with JDK 1.8. Experiments are run using one single thread on a PC with Intel Core i7-3370 CPU @3.4 GHz and 32 GB RAM. Each test case is run for 20 times to reduce random fluctuations in evaluation. A problem set from the TSPLIB 31 is used as benchmark in the experiments. The problem set contains 6 problems with the numbers of cities ranging from 76 to 1002. In this benchmark, there is a maximum cities constraint, which sets an upper limit on the number of cities each salesman can visit. The benchmark details are listed in Table 1. Selected parameters for GAL are listed in Table 2.
| Instance | No of cities | Number of salesmen | Max cities |
|---|---|---|---|
| Pr76 | 76 | 5/10/15 | 20 |
| Pr152 | 152 | 40 | |
| Pr226 | 226 | 50 | |
| Pr299 | 299 | 70 | |
| Pr439 | 439 | 100 | |
| Pr1002 | 1002 | 220 |
Parameters of the benchmark problems
| Parameters | Values |
|---|---|
| Initial Population Size | 3000 |
| Population Size | 50 |
| Random Swap Rate | 30% |
| Reverse Swap Rate | 10% |
| Crossover Rate | 40% |
| Random Distribution Rate | 20% |
| Local Operator | Every 100 generations to the top 1,2,4 individuals CE ran before BaB |
Parameters for GAL
4.2. Comparing Different Local Operators under different numbers of salesmen
In this paper, two novel local operators - BaB and CE are formulated to speed up the convergence speed of the proposed algorithm. This experiment aims at comparing the convergence power of the operators under different numbers of salesmen. Hence, we set the maximum number of generations to a fixed value, which is used as the termination criterion. The results are reported in Table 3. Combining both local operators (BaB and CE) in GAL obtains the best-fitness solution compared to other settings in most of the test cases. The fitness is defined as the sum of the salesmen’s path costs, which is the smaller the better.
| Number of salesmen | 5 | 10 | 15 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Problem | Local Operator | Best | Avg | Worse | Time | Best | Avg | Worse | Time | Best | Avg | Worse | Time |
| Pr76 | None | 157,590 | 168,840 | 172,820 | 4.20 | 208,559 | 220,259 | 258,054 | 5.02 | 242,827 | 272,736 | 296,349 | 5.30 |
| BaB | 162,722 | 167,697 | 172,089 | 6.60 | 205,042 | 225,023 | 243,357 | 7.66 | 252,958 | 272,145 | 289,329 | 7.80 | |
| CE | 153,880 | 164,661 | 171,279 | 4.90 | 179,156 | 186,317 | 190,640 | 6.65 | 219,246 | 226,224 | 233,538 | 6.54 | |
| CE+BaB | 152,278 | 166,138 | 170,752 | 6.80 | 177,806 | 182,381 | 188,570 | 8.29 | 218,901 | 223,927 | 229,559 | 8.77 | |
| Prl52 | None | 123,907 | 138,088 | 143,775 | 16.70 | 205,244 | 228,736 | 244,971 | 19.10 | 249,601 | 289,744 | 311,514 | 19.13 |
| BaB | 124,714 | 131,109 | 137,615 | 27.00 | 221,838 | 234,944 | 244,843 | 27.80 | 275,591 | 304,915 | 335,748 | 28.11 | |
| CE | 118,106 | 132,395 | 149,340 | 19.40 | 134,161 | 136,228 | 145,139 | 22.09 | 154,249 | 164,741 | 172,612 | 21.27 | |
| CE+BaB | 116,620 | 131,674 | 138,091 | 28.00 | 132,917 | 141,993 | 156,247 | 32.14 | 156,131 | 164,321 | 174,784 | 29.49 | |
| Pr226 | None | 152,016 | 156,893 | 163,805 | 46.70 | 224,132 | 247,699 | 270,164 | 51.95 | 284,113 | 324,268 | 343,743 | 51.12 |
| BaB | 149,068 | 155,574 | 159,439 | 77.00 | 220,032 | 251,155 | 272,261 | 81.43 | 308,117 | 340,139 | 363,043 | 81.81 | |
| CE | 153,409 | 157,120 | 163,848 | 52.60 | 168,428 | 172,193 | 177,955 | 58.84 | 181,235 | 188,813 | 194,446 | 58.74 | |
| CE+BaB | 148,040 | 156,629 | 162,329 | 75.60 | 167,782 | 171,338 | 175,371 | 85.43 | 180,431 | 188,489 | 194,800 | 82.13 | |
| Pr299 | None | 76,469 | 78,872 | 80,880 | 78.00 | 116,104 | 121,429 | 123,826 | 82.01 | 156,812 | 163,144 | 168,464 | 83.17 |
| BaB | 73,177 | 77,676 | 80,093 | 120.90 | 118,797 | 121,983 | 123,236 | 117.67 | 152,991 | 160,755 | 170,830 | 123.88 | |
| CE | 75,957 | 78,217 | 80,945 | 86.90 | 76,924 | 81,323 | 87,477 | 95.71 | 84,266 | 87,490 | 94,649 | 101.94 | |
| CE+BaB | 75,145 | 77,413 | 78,793 | 123.10 | 75,450 | 78,999 | 83,613 | 132.31 | 85,515 | 88,526 | 91,800 | 134.14 | |
| Pr439 | None | 146,793 | 152,224 | 158,832 | 184.70 | 204,525 | 209,376 | 217,517 | 185.17 | 264,348 | 270,185 | 280,318 | 209.93 |
| BaB | 141,951 | 146,436 | 149,874 | 300.00 | 202,714 | 207,095 | 212,185 | 283.39 | 258,487 | 267,122 | 274,980 | 279.41 | |
| CE | 142,800 | 148,416 | 154,342 | 215.20 | 146,162 | 151,636 | 157,471 | 211.26 | 155,004 | 159,609 | 167,336 | 211.58 | |
| CE+BaB | 141,180 | 147,389 | 151,975 | 295.70 | 144,527 | 151,392 | 160,634 | 301.25 | 149,649 | 155,512 | 161,226 | 315.70 | |
| Prl002 | None | 358,316 | 375,882 | 400,960 | 793.70 | 441,641 | 449,855 | 461,639 | 800.90 | 538,708 | 550,605 | 558,926 | 812.93 |
| BaB | 339,890 | 348,712 | 365,834 | 1,154.80 | 425,578 | 435,109 | 444,763 | 1,182.24 | 529,951 | 535,035 | 540,143 | 1,149.55 | |
| CE | 341,752 | 349,258 | 358,935 | 864.30 | 366,273 | 371,649 | 378,521 | 894.75 | 386,697 | 393,286 | 400,016 | 888.89 | |
| CE+BaB | 332,652 | 338,580 | 346,574 | 1,224.50 | 347,126 | 360,284 | 368,582 | 1,298.28 | 379,677 | 383,360 | 389,104 | 1,240.62 | |
Fitness comparison with different local operators and number of salesmen
The convergence curves with 5 agents are shown in Figures 13 and 14. With a larger problem size, the solutions converge faster when both operators are used. The average fitness values are improved by 4.1%, 28.1%, 36.7% with 5, 10, 15 salesmen respectively compared to the results without local operators.
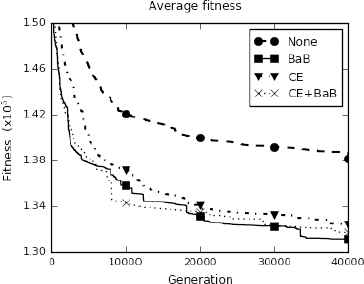
Convergence diagram with 152 cities with 5 salesmen
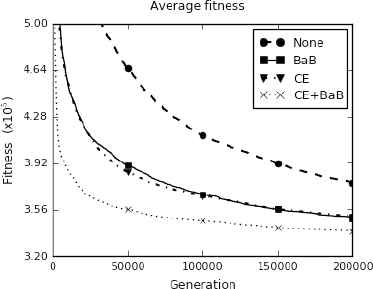
Convergence diagram with 1002 cities with 5 salesmen
From the experiment, we observed BaB works poorly with a small ratio of number of cities / number of salesmen, which means for each salesman visiting path, it is more likely to be a short path. We believe such kind of path may achieve local optimum in early GA stage. Hence, applying BaB will not help, since MTSP global optimization requires inter-salesmen cities exchange.
To boost GAL, a threshold for BaB can be introduced. When the fitness improvement obtained by BaB is lower than a threshold (k %), it will be disabled for certain cycles. It will help to save time and avoid creating disarrangement for finding better solution by cities exchange.
The rates of local operators can also be adjusted to fit different problems. If the application is time critical, BaB can be disabled to obtain the acceptable results in the quickest way. If the computational resource and time are adequate, the application is cost critical, using both operators will bring the best benefit to the outcome.
4.3. Comparing with Existing Algorithms
In this section, we compare the performance of the proposed algorithm - GAL against two other existing approaches - Modified Ant Colony Optimization(MACO) 19 and Elite Sweep line Ant Colony Optimization (EACO) 20. Both approaches use Ant Colony Optimization (ACO) to handle MTSP. MACO solves the MTSP by ACO with the ability constraint, where EACO applies Sweep Line Algorithm to improve the initial paths, and uses 3opt local operator to speed up the algorithm. Both of them claimed that their results are the state-of-the-art in the benchmark problems. In this experiment, the parameters setting are listed in Table 2. The algorithm stops when there is no improvement on the fitness value of the best individual in the successive 10000 generations, which means our algorithm reaches the convergent situation.
As those papers only include the case with 5 salesmen, the experiment in this section will also be limited to 5 salesmen only. The experimental results are shown in Table 4. Comparing to existing approaches, GAL can obtain the best fitness. The average fitness values are also greatly improved in the Pr226, Pr299, Pr439 and Pr1002 cases, which are the 4 largest problems. Our approach is always faster than MACO. Although the running time of our method is slightly longer than EACO, the average fitness has obvious improvement in comparison (9.62%).
| Problem size | Algorithm | Best fitness | Average fitness | Time (in seconds) |
|---|---|---|---|---|
| 76 | GAL | 153389.9 | 162810.6 | 17.7 |
| EACO | 157495 | 157562 | 19 | |
| MACO | 178597 | 180690 | 51 | |
| 152 | GAL | 115873.8 | 128053.4 | 47.4 |
| EACO | 127791 | 128004 | 41 | |
| MACO | 130953 | 136341 | 128 | |
| 226 | GAL | 148050.6 | 156542.3 | 76.6 |
| EACO | 167665 | 168156 | 62 | |
| MACO | 167646 | 170877 | 143 | |
| 299 | GAL | 72949.3 | 77481.6 | 108 |
| EACO | 81998 | 82195 | 65 | |
| MACO | 82106 | 83845 | 288 | |
| 439 | GAL | 143785.4 | 147710.7 | 269.5 |
| EACO | 161725 | 162657 | 95 | |
| MACO | 161955 | 165035 | 563 | |
| 1002 | GAL | 334350.6 | 341303.9 | 1524 |
| EACO | 379871 | 381654 | 186 | |
| MACO | 382198 | 387205 | 2620 | |
Comparison of the proposed algorithm and the existing MTSP solving algorithm with 5 salesmen
5. Discussion
In the experiments, we found that inter-crosses could exist in a better solution. An example is shown in Figures 15 and 16. Although no inter-cross is found in the paths of Figure 16, the fitness is 10.07% worse than the path of Figure 15. We suspect this is due to the constraint of maximum cities visited per salesman. From the observation, elimination of inter-cross may not always be a good idea.
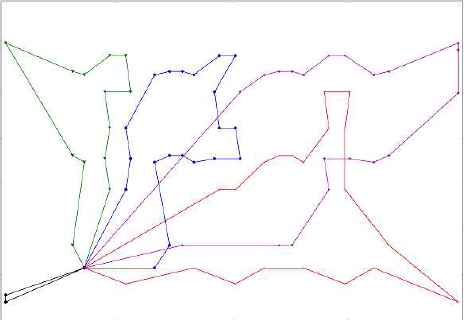
Path visualization with 76 cities - Better solution (Fitness : 153376)

Path visualization with 76 cities - Locally optimal solution (Fitness : 170558)
Hence, the timing for applying this local operator should be carefully selected. For example, when the solution chromosome is stuck for some generations, this operator can instantly improve the chromosome quality. On the other hand, maintaining the diversity of population reduces the chance of getting into this sticking situation. In addition, with the BaB operator, locally optimal solution has a chance to jump out of the local optimum. The CE operator is safe to use with such precautions in place.
Although the GA 32 described in that paper also handles the same problem instance, it requires precomputed initial population from a TSP path using Lin and Kernighan operators 33. Our proposed algorithm is suitable for making solution from scratch, in which pre-computed information is not available. Hence, the algorithm is not comparable with our proposed work.
6. Conclusion
In this paper, a novel MTSP solving algorithm, called Genetic Algorithm with Local operators (GAL) has been proposed and developed. The new local operators BaB and CE have been successfully deployed to generate high quality results in a short computation time. We have also compared the performance of our work with those of the existing approaches. Our algorithm has made improvement in the search ability and speed.
For future study, as GA can be run in parallel, the proposed method can be further improved by using parallel GA design for real time applications. Furthermore, the local operators can be applied to other variations of MTSP-like problems, like minmax MTSP 34 and multiple objective MTSP 35 to find better solution efficiently.
Acknowledgment(s)
This research was supported by the Vice-Chancellor’s one-off support of The Chinese University of Hong Kong. The authors would like to thank Leung-Yau Lo and Kwan-Yau Cheung for their assistance.
Cite this article
TY - JOUR AU - Kin-Ming Lo AU - Wei-Ying Yi AU - Pak-Kan Wong AU - Kwong-Sak Leung AU - Yee Leung AU - Sui-Tung Mak PY - 2018 DA - 2018/02/05 TI - A Genetic Algorithm with New Local Operators for Multiple Traveling Salesman Problems JO - International Journal of Computational Intelligence Systems SP - 692 EP - 705 VL - 11 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.11.1.53 DO - 10.2991/ijcis.11.1.53 ID - Lo2018 ER -
