International Journal of Computational Intelligence Systems

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 10, Issue 1, 2017, Pages 1186 - 1197

A New Efficient Entropy Population-Merging Parallel Model for Evolutionary Algorithms

Authors
Javier Arellano-Verdejo1, *, javier_arellano_verdejo@hotmail.com, Salvador Godoy-Calderon1, sgodoyc@cic.ipn.mx, Federico Alonso-Pecina2, federico.alonso@uaem.mx, Adolfo Guzmán Arenas1, a.guzman@acm.org, Marco Antonio Cruz-Chavez2, mcruz@uaem.mx
*Departament of Computer Sciences and Languages, Universidad de Málaga, Málaga Spain
Corresponding Author
Received 19 October 2016, Accepted 15 August 2017, Available Online 30 August 2017.
DOI
10.2991/ijcis.10.1.78How to use a DOI?
Keywords
Evolutionary Algorithms; Parallel Heuristics; Global Optimization; Parallel Genetic Algorithm; Heuristic Spatially Structured; Island Genetic Algorithm
Abstract

In this paper a coarse-grain execution model for evolutionary algorithms is proposed and used for solving numerical and combinatorial optimization problems. This model does not use migration as the solution dispersion mechanism, in its place a more efficient population-merging mechanism is used that dynamically reduces the population size as well as the total number of parallel evolving populations. Even more relevant is the fact that the proposed model incorporates an entropy measure to determine how to merge the populations such that no valuable information is lost during the evolutionary process. Extensive experimentation, using genetic algorithms over a well-known set of classical problems, shows the proposed model to be faster and more accurate than the traditional one.

Copyright
© 2017, the Authors. Published by Atlantis Press.
Open Access
This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).

1. Introduction

Nowadays several evolutionary algorithms (EAs) have been successfully applied in the solution of many optimization problems, see 1, 2, 3, 4, and 5. Nevertheless, as problems become more and more complex, the execution time of these algorithms increases, making them prohibitively slow for single-core execution. Of course, the population-based nature of evolutionary algorithms, along with the current accelerated development on multi-core hardware technologies, has turned EAs into strong candidates for parallel implementation. Besides the differences in the way each algorithm manages its own heuristic search for optimum values, all EAs share the need to evaluate the fitness of a possibly large population, as well as the need to balance their own mechanisms for global and local search (i.e exploration and exploitation) over the search-space. Thus, several parallel execution models have been proposed for virtually all types of EAs, for example, see 6, 9, 7, and 8

Parallel evolutionary algorithms (PEAs) have been classified into three groups according to their execution model, see 10: master-slave PEAs (Table 1 figure a), coarse-grain PEAs (also known as island-model PEAs) (Table 1 figure b) and fine-grain PEAs (also known as cellular-diffusion PEAs) (Table 1 figure c). Although the master-slave model offers a practical organization and structure for the tasks of the algorithm, it turns to be a terrible waste of the parallel capabilities of the running system. In contrast, the fine-grain model requires too much system capacity and provides no extra mechanisms for controlling the way in which the search space is to be explored and exploited. The island-model appears to be a natural balance between requirements and performance, one that allows leveraging the capabilities of the underlying parallel system and at the same time retain the ability to adjust the exploration/exploitation behavior of the EA.

Table 1.

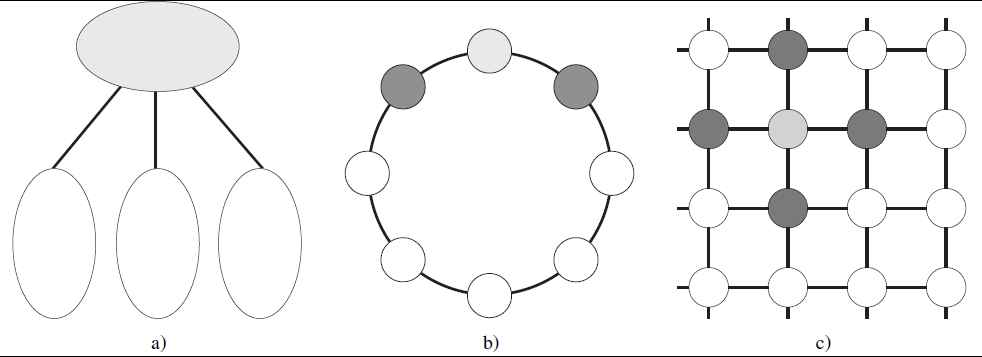
Parallel evolutionary algorithms

In this paper, a new coarse-grain parallel execution model is introduced, which was originally inspired by the traditional island-based model but does not use migration as a solution dispersion mechanism and consequently eliminates the need to select an interconnection topology among islands. In its place a population merging mechanism is used with the option to use several different criteria for selecting island candidates to merge their populations. This option of the model provides by itself an extra control layer that adds to the exploration/exploitation capabilities of the running EA. The rest of this paper is organized as follows: in Section II related works are presented, in Section III, the proposed new model is described, detailing each of the characteristics that make it different and more versatile compared to a traditional migration-based island-model. Section IV shows a set of comparative experiments run with genetic algorithms over the same populations in a migration-based parallel model and in the proposed population-merging model. Finally, in Section V, conclusions are offered.

2. Related works

Every kind of EA requires multiple parameters to function properly. The correct choice for the value of each parameter provides the algorithm with the right balance of exploration and exploitation capabilities. When implemented in parallel, the resulting PEA works as a high level operational layer, thus needing its own set of parameters. It is quite clear that the larger the number of parameters that must be set for the execution of the algorithm, the greater the difficulty to find a right combination of values for them. In fact, the selection of parameters has been posed as an optimization problem itself, with multiple solution proposals as in 11, 12 and 13.

The island model is no exception, as in other evolutionary algorithms, they must to set the parameters values for the mutation and crossing operators however, they must also set a series of additional parameters such as: migration rate (percentage of individuals to be migrated), the migration frequency, interconnection topology (how the islands communicate with one another), the size of the island, etc.14,15.

To reduce the number of parameters that need to be set, T. Hiroyasu et al16 propose an algorithm called DuDGA (Dual Distributed Genetic Algorithm) which defines islands with only two individuals in each of them. After the only two individuals on each island are used for a one-point crossover operation and their descendants are mutated, only the two best fitted individuals (ancestors or descendants) survive for the next generation. Unfortunately, the final result’s quality, as well as the overall performance of this EA, turns out to be very poor as it still depends on a proper choice for the rest the parameters.

In 17, H. Sawai etal. describe an algorithm called PfGA (Parameter free Genetic Algorithm) in which the population size changes as a function of the fitness value of individuals. From every generation, only two parents are selected for multi-point crossover, and there is no need to setup any other parameters. Even traditional genetic algorithm’s parameters like crossover and mutation rates are not needed, since the selection strategy always keeps a small population and a high performance. Although the PfGA itself requires no parameters, the parallel execution layer does and in fact, in 18 it is shown that migration plays an essential role as a tool to improve global search, yet the authors clearly showed that the optimal migration model is different for each problem.

The same type of reduced population (two individuals) is used in 19, where authors introduce an algorithm called VIGA (Variant Island Genetic Algorithm). This algorithm works with a dynamic number of islands and explicit mechanisms called resize, copy and create operations to incrementally take advantage of the convergence status of the search process. Although experimental results show VIGA to be computationally efficient, it relies on global fitness information, which implies high communication overhead when implemented as a distributed parallel algorithm. Also, the fact that a new individual or a mutant is created with low probability means that the parallel execution model dangerously decreases the variance of the population and increases the risk of premature convergence.

Parallel execution models have been proposed for many kinds of EAs other than genetic algorithms. In 20, for example, de la Ossa etal., describe a family of island-based EDAs (Estimation of Distribution Algorithms) and use them to solve numerical optimization problems. The authors select star and ring topologies to experiment with and add a new level of information exchange between islands when using both individual and model migration. Also in 21, the authors propose five types of adaptive parallel PSO algorithms that employed the dynamic exchange of control parameters between multiple swarms-I. The results of this work show that the systems transition appropriately between global and local solution search phases, which means that efficient searches that do not stall at locally optimum solutions are possible.

During the last years, the parallel island model has been successfully used, showing its robustness and applicability in different problems and areas of knowledge such as: Unequal Area Facility22, Job Shop Scheduling23, Cluster Geometry Optimization15, Parallel Harmony Search24, Multi-Objective problems25 and problems of the molecular biology domain26.

Another interesting application is presented in 9, Xin-Yuan Zhang etal. propose a KuhnMunkres parallel genetic algorithm (KMSPGA) to solve the set cover problem, applied to the lifetime maximization of large-scale wireless sensor networks. The proposed algorithm is designed on a divide-and-conquer strategy, and the polynomial KM algorithm is adopted to splice the feasible solutions obtained in each subarea. The KMSPGA schedules the sensors into a number of disjoint complete cover sets and activates them in batch for energy conservation. The results show that it offers promising performance in terms of the convergence rate, solution quality, and success rate.

Also, in the theoretical field several studies have been carried out that have helped for example, to determine the influence of migration by applying discrete-continuous scheduling with continuous resource discretization27. Static and dynamic topologies have been used to determine the best method of interconnection between islands28. Also has been studied different schemes of parallelization and simultaneous use of CPU and GPU that maximize the speedup of these algorithms29. Finally in 30, the island model has been analyzed as a Markov process, which guarantees the asymptotic convergence to the optimum when certain conditions are fulfilled.

The alternative execution model proposed in this paper does not use migration nor a pre-defined connection topology among islands, so the dissemination of the solutions is not dependent on the interconnection topology selected. The migration process has been replaced by a population-merging mechanism between islands, which allows a dynamic way of handling the number of islands as well as the size of the global population. All those tunings and new elements have resulted in a dramatic reduction in the number of times the fitness function is evaluated along the development of the execution, and endows the proposed model with a better control of the way in which the search space is explored and exploited.

3. Merging populations

It is a well-known fact that the quality of the solution found by any EA is directly dependent on the value of its parameters. In addition, the traditional island-model requires the following parameters: number of populations to evolve in parallel (i.e. number of islands), size of the population on each island, interconnection topology and migration policy.

The migration operation in the island model, involves two islands, the origin island O and the destination island D; however, it is possible to select more than one island.

The migration operation is used to modify the diversity of the population of the island D, becoming an important element at the time of the exploration of the search space. The parameters involved in the migration operation are: number of individuals to migrate, frequency of migration, policy for selecting individuals from O, and finally, the policy of replacement in D. The optimal selection of these parameters remains an open problem within parallel models based on islands. However, in 31, the authors performed a large experimental study, where he showed that the optimal amount of individuals to be migrated is approximately 10% of the population every 10 generations (frequency).

The most used selection policy is to take from the island O, those individuals with the best fitness value, they will replace the worst individuals on island D. However, there are other criteria such as those mentioned in 31.

The model proposed in this research, does not make use of migration as a mechanism for preserving diversity in the islands, instead of this, we merge the islands whose entropy value maximizes the diversity of the resulting island population

The Population-Merging Island Model (PMIM) proposed herein slightly modifies the above parameter list and operates on the parameters shown in Table 3. It can be seen that in the PMIM the global population size monotonically decreases over the course of the heuristic search (See figures in Table 2). This is achieved by eliminating all the individuals that were not selected by the fpopulation criterion after the merging process. Consequently, as the global population size decreases, so does the number of times the fitness function is evaluated and, since the total number of islands also decreases, one execution core is freed each round for the parallel system to use for other tasks. In a traditional migration-based island-model both the global population size and the number of islands are kept constant, so the fitness function is evaluated exactly g(ni)k times, where g is the total number of generations the algorithm evolves, ni is the population size of island Ii and k is the total number of islands.

Table 2.

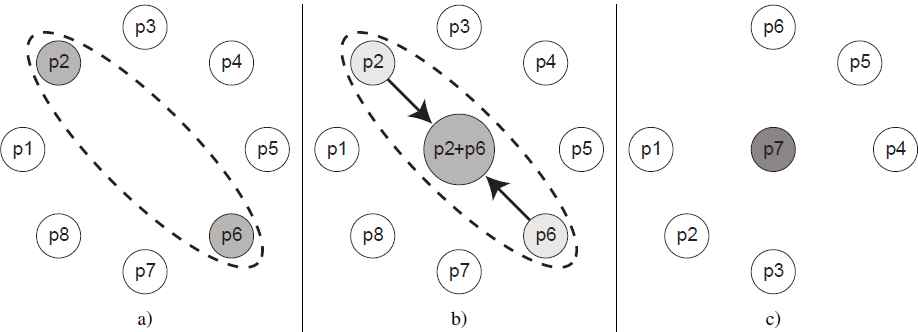
Fusion operation

Parameter Semantics
n Initial size of the population
k Initial number of islands
m Generations to evolve before searching for merging candidates
r Maximum number of evolution/fusion rounds
fisland Island selection criterion for the merger
fpopulation Replacement criteria for merged islands.
Table 3.

PMIM parameters

The use of criterion fisland for selecting islands to be merged eliminates the need to setup interconnection topologies while allowing more freedom in the information exchange mechanism. If the islands selected for merging have a similar fitness variance of their populations then exploitation is promoted, but if islands with notorious population fitness variances are selected, then more exploration is induced into the heuristic search. All of the above happens independently of the EA’s own mechanisms for exploration and exploitation. The PMIM model is specified as shown in Algorithm 1.

(1) 
  P ← GenerateInitialPopulation(n);
(2) 
  I ← CreateIslands(P);
(3) 
  while |I| > 1 do
(4) 
   for all Ii ∈ I in parallel do
(5) 
    Ii ← RunEvolutionaryAlgorithm(Ii);
(6) 
   end for
(7) 
   Iselected ← fisland(I);
(8) 
   I = I − Iselected;
(9) 
   Imerged ← MergeIslands(Iselected);
(10) 
   Imerged ← fpopulation(Imerged);
(11) 
   I ← I ⋃ Imerged;
(12) 
  end while
(13) 
  I ← RunEvolutionaryAlgorithm(I);
(14) 
  best ← getBestIndividual(I);

ALGORITHM PMIM

We have observed, when the population diversity is lost in an evolutionary algorithm, that the population’s entropy is low, which means that the population does not provide important information for the evolutionary process. To select the islands fisland to be merged (See Figure 1), we choose those islands with lowest entropy information, and then after the merging, we preserve the best individuals (see example in Table 2). As can be seen in the results section, the algorithm always converges to the best solution while the number of evaluations to the fitness function decreases monotonically. To calculate the population’s entropy we used the Shannon entropy equation as shown in Equation 1.

H(p)=−∑ip(xi)log2p(xi)

Fig. 1.

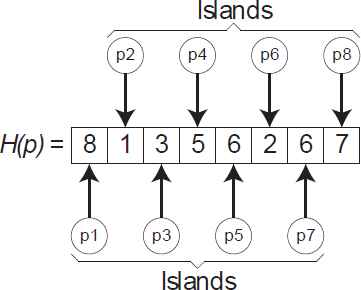
Entropy example for each island

4. Experimental Results

To test the performance of the PMIM the complete benchmark set of ten numerical optimization problems proposed by De Jong and extended by Mezura etal.32 were used. The complete set of functions, along with a specification of their search interval and their known optimum value are shown in Table 4.

Function number Interval Function definition
f1 − 100 ⩽ xi ⩽ 100 ∑i=1500xi2
f2 −10 ⩽ xi ⩽ 10 ∑i=1500|xi|+∏i=1500|xi|
f3 −100 ⩽ xi ⩽ 100 ∑i=1500(∑j=1ixj)2
f4 −100 ⩽ xi ⩽ 100 maxi {|xi|, 1 ⩽ i ⩽ 500}
f5 −30 ⩽ xi ⩽ 30 ∑i=1449|100(xi+1−xi2)2+(xi−1)2|
f6 −100 ⩽ xi ⩽ 100 ∑i=1500(xi+0.5)2
f7 −1.28 ⩽ xi ⩽ 1.28 ∑i=1500ixi4+random[0,1]
f8 −500 ⩽ xi ⩽ 500 ∑i=1500(xisin (xi))
f9 −5.12 ⩽ xi ⩽ 5.12 ∑i=1500[xi2−10cos (2πxi)+10]
f10 −600 ⩽ xi ⩽ 600 14000∑i=1500xi2−∏i=i500cosxii+1
Table 4.

Portfolio of Test Functions

Each problem was solved 100 times by the same parallel genetic algorithm running separately in the traditional island-model and in the PMIM model. Each run generated exactly the same initial population for both models so that results could be fairly compared.

A total of 3000 experiments (10 functions, 100 runs and 3 algorithms), were run on an 8-core Intel Xeon system with 32 GB RAM over a 64 bits Linux operating system. In both models the evolution process for each island is run by a different core.

In the case of the traditional island-model a ring topology, as is the most common case, was used. Migration is accomplished by copying the eight best fitted individuals to other islands according to the selected interconnection topology.

For the PMIM model the fisland criterion was set to randomly select two islands each time and the fpopulation criterion always selected the best fitted two thirds of the individuals from a merged island. The rest of the parameters used for both models are shown in Table 5.

Parameter Island Model PMIM
Size of global population (n) 1000 1000
Size of each island (ni) 125 Dynamical
Generations before migrating/merging 100 100
Migration or fusion rounds (r) 8 8
Number of islands 8 8
fisland ring entropy
fpopulation 8 best → 8 poor ni best fitted
Table 5.

Comparison of parameters used by the two models

From Table 6 it can be seen that the same algorithm, runs faster and gets closer to the global optimum on the PMIM model than on the traditional island-model. Those effects can be attributed to the smaller number of evaluations of the fitness function and the faster dispersion of solutions generated by the population merging process in contrast to the migration process. Table 13 sums up the PMIMs average percentage of improvement observed during the numerical experiments.

Function Fitness of best individual Evaluations of fitness function Execution time
f1 76.00 % 41.20 % 10.91 %
f2 22.66 % 41.33 % 8.86 %
f3 27.22 % 41.27 % 11.67 %
f4 13.88 % 41.12 % 11.18 %
f5 16.60 % 41.17 % 9.95 %
f6 15.30 % 41.29 % 11.55 %
f7 16.25 % 41.47% 11.88 %
f8 9.99 % 41.16 % 9.83 %
f9 27.77 % 41.30 % 14.12 %
f10 23.70 % 41.11% 10.34 %
Table 6.

Improvement of the PMIM over traditional island model

4.1. Statistcal analysis of experimental results

Non-parametric statistical tests have emerged as an effective, affordable, and robust way for evaluating new proposals of metaheuristic and evolutionary algorithms 33. The validation and comparison of new algorithms often requires the definition of a comprehensive experimental framework, including a range of problems and state-of-the-art algorithms. A critical part of these comparisons lies in the statistical validation of the results, contrasting the differences between methods.

To analyze the obtained experimental results, three non-parametric statistical tests have been used. Particularly, the Friedman Classification Test and the Aligned Friedman Test were applied. In addition, the Multi-compare Holm test was used as a post-hoc procedure to find out which algorithms have worse performance than PMIM.

The Friedman Test35 assigns a ri j ranking to the results obtained by each algorithm i, over each data set j. Each ranking is a real number 1 ⩽ ri j ⩽ k , where k is the total number of algorithms to compare. Rankings are assigned in an ascending way, so 1 is the best possible rank, and it gets worse as the assigned rank grows.

As Table 7 shows, the Rj rankings for the PMIM, Island model, and classical Genetic Algorithm algorithms are very similar. This indicates that Island model and Genetic Algorithm have a statistically similar behavior. However, the ranking for the PMIM algorithm shows the lowest value, meaning that considerable differences exist between the performance of PMIM and the other two algorithms.

Algorithm Ranking
PMIM 5.5
Island 20.5
RS 20.5
Table 7.

Average Rankings of the algorithms (Friedman)

The Friedman test is aimed at assessing the performance of the three algorithms over the same dataset, without considering possible relations among all the test datasets. For that reason, when the number of compared algorithms is low, it shows some unusual behavior 35. To avoid this problem, an advanced version of the Friedman test was used, the one designated as the Aligned Friedman Test.

The Aligned Friedman Test 35 estimates the difference between the performance achieved by each algorithm and the localization value. The resulting differences (aligned observations) are ordered in a comparative relative fashion. From that point, the assigned rankings have the same interpretation as in the previous case. The Aligned Friedman Test rankings for each algorithm are presented in Table 8.

Algorithm Ranking
PMIM 5.5
Island 20.5
RS 20.5
Table 8.

Average Rankings of the algorithms (Aligned Friedman)

Again, as can be seen in Table 8, the Aligned Friedman Test clearly shows the existing differences between PMIM and the other algorithms (Aligned Friedman statistic (distributed according to chi-square with 2 degrees of freedom): 7.076228. P-value computed by Aligned Friedman Test: 0.02906810286).

Both, the Friedman test and the Aligned Friedman Test, are limited to detecting differences among the results obtained by each experiment. However, they fail identifying the particular differences between the best ranked algorithm (PMIM) and the other ones. A Holm analysis is then used for comparing each pair of algorithms. The confidence level for each comparison is set to 95% (pvalue = 0.05), which allows to ensure that algorithms are statistically different if they result in pvalue < 0.05. Table 9 shows the resulting pvalue for each set of compared algorithms. When the PMIM algorithm is compared with classical island model or random search, the resulting pvalue is lower than 0.05, therefore refuting the hypothesis that both algorithms have statistically similar behavior.

i algorithm z = (R0 − Ri)/SE p Holm
2 Island 3.810004 0.000139 0.025
1 RS 3.810004 0.000139 0.05
Table 9.

Post Hoc comparison Table for α = 0.05

The null hypothesis, established for the performed post-hoc study, assumes that all three compared algorithms have a statistically similar behavior. The Holm test, with α = 0.05, aims at succeeding in 95% or more of the analyzed results, having a Gaussian (normal) distribution as its point of reference.

Table 9 shows that, when setting PMIM as the reference algorithm, the value obtained for both, the PMIM versus Island case (0.000139), and the PMIM versus GA case (0.000139), is significantly below the α value, so the null hypothesis must be rejected, and consequently, PMIM has a better statistical behavior.

Finally, in order to compare the quality of the solutions between PMIM and others competitors of the state of the art, we have chosen the JADE algorithm and a variant of this as a competitor. JADE was proposed in 34, that algorithm uses a combination between the island model and differential evolution as heuristic to solve problems of numerical optimization.

In Table 10, a comparison of the quality of the solution between PMIM and JADE is shown. An important issue to take into account, is that the PMIM algorithm uses a Genetic Algorithm (GA) with binary encoding as an optimization heuristic, so the representation of the real numbers is limited to the number of bits used by GA.

Function JADE w/o archive JADE with archive PMIM
f1 1.2E48 5.4E67 0.0E+00
f2 1.1E41 9.2E51 0.0E+00
f3 1.2E26 2.2E37 1.7E-08
f4 1.9E02 3.2E71 4.6E-09
f5 5.6E01 4.0E01 3.9E01
f6 1.1E+02 1.2E+02 0.0E+00
f7 1.1E03 7.8E04 6.5E04
f8 8.9E+03 8.6E+03 0.0E+00
f9 1.9E01 2.0E01 0.0E+00
f10 7.9E06 4.2E07 0.0E+00
Table 10.

Quality of the solutions

As it can be seen in Table 10 the quality of the solutions between the algorithms is similar, showing that the reduction in the number of evaluations of fitness function in the PMIM, does not affect the final quality of the solutions.

4.2. Optimal Allocation of Parking Slots

As a second use case, we have used the classic island model as well as the PMIM algorithm, to solve the optimal allocation of parking spots proposed in 36. To carry out the comparison of the results, we used the same set of data of the original work.

In a simple sentence, the problem of optimal allocation of parking slots can be understood as follows: on the one hand, a set of drivers and their preferences about a desired parking place, and on the other hand a set of public parking slots; the goal is to optimally allocate the best parking slot for each driver minimizing some given cost function. In order to solve the optimal allocation of parking spots problem, it is necessary to have, on the one hand, a model of the city and, on the other hand, a simulation of this city.

The fitness function for this problem is shown in Equation 2 (minimization problem). It is composed of two parts: F1 and F2. To calculate F1, for all cars encoded in the individual, we perform the accumulated sum of the cost δ for the shortest paths between the node where the car is at the time of the request, named sp, and the node to which the assigned slot belongs ap, as well as the cost between the node to which the desired slot ds belongs and the assigned slot. For each position i, j of the δ matrix, the shortest path between nodes i and j is calculated by using Dijkstra’s algorithm.

F=αF1(x)+βF2(x)
F1(x)=∑i=1nδ(spi,api)+δ(api,dpi)

Table 11 shows the parameters used for the comparison of the algorithms. As it can be seen in Table 12, again the PMIM algorithm has reduced the number of evaluations of the fitness function in more than 30%.

Parameter Island Model PMIM
Size of global population (n) 100 100
Size of each island (ni) 10 Dynamical
Generations before migrating/merging 1000 1000
Migration or fusion rounds (r) 10 10
Number of islands 10 10
fisland ring entropy
fpopulation 8 best → 8 poor ni best fitted
Table 11.

Comparison of parameters used by the two models

Instance Improvement
1 34.5 %
2 31.7 %
3 30.3 %
4 32.7 %
5 33.5 %
6 34.8 %
7 32.9 %
8 30.1 %
9 32.8 %
Table 12.

Improvement of the PMIM

5. Conclusions

A new coarse-grain (parallel) execution model for evolutionary algorithms was presented. The new model, called Population Merging Island Model (PMIM) replaces migration with a population merging system as the solution dispersion mechanism used by the traditional island-model. In doing so, the PMIM model eliminates the need for choosing an interconnection topology among islands, which is one of the parameters with the greatest impact on the accuracy and performance of the evolutionary algorithm.

When the population of two or more islands is merged and then reduced, the global population size decreases, as well as the number of evolving islands. The immediate effect of this is a reduction in the number of evaluations of the fitness function with the consequent decrease in execution time. Also the PMIM model offers an extra layer to help on the exploration and exploitation control capabilities of the heuristic search which results in a higher precision on the quality of the found solution.

Extensive numerical experimentation, using the benchmark function suite proposed by De Joung and a GA as the inner EA shows the PMIM model to be faster and more precise than the traditional island-model (see Table 13).

Fitness Number of evaluations Execution time
7.6% 41.24% 10.81%
Table 13.

Average improvement of the PMIM

6. Future work

  • •

    As part of our future work, we are working on a new mechanism to select an effective local search method based in the evolution of different search trajectory algorithms (different to hyperheuristics). The goal is to employ the best algorithms for the subpopulation’s landscape that we want to define.

  • •

    Also, we think that it is important to design a mechanism to split some populations when their entropy is high, in order to improve the exploration procedure of the algorithm.

  • •

    Test the algorithm with combinatorial problems and problems with constraints.

Acknowledgments

  • •

    We thank to the Programa para el Desarrollo Profesional Docente (PRODEP) for provide a posdoctoral scholarship

  • •

    “CONACyT, Consejo Nacional de Ciencia y Tecnología de México” for its economical support in the program “Estancias Posdoctorales Internacionales 2015-2016” for the project with registration number 263564

References

1.XN Shen, L Minku, R Bahsoon, and X Yao, Dynamic Software Project Scheduling through a Proactive-rescheduling Method, IEEE Trans. Softw. Eng, Vol. 42, No. 7, 2016, pp. 658-686. doi: http://dx.doi.org//10.1109/TSE.2015.2512266
2.CH Chen and JH Chou, Evolutionary Design of Adjustable Six-Linkage Bar Manufacturing Mechanisms Using Niche Genetic Algorithms, IEEE Access, Vol. 4, 2016, pp. 4809-4822. doi: http://dx.doi.org//10.1109/ACCESS.2016.2597869
3.JK Byun, I Volvach, and V Lomakin, Fast Optimal Design of Micromagnetic Devices Using FastMag and Distributed Evolutionary Algorithm, IEEE Trans. Magn, Vol. 52, No. 9, 2016. doi: http://dx.doi.org//10.1109/TMAG.2016.2562600
4.F Susanto, S Budi, P de Souza, U Engelke, and J He, Design of Environmental Sensor Networks Using Evolutionary Algorithms, IEEE Geosci. Remote Sens. Lett, Vol. 4, No. 13, 2016, pp. 575-579. doi: http://dx.doi.org//10.1109/LGRS.2016.2525980
5.J Arellano-Verdejo, E Alba, and S Godoy-Calderon, Efficiently finding the optimum number of clusters in a dataset with a new hybrid differential evolution algorithm: DELA, Soft Comput, Vol. 20, No. 3, 2016, pp. 895-905. doi: http://dx.doi.org//10.1007/s00500-014-1548-6
6.YJ Gong, JJ Li, Y Zhou, Y Li, HSH Chung, YH Shi, and J Zhang, Genetic learning particle swarm optimization, IEEE Trans. Cybernetics, Vol. 10, No. 46, 2015, pp. 2277-2290. doi: http://dx.doi.org//10.1109/TCYB.2015.2475174
7.J Yi, D Huang, S Fu, H He, and T Li, Multi-Objective Bacterial Foraging Optimization Algorithm Based on Parallel Cell Entropy for Aluminum Electrolysis Production Process, IEEE Trans Ind. Electron, Vol. 4, No. 63, 2016, pp. 2488-2500. doi: http://dx.doi.org//10.1109/TIE.2015.2510977
8.R Datta, S Pradhan, and B Bhattacharya, Analysis and Design Optimization of a Robotic Gripper Using Multiobjective Genetic Algorithm, IEEE T SYST MAN CY B Transactions on Systems, Man, and Cybernetics: Systems, Vol. 1, No. 46, 2016, pp. 16-26. doi: http://dx.doi.org//10.1109/TSMC.2015.2437847
9.XY Zhang, YJ Gong, Z Zhan, WN Chen, Y Li, and J Zhang, Kuhn-Munkres Parallel Genetic Algorithm for the Set Cover Problem and Its Application to Large-Scale Wireless Sensor Networks, IEEE T EVOLUT COMPUT, 2015. doi: http://dx.doi.org//10.1109/TEVC.2015.2511142
10.E Alba, Parallel metaheuristics: a new class of algorithms, John Wiley & Sons, Vol. 47, 2005. http://dx.doi.org/10.1002/0471739383
11.H Seada and K Deb, A Unified Evolutionary Optimization Procedure for Single, Multiple, and Many Objectives, IEEE T EVOLUT COMPUT, Vol. 3, No. 20, 2016, pp. 358-369. doi: http://dx.doi.org//10.1109/TEVC.2015.2459718
12.H Xie and M Zhang, Parent Selection Pressure Auto-Tuning for Tournament Selection in Genetic Programming, IEEE T EVOLUT COMPUT, Vol. 1, No. 17, 2013, pp. 1-19. doi: http://dx.doi.org//10.1109/TEVC.2011.2182652
13.PK Lehre and X Yao, On the Impact of Mutation-Selection Balance on the Runtime of Evolutionary Algorithms, IEEE T EVOLUT COMPUT, Vol. 2, No. 16, 2012, pp. 225-241. doi: http://dx.doi.org//10.1109/TEVC.2011.2112665
14.ZM Skolicki, An Analysis of Island Models in Evolutionary Computation, George Mason University, 2007. Doctoral dissertation, http://dx.doi.org/10.1145/1102256.1102343
15.A Leitão, F Baptista-Pereira, and P Machado, Island models for cluster geometry optimization: how design options impact effectiveness and diversity, J Glob Optim, Vol. 63, 2015, pp. 677-707. doi: http://dx.doi.org/10.1007/s10898-015-0302-7
16.T Hiroyasu, M Miki, T Iwahashi, and Y Okamoto, Dual individual distributed genetic algorithm for minimizing the energy of protein tertiary structure, IEEE, in SICE 2003 Annual Conference (2003, August), Vol. 3, pp. 2756-2761.
17.H Sawai and S Kizu, Parameter-free genetic algorithm inspired by ”disparity theory of evolution”, Springer, in International Conference on Parallel Problem Solving from Nature (Berlin Heidelberg, 1998, September), pp. 702-711. doi: http://dx.doi.org//10.1007/BFb0056912
18.S Adachi and H Sawai, Effects of migration methods in parallel distributed parameter free genetic algorithm, ELECTR COMMUN JPN, Vol. 85, No. 11, 2002, pp. 71-80. (Part II: Electronics) doi: http://dx.doi.org//10.1002/ecjb.10096
19.T Jumonji, G Chakraborty, H Mabuchi, and M Matsuhara, A novel distributed genetic algorithm implementation with variable number of islands, IEEE, in 2007 IEEE Congress on Evolutionary Computation (2007, September), pp. 4698-4705. doi: http://dx.doi.org//10.1109/CEC.2007.4425088
20.JA Gámez and JM Puerta, Initial approaches to the application of islands-based parallel EDAs in continuous domains, J PARALLEL DISTR COM, Vol. 66, No. 8, 2006, pp. 991-1001. doi: http://dx.doi.org//10.1016/j.jpdc.2006.03.005
21.M Suzuki, Adaptive Parallel Particle Swarm Optimization Algorithm Based on Dynamic Exchange of Control Parameters, American Journal of Operations Research, Vol. 6, No. 5, 2016, pp. 401. doi: http://dx.doi.org/10.4236/ajor.2016.65037
22.JM Palomo-Romero, L Salas-Morera, and L García-Hernández, An island model genetic algorithm for unequal area facility layout problems, Expert Syst. Appl, Vol. 68, 2017, pp. 151-162. doi: http://dx.doi.org/10.1016/j.eswa.2016.10.004
23.M Kurdi, An effective new island model genetic algorithm for job shop scheduling problem, Comput. Oper. Res, Vol. 67, 2016, pp. 132-142. doi: http://dx.doi.org/10.1016/j.cor.2015.10.005
24.MA Al-Betar, MA Awadallah, AT Khader, and ZA Abdalkareem, Island-based harmony search for optimization problems, Expert Syst. Appl, Vol. 42, 2015, pp. 2026-2035. doi: http://dx.doi.org/10.1016/j.eswa.2014.10.008
25.H Rajabalipour-Cheshmehgaz, M Ishak-Desa, and A Wibowo, Effective local evolutionary searches distributed on an island model solving bi-objective optimization problems, Appl Intell, Vol. 38, 2013, pp. 331-356. doi: http://dx.doi.org/10.1007/s10489-012-0375-7
26.K Tamura, H Kitakami, and A Nakada, Distributed Modified Extremal Optimization using Island Model for Reducing Crossovers in Reconciliation Graph, Engineering Letters, Vol. 21, No. 2, 2013, pp. 81-88.
27.P Jdrzejowicz and A Skakovski, Properties of the Island-Based and Single Population Differential Evolution Algorithms Applied to Discrete-Continuous Scheduling, in Proceedings of the 8th KES International Conference on Intelligent Decision Technologies (2016), pp. 349-359. doi: http://dx.doi.org/10.1007/978-3-319-39630-9_29
28.R Ayala-Lopes, RC Pedrosa Silva, ARR Freitas, F Campelo, and FG Guimares, Study on the Configuration of Migratory Flows in Island Model Differential Evolution, in In GECCO’14 (July 12-16, (2014)), pp. 1015-102. doi: http://dx.doi.org/10.1145/2598394.2605439
29.S Limmer and D Fey, Comparison of common parallel architectures for the execution of the island model and the global parallelization of evolutionary algorithms, Concurrency Computat.: Pract. Exper, Vol. 29, 2017, pp. e3797. doi: http://dx.doi.org 10.1002/cpe.3797
30.R Schaefer, A Byrski, and M Smolka, The island model as a markov dynamic system, Int. J. Appl. Math. Comput. Sci, Vol. 22, No. 4, 2012, pp. 971-984. doi: http://dx.doi.org/10.2478/v10006-012-0072-z
31.M Tomassini, Spatially structured evolutionary algorithms: artificial evolution in space and time, Springer Science & Business Media, 2006. http://dx.doi.org/10.1007/3-540-29938-6
32.E Mezura-Montes, J Velázquez-Reyes, and CA Coello Coello, A comparative study of differential evolution variants for global optimization, in Proceedings of the 8th annual conference on Genetic and evolutionary computation (2006, July), pp. 485-492. ACM http://dx.doi.org/10.1145/1143997.1144086
33.S García, D Molina, M Lozano, and F Herrera, A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: a case study on the CEC’2005 special session on real parameter optimization, J. Heuristics, Vol. 15, No. 6, 2009, pp. 617-644. http://dx.doi.org/10.1007/s10732-008-9080-4
34.J Zhang and AC Sanderson, JADE: adaptive differential evolution with optional external archive, IEEE Transactions on evolutionary computation, Vol. 13, No. 5, 2009, pp. 945-958. http://dx.doi.org/10.1109/tevc.2009.2014613
35.M Cortina-Borja, Handbook of parametric and non-parametric statistical procedures, 2012.
36.J Arellano-Verdejo and E Alba, Optimal Allocation of Public Parking Slots Using Evolutionary Algorithms, IEEE, in Intelligent Networking and Collaborative Systems (INCoS), 2016 International Conference on (2016, September), pp. 222-228. http://dx.doi.org/10.1109/incos.2016.21
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
International Journal of Computational Intelligence Systems
Volume-Issue
10 - 1
Pages
1186 - 1197
Publication Date
2017/08/30
ISSN (Online)
1875-6883
ISSN (Print)
1875-6891
DOI
10.2991/ijcis.10.1.78How to use a DOI?
Copyright
© 2017, the Authors. Published by Atlantis Press.
Open Access
This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Javier Arellano-Verdejo
AU  - Salvador Godoy-Calderon
AU  - Federico Alonso-Pecina
AU  - Adolfo Guzmán Arenas
AU  - Marco Antonio Cruz-Chavez
PY  - 2017
DA  - 2017/08/30
TI  - A New Efficient Entropy Population-Merging Parallel Model for Evolutionary Algorithms
JO  - International Journal of Computational Intelligence Systems
SP  - 1186
EP  - 1197
VL  - 10
IS  - 1
SN  - 1875-6883
UR  - https://doi.org/10.2991/ijcis.10.1.78
DO  - 10.2991/ijcis.10.1.78
ID  - Arellano-Verdejo2017
ER  -