A Comprehensive Literature Review of 50 Years of Fuzzy Set Theory
- DOI
- 10.1080/18756891.2016.1180817How to use a DOI?
- Keywords
- Fuzzy Set Theory; Intuitionistic Fuzzy Sets; Hesitant Fuzzy Sets; Type N Fuzzy Sets; Multi Fuzzy Sets; Nonstationary fuzzy sets
- Abstract
Fuzzy sets have a great progress in every scientific research area. It found many application areas in both theoretical and practical studies from engineering area to arts and humanities, from computer science to health sciences, and from life sciences to physical sciences. In this paper, a comprehensive literature review on the fuzzy set theory is realized. In the recent years, ordinary fuzzy sets have been extended to new types and these extensions have been used in many areas such as energy, medicine, material, economics and pharmacology sciences. This literature review also analyzes the chronological development of these extensions. In the last section of the paper, we present our interpretations on the future of fuzzy sets.
- Copyright
- © 2016. the authors. Co-published by Atlantis Press and Taylor & Francis
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
A fuzzy set is a class of objects whose memberships are not precisely defined [1]. Fuzzy sets provide a better representation of reality than the classical mathematical binary representation. The membership in fuzzy sets is gradual, that makes the theory invaluable to represent the limited level of precision in mental representations [2].
The founder of the fuzzy set theory Lotfi Asker Zadeh published his first paper on his new theory in 1965. Between 1965 and 1975, Zadeh broadened the foundation of the fuzzy set theory by establishing fuzzy similarity relations, linguistic hedges, and fuzzy decision-making. In 1970s, some research groups in Japan started to study the fuzzy set theory. In 1970, Mamdani developed the first fuzzy logic controller. In 1977, some industrial applications of fuzzy logic began in Japan and Europe. The success of fuzzy logic was observed in Japan at the beginning of 1980s and this led to a revival in fuzzy logic in the US at the end of 1980s. Along with the emergence of the fuzzy set theory, many objections to the theory have appeared [3]. Those brilliant scientists could not accept Zadeh’s way of handling the uncertainty. They so much exaggerated in decrying it that the logic of the theory was defined as “Fuzzy logic is the cocaine of science.” However, the fuzzy logic proved its power through the real technology applications.
One of the well-known applications of fuzzy logic is that of the Sendai Subway system that went into operation in 1988 in Sendai, Japan. For the control of lines, a fuzzy controller was used to run the train all day long. Through the fuzzy controller, the line became one of the smoothest running subway systems in the world. The commercial appliances such as heating ventilation and air conditioning (HVAC) systems have used fuzzy logic thermostats to control the heating and cooling thus saved energy by making the system more efficient and keeping the temperature more steady than a traditional thermostat. Fuzzy logic control systems have also been used to control the speed of cars based on the obstacle sensed. The system is composed of a sensor in the front panel to sense the presence of obstacles. Fuzzy logic based Programmable Logic Controllers (PLCs) have been developed by companies like Moeller, one of the longest-established and most respected names in the electrical sector. Fuzzy logic has also been used in 3D animation systems for generating crowds as it was used extensively in the making of the Lord of the Rings.
In this paper, a comprehensive literature review for the fuzzy set theory is realized. It aims at exhibiting the expansion areas of the fuzzy set theory in its 50th year and presents the results of literature review with graphical illustrations and a classification with respect to the extensions of fuzzy sets. It is the most comprehensive and up to date literature review of the fuzzy set theory.
The rest of the paper is organized as follows. In Section 2, some graphical illustrations on the most productive authors writing fuzzy papers and their affiliations; frequencies, sources, and countries of these papers are presented. Section 3 includes the subject areas of fuzzy papers and some related statistics. Section 4 gives the classification of extensions of fuzzy sets including the important works on these sets. Section 5 presents the expectations of the authors about the future of the fuzzy set theory. Section 6 finally concludes the paper.
2. Fuzzy Set Theory with Graphical Illustrations
In this section, the whole publications including the word fuzzy in their titles are classified with respect to their publication years, publication sources, authors, the affiliations of authors, the countries of the authors, document types and subject areas. Each classification type is enhanced by the graphical and tabular illustrations. The search was made in October 12, 2015 based on Scopus database.
The overall picture is illustrated by Figures 1–7 and Tables 1–2. Figure 1 illustrates the frequencies of the papers using the fuzzy set theory with respect to years.
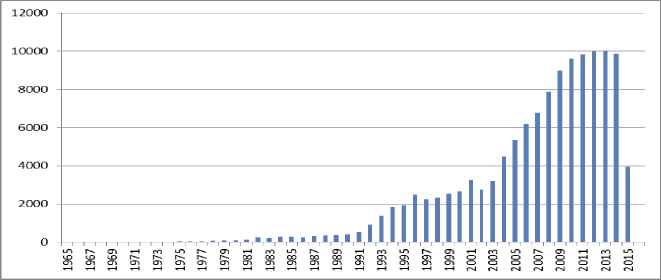
Frequencies of fuzzy papers with respect to years
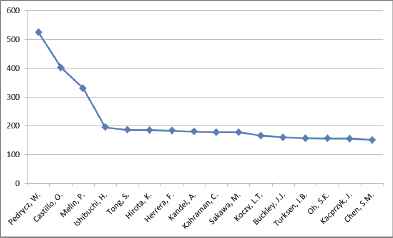
The authors publishing fuzzy papers over 150
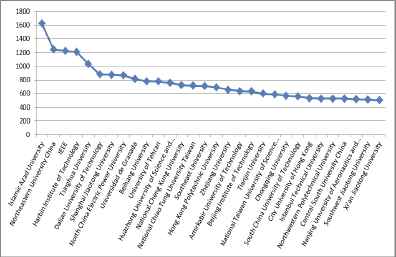
The affiliations publishing more than 500 fuzzy papers
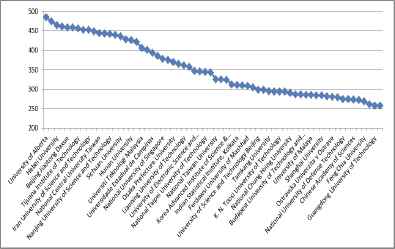
The affiliations publishing between 250 and 500 fuzzy papers
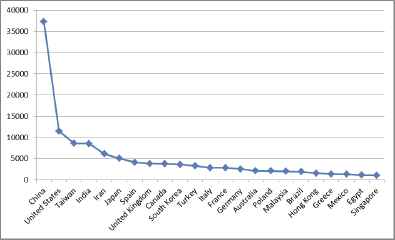
Countries publishing fuzzy papers more than 1000
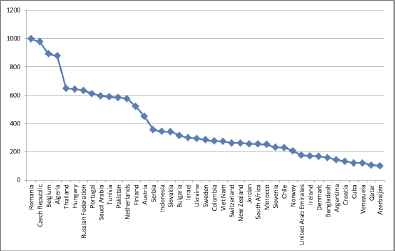
Countries publishing fuzzy papers between 100 and 1000
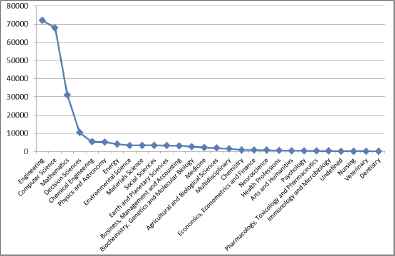
Subject areas of the published fuzzy papers and the frequencies
| Sources | Frequency |
|---|---|
| Fuzzy Sets and Systems | 5376 |
| IEEE International Conference on Fuzzy Systems | 4656 |
| Lecture Notes in Computer Science Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics | 3655 |
| Applied Mechanics and Materials | 1484 |
| IEEE Transactions on Fuzzy Systems | 1438 |
| Expert Systems with Applications | 1348 |
| Information Sciences | 1343 |
| Advanced Materials Research | 1258 |
| Annual Conference of the North American Fuzzy Information Processing Society NAFIPS | 1228 |
| Proceedings of SPIE the International Society for Optical Engineering | 967 |
| Journal of Intelligent and Fuzzy Systems | 855 |
| Proceedings of the World Congress on Intelligent Control and Automation WCICA | 843 |
| Studies in Fuzziness and Soft Computing | 783 |
| Proceedings of the IEEE International Conference on Systems Man and Cybernetics | 724 |
| Applied Soft Computing Journal | 719 |
| Communications in Computer and Information Science | 626 |
| Soft Computing | 535 |
| IECON Proceedings Industrial Electronics Conference | 478 |
| Studies in Computational Intelligence | 475 |
| IEEE Transactions on Systems Man and Cybernetics Part B Cybernetics | 466 |
| Advances in Intelligent Systems and Computing | 463 |
| IFAC Proceedings Volumes IFAC Papersonline | 456 |
| Kongzhi Yu Juece Control and Decision | 445 |
| International Journal of Uncertainty Fuzziness and Knowledge Based Systems | 439 |
| Lecture Notes in Artificial Intelligence Subseries of Lecture Notes in Computer Science | 428 |
| Proceedings of the American Control Conference | 407 |
| Advances in Soft Computing | 398 |
| Lecture Notes in Electrical Engineering | 395 |
| International Journal of Intelligent Systems | 389 |
| International Journal of Approximate Reasoning | 376 |
| European Journal of Operational Research | 368 |
| Xitong Fangzhen Xuebao Journal of System Simulation | 368 |
| Proceedings of the International Joint Conference on Neural Networks | 361 |
| Computers and Mathematics with Applications | 361 |
| Neurocomputing | 358 |
| Advances in Intelligent and Soft Computing | 352 |
| International Journal of Fuzzy Systems | 349 |
| International Journal of Innovative Computing Information and Control | 349 |
| Kongzhi Lilun Yu Yingyong Control Theory and Applications | 339 |
| Engineering Applications of Artificial Intelligence | 336 |
| Proceedings of the IEEE Conference on Decision and Control | 316 |
| Xi Tong Gong Cheng Yu Dian Zi Ji Shu Systems Engineering and Electronics | 311 |
| Iranian Journal of Fuzzy Systems | 299 |
| International Journal of Advanced Manufacturing Technology | 297 |
| Mathematical Problems in Engineering | 295 |
| Neural Computing and Applications | 276 |
| International Journal of Systems Science | 262 |
| IEEE International Conference on Neural Networks Conference Proceedings | 258 |
| Computers and Industrial Engineering | 254 |
| Journal of Mathematical Analysis and Applications | 242 |
The sources publishing fuzzy papers
It indicates that there is an increasing trend starting at the beginning of 1990s. After 2002, the numbers of published papers using the fuzzy set theory have almost an arithmetic increase. The number of these papers reaches to a saddle point of 10,000 papers per year.
Table 1 shows the sources publishing fuzzy papers and the number of fuzzy papers published up to now. According to this table, “Fuzzy Sets and Systems” and “IEEE International Conference on Fuzzy Systems” are the sources that most publishing fuzzy papers.
Figure 2 shows the authors publishing over 150 papers up to now, based on the fuzzy set theory. W. Pedrycz, O. Castillo, and P. Melin are the most productive authors in this field.
Figure 3 shows the affiliations publishing more than 500 fuzzy papers up to now whereas Figure 4 presents the same for between 250–500 fuzzy papers. Islamic Azad University in Iran takes the first rank publishing papers using the fuzzy set theory. There are 7 universities from China in the first 10 ranks. IEEE and Granada University are the other two affiliations in the first 10 ranks.
Figure 5 shows the countries publishing fuzzy papers more than 1000 up to now. China, United States, Taiwan, India and Iran are the first 5 leading countries. Figure 6 illustrates the same for between 100–1000 fuzzy papers.
Table 2 shows the classification of fuzzy publications. Most of the documents are articles and conference papers.
| Document type | Frequency |
|---|---|
| Article | 64,955 |
| Conference Paper | 56,915 |
| Review | 848 |
| Article in Press | 846 |
| Book Chapter | 524 |
| Erratum | 248 |
| Conference Review | 220 |
| Editorial | 218 |
| Note | 164 |
| Book | 117 |
| Letter | 97 |
| Short Survey | 27 |
| Report | 12 |
Classification of fuzzy publications
Figure 7 illustrates the subject areas of the published fuzzy papers and their frequencies. The fuzzy papers are mostly used in engineering and computer science areas.
3. Subject Areas of Fuzzy Publications
In this section, we analyze the subject areas of the papers using the fuzzy set theory. These areas are engineering, computer science, mathematics, decision sciences, life sciences, physical sciences, and health sciences.
3.1. Engineering
The number of papers using the fuzzy sets on engineering is 71,928. There are 355 fuzzy sets based patents, received on engineering. Figure 8 illustrates the distribution of papers using the fuzzy set theory on engineering area with respect to years.
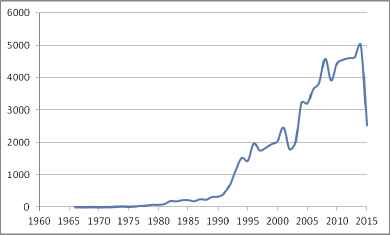
Distribution of fuzzy papers on engineering area with respect to years
A significant trend in fuzzy engineering publications begins in 1992 even some fluctuations are observed.
3.2. Computer Science
The number of papers using the fuzzy sets on computer science is 67,898. There are 1,241 fuzzy sets based patents, received on computer science. Figure 9 shows the distribution of papers using the fuzzy set theory on computer science area with respect to years.
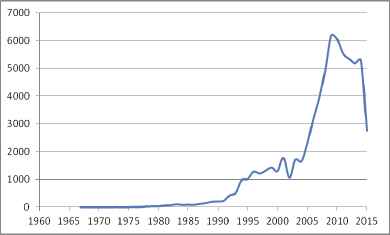
Distribution of fuzzy papers on computer science area with respect to years
A significant trend in fuzzy computer science publications begins in 1992 even some fluctuations are observed.
3.3. Mathematics
The number of papers using the fuzzy sets on mathematics is 31,073. There are 855 fuzzy sets based patents, received on mathematics. Figure 10 illustrates the distribution of papers using the fuzzy set theory on mathematics area with respect to years.
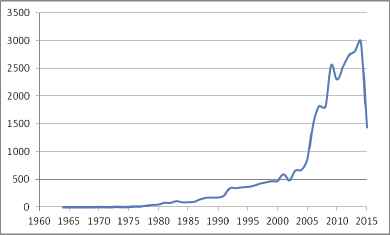
Distribution of fuzzy papers on mathematics area with respect to years
An increasing trend in fuzzy mathematics publications begins in 1980s but the significant trend begins at the beginning of 2000s even some fluctuations are observed.
3.4. Decision Sciences
The number of papers using the fuzzy sets on decision sciences is 10,273. There are 6 fuzzy sets based patents, received on decision sciences. Figure 11 illustrates the distribution of papers using the fuzzy set theory on decision sciences area with respect to years.
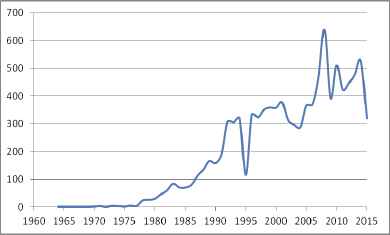
Distribution of fuzzy papers on decision sciences area with respect to years
An increasing trend in fuzzy decision sciences publications begins in 1980s but the significant trend begins at the beginning of 1990s even some fluctuations are observed. It is noticeable that a sudden falling down in 1995 and a sudden rising up in 2008 occur.
3.5. Life Sciences
The life sciences are composed of the fields of science that involve the scientific study of living organisms such as microorganisms, plants, animals, and human beings. The fuzzy set theory has been used 2,598 times in the papers on biochemistry, genetics and molecular biology while it is used 1,833 times on agricultural and biological sciences, 139 times on immunology and microbiology, and 28 times on veterinary.
3.6. Physical Sciences
Physical sciences are composed of the fields of science that involve the scientific study of non-living systems. The fuzzy set theory has been used 5,166 times in the papers on physics and astronomy while it is used 3,248 times on materials science.
3.7. Health Sciences
Health sciences are applied sciences that address the use of science, technology, engineering or mathematics in the delivery of healthcare. The fuzzy set theory has been used 189 times in Pharmacology, Toxicology and Pharmaceutics; 51 times in nursing; 8 times in dentistry; 249 times in psychology; and 386 times in health professions.
3.8. Social Sciences and Humanities
Social science is a major category of academic disciplines, concerned with society and the relationships among individuals within a society. The humanities and social sciences are the study of human behavior and interaction in social, cultural, environmental, economic and political contexts. These sciences provide a set of skills including business, communication, education, law, medicine, politics, and psychology, etc. The fuzzy set theory has been used 3,244 times in social sciences.
4. Fuzzy sets and their extensions
Fuzzy sets have a history starting from ordinary fuzzy sets and extending to other types of fuzzy sets as illustrated in Figure 12.
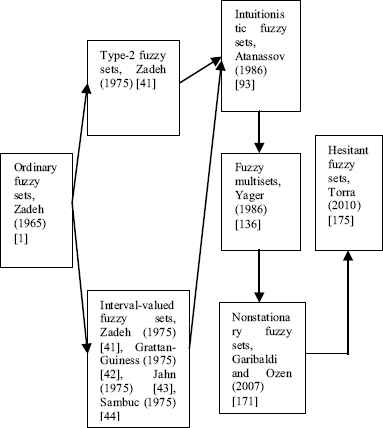
Extensions of fuzzy sets
In the following, the historical progresses of ordinary fuzzy sets and its following extensions are given.
4.1. Ordinary fuzzy sets
If X is a collection of objects denoted generically by x, then a fuzzy set à in X is a set of ordered pairs:
Zadeh [1] introduced fuzzy sets as a class of objects with a continuum of grades of membership. He extended the notions of inclusion, union, intersection, complement, relation, convexity, etc. to such sets, and established various properties of these notions in the context of fuzzy sets. Zadeh [4] suggested linguistic hedges as operators which act on the fuzzy set representing the meaning of its operand. De Luca and Termini [5] introduced a function defined on the class of generalized characteristic functions using no probabilistic concepts in order to obtain a global measure of the indefiniteness described by fuzzy sets. Bezdek [6] utilized a fuzzy clustering technique to analyze the substructure of a well-known set of 4-dimensional botanical data.
Zadeh [7] proposed that the imprecision that is intrinsic in natural languages is possibilistic rather than probabilistic in nature and a proposition in a natural language may be translated into a procedure which computes the probability distribution of a set of attributes which are implied by that proposition by employing the concept of a possibility distribution. Baldwin and Guild [8] reviewed some methods of making fuzzy decisions, which include a comparison of fuzzy sets on the same space and described a new approach which overcomes their drawbacks. Lowen [9] gathered some elementary known results about convex fuzzy sets and introduced the necessary concepts. Alsina et al. [10] proposed some logical connectives for the fuzzy set theory. Dubois and Prade [11] provided an extensive survey on fuzzy set-theoretic operations, and emphasized the relevance of the theory of functional equations in the axiomatical construction of classes of such operations and the derivation of functional representations. Dubois and Prade [12] proposed various formal settings, including but not restricted to fuzzy sets and possibility measures, based on different intuitions, and dealing with various kinds of uncertain data.
Yen [13] described a generalization of the D-S theory and showed that computing the degree of belief in a hypothesis in the D-S theory can be formulated as an optimization problem. Diamond and Kloeden [14] introduced two classes of metrics for spaces of fuzzy sets. Their equivalence is discussed and basic properties established. Dubois and Prade [15] proposed the possibility theory. They emphasized simple basic ideas that govern most of the existing methods, especially the principles of minimum specificity and the combination/projection principle that facilitate a comparison between fuzzy set-based methods and other numerical approaches to automated reasoning. Yager [16] discussed some of the issues involved in the selection of appropriate operators for implementing the union and intersection of fuzzy subsets. He discussed the extension principles used in extending operators to fuzzy subsets and provided a structure for aggregating linguistic variables in the theory of approximate reasoning. Xuecheng [17] gave the axiom definitions of entropy, distance measure and similarity measure of fuzzy sets systematically and discussed basic relations between these measures. Lee-Kwang et al. [18] proposed two similarity measures: one for the similarity between fuzzy sets and the other between elements in fuzzy sets.
Dubois and Prade [19] advocated the claim that progress in operational semantics of membership functions presupposes that these distinct semantics be acknowledged and related to more basic measurement issues in terms of distance, cost and frequency, on which scientific traditions exist. Wang [20] proposed two new similarity measures to represent the similarity measure between fuzzy sets and between elements. Yao [21] reviewed and compared theories of fuzzy sets and rough sets. They reviewed two approaches for the formulation of fuzzy sets, one is based on many-valued logic and the other is based on modal logic. Zadeh [22] described the theory of possibility, which is related to the theory of fuzzy sets by defining the concept of a possibility distribution as a fuzzy restriction which acts as an elastic constraint on the values that may be assigned to a variable. Pedrycz [23] introduced a concept of fuzzy equalization which concerns a process of building information granules that are semantically and experimentally meaningful. Dubois et al. [24] proved that a leximin-optimal solution to a vector ranking problem on the unit hypercube can be obtained as the limit of optimal solutions to a problem of fuzzy multiple criteria optimization.
Pedrycz and Vukovich [25] generalized an issue of feature selection by introducing a mechanism of fuzzy feature selection. Mendel [26] presented a new theory of fuzzy sets for words that is based on collecting data from people that reflect intra- and inter-levels of uncertainties about a word. Deschrijver and Kerre [27] introduced the notion of uninorm in interval-valued fuzzy set theory, or equivalently in intuitionistic fuzzy set theory. Dubois et al. [28] described new properties of a transformation of a probability distribution into a possibility distribution, by relating it with the well-known probability inequalities of Bienaymé-Chebychev and Camp-Meidel. Trillas [29] tried to stimulate some reflections in order to extend the current theories of fuzzy sets to wider areas of both language and reasoning.
Montero et al. [30] stressed the relevance of a particular family of fuzzy sets, where each element can be viewed as the result of a classification problem. Dubois and Prade [31] introduced a new concept in the fuzzy set theory, that of a gradual element. They outlined applications of this notion to fuzzy cardinality, fuzzy interval analysis, fuzzy optimization, and defuzzification principles. Dubois and Prade [32] studied the algebraic structure of bodies of evidence on a set, based on extended set union, intersection and complementation.
Pedrycz [33] dealt with a category of logic operators for fuzzy sets that is inherently associated with underlying statistical properties of membership grades they operate on. Liu et al. [34] redefined the concept of fuzzy rough sets and studied it in the setting of the Axiomatic Fuzzy Set theory. Pedrycz [35] concentrated on the architectures and fundamentals supporting the reconciliation and characterization of a family of fuzzy models aimed at the representation of the same system from different cognitive perspectives.
García-Honrado and Trillas [36] showed that the membership function of a fuzzy set exhibits some intrinsic property related with how this fuzzy set is actually managed in the universe of discourse. Kerre [37] outlined the shortcomings of classical binary logic and Cantor’s set theory in order to handle imprecise and uncertain information and introduced the basic notions of Zadeh’s fuzzy set theory among them. Dubois and Prade [38] discussed basic notions underlying fuzzy sets, especially gradualness, uncertainty, vagueness and bipolarity, in order to clarify the significance of using fuzzy sets in practice. Pedrycz [39] introduced a concept of a granular representation of numeric membership functions of fuzzy sets, which offers a synthetic and qualitative view at fuzzy sets and their ensuing processing. Rajati and Mendel [40] proposed and demonstrated an effective methodology for implementing the generalized extension principle to solve Advanced Computing with Words problems using ordinary fuzzy sets.
4.2. Interval-valued fuzzy sets
An interval-valued fuzzy set (IVFS) is a special case of type 2 fuzzy set. An IVFS is defined by a mapping F from the universe U to the set of closed intervals in [0, 1]. Let F(u) = [F*(u), F*(u)]. The union, intersection and complementation of IVFSs are obtained by canonically extending fuzzy set-theoretic operations to intervals.
A brief history of interval-valued fuzzy sets (IVFSs) from its origin to our day can be given as follows. This review covers only the theoretical developments in the history of IVFSs chronically.
Interval-valued fuzzy sets were introduced independently by Zadeh [41], Grattan-Guiness [42], Jahn [43], and Sambuc [44]. Later Gorzałczany [45] introduced a method of approximate inference which operates on the extension of the concept of a fuzzy set by the concept of an interval-valued fuzzy set. Gorzałczany [46] presented a short analysis of formal properties of the interval-valued fuzzy inference methods. Turksen [47] proposed an interval-valued fuzzy set approach for approximate reasoning. Turksen and Zhong [48] proposed an Approximate Analogical Reasoning Schema, which exhibits the advantages of Fuzzy set theory and Analogical Reasoning in Expert Systems development. Turksen [49] showed that the ‘Compensatory And’, based on Zimmermann’s experimental results, is included within the boundaries of the ‘Interval-Valued Fuzzy Set And’ and the ‘Interval-Valued Fuzzy Set Or’ based on normal forms. Turksen and Tian [50] used interval-valued fuzzy sets to represent multiple antecedent S-implications based on normal forms where linguistic connectives, antecedents, and consequents are assumed to be fuzzy.
Turksen [51] proposed interval valued fuzzy set generated by fuzzy disjunctive and conjunctive normal forms to be a model of type II fuzzy sets to represent the second order semantic uncertainty realized by the combination of two or more fuzzy, vague, linguistic concepts by linguistic connectives. Gehrke et al. [52] presented a framework for fuzzy set theory in which fuzzy values are intervals. Turksen [53] examines non-specificity as a characteristic of interval-valued fuzzy sets. Chen et al. [54] proposed a bidirectional approximate reasoning method based on interval-valued fuzzy sets, where fuzzy production rules are used for knowledge representation, and the fuzzy terms are represented by interval-valued fuzzy sets.
Wang and Li [55] introduced the correlation coefficient of interval-valued fuzzy numbers, and studied some of their properties. Bustince [56] studied two methods for inference in approximate reasoning based on interval-valued fuzzy sets, the inclusion grade indicator and the similarity measure. Bustince and Burillo [56] introduced interval-valued fuzzy relations between sets X and Y as fuzzy subsets of the cartesian product X × Y, and they chose t-norms and t-conorms in such a way that as many properties of relations in 2-valued logic were preserved.
Grzegorzewski [57] suggested new methods for measuring distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets, based on the Hausdorff metric. Deschrijver and Kerre [58] introduced aggregation operators on the lattice L*, which is the underlying lattice of both interval-valued fuzzy sets and intuitionistic fuzzy sets in the sense of Atanassov. Dubois and Prade [59] focused on interpretations of interval-valued fuzzy set extensions.
Zeng and Li [60] introduced concepts of entropy of interval valued fuzzy set which is different from Bustince and Burillo [61] and similarity measure of interval valued fuzzy sets. Deschrijver [62] introduced the Archimedean property of t-norms on the lattice LI, where LI is the underlying lattice of interval-valued fuzzy set theory and intuitionistic fuzzy set theory. Deschrijver [63] introduced the addition, subtraction, multiplication and division on LI, where LI is the underlying lattice of both interval-valued fuzzy set theory and intuitionistic fuzzy set theory, and investigated some algebraic properties of these operators. Vlachos and Sergiadis [64] presented a unified formulation of subsethood, entropy, and cardinality for interval-valued fuzzy sets (IVFSs) and proposed an axiomatic skeleton for subsethood measures in the interval-valued fuzzy setting, in order for subsethood to reduce to an entropy measure. Deschrijver and Cornelis [65] compared different ways of representing operations on interval-valued fuzzy sets by corresponding operations on fuzzy sets and studied their intuitive semantics. Deschrijver and Král [66] presented a possible extension of the axiomatic theory of scalar cardinalities of fuzzy sets with finite support to interval-valued fuzzy set theory.
Yager [67] described the representation of a fuzzy subset in terms of its crisp level sets. Bustince et al. [68] presented the interval-valued fuzzy set theory, interval-valued information measures, and interval-valued fuzzy implication operators. Zeng and Guo [69] introduced an axiomatic definition of an interval-valued fuzzy sets’ inclusion measure and investigated the relationship among the normalized distance, the similarity measure, the inclusion measure, and the entropy of interval-valued fuzzy sets in detail. Yang et al.[70] introduced the concept of the interval-valued fuzzy soft set and defined the complement, “AND” and “OR” operations on the interval-valued fuzzy soft sets.
Bustince et al. [71] presented a method to construct interval-valued fuzzy sets from a matrix, in such a way that they obtained the length of the interval representing the membership of any element to the new set from the differences between the values assigned to that element and its neighbors in the starting matrix. Zhang et al.[72] proposed a new axiomatic definition of entropy of interval-valued fuzzy sets (IVFSs) and discussed its relation with similarity measure.
Hedayati [73] introduced the concept of quasi-coincidence of an interval-valued fuzzy set and the notion of interval-valued (α, β)-fuzzy k-ideals of semirings, which is a generalization of a fuzzy k-ideal. Van Gasse et al. [74] proved that the so-called pseudo prelinear triangle algebras are subdirect products of pseudo-linear triangle algebras. Deschrijver [75] gave the characterizations of the class of continuous t-norms on LI, where LI is the lattice of closed subintervals of the unit interval. Liu [76] discussed the approximate reasoning problems with interval-valued fuzzy environments based on the fully implicational idea and constructed a class of interval-valued fuzzy implications by means of a type of implications. Bustince [77] explained the reasons for which, for some specific problems, interval-valued fuzzy sets must be considered a basic component of Soft Computing. Deschrijver [78] studied t-norms on the lattice of closed subintervals of the unit interval and focused on t-norms which are meet-morphisms. Han and Chen [79] gave new roughness measure-rough entropy of the interval-valued fuzzy sets in an approximation space by using the information entropy theory. González-del-Campo et al.[80] proposed some axiomatic definitions about specificity for interval-valued fuzzy sets and showed some examples of measures of specificity for interval-valued fuzzy sets. Deschrijver [81] studied the uninorms which are neither conjunctive nor disjunctive in interval-valued fuzzy set theory.
Baczyński [82] discussed the distributive equation of implications I(x,T1(y,z))=T2(I(x,y),I(x,z)) over t-representable t-norms generated from nilpotent t-norms in interval-valued fuzzy set theory. Gorjanac Ranitović and Petojević [83] gave a solution of the problem of the interval-valued fuzzy sets synthesis and presented the necessary and sufficient conditions for a family of subsets to be a family of cut sets of an interval-valued fuzzy set.
Salazar and Soriano [84] showed a short characterization of embedded fuzzy sets of an interval-valued fuzzy set. They proved that any embedded fuzzy set can be always expressed as a convex combination of three fuzzy sets.
4.3. Type-n Fuzzy Sets
Zadeh [41] introduced type-2 fuzzy sets in 1978. A type-2 fuzzy set lets us incorporate uncertainty about the membership function into the fuzzy set theory. A type-2 fuzzy set
A brief history of type-n fuzzy sets from its origin to our day can be given as follows. This review covers only the theoretical developments in the history of type-2 fuzzy sets chronically.
Mizumoto and Zimmerman [85] and Mizumoto and Tanaka [86] developed the properties of type-2 fuzzy sets including algebraic product and sum. Karnik and Mendel [87] [88] defined type-reduction, the technique used as the first stage for defuzzifying type-2 fuzzy sets, by applying the extension principle to a variety of type-1 defuzzifiers. Fisher et al. [89] explored the fuzzy representation of higher order vagueness with respect to spatial phenomena. They initially related the arguments on philosophical vagueness to Type n Fuzzy sets. They showed that the Type 2 Fuzzy sets can be populated by using alternative parameterizations of a peak detection algorithm. Rickard et al. [90] extended Kosko’s definition of subsethood to Type-n fuzzy sets, for which subsethood is a Type-(n−1) fuzzy set on the unit interval. They showed how to compute subsethood for general Type-2 and interval Type-3 fuzzy sets. Aisbett [91] recursively extended the fundamental set theory operations of intersection and union to Type-3 and higher level fuzzy sets. They assumed a generalized form of convexity and normality. Turksen [92] described how one can generate Full Type 2 membership value distributions for a development of second order fuzzy system models with the proposed second order data analysis. He also suggested that a recursive restatement of FCM algorithm can allow the generation of Full Type 3 and Type n fuzzy system models if one were to investigate such system models in the future.
4.4. Intuitionistic Fuzzy Sets
Atanassov’s [93] intuitionistic fuzzy sets (IFSs) include the membership value as well as the non-membership value for describing any x in X such that the sum of membership and non-membership is at most equal to 1. Let X≠∅ be a given set. An intuitionistic fuzzy set in X is an object A given by
A brief history of intuitionistic fuzzy sets from its origin to our day can be given as follows. This review covers only the theoretical developments in the history of IFSs chronically.
Atanassov and Gargov [94] introduced a generalization of intuitionistic fuzzy set based on ordinary interval valued fuzzy sets and this generalization was defined as interval valued intuitionistic fuzzy set. Atanassov [95] introduced two new operators on intuitionistic fuzzy sets, namely modal operator-necessity and possibility; topological operator-interior and closure. Atanassov [96] defined new types of operations over the intuitionistic fuzzy sets. Atanassov [97] defined various operators for the interval valued intuitionistic fuzzy sets and their basic properties. Bustince and Burillo [98] recapitulated the definition given by Atanassov of intuitionistic fuzzy sets as well as the definition of vague sets given by Gau and Buehrer [99] and saw that both definitions coincide. Burillo and Bustince [98] defined the distance measure between intuitionistic fuzzy sets and gave an axiom definition of intuitionistic fuzzy entropy. Szmidt and Kacprzyk [100] proposed a geometrical representation for distances between intuitionistic fuzzy sets. Szmidt and Kacprzyk [101] proposed a non-probabilistic-type entropy measure for intuitionistic fuzzy sets, which is a result of a geometric interpretation of IFS. They introduced new definitions and compared with the approach used for ordinary fuzzy sets. Dengfeng and Chuntian [102] introduced the degree of similarity between intuitionistic fuzzy sets and proposed several new similarity measures between IFSs. These similarity measures of IFSs are applied to pattern recognitions. Liang and Shi [103] proposed several new similarity measures and proved the relationships between some similarity measures. Cornelis et al. [104] intended to fill an obvious gap by introducing a new definition of intuitionistic fuzzy rough sets, as the most natural generalization of Pawlak’s original concept of rough sets. Hung and Wang [105] presented a new method for similarity measures between intuitionistic fuzzy sets (IFSs) on the basis of the Hausdorff distance. Cornelis et al. [106] defined a clear and formal characterization of the mathematical models for the definition of implication within two settings: within intuitionistic fuzzy set theory and within interval-valued fuzzy set theory. Grzegorzewski [57] developed new methods for measuring distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets, based on the Hausdorff metric. Li [107] worked on intuitionistic fuzzy multiattribute decision making and constructed several linear programming models to generate optimal weights for attributes. Xu and Yager [108] developed some new geometric aggregation operators, such as the intuitionistic fuzzy weighted geometric (IFWG) operator, the intuitionistic fuzzy ordered weighted geometric (IFOWG) operator, and the intuitionistic fuzzy hybrid geometric (IFHG) operator, which extend the WG and OWG operators. Some numerical examples are given to illustrate the developed operators. Liu and Wang [109] developed new methods for solving intuitionistic fuzzy multi-criteria decision-making problems and introduced intuitionistic fuzzy point operators which reduce the degree of uncertainty of the elements.
Xu and Yager [110] defined the notions of intuitionistic fuzzy variable and uncertain intuitionistic fuzzy variable, and two new aggregation operators, dynamic intuitionistic fuzzy weighted averaging (DIFWA) operator and uncertain dynamic intuitionistic fuzzy weighted averaging (UDIFWA) operator. Zhou and Wu [111] proposed a general framework for the study of relation-based intuitionistic fuzzy rough approximation operators within which both constructive and axiomatic approaches are used. Zhou et al. [112] presented a general framework for the study of relation-based (I, T)-intuitionistic fuzzy rough sets by using constructive and axiomatic approaches. Mursaleen and Mohiuddine [113] studied the concept of statistically convergent and statistically Cauchy double sequences in intuitionistic fuzzy normed spaces.
Wei [114] developed some new group decision making analysis methods and proposed two new aggregation operators, induced intuitionistic fuzzy ordered weighted geometric (I-IFOWG) operator and induced interval-valued intuitionistic fuzzy ordered weighted geometric (I-IIFOWG) operator. Xu [115] used the Choquet integral to propose some intuitionistic fuzzy aggregation operators. The operators not only consider the importance of the elements or their ordered positions, but also can reflect the correlations among the elements or their ordered positions. Zhang et al. [116] proposed a new information entropy measure of interval-valued intuitionistic fuzzy set (IvIFS) which complies with the extended form of Deluca-Termini axioms for fuzzy entropy. They presented the cross-entropy of IvIFSs and discussed the relationship between the proposed entropy measures and the existing information measures of IvIFSs. Zhao et al. [117] developed some new generalized aggregation operators, such as generalized intuitionistic fuzzy weighted averaging operator, generalized intuitionistic fuzzy ordered weighted averaging operator, generalized intuitionistic fuzzy hybrid averaging operator, generalized interval-valued intuitionistic fuzzy weighted averaging operator, generalized interval-valued intuitionistic fuzzy ordered weighted averaging operator, and generalized interval-valued intuitionistic fuzzy hybrid average operator.
Ye [118] proposed a cosine similarity measure and a weighted cosine similarity measure between IFSs based on the concept of the cosine similarity measure for fuzzy sets. To demonstrate the efficiency of the proposed cosine similarity measures, the existing similarity measures between IFSs are compared with the cosine similarity measure between IFSs. Xu and Yager [119] investigated the Bonferroni mean (BM) under intuitionistic fuzzy environments. They developed an intuitionistic fuzzy BM (IFBM) and discussed its variety of special cases. Zeng and Su [120] considered the situation with intuitionistic fuzzy information and developed an intuitionistic fuzzy ordered weighted distance (IFOWD) operator. Li [121] developed a closeness coefficient based nonlinear programming method for solving multiattribute decision making problems in which ratings of alternatives on attributes are expressed using interval-valued intuitionistic fuzzy (IVIF) sets and preference information on attributes is incomplete. Nonlinear programming models are constructed on the concept of the closeness coefficient, which is defined as a ratio of the square of the weighted Euclidean distance between an alternative and the IVIF negative ideal solution (IVIFNIS) to the sum of the squares of the weighted Euclidean distances between the alternative and the IVIF positive ideal solution (IVIFPIS) as well as the IVIFNIS.
Wei and Zhao [122] investigated some multiple attribute group decision making problems in which both the attribute weights and the expert weights are usually correlative, attribute values take the form of intuitionistic fuzzy values or interval-valued intuitionistic fuzzy values. They developed two new aggregation operators, induced intuitionistic fuzzy correlated averaging (I-IFCA) operator and induced intuitionistic fuzzy correlated geometric (I-IFCG) operator. Wang and Liu [123] treated the intuitionistic fuzzy aggregation operators with the help of Einstein operations. They first introduced some new operations of Atanassov’s intuitionistic fuzzy set, such as Einstein sum, Einstein product, and Einstein scalar multiplication. Then, they developed some intuitionistic fuzzy aggregation operators, such as the intuitionistic fuzzy Einstein weighted averaging operator and the intuitionistic fuzzy Einstein ordered weighted averaging operator, which extend the weighted averaging operator and the ordered weighted averaging operator to aggregate Atanassovs intuitionistic fuzzy values, respectively. Yang and Chen [124] introduced three kinds of new operators: the quasi-intuitionistic fuzzy ordered weighted averaging operator, the quasiintuitionistic fuzzy Choquet ordered averaging operator and the quasi-intuitionistic fuzzy ordered weighted averaging operator based on the Dempster-Shafer belief structure.
Parvathi et al. [125] introduced linear regression analysis in an intuitionistic fuzzy environment using intuitionistic fuzzy linear models with symmetric triangular intuitionistic fuzzy number (STriIFN) coefficients. The goal of this regression is to find the coefficients of a proposed model for all given input-output data sets. The coefficients of an intuitionistic fuzzy regression (IFR) model are found by solving a linear programming problem (LPP). Yu and Xu [126] investigated the prioritization relationship of attributes in multi-attribute decision making with intuitionistic fuzzy information and developed a new method for comparing two IFVs, based on which the basic intuitionistic fuzzy operations satisfy monotonicities. Yu [126] studied the multi-criteria decision making problem with the assumption that the criteria are correlative under intuitionistic fuzzy environment. Some new aggregation operators for intuitionistic fuzzy information are proposed, including the intuitionistic fuzzy geometric Heronian mean (IFGHM) operator and the intuitionistic fuzzy geometric weighed Heronian mean (IFGWHM) operator. Zhao and Wei [127] developed some new Einstein hybrid aggregation operators, such as the intuitionistic fuzzy Einstein hybrid averaging (IFEHA) operator and intuitionistic fuzzy Einstein hybrid geometric (IFEHG) operator, which extend the hybrid averaging (HA) operator and the hybrid geometric (HG) operator to accommodate the environment in which the given arguments are intuitionistic fuzzy values. Farhadinia and Ban [128] gave a novel method to extend a similarity measure of generalized trapezoidal fuzzy numbers (GTFNs) to similarity measures of generalized trapezoidal intuitionistic fuzzy numbers (GTIFNs) and generalized interval-valued trapezoidal fuzzy numbers (GIVTFNs) such that the initial properties to be preserved.
Liu [129] developed group decision-making methods based on some Hamacher aggregation operators, which extended the algebraic aggregation operators and Einstein aggregation operators. He proposed an interval-valued intuitionistic fuzzy Hamacher weighted averaging operator, interval-valued intuitionistic fuzzy Hamacher-ordered weighted averaging operator, interval-valued intuitionistic fuzzy Hamacher hybrid weighted averaging operator, interval-valued intuitionistic fuzzy Hamacher geometric weighted averaging operator, interval-valued intuitionistic fuzzy Hamacher geometric-ordered weighted averaging operator, and interval-valued intuitionistic fuzzy Hamacher geometric hybrid weighted averaging operator. Szmidt et al.[130] addressed the problem of how to measure the amount of knowledge conveyed by the Atanassov’s intuitionistic fuzzy set. Liao and Xu [131] investigated a new approach to derive the priority weights from an intuitionistic fuzzy preference relation (IFPR). They gave a new definition of multiplicative consistent IFPR and proposed a formula, which involves the underlying intuitionistic fuzzy weights of the IFPR. Iancu [132] proposed different types of similarity measures for intuitionistic fuzzy sets and extended some crisp cardinality measures to measures for intuitionistic fuzzy sets; the main role in this process is played by the Frank t-norm family.
Lei and Xu [133] described the change values of IFNs when considering them as variables and classified these change values based on the basic operations for IFNs. They depicted the convergences of sequences of IFNs by the subtraction and division operations. Montes et al. [134] dealt with the problem of comparison of intuitionistic fuzzy sets and presented an axiomatic definition of divergence measures for IFSs. Lei et al. [135] defined two subtraction and division operations of IFNs, and developed a sequence of general integrals dealing with continuous intuitionistic fuzzy data based on Archimedean t-conorm and t-norm.
4.5. Fuzzy Multisets
Let X be a nonempty set. A fuzzy multiset à drawn from X is characterized by a function, “count membership” of à denoted CMA by such that CMA : X → Q where Q is the set of all crisp multisets drawn from the unit interval [0, 1]. Then for any x ∈ X, the value CMA(x) is a crisp multiset drawn from [0, 1]. For each x ∈ X, the membership sequence is defined as the decreasingly ordered sequence of elements in CMA(x). It is denoted by
A brief history of fuzzy multisets which are also called fuzzy bags from its origin to our day is given as follows. This review covers only the theoretical developments in the history of fuzzy multisets chronically.
Yager [136] introduced the bag structure as a set-like object in which repeated elements were significant. He discussed operations on bags such as intersection, union and addition and introduced the operation of selecting elements from a bag based upon their membership in a set and showed the usefulness of the bag structure in relational data bases. Ramer and Wang [137] proposed a design based on extending the notion of a fuzzy set to a fuzzy multiset. They showed that the set of the discrete, n-element fuzzy numbers becomes a topological space in this fashion. Kim and Miyamoto [138] introduced basic relations and operations of fuzzy multisets and their theoretical properties using a grade sequence.
Syropoulos [139] summarized the basic elements of the multiset theory and described multisets and the operations between them and presented hybrid sets and their operations. Miyamoto [140] considered fuzzy multisets with infinite membership sequences and their generalization using set-valued memberships and defined two metric spaces of the infinite fuzzy multisets in terms of cardinality. Miyamoto [141] developed a method of fuzzy clustering based on fuzzy multisets and discussed data clustering in relation to information retrieval models. He proposed two dissimilarity measures on fuzzy multisets. Miyamoto [142] proposed a class of generalized multisets that includes real-valued multisets, fuzzy number-valued multisets, and fuzzy multisets and defined upper and lower approximations of the generalized multisets.
Miyamoto [143] proposed a fuzzy multiset model for information clustering with application to information retrieval on the WWW. Miyamoto and Mizutani [144] considered a space of fuzzy multisets and applied to clustering of documents/terms for information retrieval and studied fuzzy c-means clustering algorithms with kernel functions in support vector machines. Mizutani and Miyamoto [145] proposed a method of fuzzy clustering based on a fuzzy multiset model and proposed a dissimilarity measure on fuzzy multisets and a method of fuzzy c-means using this measure.
Miyamoto and Mizutani [146] overviewed a fuzzy multiset model as a model of information retrieval on the WWW and developed a family of fuzzy document clustering algorithms. Miyamoto [147] reviewed the basics of multisets and fuzzy multisets and proved the fundamental properties of fuzzy multisets, and defined advanced operations. Miyamoto [148] reviewed three classes of generalizations of multisets, which are real-valued multisets, fuzzy number-valued multisets, and fuzzy multisets. Miyamoto [149] gave an overview of data structures and operations for fuzzy multisets. A simple linear list identified with an infinite dimensional vector was taken as an elementary data structure for fuzzy multisets.
Torra and Miyamoto [150] studied fuzzy c-means and compared their application to fuzzy sets and fuzzy multisets. Miyamoto [151] gave two remarks on basic aspects of fuzzy sets. They are the notation for the α-cuts and a commutative property in the extension principle.
Matthe et al. [152] presented the theoretical aspects of calculating the similarity between sets, and its generalizations multisets, fuzzy sets and fuzzy multisets. Mizutani et al. [153] developed clustering algorithms based on a fuzzy multiset model for document clustering in which the standard proximity measure of the cosine correlation is generalized.
Casasnovas and Rossello [154] defined in an axiomatic way scalar and fuzzy cardinalities of finite multisets over ]0, 1], and obtained explicit descriptions for them. Meyer and Hornik [155] presented data structures and algorithms for sets and some generalizations available for R through the sets package. Wang et al. [156] proposed a novel clustering method based on fuzzy multisets, in which the fuzzy multiset is adopted to characterize user’s navigation behavior and to construct a multi fuzzy similar matrix to represent similarity between different users’ browsing behavior. Murai et al. [157] made some basic consideration for reformulating roles of sequences in uncertain information processing and reformulated näive subsets and multisets as some quotient sets induced from free monoids as the set of finite sequences.
Bedregal et al. [158] presented a generalization of Atanassov’s operators to higher dimensions and used the concept of fuzzy set, which can be seen as a special kind of fuzzy multiset, to define a generalization of Atanassov’s operators for n-dimensional fuzzy values. Zhu et al. [159] proposed dual hesitant fuzzy sets (DHFSs), which encompass fuzzy sets, intuitionistic fuzzy sets, hesitant fuzzy sets, and fuzzy multisets as special cases. Syropoulos [160] presented an orthogonal approach to the fuzzification of both multisets and hybrid sets and introduced L-multi-fuzzy and L-fuzzy hybrid sets, which are general enough and in spirit with the basic concepts of fuzzy set theory.
Murai et al. [161] focused on the two definitions of fuzzy multisets by Yager and Minamoto, respectively, and examined their difference in the framework of granular hierarchical structures generated from free monoids. Wang et al. [162] defined the correlation measures for dual hesitant fuzzy information and then discussed their properties in detail.
Singh [163] proposed the axiom definition of a similarity measure between dual hesitant fuzzy sets and presented a new similarity measure considering membership and nonmembership degrees of dual hesitant fuzzy sets. Singh [164] introduced the axiom definition of a similarity measure between dual hesitant fuzzy sets and presented a new similarity measure considering membership and nonmembership degrees of dual hesitant fuzzy sets. Tanaka et al.[165] proposed granular hierarchical structures generated from free monoids in order to provide a unified basis for various extended concepts of sets like multisets, fuzzy sets and others. Murai et al. [166] introduced crisp and fuzzy granular hierarchical structures and found that there are two kinds of different preextensions between Yager’s fuzzy multisets and Zadeh’s fuzzy sets. Yue et al. [167] developed an effective framework to solve object merging problem based on fuzzy multisets and defined quality measures of purity and entropy to quantify the quality of the solutions. Lizasoain and Ochoa [168] extended the concept of an ordered weighted quasi-average operator and an n-dimensional Atanassov’s operator from fuzzy multisets on [0,1] to fuzzy multisets on any complete lattice endowed with a tnorm and a t-conorm.
Murai et al. [169] focused on the two definitions of fuzzy multiset operations, one by Yager and the other by Miyamoto and examined their differences in the framework of granular hierarchical structures generated from the free monoids. Corsini [170] studied connections between fuzzy multisets and hyper structures and determined conditions such that the hyper structure associated with a fuzzy multiset may be a quasi-join space.
4.6. Nonstationary fuzzy sets
Let à denote a fuzzy set of a universe of discourse X characterized by a membership function μÃ. Let T be a set of time points ti (possibly infinite) and f : T → ℜ denote a perturbation function. A non-stationary fuzzy set à of the universe of discourse X is characterized by a non-stationary membership function μà : T × X → [0, 1] which associates each element (t, x) of T × X with a time-specific variation of μÃ(x). The non-stationary fuzzy set à is denoted by:
A brief history of nonstationary fuzzy sets from its origin to our day is given as follows. This review covers only the theoretical developments in the history of nonstationary fuzzy sets chronically.
Garibaldi and Ozen [171] presented a case study in which the introduction of vagueness or uncertainty into the membership functions of a fuzzy system was investigated in order to model the variation exhibited by experts in a medical decision-making context through nonstationary fuzzy reasoning. Asadov and Nabiev [172] formulated two problems and resolved in optimizing nonstationary fuzzy and deterministic systems. Garibaldi et al. [173] introduced the notion termed a “nonstationary fuzzy set” and presented the concept of a perturbation function that is used for generating nonstationary fuzzy sets and gave the definitions of the basic set operators for nonstationary fuzzy sets together with proofs of selected properties of these operators. Leite et al. [174] introduced an evolving fuzzy granular framework to learn from and model time-varying fuzzy input-output data streams. The framework is particularly suitable to handle potentially unbounded fuzzy data streams and render singular and granular approximations of nonstationary functions.
4.7. Hesitant Fuzzy Sets
Hesitant fuzzy sets (HFSs), initially developed by Torra [175], are the extensions of regular fuzzy sets which handle the situations where a set of values are possible for the membership of a single element.
Torra [175] defines hesitant fuzzy sets (HFSs) as follow: Let X be a fixed set, a HFS on X is in terms of a function that when applied to X returns a subset of [0, 1]. Mathematical expression for HFS is as follows:
A brief history of hesitant fuzzy sets from its origin to our day can be given as follows. This review covers only the theoretical developments in the history of HFSs chronically.
Torra and Narukawa [176] defined hesitant fuzzy sets and presented an extension principle, which permits to generalize existing operations on fuzzy sets to this new type of fuzzy sets. Torra [175] proposed hesitant fuzzy sets (HFS) and introduced some basic operations for HFS. He proved that the envelope of the hesitant fuzzy sets was an intuitionistic fuzzy set. Xu and Xia [177] proposed a variety of distance measures for hesitant fuzzy sets, based on which the corresponding similarity measures could be obtained and investigated the connections of the aforementioned distance measures. Rodriguez et al. [178] introduced the concept of a hesitant fuzzy linguistic term set to provide a linguistic and computational basis to increase the richness of linguistic elicitation based on the fuzzy linguistic approach and the use of context-free grammars by using comparative terms. Zhu et al. [159] proposed dual hesitant fuzzy sets (DHFSs), which encompass fuzzy sets, intuitionistic fuzzy sets, hesitant fuzzy sets, and fuzzy multisets as special cases and investigated the basic operations and properties of DHFSs. Chen et al. [179] derived some correlation coefficient formulas for HFSs and applied them to clustering analysis under hesitant fuzzy environments. Farhadinia [128] investigated the relationship between the entropy, the similarity measure and the distance measure for hesitant fuzzy sets (HFSs) and interval-valued hesitant fuzzy sets (IVHFSs). Yu [180] extended traditional hesitant fuzzy sets to Triangular Fuzzy Hesitant Fuzzy Sets (TFHFS), in which the membership degree of an element to a given set is expressed by several possible triangular fuzzy numbers and proposed a series of aggregation operators for TFHFEs. Sun and Liu [181] proposed two normalized weighted geometric Bonferroni Means (BM), and studied some properties of the proposed operators.
Wang et al. [162] defined the correlation measures for dual hesitant fuzzy information and discussed their properties in detail. Qian et al. [182] extended hesitant fuzzy sets by intuitionistic fuzzy sets and referred to them as generalized hesitant fuzzy sets and redefined their basic operations. Liao et al.[183] developed different types of distance and similarity measures for HFLTSs to enhance and extend the applicability of HFLTSs. Ye [184] proposed a correlation coefficient between DHFSs as a new extension of existing correlation coefficients for hesitant fuzzy sets and applied it to multiple attribute decision making under dual hesitant fuzzy environments. Wei et al.[185] defined operations on HFLTSs and gave possibility degree formulas for comparing HFLTSs. They also defined two aggregation operators for HFLTSs. Wang et al. [186] focused on multi-criteria decision-making problems in which the criteria were in different priority levels and the criteria values took the form of interval-valued hesitant fuzzy linguistic numbers (IVHFLNs). The new approach was based on the prioritized aggregation operators of IVHFLNs. Liao and Xu [187] proposed two new basic operations over HFSs, which are the subtraction operation and the division operation. The relationship between intuitionistic fuzzy sets (IFS) and HFS was verified in terms of these two operations.
Farhadinia [188] extended the hesitant fuzzy set to its higher order type and referred to it as the higher order hesitant fuzzy set. Farhadinia [189] presented a series of score functions for hesitant fuzzy sets providing a variety of new methods for ranking HFSs. Farhadinia [190] proposed dual interval-valued hesitant fuzzy sets, which encompass fuzzy sets and its aforementioned extensions as special cases and put forward some formulas to create new correlation coefficients for fuzzy sets and its extensions in a general way. Zhu and Xu [191] developed typical DHFSs (T-DHFSs) and presented their operations and properties.
Yang et al. [192] developed both constructive and axiomatic approaches. They presented a model of hesitant fuzzy rough sets in constructive approach to approximate a hesitant fuzzy target through a hesitant fuzzy relation whereas they presented an operators-oriented characterization of the hesitant fuzzy rough set in axiomatic approach. Peng et al. [193] developed the definition of hesitant interval-valued intuitionistic fuzzy sets (HIVIFSs) based on interval-valued intuitionistic fuzzy sets (IVIFSs) and hesitant fuzzy sets (HFSs). In addition, they proposed some hesitant interval-valued intuitionistic fuzzy number aggregation operators based on t-conorms and t-norms. Chen and Xu [194] derived the properties and relationships of fundamental operations on IVHFSs for Algebraic t-norm and tconorm. Rodriguez et al.[195] presented an overview on hesitant fuzzy sets with the aim of providing a clear perspective on the different concepts, tools and trends related to this extension of fuzzy sets.
Wei et al. [196] proposed a variety of distance measures for hesitant interval-valued fuzzy sets, based on which the corresponding similarity measures can be obtained. They investigated the connections of the aforementioned distance measures and further developed a number of hesitant interval-valued ordered weighted distance measures and hesitant interval-valued ordered weighted similarity measures. Wang et al.[197] defined hesitant fuzzy soft sets by combining fuzzy soft sets with hesitant fuzzy sets and also defined some operations on hesitant fuzzy soft sets based on Archimedean t-norm and Archimedean t-conorm. Hu et al. [198] proposed the concept of interval type-2 hesitant fuzzy set (IT2HFS), which is a generalization of interval type-2 fuzzy set and hesitant fuzzy set. Pérez-Fernández [199] developed the orders between finite interval-valued hesitant fuzzy sets and introduced finite interval-valued hesitant fuzzy preference relations. Zhang and Yang [200] defined a new partial order for typical hesitant fuzzy elements (THFEs) via the disjunctive semantic meaning of a set, based on which fuzzy inclusion relationship was defined for THFSs. Farhadinia [201] presented a novel HFS ranking technique based on the idea of lexicographical ordering. Rodriguez et al. [202] studied the necessity of HFSs and provided a discussion about current proposals including a guideline that the proposals should follow and some challenges of HFSs.
5. Future of Fuzzy Sets
The literature review above proves that an extraordinary interest to the fuzzy set theory exists among researchers all over the world. However, there is still a resistance not to accept the fuzzy set theory as a formal science by some scientists [3]: Some harsh comments from those scientists are as follows: “Fuzzification is a kind of scientific permissiveness; it tends to result in socially appealing slogans unaccompanied by the discipline of hard scientific work and patient observation.”, “The danger of fuzzy theory is that it will encourage the sort of imprecise thinking that has brought us so much trouble.”, “Anything that can be done with fuzzy logic, belief functions, upper and lower probabilities, or any other alternative to probability can better be done with probability.”, and “Since neither of the main arguments that are offered in its favor is acceptable, I conclude that we do not need fuzzy logic.” Although these negative comments about the fuzzy set theory still exist, the theory has expanded with an enormous acceleration.
Especially, the technologies using fuzzy control have emerged in the market such as washing machines, video cameras, cranes, subway trains, etc. The views completely against the theory are losing their meanings as its real world applications appear in the market.
One of the present problems related to the future of the fuzzy set theory is the need for a common notation since we frequently encounter different notations for the same concepts of the theory in the publications. A common notation will improve the value of the theory and will be a significant step to provide the condition that has already been implemented in the classical logic. Another problem that will probably be solved by itself in the future is the segregation between the classical logic publications and the fuzzy logic publications. Presently, the undergraduate level books do not include subsections handling the problems with imprecise data. In the future, we expect the contents of an undergraduate level book to be composed of the topics with both imprecise data and precise data without indicating it on the cover page. For instance, the classical books of operations research, engineering economics, multicriteria decision-making, statistics, etc. will possibly include fuzzy analyses even it is not indicated on the cover page. On the contrary, it is expected that the journals or books whose titles include “fuzzy sets” or “ fuzzy systems” such as Fuzzy Sets and Systems, International Journal of Fuzzy Systems, etc. will continue to appear among the others in the future since significant contributions to the fuzzy set theory seem to continue along many years.
Too many different fuzzy models and approaches for the solution of a certain problem without sufficient discussions about their correctness or deficiencies may create a doubtful point of view to the theory. The publishers, editors-in-chiefs, editors, and area editors must establish necessary and sufficient conditions for the perfect review processes of these models and approaches. Unfortunately, it is seen that type-2 error often occurs at the final decision stage for many papers.
New extensions of fuzzy sets generally focus on the detailed and better definition of discrete or continuous membership functions for the elements belonging to a set. All these efforts try to yield a better definition of uncertainty, imprecision, and vagueness, thus a better control of uncertainty to create a similar system having human thinking style. It is clear that all these extensions will be utilized to improve the quality of the outputs of the fuzzy technologies in the future. The intelligent human robots of the future will possibly decide and behave based on the latest fuzzy control principles.
6. Conclusion
Even the fuzzy set theory is a young theory, whose age is only 50; it has covered a lot of ground by today. Even there are still some researchers against it; numerous invaluable researchers delivered its present status to the world. Almost every branch of science, from engineering to social sciences, from decision sciences to computer sciences, and from physical sciences to life sciences, utilized the theory with a great success [203].
Extensions of fuzzy sets are the focal point of the present studies. Intuitionistic fuzzy sets take the first rank that researchers prefer utilizing them in their studies. Hesitant fuzzy sets take the second rank in this manner. Type-2 fuzzy sets take the third rank even they are older than the first two extensions. It is possible that more extensions of fuzzy sets will appear in the future, each trying to define membership functions with a different point of view.
The place where the fuzzy set theory has reached in its 50th year is quite far from its origin but the theory needs much time to arrive at the point it deserves. A search in Google for possibility theory gives only 93,000 pages in the Internet while that number is 2,660,000 for probability theory. A similar search for fuzzy set theory gives 451,000 pages.
We suggest a deeper analysis within subject areas for further research. For instance, in the subject area engineering, both theoretical works and practical works on the fuzzy set theory can be comprehensively analyzed. This will provide a better understanding of the value created by the fuzzy set theory.
References
Cite this article
TY - JOUR AU - Cengiz Kahraman AU - Başar Öztayşi AU - Sezi Çevik Onar PY - 2016 DA - 2016/04/01 TI - A Comprehensive Literature Review of 50 Years of Fuzzy Set Theory JO - International Journal of Computational Intelligence Systems SP - 3 EP - 24 VL - 9 IS - Supplement 1 SN - 1875-6883 UR - https://doi.org/10.1080/18756891.2016.1180817 DO - 10.1080/18756891.2016.1180817 ID - Kahraman2016 ER -
