1. INTRODUCTION

On February 11, 2020, WHO announced in Geneva, Switzerland, that the novel coronavirus pneumonia was named corona virus disease (COVID-19), referring to the pneumonia caused by the coronavirus 2019 infection. According to the existing statistical data, a small number of patients are accompanied by upper respiratory and digestive tract symptoms, e.g., nasal congestion, runny nose, and diarrhea [1]. To June 30, 2020, COVID-19 has affected more than 188 countries and regions around the world, with a total of 10,302,867 confirmed cases and 505,518 deaths.

The chest CT of COVID-19 patients shows patchy, flocculent, nodular, and exudative shadows in the subpleural area, which are usually dominated by double lower lungs according to the available chest CT data of COVID-19 patients. Ground glass opacity (GGO) was the main manifestation of the lesions. In critical patients, large fusion and mesh-like changes of GGO are observed [2]. Therefore, chest imaging is one of the common clues for the detection and diagnosis of COVID-19, and it is also an important focus for clinicians. For example, Pan et al. [3] found that the cause of the disease on lung computed tomography (CT) was positively correlated with the number of lesions, among which the median time point about 10 days after the onset was the most serious by CT score. Wang et al. [4] found from 93 cases of COVID-19 CT that 97.8% of patients’ lesions located in the pleura below. Ground glass shadows appeared in 74.2% of patients, and ground glass shadow detection in normal patients (79.5%) was higher than that in critically ill patients (55%). Consolidation shadows were present in 60.2% of patients, consolidation shadows detection in critically ill patients (90%) was higher than normal patients (52.1%). Bernheim et al. [1] concluded from the CT manifestations of 121 cases of COVID-19 that 17% of the patients had accumulated unilateral lung, the most common manifestation being ground glass shadow (which could be the only manifestation or coexisting with time-variant shadow), and only 2% of the patients had consolidation shadow on CT. In the 0–2 days after the onset, unilateral lung involvement was the most common. 56% of the patients presented normal CT appearance, 44% presented ground glass shadow, and 17% presented consolidation shadow. Both sides of the lungs were affected by 76% and 88% of patients 3–5 days after onset and 6–12 days after onset, respectively. Ground glass shadows were observed in 88% of the two groups, and consolidation shadows were observed in more than half of the patients [1]. Guan et al. [2] reported 840 cases of hospitalized patients with CT examinations, only 76.4% of the patients present with pneumonia, 50.0% and 46.0% of patients presented ground glass shadow and patchy shadow, respectively. Besides, local plaques were found in 37.2% of patients. In the case with a good treatment effect, the pulmonary CT performance gradually improved. In contrast, the pulmonary CT performance gradually worsened.

Recently, many researchers use computer vision and artificial intelligence to detect COVID-19, such as radial basis function neural network (RBFNN) [5], kernel-based extreme learning machine (KELM) [6], extreme learning machine with bat algorithm (ELMBA) [7]. Great progress has been achieved. However, in the course of performing the training algorithm of the classifier, they all face the situation of either falling into the local optimal [8,9] or failing to reach the global optimal.

To solve above issues, this study proposes a smart system to diagnose COVID-19 by using wavelet Renyi entropy (WRE) and 3SBBO. It will help clinicians make more accurate judgments on patients’ conditions and even provide automatic diagnosis.

There are scholars using deep learning techniques in detecting COVID-19, Rosebrock [10] presented a guide for using deep learning (Keras and TensorFlow) to detect COVID-19. This guide can help readers learn sample diseased and healthy X-ray images, train CNNs to detect COVID-19 automatically, and evaluate their results. Maghdid et al. [11] shared a low-cost technique of using smartphone-embedded sensors to diagnose COVID-19. This is particularly helpful since many people are currently holding smartphones every day. Wang and Wong [12] published a DL framework (COVID-Net), which was adapted for detecting COVID-19 patients based on chest radiography scans. The authors also used an explainable method to acquire more meaningful understandings into vital elements linked with COVID cases.

In this study, as the dataset is relatively small, we used WRE as feature descriptors and feedforward neural network (FNN) [13,14] as the classifier instead of the deep learning, which is widely used in biomedical image analysis. We believe that the order of WRE is of great significance for image feature detection. However, existing optimization algorithms can only optimize weights and biases of FNN, such as genetic algorithm (GA)[15] and biogeography-based optimization (BBO) [16]. Therefore, we proposed a novel three-segment biogeography-based optimization (3SBBO) that can not only optimize the order of Renyi entropy (RE), but also optimizes the weights and biases of FNN. In all, our contributions are composed of those points: (1) Introduce WRE extraction method and prove it is suitable for chest CT images. (2) Propose a 3SBBO algorithm to optimize RE order, weights and biases simultaneously. (3) Present a more effective automatic detection method for COVID-19 based on chest CT.

The rest of the paper is organized as follows: Section 2 describes the method of dataset selection. Section 3 explains wavelet decomposition and WRE, describes the construction of the classifier, the proposed optimization method: 3SBBO, and also gives the corresponding evaluation method. The experiment design is given in Sections 4 and 5 gives the experimental results and the discussion of the results. Section 6 concludes the work. Table 5 provides variable definition and Table 6 shows all the abbreviations used in this paper.

2. DATASET

Our experimental dataset consists of 296 images from chest CT, including 148 images were taken from COVID-19 patients (41 males and 25 females). The remaining 148 images were taken from healthy subjects (31 males and 35 females).

The 66 COVID-19 patients and 66 healthy subjects were examined using Philips Ingenuity 64 row spiral CT machine, KV: 120, MAS: 240. Healthy subjects were randomly selected from healthy people (tested negative). All subjects are in a supine position, with both upper limbs lifted up, and exposed with breath-holding after deep inhalation. The scanning range is from the thoracic inlet to the costal diaphragm angle. Using tube voltage 110–130 kV and automatic tube current technology, scanning layer thick layer spacing is 3 mm. Resolution of images are 1024×1024.

All the sampled images are transmitted to medical image PACS for observation, and the most representative image is selected by two doctors who are experienced in COVID-19 diagnosis based on the characteristics of the CT. The screen method is as follows: for COVID-19 patients, the layer with the largest lesion features is selected. For healthy subjects, the image level could be selected at will. When two doctors disagree about the diagnosis of an image, a senior doctor should be consulted to reach an agreement. In the preparation of the experiment, a summary of the dataset is shown in Table 1. We do not collect age information, since our focus is to identify COVID-19 from chest CT images.

3. Methodology

Table 5 shows all variables used in this study, in order to ease the understanding of this paper. Table 6 gives the abbreviation and their full names.

3.2. Two-Dimensional Wavelet Decomposition

Assuming a given image can be symbolized by lm,n, two-dimensional DWT is performed on it. After each decomposition, four subbands (A₁, E₁, G₁, I₁) are generated, as shown in Figure 1, where subband A is the horizontal quadrant, subband E is the vertical quadrant, subband G is the diagonal quadrant, and subband I denotes the approximate component quadrant of l(m,n). The subscript “1” means 1-level decomposition subbands.

Figure 1

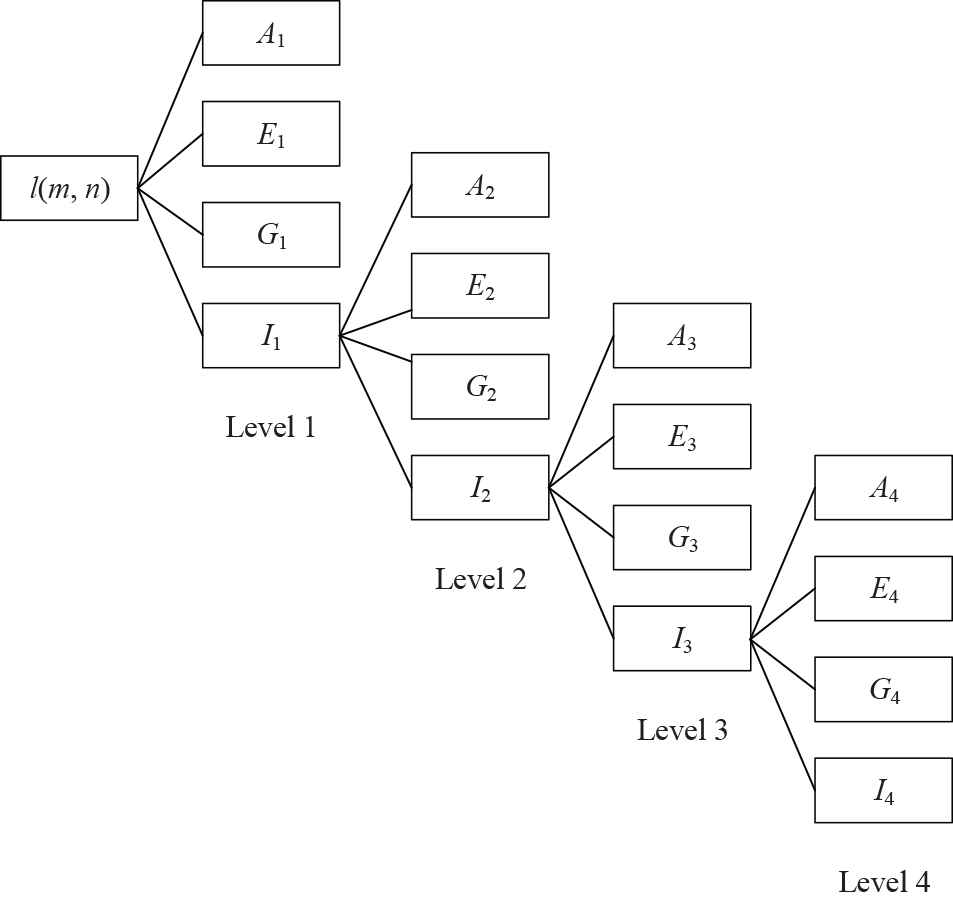
A toy example of a 4-level two-dimensional discrete wavelet transform (2D-DWT).

Subband I₁ can be decomposed into four other subbands at the second level. Figure 1 presents a toy example of 4-level decomposition. This study chose to use 3-level decomposition. The reason why we use 3-level decomposition is by trial-and-error method.

Mathematically, assume D represents a 2D-DWT operation, then we have

A1,E1,G1,I1=Dlm,n(7)

And subsequent decomposition as

A2,E2,G2,I2=DI1(8.a)

A3,E3,G3,I3=DI2(8.b)

A4,E4,G4,I4=DI3(8.c)

3.3. Basics of RE

Each element of the wavelet decomposition subband can be regarded as a discrete random variable Q, which takes on potential numerical values determined by random phenomenon as

Q~q1,q2,q3,⋅⋅⋅,qH(9)

Suppose the corresponding probability mass function (PMF) is

vh=PrQ=qh(10.a)

h=1,2,…,H(10.b)

The r-order RE [17] could be defined as

LrQ=11−rlog∑h=1Hvhr(11)

Here, r is a desirable real number of any value. The RE is Schur-concave and a nonincreasing function of r. Due to different values of r, RE can be converted into other types of information entropy [18]. For example,

LrQ=L1QShannon EntropyL0QHartley EntropyL∞QMin Entropy(12)

when r=1, L1Q is Shannon entropy; when r=0, L0Q is Hartley entropy; when r=∞, L∞Q is min-entropy.

Figure 2 shows the RE of different r values for a binary random variable (BRV) with its PMF as

Q′~q′1,q′2(13.a)

v′1=PrQ′=q′1(13.b)

v′2=PrQ′=q′2(13.b)

Figure 2

The Renyi entropy (RE) of various r values of a binary random variable (BRV) Q′.

It can be clearly seen that the concaveness and nonincreasing of r. Since v'1 being zero values does not alter the computation of RE, so it is included in Figure 2. In this figure, Matlab command “log2” is used.

3.4. Feedforward Neural Network

To train the classifier, we propose an algorithm that combines the FNN with 3SBBO. The FNN consists of three layers: an input layer, hidden neuron layers, and an output neuron layer. The connection mode between the neurons of each layer is full connection. Figure 3 is the structural diagram of FNN.

Figure 3

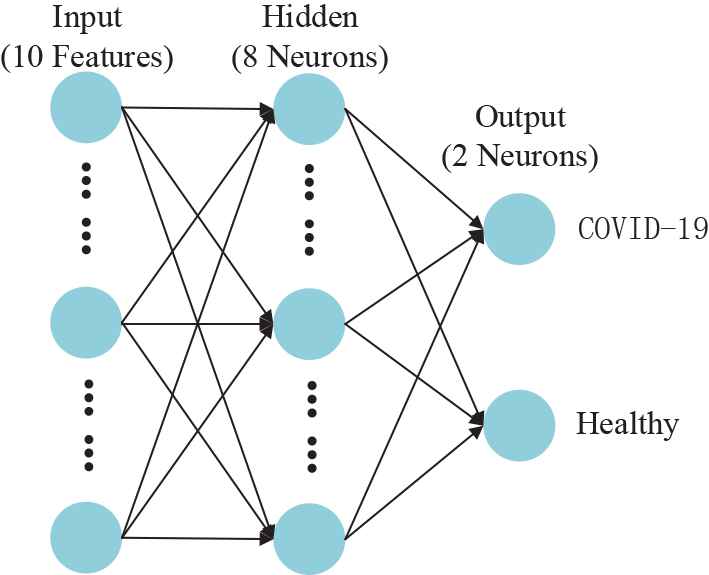
Structure diagram of feedforward neural network (FNN). (The structure if fixed by trial-and-error method)

In the experiment of this paper, we set the number of neurons in the hidden layer to 8 by manual trial-and-error. According to the general approximation theorem, FNN has powerful approximation ability, and it can approximate the corresponding expected output arbitrarily [19]. Although many classifiers such as support vector machine, decision tree, and naive Bayes are often used by some scholars in medical image analysis, the simple and practical FNN can better complete the difficult nonlinear mapping on the premise of less cost. Therefore, FNN is one of the network models of great significance and wide application in the field of medical image analysis.

Remember we use 3-level decomposition, so we will have 3×3+1=10 input features. Thus, the input to FNN is defined as

X=x1,x2,x3,…,x10T (14)

The size of hidden neuron is determined as 8, so the hidden layer output is defined as

Y=y1,y2,y3,…,y8T (15)

The output of FNN can be expressed as

O=o1,o2T (16)

Since we have to handle a binary classification in this study. Using simple math, we can update above two equations in matrix form as

Y=gW1X+b1 (17)

O=gW2Y+b2 (18)

where g represents the activation function. W1 and W2 represent the hidden layer weights and output weights, respectively. b1 and b2 represent the hidden layer bias and output layer bias, respectively.

For any given function τ (the ideal output, i.e., the target) and an arbitrarily small number θ>0, we know that O (the realistic output) can be used as an approximation realization of function τ, which satisfies the following representation.

|O−τ|<θ(19)

3.5. Standard BBO

BBO is an optimization algorithm with both good local and global solutions, which can show good convergence in image classification. There are many other excellent algorithms [20–27], which we will use into our task in the future.

3.5.1. Concepts of BBO

Figure 4 shows the corresponding relationship between BBO, GA, and problem. In which, the ecosystem in BBO corresponds to population in GA, both of which represent the solution set of a problem. Habitat in BBO corresponds to individuals in GA, and they all represent a solution in a problem solution set. HSI in BBO corresponds to fitness in GA, they both represent the objective function of a problem. SIV in BBO corresponds to GA, they all represent variable in a problem [28].

Figure 4

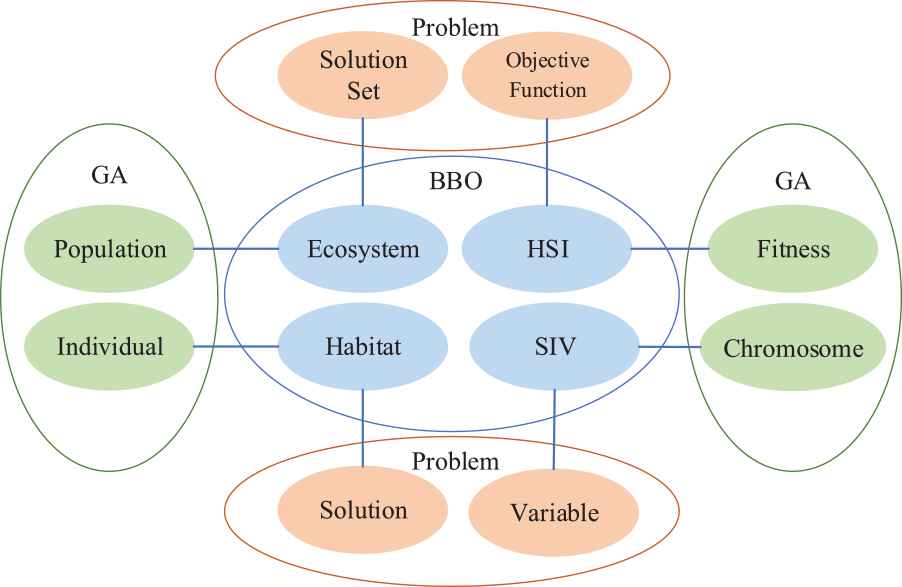
The relationship among genetic algorithm (GA) genetic algorithm genetic algorithm and biogeography-based optimization (BBO) and problem space.

To accurately describe biogeographic models, we will introduce the terms as follows: habitat, where species live and reproduce, to describe candidate solutions to the problem to be solved. Habitat suitability index (HSI), which measures the number of species in a habitat and describes the practicality of a candidate solution. Suitability index variable (SIV), which measures the habitability of a habitat and is used to adjust the practicality of a candidate solution. Among them, migration operation and mutation operation are the main steps of BBO algorithm in optimizing specific problems. At the same time, the introduction of elitism solves the problem of saving better solutions in the process of BBO algorithm. Figure 5 shows the species migration diagram of BBO algorithm.

Figure 5

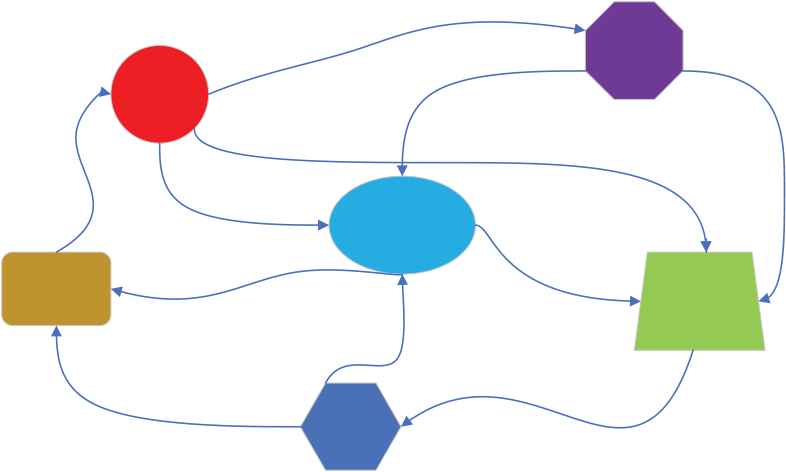
Diagram of biogeography-based optimization (BBO) habitat and migration. (The geometric shapes represent habitats, and the arrows represent migrations)

3.5.2. Migration operation

The migration operation of BBO algorithm mainly depends on the migration operator. Species migrate from habitats with a higher value of HSI to habitats with a lower value of HSI [29]. Therefore, the following formula can be obtained:

λN=T×1−NNmax(20.a)

μN=P×NNmax(20.b)

where λN symbolizes the immigration rate of habitat with N species. μN symbolizes the emigration rate of habitat with N species. T and P represent the maximum rate of immigration and emigration, respectively.N is the number of species in a habitat. Nmax is the maximum number of species in a habitat. Figure 6 illustrates the linear model of population migration.

Figure 6

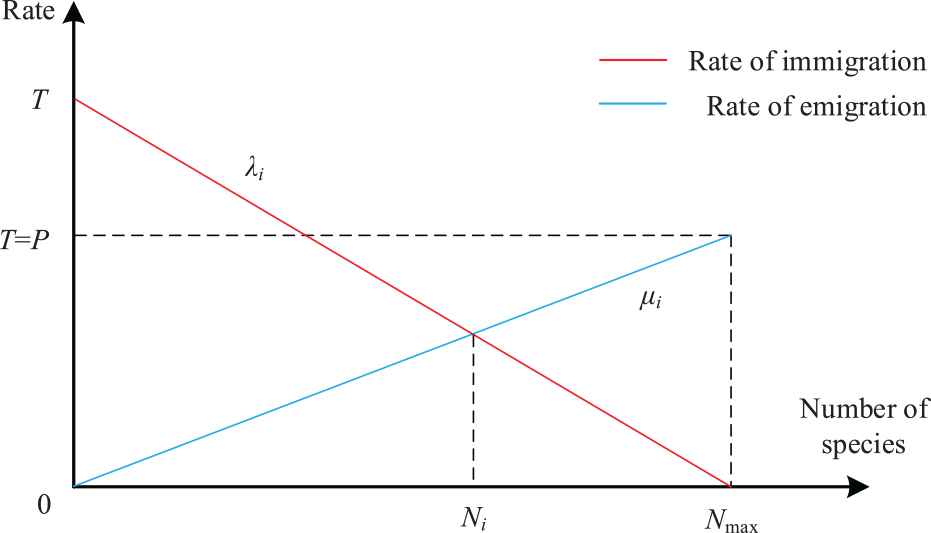
Linear model of population migration.

Considering that the maximum immigration rate P is equal to the maximum emigration rate T, it can be expressed as

λN+μN=P(21.a)

λN∈(0,1],μN∈(0,1](21.b)

3.5.3. Mutation operation

BBO algorithm will select some habitats with low HSI value to perform mutation operation. Habitat optimization is achieved by changing a single SIV to facilitate migration of species. Thus, the number of species in a habitat is closely related to the probability of mutation. This leads to the following update formula:

αN=αmax1−PNPmax(22)

Here, αmax represents the definable maximum mutation rate. αN represents the probability of performing mutation operations on a habitat of N species. Pmax is the maximum probability of species. PN is the probability that the habitat has the number of N species. PN is updated using following equation:

PN←−λN+μNPN+μN+1PN+1N=0−λN+μNPN+λN−1PN−1+μN+1PN+11≤N≤Nmax−1−λN+μNPN+λN−1PN−1N=Nmax(23)

until the algorithm ends. Figure 7 is the schematic diagram of standard BBO algorithm.

Figure 7

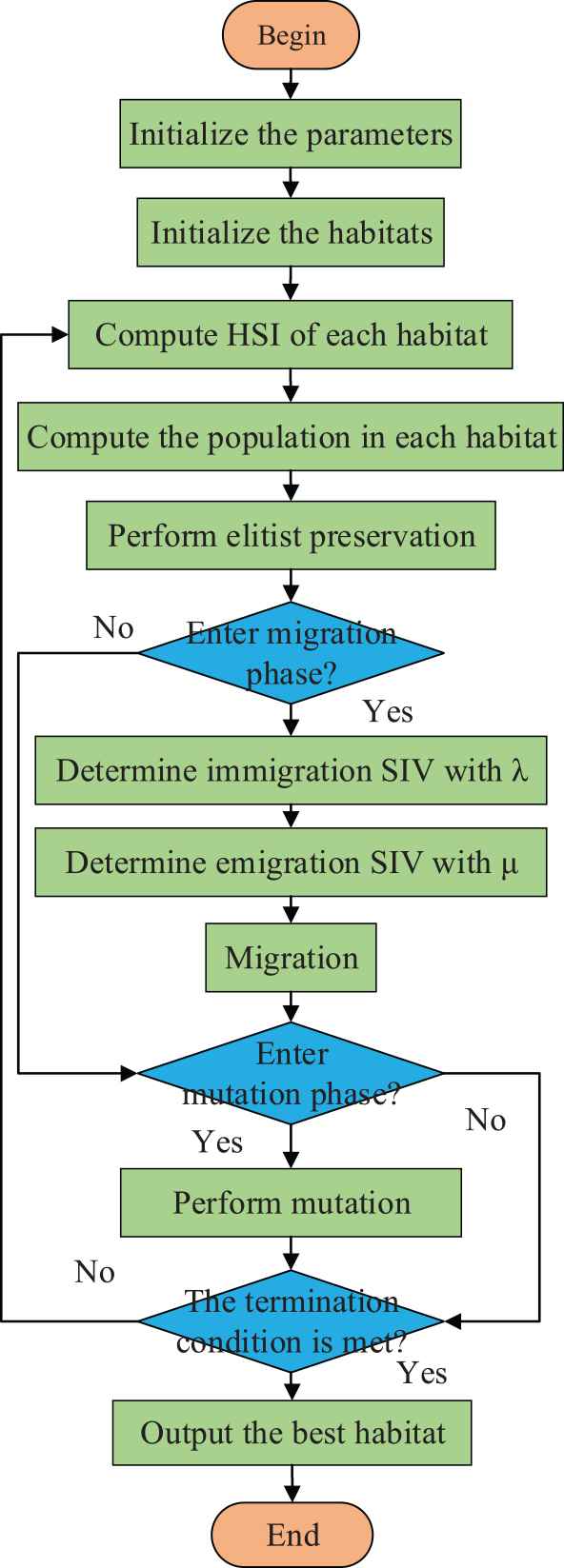
Flowchart of biogeography-based optimization (BBO) method.

3.6. Proposed Three-Segment BBO (3SBBO)

3SBBO can optimize of the RE order, weights and biases simultaneously by combining three-segment encoding strategy with the advantages of BBO, e.g., fast convergence speed, fewer algorithm parameters, and strong global search ability.

3.6.1. Rational of 3SBBO

The standard BBO algorithm optimizes the weights and bias of FNN by performing migration operations and mutation operations. However, we believe that RE order is also an important parameter affecting WRE feature extraction performance under the premise of fixing the number of FNN hidden layer neurons. Therefore, we propose the 3SBBO designed to simultaneously optimize RE order, weights, and bias.

Figure 8 is the flow chart of our method. We will collect chest CT of the subjects and then conduct K-fold cross validation (CV) (K=10 in this paper). The detailed procedures in this 10-trial loop is: (i) The fold k (k=1,2,…K) is selected as the test set and the remaining folds as the training set. Table 2 shows the pseudocode of our 3SBBO algorithm.

Figure 8

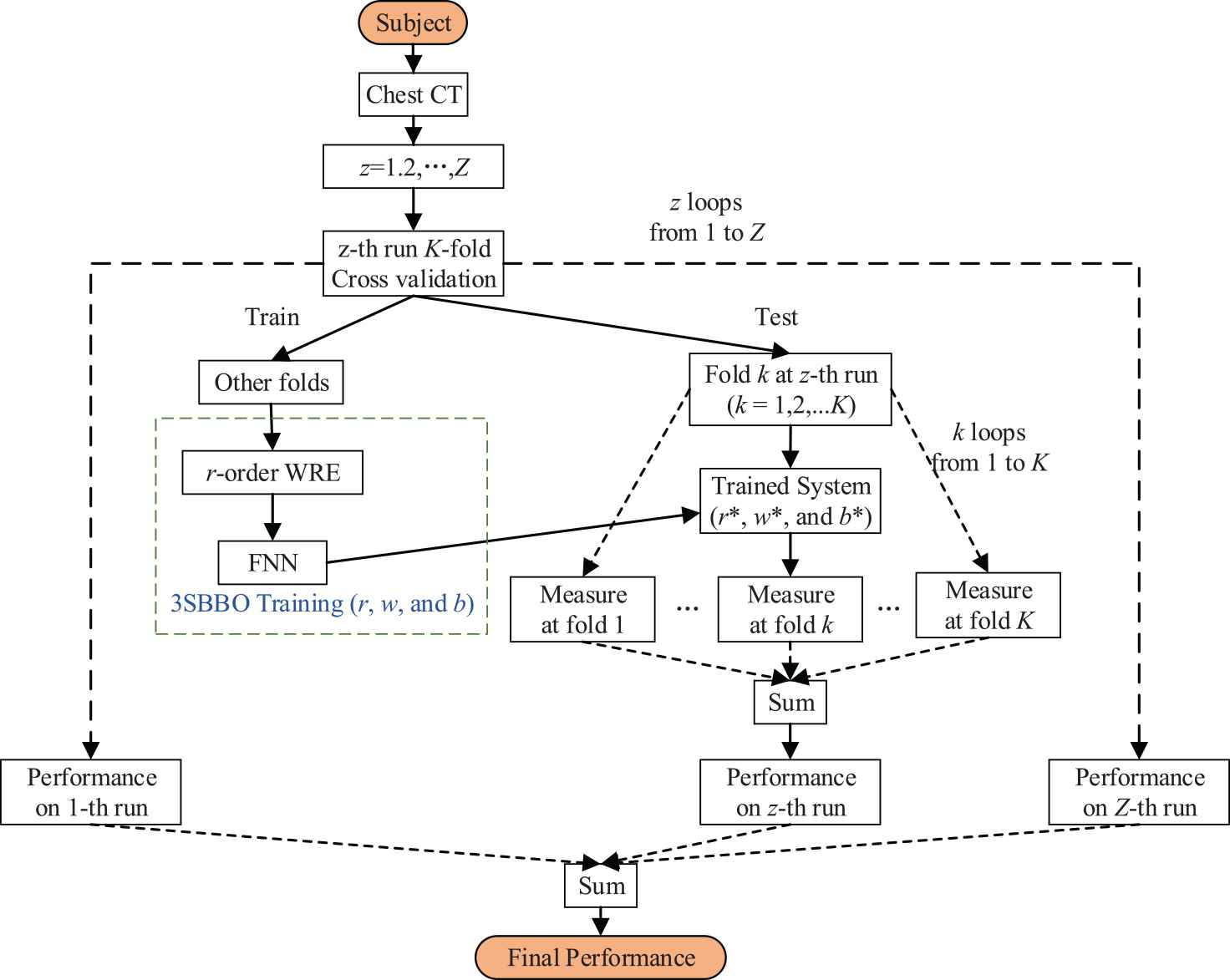
The flowchart of proposed three-segment biogeography-based optimization (3SBBO) method.

Table 2

Pseudocode of three-segment biogeography-based optimization (3SBBO).

On the training set, 3SBBO is used to optimize the RE order, weights, and biases. (ii) The optimized r-order WRE and trained FNN are applied to the test set to get the test results. The loop repeats the above calculation operation K−1 more times (excluding the first trial), and a total of K test results could be obtained. By averaging these K test results, we can get the final classification performance.

3.6.2. Encoding of 3SBBO

To optimize our task, the variable γ can be expressed in a three-segment (3S) way as below:

γ=γr,γW,γb(24)

Here, γr, γW, γb represent the first segment, second segment, and third segment of the optimized candidate. γr represents optimization of REorder. γW represents optimizing the weights and it concludes two subparts (weights of hidden layer γW,H, and weights of hidden output γW,O)

γW=γW,H,γW,O(25)

and γb represents optimizing the biases, which similarly is composed of two subparts (biases of hidden layer γb,H and weights of hidden output γb,O)

γb=γb,H,γb,O(26)

The total population can be written as

γ1,γ2,…,γM(27)

where M is the number of habitats. Figure 9 shows the encoding of habitat and ecosystem.

Figure 9

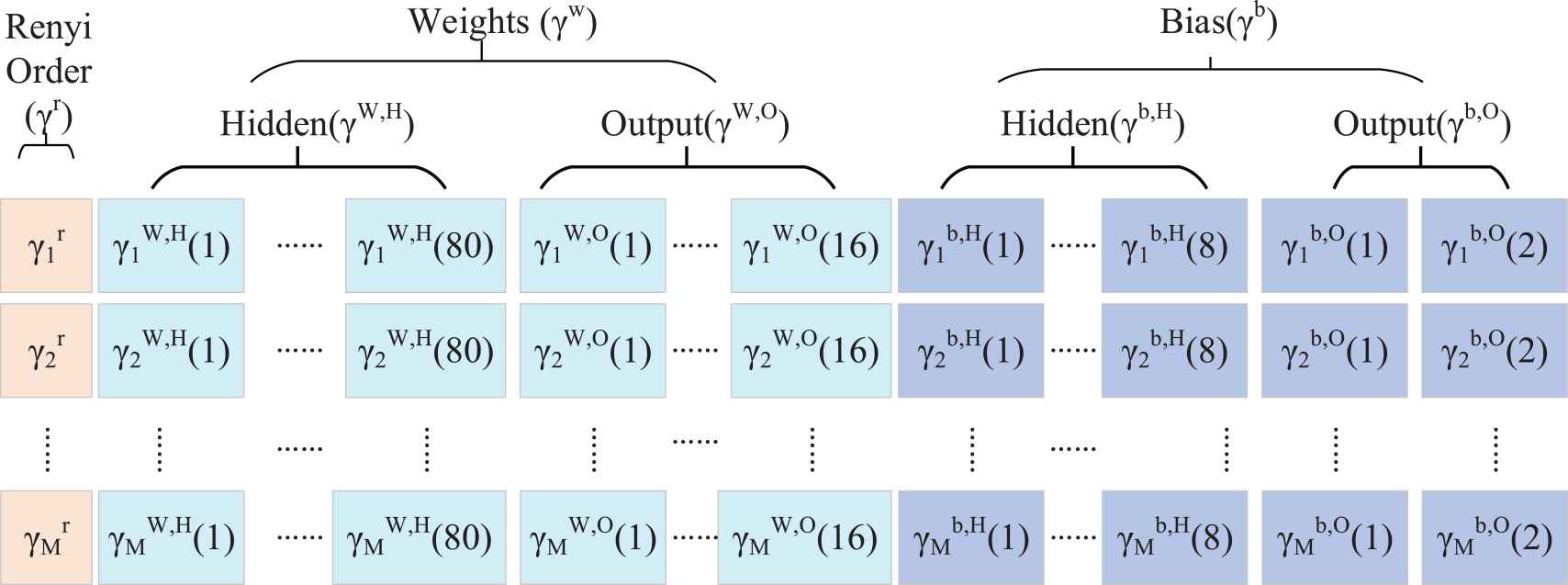
Encoding of habitat and ecosystem.

4. EXPERIMENTAL DESIGN

4.1. 10 Runs of 10-Fold CV

In this paper, in order to prevent overfitting, 10-fold CV is introduced. CV is a strict statistical validation technique widely used in many academic fields, such as harmonic approximation [30], ferromagnetic resonance [31], etc. The specific implementation method is as follows: the experimental dataset is randomly divided into 10 equal parts, numbered from 1 to 10. First, set the fold No.1 as the test set, the remaining folds as the training set. Then set the fold No. 2 as the test set, and the remaining folds as the training set. Take turns to set the fold No. 3 through No. 10 as test set, and set the remaining dataset as training set in each turn. Figure 10 shows an example of one run of 10-fold CV on our dataset of 296 images.

Figure 10

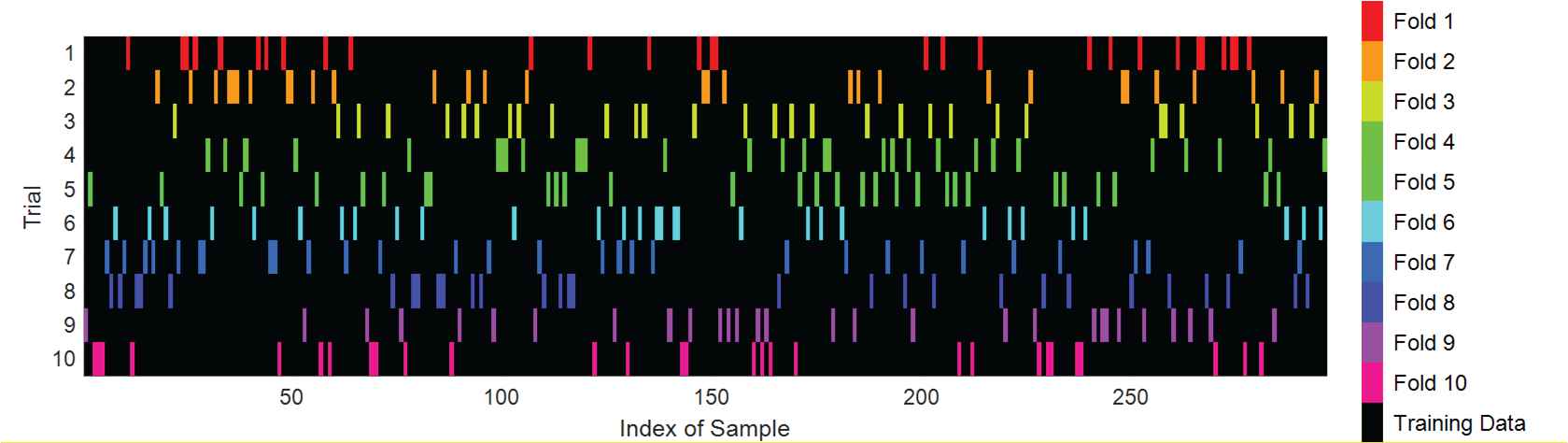
Illustration of one run of 10-fold cross validation.

Finally, the sum value of the test results of the above 10 folds is obtained, so as to evaluate the performance of proposed algorithm. To make a more accurate assessment of the accuracy of algorithm, we will carry out 10-fold CV 10 times.

In this experiment, the deal confusion matrix C of one run of ideal 10-fold CV is shown below, k is the number of folds (k loops from 1 to K) and z is the number of repetitions (z loops from 1 to Z)

Cidealz=∑k=1KCidealk,z=148  0  0148(28.a)

K=10(28.b)

The ideal confusion matrix for 10-fold CV 10 times is

Cideal=∑z=1ZCidealz=1480 0 01480(29.a)

Z=10(29.b)

5. Experiment Results and Discussions

The parameters of this study were set by trial-and-error method and described below. Wavelet decomposition level = 3; Number of hidden heurons = 8; Maximum iterative epochs = 500; Population size = 20; Maximum emigration rate = Maximum immigration rate = 1; Maximum mutation rate = 0.1.

5.1. Wavelet Decomposition

Figure 11 is a sample of CT wavelet decomposition of the lungs of COVID-19 patients and healthy subjects, where, (b) and (d) are the 3-level decomposition of (a) and (c), respectively. We can clearly see that in the CT images of the lungs of COVID-19 patients, the shape of both lungs on tends to be round, and the apex of the upper lobe of the right lung has visible patchy ground glass shadow, which is in sharp contrast to the CT images of the lungs of healthy subjects. At the same time, this phenomenon can be observed more clearly in the picture after the 3-level decomposition.

Figure 11

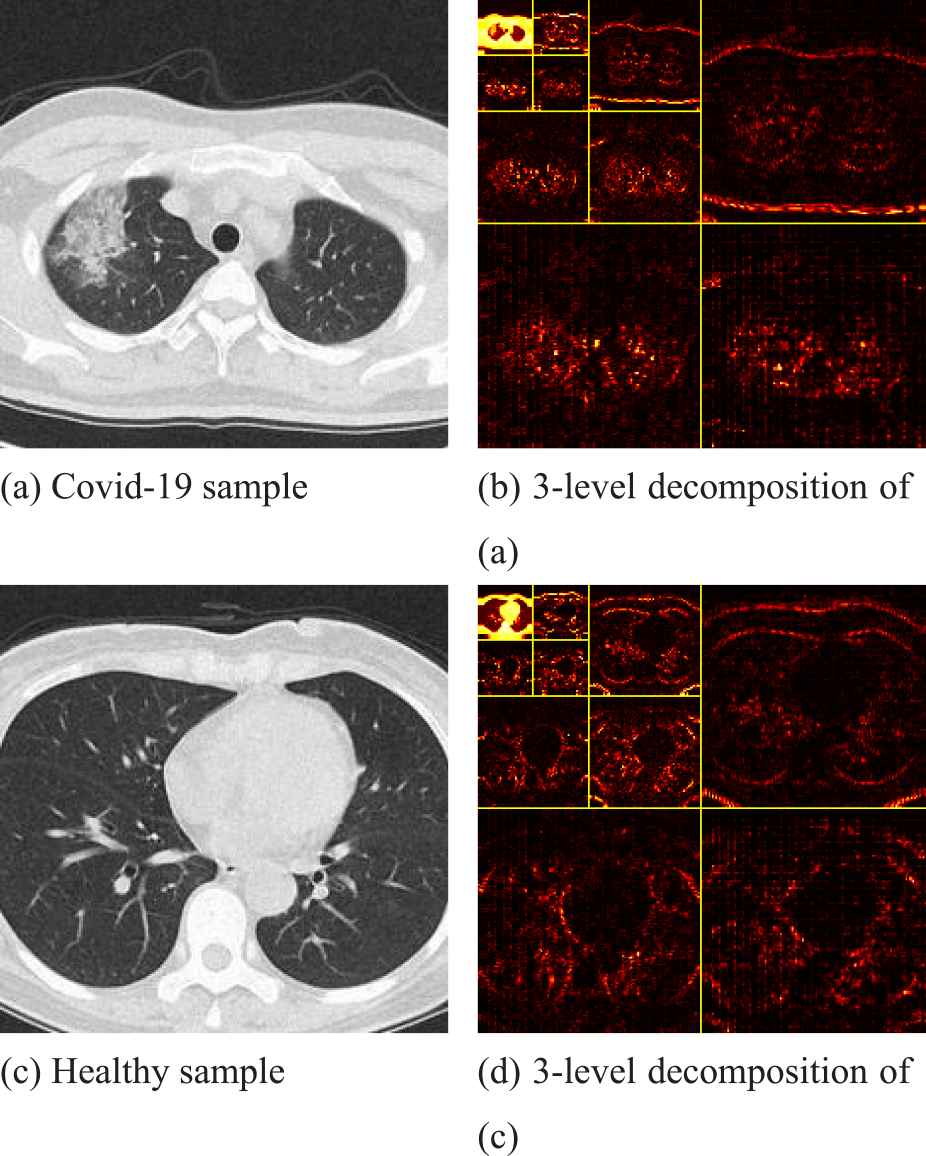
Two samples of wavelet decomposition.

5.3. Comparison to State-of-the-Art Algorithms

We compared our 3SBBO algorithm with state-of-the-art approaches: RBFNN [5], KELM [6], ELMBA [7]. As shown in Table 4 and Figure 12, RBFNN, KELM and ELMBA use hold-out validation and our method uses 10×10-fold CV. In the detection of precision, accuracy and F1 for COVID-19, the best is 3SBBO (Ours), the second is RBFNN, the third is ELMBA, and the last is KELM. In the detection of sensitive for COVID-19, the best is 3SBBO (Ours), the second is RBFNN, the third is KELM, and the last is ELMBA. In the detection of specific for COVID-19, the best is 3SBBO (Ours), the second is ELMBA, the third is RBFNN, and the last is KELM. Furthermore, the MCC value of 3SBBO is 72.42±5.55%. To sum up, 3SBBO (Ours) presents better performance than the current method in the detection of COVID-19.

Appr	VD	Sen	Spc	Prc	Acc	F1	MCC
RBFNN [5]	HO	65.91	75.00	72.50	70.45	69.05	–
KELM [6]	HO	56.82	61.36	59.52	59.09	58.14	–
ELMBA [7]	HO	55.00±2.58	76.36±2.44	69.97±2.44	65.68±1.92	61.56±2.25	–
3SBBO (Ours)	10x10 fold CV	86.40±3.00	85.81±3.14	86.14±3.03	86.12±2.75	86.16±2.77	72.42±5.55

(- means not available, Appr means approach, VD means validation, HO means hold-out, CV means cross validation)

Sen, Sensitivity; Spc, Specificity; Prc, Precision; Acc, Accuracy; MCC, Matthews correlation coefficient.

Table 4

Comparison of state-of-the-art approaches in detecting COVID-19.

Figure 12

Bar plot of comparison results.

6. Conclusions

In this paper, we propose a computer vision-based diagnosis method based on WRE and the proposed 3SBBO. The method consists of three parts: WRE as feature extractor, FNN as classifier, and 3SBBO algorithm as optimizer. As can be seen through the experiment, after 10 times 10-fold CV, the MCC value of our method is 72.42±5.55%, and the performance of other indicators is also better than the other three state-of-the-art approaches (See Section 5.3). Compared with the existing global optimization methods (See Section 5.2), the 3SBBO algorithm proposed in this paper has better performance than other methods.

The disadvantages of this proposed smart COVID-19 diagnosis system are 2-fold: firstly, the WRE was extracted, we will attempt to test other effective features. Secondly, we will try to improve BBO, such as speed up the convergence speed of BBO algorithm and get a better global optimal solution.

In future studies, based on the differences between chest CT of COVID-19 patients and common pneumonia patients, the chest CT of COVID-19 patients where mesh shadow is more common in the lungs and boundaries are clearer. And chest CT of common pneumonia patients, where nodules of internal consolidation and thickening of bronchial wall are more common, with blurred boundaries. We will conduct a classification study of chest CT diagnosis of COVID-19 patients and common pneumonia patients based on computer vision. Second, we will develop a classifier based on multisource data, so that it can be applied to face recognition, alcoholism detection, and spectrum data. Third, we will try to collect more data and test the deep learning method.

CONFLICTS OF INTEREST

The authors declare that there is no conflict of interest.

AUTHORS' CONTRIBUTIONS

Shuihua Wang proposed the idea, Xiaosheng Wu and Chaosheng Tang implemented the algorithms. Xin Zhang drafted the paper and checked the experiment result. Shuihua Wang and Yudong Zhang drafted the paper and gave critical revisions. All authors approved the submission of the work.

ACKNOWLEDGMENTS

This paper was partially supported by Henan Key Research and Development Project (182102310629); Guangxi Key Laboratory of Trusted Software (kx201901); Royal Society International Exchanges Cost Share Award, UK (RP202G0230); Medical Research Council Confidence in Concept Award, UK (MC_PC_17171); Hope Foundation for Cancer Research, UK (RM60G0680); Fundamental Research Funds for the Central Universities (CDLS-2020-03); Key Laboratory of Child Development and Learning Science (Southeast University), Ministry of Education.