Face Inpainting with Deep Generative Models
- DOI
- 10.2991/ijcis.d.191016.003How to use a DOI?
- Keywords
- Face inpainting; Structural loss; Semantic inpainting; Deep generative models; GANs
- Abstract
Semantic face inpainting from corrupted images is a challenging problem in computer vision and has many practical applications. Different from well-studied nature image inpainting, the face inpainting task often needs to fill pixels semantically into a missing region based on the available visual data. In this paper, we propose a new face inpainting algorithm based on deep generative models, which increases the structural loss constraint in the image generation model to ensure that the generated image has a structure as similar as possible to the face image to be repaired. At the same time, different weights are calculated in the corrupted image to enforce edge consistency at the repair boundary. Experiments on different face data sets and qualitative and quantitative analyses demonstrate that our algorithm is capable of generating visually pleasing face completions.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
The goal of face inpainting, also known as face completion, is to produce a more legible and visually realistic face image from an image with a masked region or that has missing content. As faces play the most substantial role in depicting human characters [1], face inpainting becomes the basis of face verification and identification when an occlusion or damage exists in the facial part of an image. These applications make face completion very important in today's computer vision. Face images have obvious high-level semantics that include many special objects. For face images missing unique pattern objects, the original images may not be restored successfully using traditional inpainting methods. Figure 1 shows how the traditional popular TV [2] and PatchMatch [3] methods fail at face inpainting. The TV method is a total variation-based approach, while PatchMatch is a content aware fill method implemented in Adobe Photoshop.

Face inpainting results obtained by TV, PatchMatch, DIP and the proposed method.
Recently, deep learning neural networks have been extensively studied and have demonstrated their capability to capture abstract information contained in images at high resolution [4]. One of the feedforward neural networks, the convolutional neural network (CNN) [5], is effective because each of its artificial neurons responds only to some of the neurons connected to it, making the application of deep learning neural networks in large-scale image processing possible by avoiding the over-fitting phenomenon. On the other hand, extensive research [6–10] on generative adversarial networks (GANs) [11] has shown that the visual effect of generated images can be enhanced by adversarial training. Based on this research background, CNN-based image completion methods with adversarial training strategies have already significantly improved image completion performance [12–14].
The early proposed deep learning-based semantic image restoration methods were implemented by training an encoder–decoder CNN (a context encoder) [12] which is closely related to the self-encoder [15–17], to predict the unavailable content in an inpainting image. That is, the network is trained to fill in an image's unknown content based on the known content. However, the context encoder considers the structure of missing regions only during training but not during inference, which will inevitably cause ambiguity and error in the results. Based on the context encoder network, the authors in [18] added a local adversarial loss and a semantic parsing loss to train the model to ensure pixel faithfulness and local content consistency, but ambiguity is still present in the results when missing regions have arbitrary shapes [13].
When considering GANs, if some constraints can be provided in the generating process, such as forcing the generated image to be similar enough to the corresponding part of the known region of the inpainting image, then we can find the best matching latent space representation closest to the natural image manifold without specifying any explicit distance based loss. Then, the image can be restored by fusing the image generated by the GAN and the known region of the inpainting image. In other words, the image can be completed by blending the image generated by the GAN and the known regions of the inpainting image [13] (known as “DIP”, Image Inpainting with Deep Generative Models). In spite of this success, some challenges still exist in face inpainting. Firstly, human faces have a definite geometric distribution, and hence any face inpainting method based on deep learning must consider the geometric structure loss in the process of restoration. Secondly, coherence is very important in face inpainting and must be considered in the process of face image completion.
To address these two concerns, this study develops a face inpainting network that promotes content continuity and structural consistency. On the one hand, we apply the experience gained from traditional image inpainting methods in our method. That is, more attention should be paid to the continuity of the inpainted region boundary, so we increase the weights for content loss and structural loss at the boundary portions of the region to be repaired, which can ensure the continuity of content in the repair results. On the other hand, for the face completion problem, the rationality of the overall structure of the repair results is very important. Accordingly, we add the structural loss in the generation process to ensure that the generated image has a structure that is as similar as possible to the face image to be repaired. The procedure of the proposed method is as follows. In the first stage, a deep generative model is trained using face samples. In the second stage, a face image is iteratively generated that is “closest” to the input face image. For the iteratively generated image with a combination of adversarial loss, content loss and structural loss, the loss weights near the repair border regions are increased. In the last stage, the image blending method is used to fuse the known region content of the corrupted image and the corresponding generated content to the unavailable region in the original damaged face image. We evaluate our method on the CelebA and SiblingsDB datasets with different shapes of the missing area in an image. Results demonstrate that compared to the traditional methods, our method can implement semantic restoration, and compared to the benchmark DIP method, our method can obtain more realistic and reasonable results (as shown in Figure 1).
The main technical contributions of the proposed method are summarized as follows:
A novel network is developed to complete semantic face image inpainting from masked face images. This method generates samples that are more similar to the inpainting face image by adding structural loss and applying an adaptive weight strategy to the face generation model.
A novel structural loss measurement method based on structural similarity index (SSIM) values is introduced, which includes the SSIM value calculation method for the image to be repaired and the generated image, and a normalization method of these SSIM values is used to define the structural loss.
Our method guarantees the consistency of the repaired boundary in the repaired result by implementing an adaptive weight strategy, that is, larger weight values are applied to the structure and content loss of pixels closer to the repair boundary.
2. RELATED WORK
2.1. Image Generation
Owing to the good high-level semantic capture capabilities of the variational auto-encoder (VAE) [19] and GAN, a large number of image generation methods [12,20,21] have been proposed recently. The VAE methods usually use the pixel-wise L2 distance (Euclidean) loss between the generated image and original image to train the network. However, because the Euclidean distance is used to minimize the average value of the difference between all input and output pixels, it will inevitably cause ambiguity. By contrast, GANs are known to generate sharper images compared to VAE. Especially for a particular type of image, GANs can generate samples that are difficult to distinguish between true and false [7]. The DIP method [13] is a semantic face inpainting algorithm based on this idea. In the DIP method, image inpainting is performed by adding the content loss between the image's available information and the corresponding generative samples to constrain the iterative generation of the GAN; specifically, the L1-norm is used to define the content loss. Owing to its very good repair results, the DIP method has become a contemporary benchmark method. In [21], the authors proposed an improved DIP method. They present a semantically conditioned GAN, which increases the conditional information to constrain the GAN, to map a latent representation to a point in the image manifold based on the underlying pose and semantics of the scene. This method has been successfully applied to face restoration in video sequences.
Our method also represents an improvement to the DIP method. Unlike [21], we do not use the facial semantic map as a condition for the face generation network and instead emphasize the importance of the facial structure for face completion by increasing the structure loss weight in the face generation network directly. In addition, we focus on the repair of a single image, while the method in [21] extracts the facial semantic map based on a video sequence. However, because these methods are based on image generation, they are all based on deep convolutional GAN (DCGAN), which is a network that adds a deep convolutional network structure to GAN. Technical details follow.
GANs consist of two separate neural networks, where one of the neural networks is referred to as “
DCGAN [7] is widely used in image generation applications because it can generate much sharper images. We use a pre-trained DCGAN, which greatly improves the stability of GAN training, to generate the face in our proposed face inpainting network. The DCGAN architecture is described in Figure 2, where the discriminator network
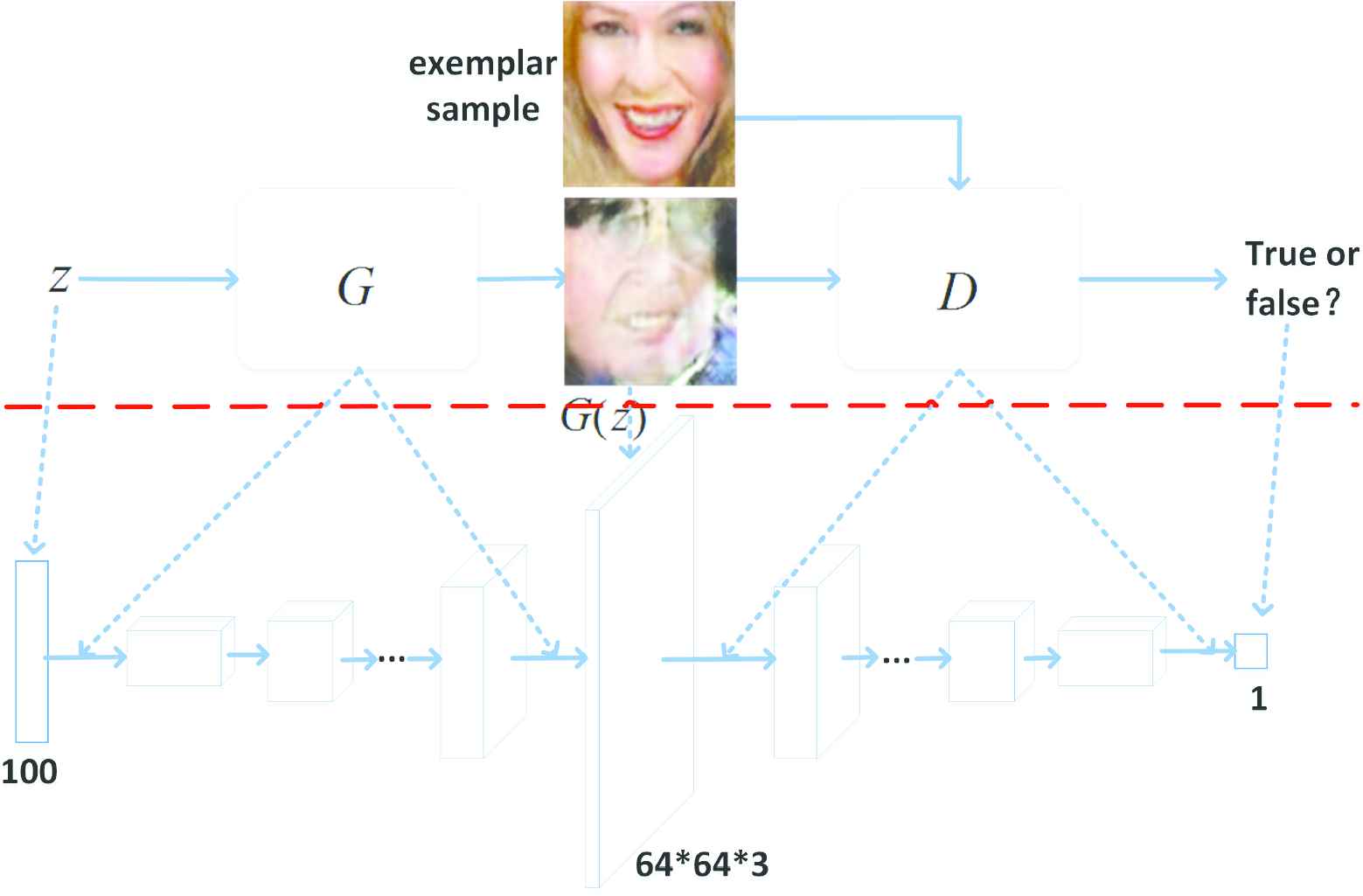
Deep convolutional generative adversarial network (DCGAN) framework overview. The figure consists of two parts (divided by a red dotted line), the upper part is a schematic diagram of DCGAN training, and the lower part is the overall architecture of DCGAN.
2.2. Image Loss Measurement
Although DCGAN can generate a sample image that appears to be a real image, DCGAN cannot be directly applied to the image inpainting task. This is mainly because of the fact that the image generated by DCGAN may not be related at all to the provided corrupted image. Therefore, an effective method for applying DCGAN to image inpainting is to constrain the image generation of DCGAN through the information in the image to be repaired, so that the generated image is sufficiently similar to the image to be repaired. To accomplish this, the measurement of the similarity between the generated image and the provided corrupted image must be considered.
Image similarity measurement methods include image content-based methods (e.g. sum of squared differences (SSD)), image pixel statistics-based methods (e.g. variation of square error (VSE)), image structure-based methods (e.g. the SSIM [29]), and information theory-based methods, such as normalized cross-correlation, Kullback–Leibler(K–L) divergence, and others. For example, the PatchMatch method uses the L2 distance to measure image patch matching. Considering that pixel-wise metrics tend to reflect the overall difference between the two images, this type of measurement does not involve the direct correlation between images. It is well known that face images have clear structural correlations. According to the well-known visual psychology theory (Gestalt theory), the human eye is particularly sensitive to structural information in images. Therefore, in the generation process of the proposed method, in addition to using the content loss used in DIP to measure the face difference, an image difference metric based on the structural information of the face is added. Specifically, we adopt SSIM, which can measure image similarity based on brightness, contrast and structure, to measure the structural loss of the generated face image.
SSIM was proposed by the Laboratory for Image and Video Engineering at the University of Texas at Austin [29]. Given two images
In terms of the implementation of image structural similarity theory, SSIM defines structural similarity from the perspective of image composition and independent brightness and contrast. In this fashion, SSIM can well reflect the differences in the structural properties of objects in different images.
3. METHOD
3.1. Network Architecture
For the semantic image inpainting methods based on deep generative models, the issue of image restoration is not considered at the network training stage. That is, adversarial training takes place in GAN using non-damaged real samples and generated samples, so that “
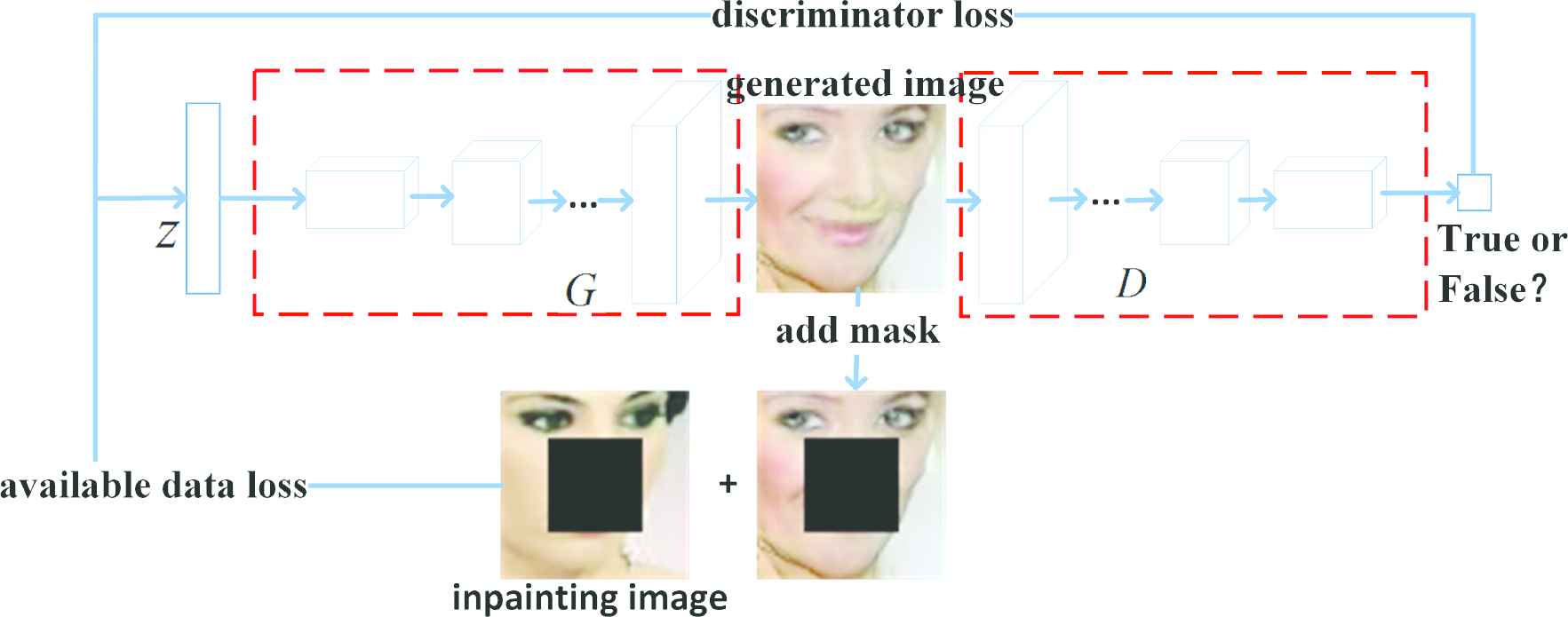
Framework for image inpainting based on deep generative models. The face image is iteratively generated by the DCGAN network with face generation capability, and finally the face image most similar to the known portion of the face image to be repaired can be generated.
According to the framework of Figure 3, the image inpainting process is to generate a new sample
3.2. Objective Function
We first introduce the discriminator loss
By using
Regarding the reconstruction loss
To set reasonable weight values, an effective way is to normalize the various loss values. For example, although SSIM can well describe the structural similarity between two images, its range of values is 0 to 1; when the two images have greater similarity, its value is larger. The
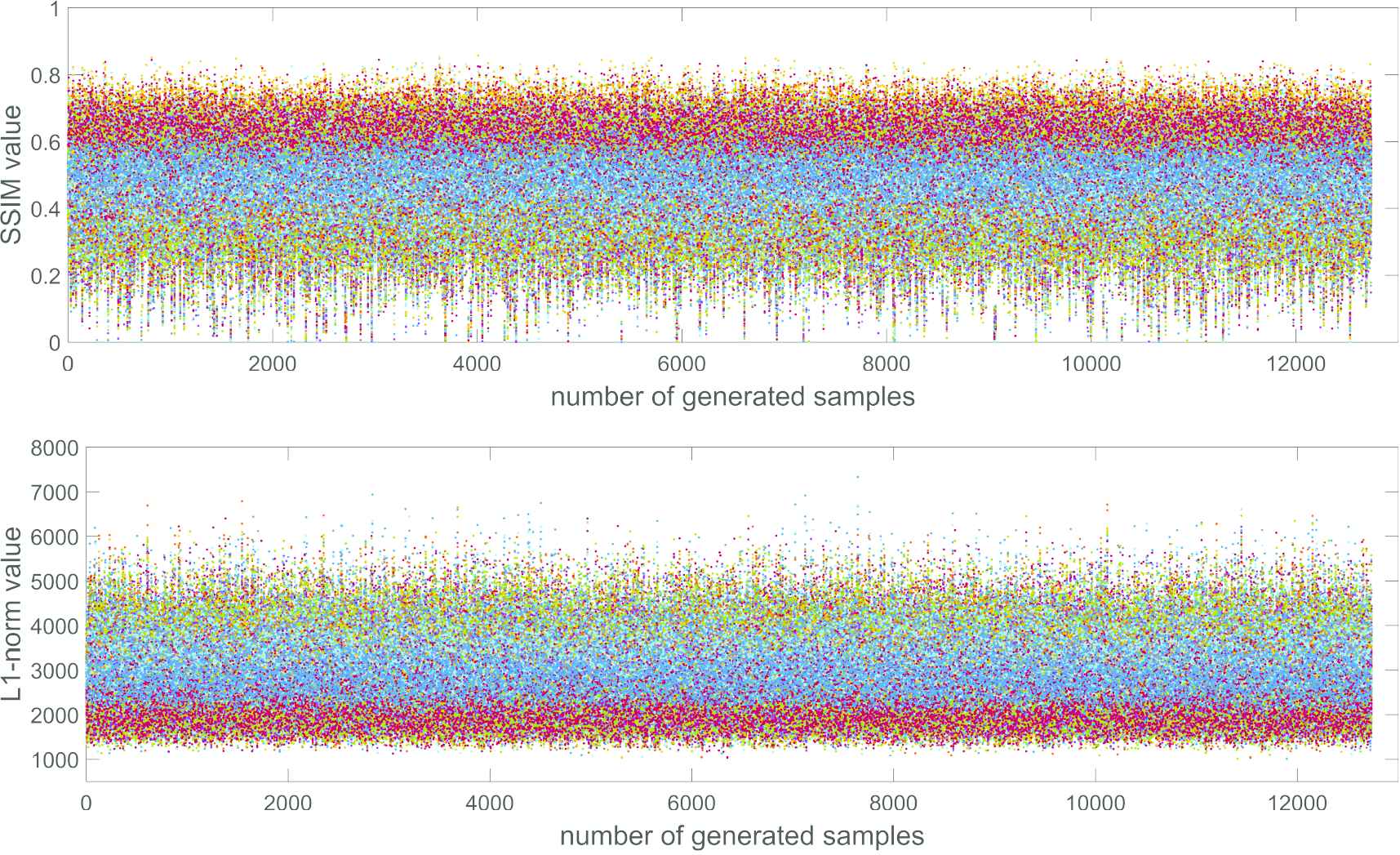
Scatter plots of the structural similarity index (SSIM) values and -norm values between generated samples and test samples.
We calculate the mean
In the equations,
In addition to the
To achieve this goal, we propose a weighted loss matrix
Through the calculation of Formula (7), the weight values of the pixels far from the repair contours (where the distance is greater than
Thus, for each input corrupted face image
Figure 5 shows the results for image inpainting using each of the three losses independently. Figure 5(c) shows that the inpainted regions in the results using only the

Face image inpainting results using only loss constraints, respectively.
3.3. Blending Results
By using a back-propagation algorithm based on the total loss of
For an input corrupted image
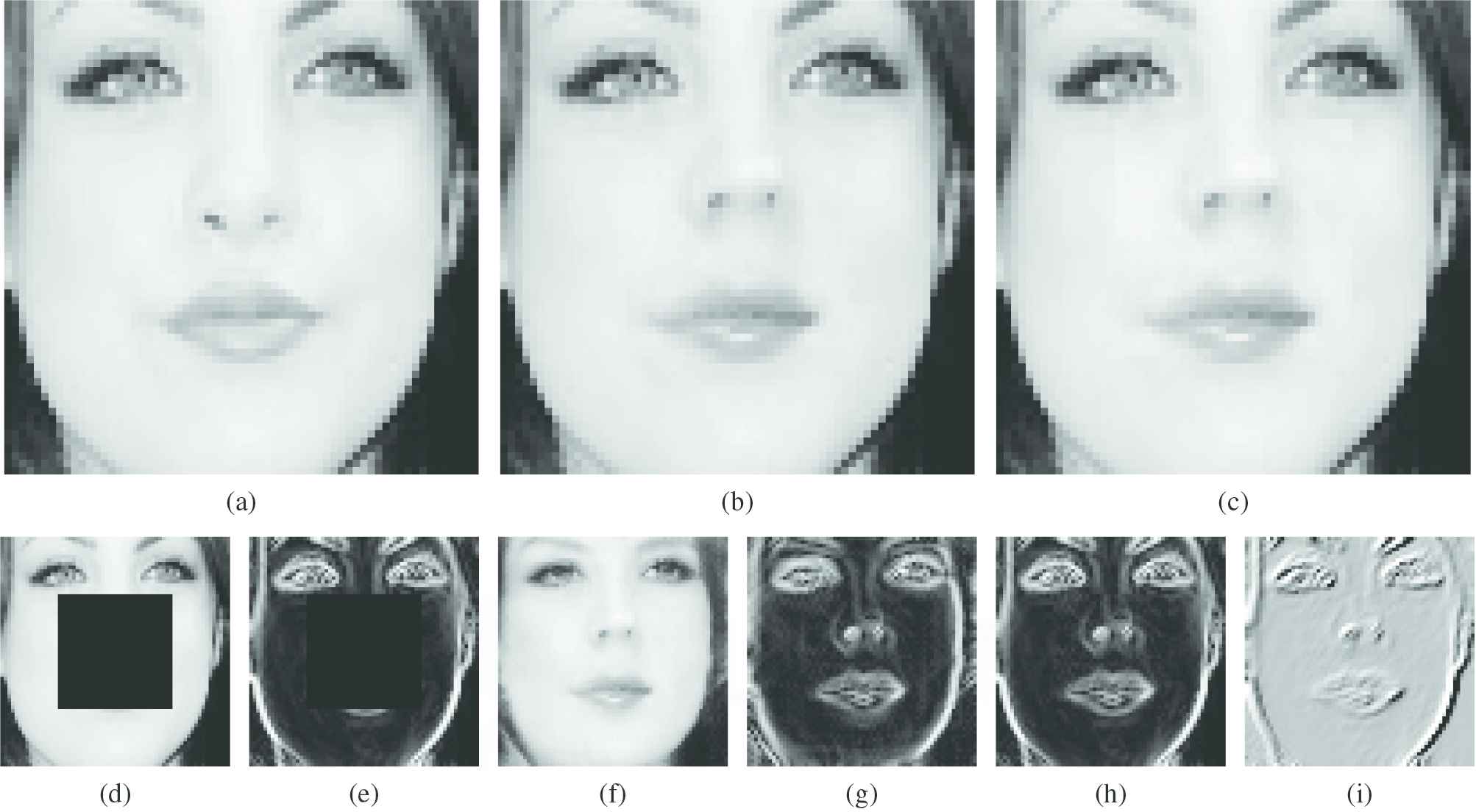
Image blending processing illustration; (a) original image; (b) inpainting result with blending process; (c) inpainting result using the direct stitching method; (d) the masked input image; (e) the gradient field of (d); (f) iterative generated sample image; (g) the gradient field of (f); (h) merged gradient field by combining (e) and (g); and (i) divergence of the merged gradient field.

Comparison of results between inpainting with and without blending.
3.4. Implementation Details
To generate sample images which are very close to the input face image, we make full use of the available information in the input image to restrain the generation process of the deep generative models (
4. EXPERIMENTAL RESULTS
We carry out extensive experiments to demonstrate the capabilities of our proposed method compared to DIP, the state-of-the-art method for semantic face inpainting. Specifically, it includes various standard mask repair comparison experiments, arbitrarily masked face image repair comparison experiments, different face database comparison experiments, and a large number of pixel loss completion experiments.
4.1. Qualitative Analysis
In order to qualitatively analyze the performance of the proposed method, we compare the method with the DIP method. Figure 8 shows the repair results of the DIP method and our method in the case of center-masked images. Figure 9 shows the repair results for various standard masked images, and Figure 10 shows the repair results for arbitrarily masked face images.
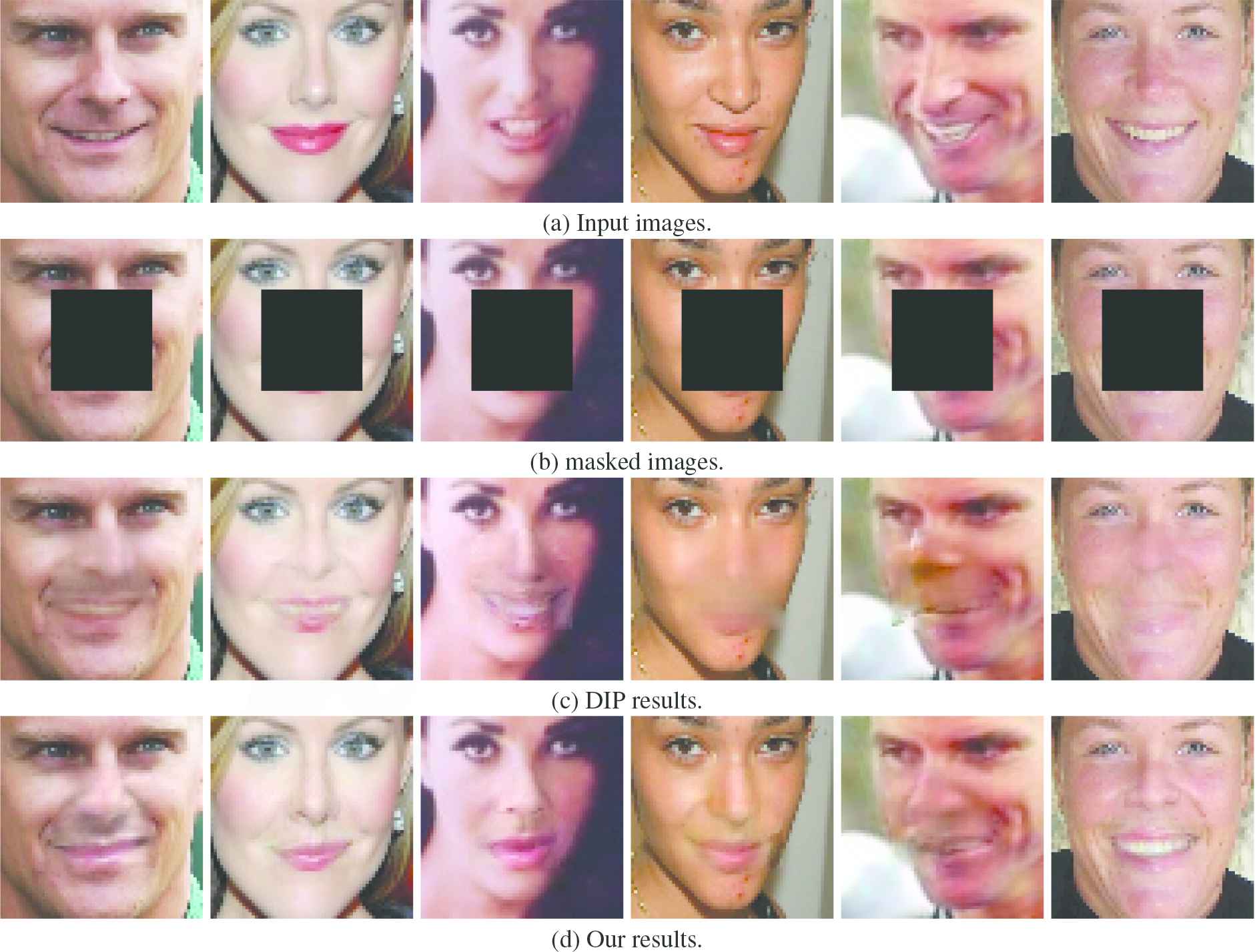
Comparison between DIP method and our method for center-masked images.

Comparison between DIP method and our method for standard masked images.
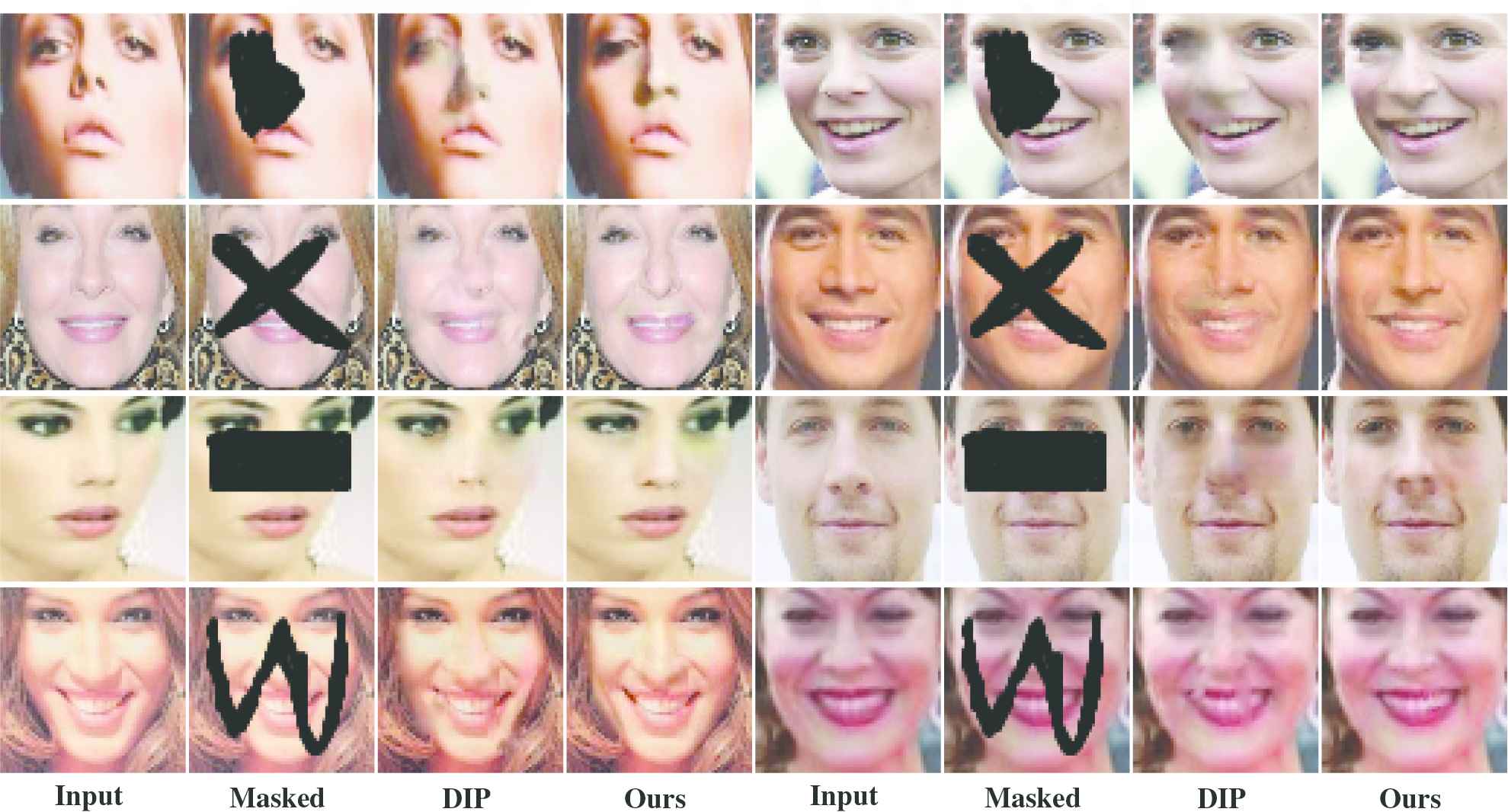
Comparison between DIP method and our method for arbitrarily masked images.
In the six groups of experimental results given in Figure 8, our method achieved better repair results than the DIP method. There are richer face structures and more coherent edges in the proposed method; these properties make the overall repair results more reasonable. In Figure 9, except for the first group of experiments, which repair the upper half of the whole face image, the two methods are not ideal, while the other experimental results using the proposed method achieve better results. In addition to the advantages shown in Figure 8, more consistent facial skin is achieved in our results, and some experimental results have achieved amazing results in which it is difficult to find the repair traces to human eyes. In Figure 10, four different arbitrarily masked inpainting results are shown, and compared with the original images, there are obvious blurred marks in the results using DIP, and unique objects in the face images are more obvious(as shown by the results in the first line).
The effectiveness of the proposed method is verified by qualitative analysis through the three experiments and the results shown in Figures 8–10. The experimental results demonstrate that the final restoration results are more reasonable when the structural loss and adaptive weight strategy are applied.
4.2. Quantitative Analysis
To further verify the effectiveness of the proposed method, we compare the experimental results obtained by randomly discarding
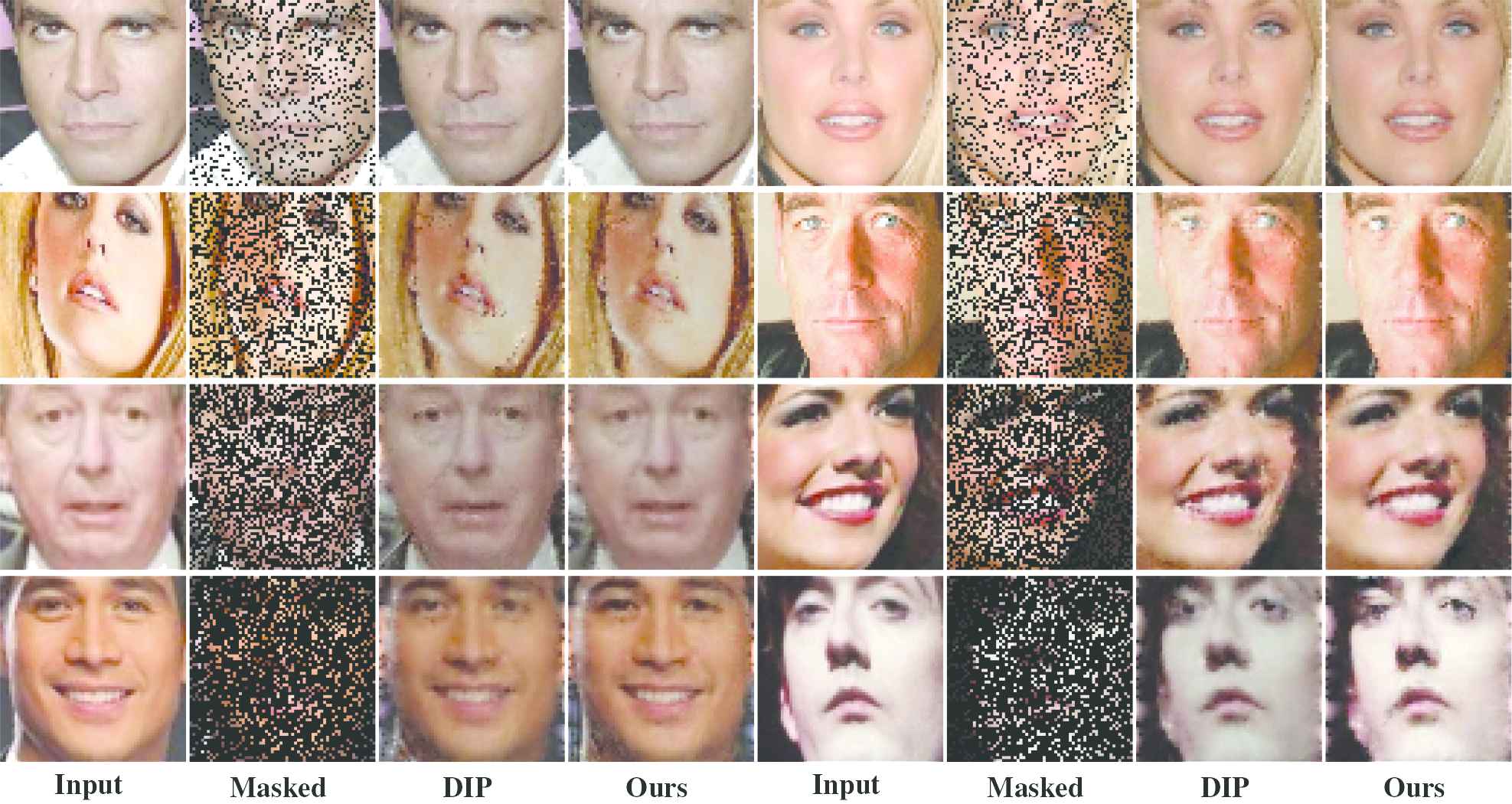
Comparison between DIP method and our method when randomly discarding of the pixels in an image.
| DIP |
Ours |
|||
|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | |
| 20% | 19.8658 | 0.9517 | 20.0649 | 0.9533 |
| 40% | 19.0177 | 0.8975 | 19.9802 | 0.9089 |
| 60% | 18.2592 | 0.8547 | 19.8783 | 0.8892 |
| 80% | 15.7974 | 0.7823 | 19.7447 | 0.8461 |
PSNR values (dB) and SSIM values comparison between DIP and our method based on different proportions of missing pixels.
4.3. Limitations
All of the above experiments are based on the CelebA data set, and the test set is also from CelebA. On the trained network, we therefore use the data from other data sets to carry out further experiments. Figures 12 and 13 show the experimental results when using images from the SiblingsDB data set, and Figure 14 shows the repair results of the Asian face data set.

Comparison between DIP method and our method for images from SiblingsDB with center mask.
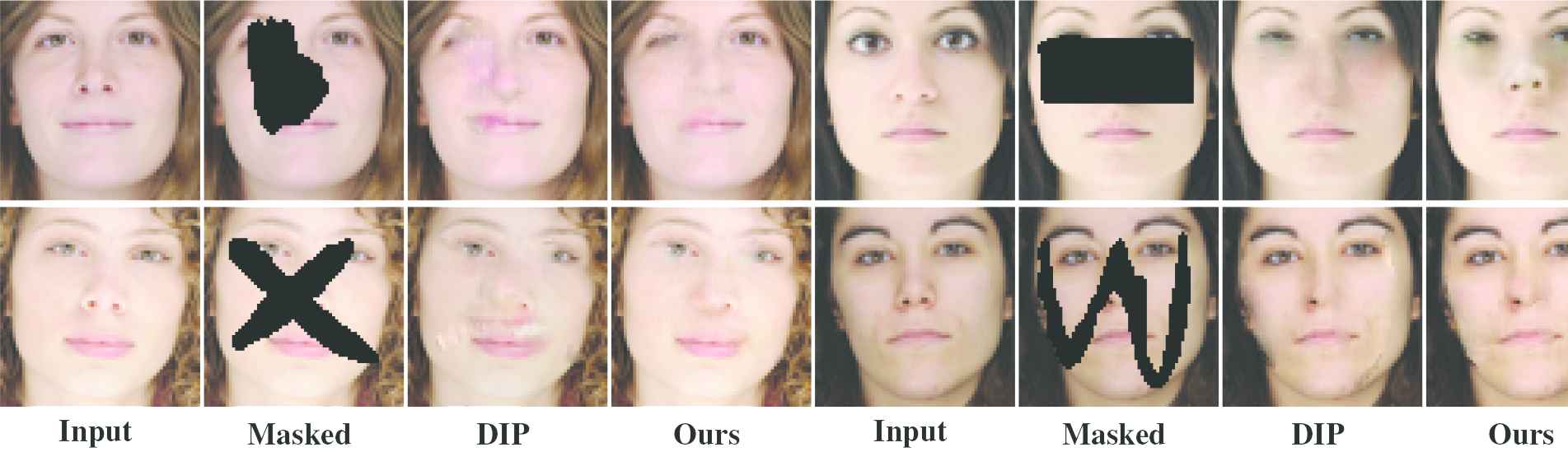
Comparison between the DIP method and our method on SiblingsDB images with arbitrary masks.

Comparison between the DIP method and our method on Asian face images with different masks.
Although our method is capable of obtaining semantically pleasing inpainting results, even on images not used to train the network, it has some limitations. Through the results shown in Figures 12–14, we can find similar failure cases for both DIP and our method. This is because the CelebA data set images are roughly cropped and aligned, while the other data sets are not processed in this manner.
The generation model used in all experiments was DCGAN trained using images from the CelebA dataset, and it is difficult to obtain good results for face images that are not rich in the data set. As shown in Figures 14, the results for the two methods on Asian face images are unsatisfactory.
5. CONCLUSION
In this paper, we apply the experience gained from traditional image inpainting methods to semantic face inpainting based on deep generative models, and through many experiments, the proposed method is proven effective for face inpainting. Compared with traditional image inpainting methods, the proposed method can achieve semantic face completion and its advantages are easily discerned. Compared with the DIP benchmark method proposed recently for semantic face inpainting, the proposed method can enhance content continuity and structural consistency and yield more reasonable inpainted results.
Although we have made some progress in face inpainting, there remains room for further improvement, and we propose the following promising directions for future work.
Standard face model and corresponding representation loss function: The importance of a face's structural information for face inpainting has been demonstrated in this paper, and it is well known that the standard face model is a basic feature of a face's structure [32]. How to obtain the standard face model of the corrupted face image and represent the obtained result as a loss function will be a very valuable research contribution [33].
Symmetric feature and corresponding representation loss function: Another basic feature of the face structure is symmetry [34], which is also a high-level semantic feature of the face. It is highly desirable to be able to represent and apply face symmetry feature(s) to face inpainting effectively.
High-resolution face inpainting and synthesis: Notwithstanding GANs and other models that have greatly improved the quality of face completion, high-resolution face inpainting remains an open problem [35]. A synthesis approach may be an effective way to solve this problem [36].
In the future, we hope that more applications based on face image inpainting will be developed and applied in real life.
CONFLICT OF INTEREST
The authors declare that there are no conflicts of interest regarding the publication of this paper.
ACKNOWLEDGMENTS
This work is supported by the project of National Natural Science Foundation of China (11603016), Key Scientific Research Foundation Project of Southwest Forestry University (111827) and the project of Scientific Research Foundation of Yunnan Police Officer College (19A010).
REFERENCES
Cite this article
TY - JOUR AU - Zhenping Qiang AU - Libo He AU - Qinghui Zhang AU - Junqiu Li PY - 2019 DA - 2019/10/25 TI - Face Inpainting with Deep Generative Models JO - International Journal of Computational Intelligence Systems SP - 1232 EP - 1244 VL - 12 IS - 2 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.191016.003 DO - 10.2991/ijcis.d.191016.003 ID - Qiang2019 ER -
