The life and times of Donald A. McDonald
- DOI
- 10.1016/j.artres.2007.08.002How to use a DOI?
- Keywords
- Pulsatile pressure and flow waves; Fourier analysis; Input impedance; Characteristic impedance; Arterial stiffness; Wave reflections; Pressure gradient
- Abstract
Donald A. McDonald (1917–1973) was a pioneer in hemodynamics. He was Oxford educated and served on the faculty of Universities in both Great Britain and the USA. The problems that were the main theme of his text Blood Flow in Arteries published in 1960 were those concerned with pulsatile blood flow and the associated pulsatile pressure changes. At that time pulsatile flow of liquids had received little attention from scientists compared with the tremendous volume of work on steady flow. Quite apart from the far from easy solution of the characteristics of pulsatile flow in elastic tubes, the circulation of blood in animal arteries adds other problems. For example, the flow-ejection pattern of the heart is complex and the elastic properties of the arteries are non-linear. To analyze such a system it is necessary to simplify. This simplification can either take the form of an analogue model to represent the behavior of the whole circulation or to analyze individual sections of the circulation and attempt to build up a synthesis of the whole from component parts. Of the analogues that had been used previously the “Windkessel” completely dominated the field. The alternative approach of building from the investigation of single regions began, in McDonald’s case, experimentally with the measurement of pulsatile flow in arteries at the beginning of 1950, but only developed physical and mathematical direction with the collaboration of J.R. Womersley in 1953. The first step was the measurement of pulsatile blood flow in the basilar artery. From his observations here he was led to the consideration of pulsatile flow conditions in arteries in general, and within a few years McDonald, and the collaborators he attracted, had virtually transformed the subject. The core of his approach was the use of Fourier methods to describe arterial events as steady-state oscillations. This approach has since been followed by researchers throughout the world with enormously fruitful results.
- Copyright
- © 2007 Association for Research into Arterial Structure and Physiology. Published by Elsevier B.V. All rights reserved.
- Open Access
- This is an open access article distributed under the CC BY-NC license.
Feb. 6, 1973
Dear Wilmer,
You seem to have fallen into a hole of silence. I suppose you feel so superior up at Hopkins that you look down on us Southerners now!
When I last called Bill Milnor he said you had all gone off to Mississippi for Christmas—hope you had a good time, but was sorry you did not stop off in Birmingham. We had a very nice week with Penny and her husband—and of course Alison and Robin.
Give my regards to your boss (Bill Milnor). Renée sends her love to Arlene (and I do too) and to you (though you don’t deserve it).
All the best,
Ever yours,
Donald A. McDonald
Excerpts from the last letter I would receive from my mentor Dr McDonald.
Donald Arthur McDonald died May 24, 1973 in Birmingham, Alabama at the young age of 55 years (Fig. 1) from cardiac failure. He left behind his devoted and charming wife Renée who continues to live in Birmingham and who acts as a link for his former colleagues and students. His sons Neil and Robin and daughters Penny and Alison are all married, and all except Neil live with their families in the States; Neil lives in the UK. None of the children followed their father into the field of academic medicine and research, although his daughter, Alison, was his secretary for many years. Dr. McDonald was a very, very kind man with a colorful and witty personality. His career epitomized on the positive side the value of interdisciplinary research and on the negative side the trials and frustrations encountered by one who dares to be different. He and his wife Renée were avid bird watchers and encouraged their children to enjoy the great outdoors.

Donald Arthur McDonald (June 3, 1917–May 24,1973).
At the time of his death he was Professor of Physiology and Biophysics at the University of Alabama in Birmingham. During his short research career he published 34 scientific articles, some of which are considered classics, and two very influential books.
McDonald was born to English parents in Katni, India June 3, 1917 and educated at Christ’s Hospital School, where he won an open scholarship in Natural Science in 1936 to attend Oriel College, Oxford. He graduated with a B.A. in physiology in 1939, and then, having won the Gotch memorial prize and the Theodore Williams scholarship completed his B.M. at the Radcliffe Infirmary and Oxford University in 1942 when Britain was immersed in war. After an attenuated residency in Oxford and Leicester, he joined the Royal Army Medical Corps and worked predominantly in neurosurgery from 1943 to 1947. Even in war he maintained his intellectual curiosity and scholarship. He compiled a treatise on brain injuries and their neurological sequelae, which was successfully submitted as a thesis for the Doctorate of Medicine at Oxford University. In 1948 he was appointed Senior Lecturer in Physiology at St. Bartholomew’s Hospital, London, and was promoted to Reader in 1953. During his time in London he also received a Doctor of Science degree from the University of London. It was at St. Bartholomew’s that he started the work for which he will be remembered. His early research interest was in the measurement and study of stream line blood flow in the basilar artery.1 During this period in his life he established a working relationship with the great neurophysiologist, Professor W.R. Hess in Zurich, Switzerland.2–4 However, blood flow became more interesting to him than neurophysiology, and he and John Potter developed high-speed cinematographic techniques for measuring pulsatile blood flow in the basilar artery5–8 and aorta of rabbits9,10 and the femoral artery of dogs.11 Previous laws governing the relationship between pressure and flow in a tube were based on steady flow or hemostatic conditions and explained through Poiseuille’s equation which related flow to the pressure gradient along the tube. In an artery it is immediately apparent that the pressure is far from constant but is pulsatile owing to the pumping action of the heart. The rise and fall of pressure which is distributed throughout the arterial tree represents to some extent a change in the absolute level of pressure in a tube and so will not, of itself, directly influence the flow. McDonald realized that it was not surprising that no simple relationship between the pulsatile pressure in an artery and its flow had been previously discovered. If pulsatile flow and pressure are recorded together as in Fig. 2 we see that the maximum rate of flow precedes the maximum pressure, which appears odd when one considers that blood must have inertia.11,12 The apparent anomaly is due to the fact that, as in the application of Poiseuille’s law, it is the pressure gradient along the artery that is related to the flow of liquid and not the absolute pressure level.
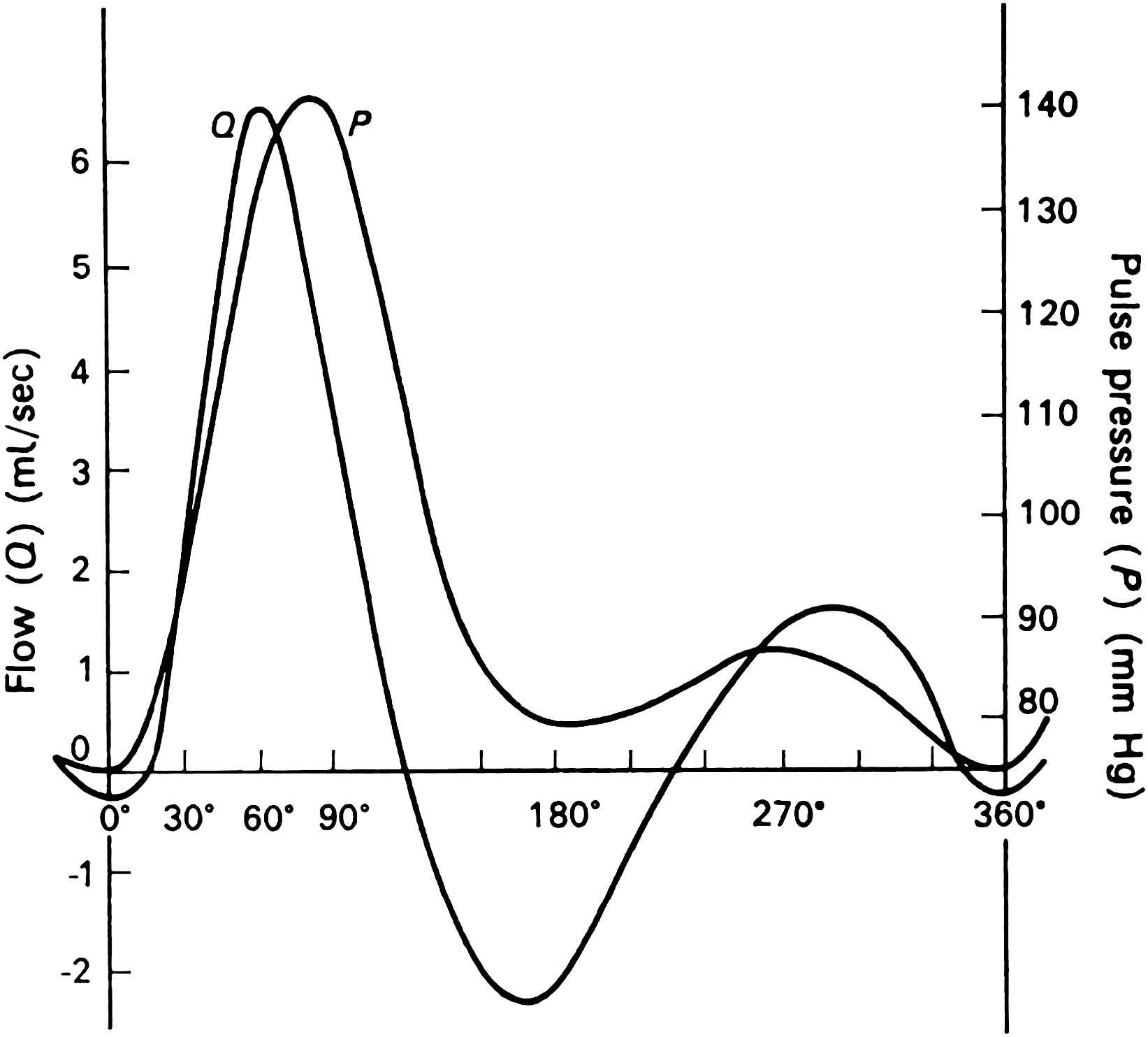
A flow velocity wave (Q) and the corresponding pressure pulse (P) recorded simultaneously in the femoral artery of a dog. The flow velocity was recorded by high-speed cinematography. Although superficially similar in shape when plotted on a comparable scale, the fact that the peak flow occurs before the pressure peak shows that there is no simple relation between these curves. The flow is, in fact, determined by the pressure-gradient.
The pressure-gradient may be easily determined by recording the pressure at two points along the artery and subtracting the pressure from the downstream point from that at the upstream point at each moment.12 The record of such a measurement is shown in Fig. 3. As the systolic pressure wave generated in the aorta by the expulsion of blood by the heart travels along the arteries the crest of the wave reaches the first recording point a short time before it reaches the downstream point. At this time the pressure is higher at the first than at the second point and the pressure-gradient slopes in this direction. The situation rapidly reverses and when the crest has reached the second point the pressure gradient is in the opposite direction. The oscillatory pressure gradient is surprisingly similar in shape to the flow wave, and Helps and McDonald used this notion to calculate pulsatile flow from the pressure gradient (Fig. 4).12

A diagram that shows how a traveling pressure wave creates an oscillatory pressure gradient. (A) Two pressure waves recorded a short distance apart in the femoral artery of a dog. The downstream wave is identical to the upstream one. (B) The pressure gradient derived by subtracting the pressure at the downstream site from that at the upstream one at 15° intervals and dividing by the distance between recording sites. (It should be noted that this gives a gradient opposite in sign to the usual mathematical convention for slopes.) (C) The derivative with respect to time (dP/dt) of the upstream pressure wave. The form of this curve and that of the pressure gradient (which in the limiting case of a very small interval is the derivative with respect of distance, dP/dz) is very similar. In this case, the only difference is due to the transmission time over the interval which is necessary to determine the gradient.

The flow velocity wave in the dog femoral artery recorded by high-speed cinematography compared with that calculated from a derived “pressure-gradient” (lower curve). The pressure-gradient was calculated from time-derivative of the pressure wave (dP/dt) and the pulse wave velocity.
In consideration of the pressure–flow relationships of pulsatile flow in arteries the vessel was treated as a simple tube of unvarying diameter. This neglects the fact that an artery is an elastic tube and a pulsating flow will cause it to vary in size. Another property of an elastic tube is that it will propagate a wave (pressure, flow and diameter) created by the ejection of blood from the heart, at a certain velocity which is largely determined by the elastic properties of the wall.11 In considering the relation of the pressure gradient to the form of the flow wave it was shown that this involved the velocity of travel of the wave. The model of the artery was, therefore, inconsistent. It was treated partly as a rigid tube, in that the movement of its walls was neglected, and partly as an elastic tube, in that the velocity of the pulse-wave was given its real value in the body. For it is well known that the wave velocity in a tube is largely determined by the elastic properties of its wall. In a rigid tube the wave would travel at the velocity of sound in the liquid.
For a full interpretation of the elastic behavior of the arterial wall it is necessary to know what proportion consists of elastic material and how that material is arranged. The elastic materials to be considered in an artery are collagen, elastin and smooth muscle. Previous estimates of their distribution had been made by histological techniques using differential staining. These, however, had little more than qualitative value. Chemical methods, however, became available that enabled collagen and elastin to be estimated more accurately. Harkness, Harkness and McDonald13 used these methods to estimate the proportions of collagen and elastin in various parts of the arterial tree of the dog. Their results showed that about 50 per cent of the vessel wall is made up of collagen and elastin, the remainder presumably being non-fibrous connective matrix and a relatively small amount of smooth muscle cells. They found that the distribution of elastin and collagen differed strikingly between the central and peripheral arteries. In the proximal aorta, elastin was the dominant component, while in the distal abdominal aorta the content reversed, and in peripheral arteries collagen dominated. In the thoracic aorta, elastin formed 60 per cent of the total fibrous element and collagen 40 per cent. In the extrathoracic arteries, the composition reversed, with elastin forming 30 per cent and collagen 70 per cent. The transition occurred rapidly over the distal 5.0 cm of the thoracic aorta above the diaphragm and over a similar distance in the branches leaving the arch of the aorta. This remained the same down to the smallest arteries they were able to study, such as the saphenous and internal mammary arteries.
Composition of the arterial wall and physical length and configuration of the arterial system determine arterial wall properties and wave reflection characteristics. These distinctive qualities of the arterial tree determine the morphology of the pressure and flow waves. Thus, although wave reflection is undoubtedly incomplete it can be seen that any point in the arterial tree is always close to a region that will cause reflections. The most remarkable feature of the change in morphology of the traveling pressure wave is the “peaking” of the wave; that is, the increase in overall amplitude as it travels toward the periphery.11 This is directly contrary to the expected behavior of waves propagated in a viscous medium where damping will cause a reduction in amplitude. There are two pieces of evidence which especially emphasize that this must be due to reflections. In the first place while the pressure pulse is increasing in size the amplitude of the flow pulse is decreasing markedly (Fig. 5). McDonald states that as the amplitude of both of these curves is mainly determined by the size of the first and second harmonic terms, which are of relatively long wavelength, we can simplify the discussion by considering their behavior alone; that is, we will ignore for the moment the formation of nodes and anti-nodes. The progressive change of amplitude in contrary sense of the pressure and the flow indicates that the peripheral parts of the arterial tree have a much higher impedance than the more central parts. An increase in impedance causes wave reflection in a “positive” sense, i.e. as from a partially closed end. In any system without end-effects of this kind the amplitude of the pressure oscillation and of the flow oscillation would be damped by the same amount as they traveled. The second analysis that makes it evident that there is a reflection of the pressure waves is that when there is “peaking” not only is the amplitude of the wave increased but also its variance. The variance is a measure of the energy content of the wave and can only show the apparently paradoxical effect of increasing as it travels if it is summating with a reflected wave. Also, in animals with short and/or stiff arteries, the central aortic pressure wave increases in late systole even though flow is decreasing. This can only occur if the incident or forward pressure wave summates with a reflected wave from down stream.
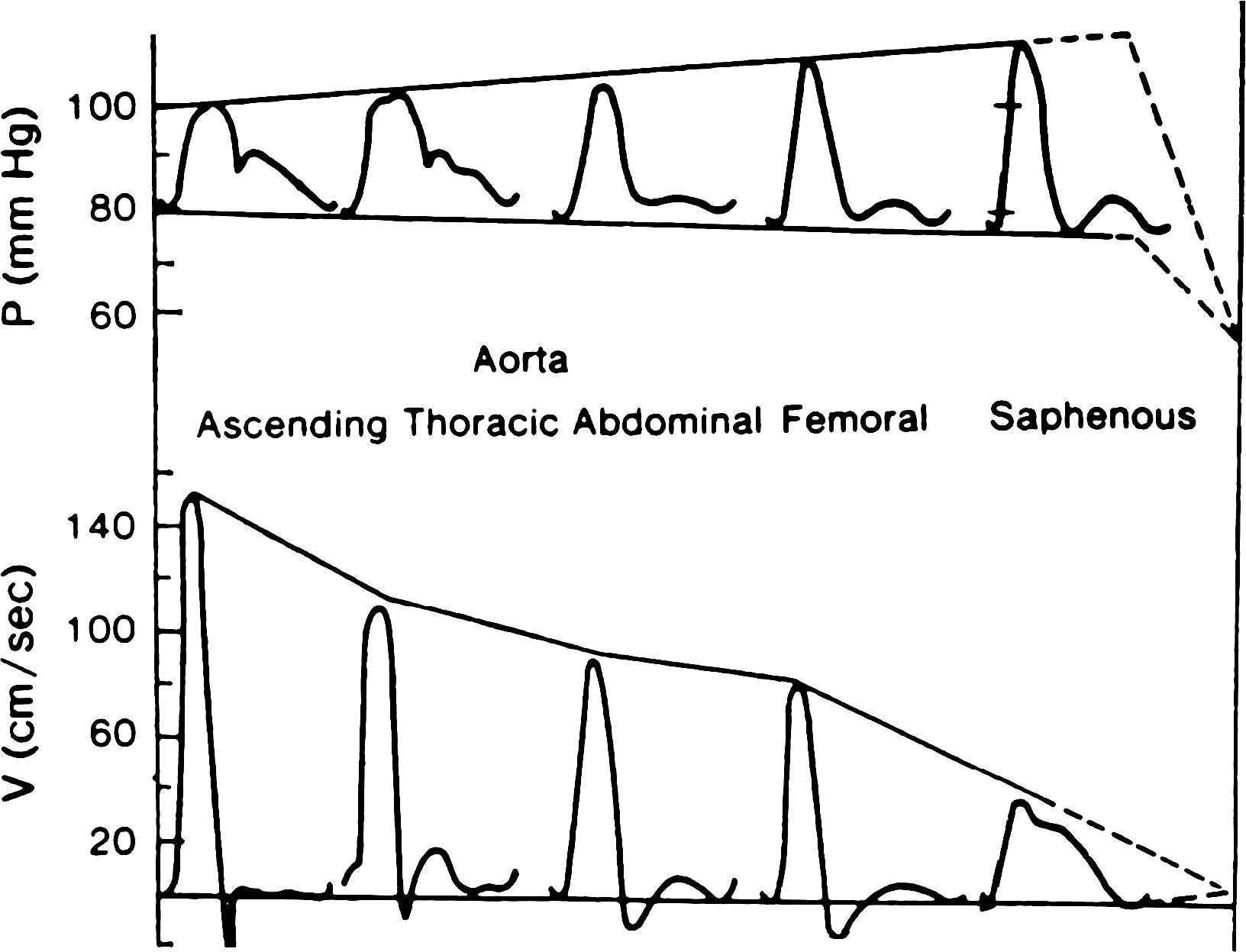
A diagrammatic comparison of the behavior of the pressure and flow pulses in arteries as they travel away from the heart toward the periphery. Mean pressure falls slightly but the pulsatile pressure variation increases until in the saphenous artery it may be double that at the root of the aorta. The flow oscillation, on the contrary, diminishes markedly. Such behavior can only be accounted for by the presence of a “closed” type of reflection in the small peripheral vessels. In the absence of reflections damping would cause a parallel fall in pressure and flow oscillations. Ultimately the pressure oscillations must also be damped out – the probable region of this fall is in the smallest arteries and proximal arterioles as indicated by the broken lines. The increase in ratio of the pulsatile pressure amplitude to that of the flow amplitude is largely determined by the increase in the fluid impedance of the low-frequency components; the change in shape of the pressure wave to that of the flow wave depends on the changes in impedance of the various frequency components in terms of their distance from the main reflecting sites, as the impedance is at a minimum at a quarter wave-length distance.
Pressure and flow recordings, however measured, created problems of interpretation and McDonald sought appropriate analytic methods that could give more information and he looked to the physical sciences for guidance. He was fortunate to strike up a relationship with John Womersley, then a most accomplished applied mathematician who also was seeking a new challenge.14–20 He stressed how interdisciplinary research can only advance on the basis of mutual respect, with all parties taking the time and effort to become familiar with their colleagues, and with none regarding any other as an instrument to success. McDonald was pressed to formulate his problems in a way that was subject to rigorous mathematical analysis. Womersley in turn was surprised at the imprecision of biological measurement and learned that a different approach was required of him than had been before because unlike physical science, biology is not an exact science. McDonald and Womersley worked most productively with each other over a 3-year period. During this time, Womersley tackled the Navier–Stokes equations as they apply to the motion of liquid in cylindrical tubes and showed that non-linearities in the arterial circulation are sufficiently small to be neglected to a first approximation. This was the basis for Womersley’s method for calculating pulsatile flow from the pulsatile pressure gradient, and for validation of longitudinal impedance by McDonald and Womersley.11,17 This work established the logic of using Fourier analysis to break down pressure and flow waves into modulus and phase and for the general concept of vascular impedance which was developed further by McDonald and Taylor in the late 1950s.21 In addition to system linearity and function periodicity, the pressure and flow waves must be measured accurately in order to use Fourier analysis. This can be done with measuring systems that have a flat frequency response to at least 10 Hz since the large majority of the wave energy (or total variance of the curve) is concentrated below this frequency. Generally speaking, the input impedance of a system is the opposition to pulsatile flow into the system. Ascending aortic input impedance is the opposition to pulsatile flow into the systemic arterial system and is, therefore, considered the best estimate of left ventricular afterload. Fig. 6 shows impedance moduli spectra calculated by McDonald at different sites in the arterial tree of a dog. These spectra were calculated from pressure waves previously published by Laszt and Muller22,23 and measured apparent phase-velocities. The impedance moduli at low frequencies increase and the minimum shifts to a higher frequency as pressure and flow measuring sites move further down the arterial tree. In the graph of the impedance in the proximal aorta it can be seen that there is a well-defined minimum at a frequency of about 4 c/s. This indicates a reflecting site at a distance of approximately 27 cm which, taken from the distal point of recording, is in the region of the bifurcation of the aorta, a region which causes marked reflection phenomena in the aorta. In the femoral artery the minimum occurs at a frequency of 6 c/s. indicating a major reflection site in the vicinity of the foot. By comparison the impedance pattern in the saphenous artery is seen to be falling sharply over all the frequencies measured and a minimum is far to the right. The difference between this graph and that for the femoral artery is due to proximity of the reflecting site. The reflection site itself, however, has not changed but the impedance is measured closer to it in the saphenous artery. The values of the characteristic impedance for each curve are also shown in Fig. 6. It can be seen that the characteristic impedance is 0.56 dyne sec-cm−3 × 103 in the proximal aorta, 1.67 in the femoral artery and 3.75 in the saphenous artery. The increase in impedance is to be expected as we move into smaller arteries because of increased stiffness. The changes produced in the impedance spectra with vasoconstrictor drugs in central arteries are similar to those measured in stiffer peripheral arteries. That is, the moduli at low frequencies and characteristic impedance increase and the minimum shifts to a higher frequency indicating increased wave reflection; vasodilation has an opposite effect.
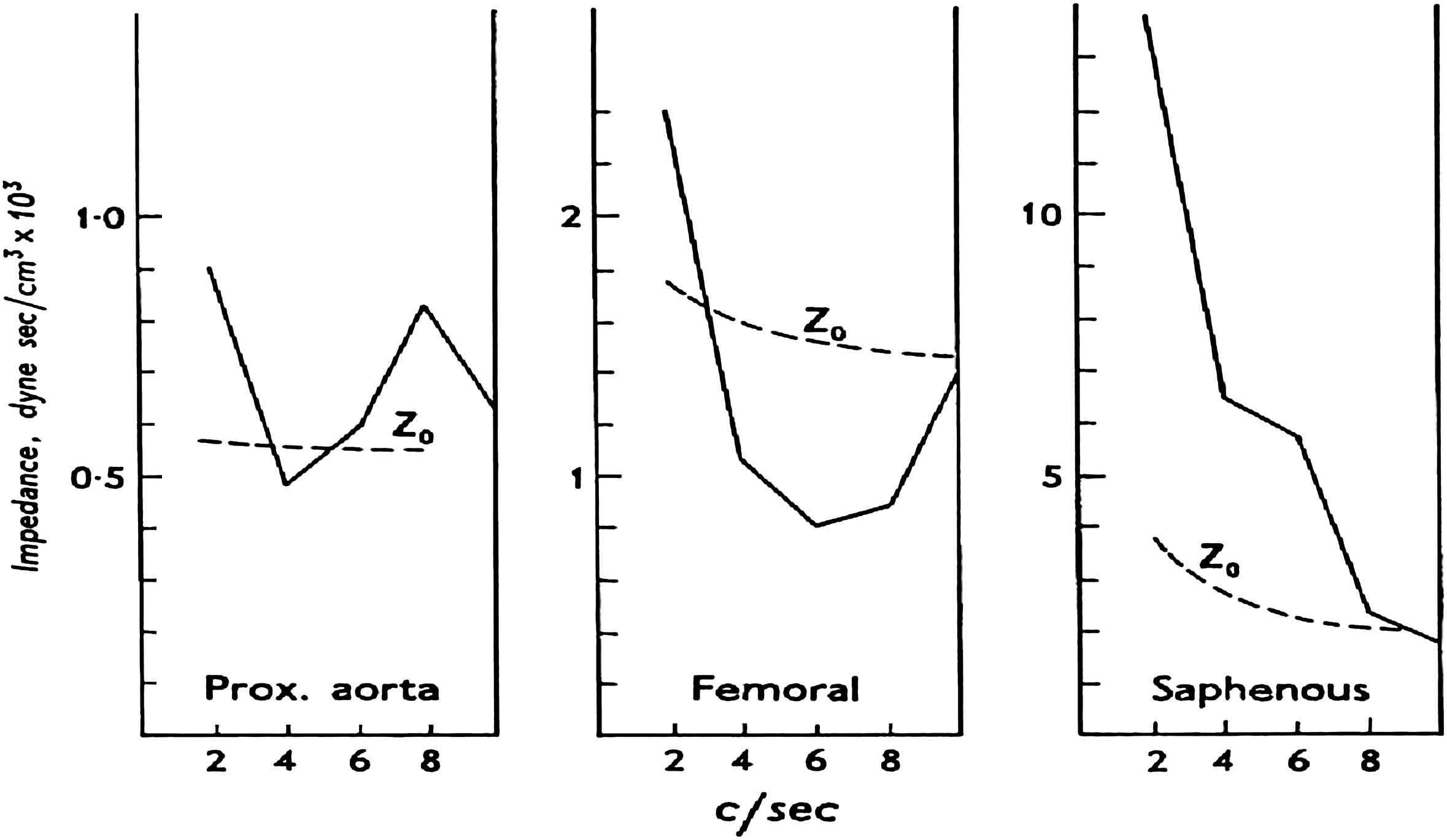
Values for the moduli of the input impedance at various sites in the arterial tree. These spectra are derived from data published by Laszt and Muller.23 The broken lines show the characteristic impedance (Zo) in each situation. (Note that the vertical scale is different in each graph.)
After Womersley’s departure for the Wright Air Development Centre in Columbus, Ohio, McDonald continued his studies on arterial hemodynamics at St. Bartholomew’s Hospital. This period was crowned with publication of his classic book Blood Flow in Arteries in 1960 by Edward Arnold. This summarized work of the previous ten years and presented in a way that was easily digested. To illustrate his style of writing, an abbreviated version of the acknowledgements of the first edition is given below24:
“The goddess of Chance is rarely thanked on occasions such as this. I am sure that this is not so much due to the ingratitude of scientists as to the fact that she plays some part in starting almost any research. In my case her interventions have been so helpful and so perfectly timed that I feel I must pay her homage. For, although this book appears under my name alone, it could never have been written-for there would have been little of any value to write about-without the immense help I have had from my principal collaborators, John Womersley and Michael Taylor.
My interest in the present subject arose from the chance observation of streamline flow in the basilar artery of the rabbit. This was in the course of a severely “practical” research, with Dr. (now Mr.) J. M. Potter, into some problems arising from cerebral radioangiography. This led to the use of high-speed cinematography as the only method we could think of to measure the flow velocity in the basilar artery. I then thought it would be interesting to exploit the technique in a study of pulsatile flow in other systemic arteries-sliding, as it were, into circulatory physiology down the vertebral arteries.
In 1949, and again in 1951, I had the honour to work with Prof. W.R. Hess in Zurich (on neurophysiological problems) and although his own great contributions to circulatory physics were made many years ago he gave me most stimulating help in this field, for which, and for his continuing encouragement, I am most grateful.
The collection of records of pulsatile flow velocity in arteries was interesting but proved unsatisfying because their interpretation was difficult in the absence of a quantitative method of analysis. Progress was only achieved when I had the great good fortune to arouse the interest and enthusiasm of that distinguished mathematician, the late J. R. Womersley, in these problems.
Womersley’s career has been so well described by Sir Charles Darwin in his Obituary notice (Nature, 3 May 1958) that I need say little of it, except that he had a wide experience in many fields of applied mathematics and so was thoroughly familiar with the experimental approach so necessary in this type of work. Quite apart from the most valuable analyses he did, and the stimulation of his personality as a friend, the three years over which we collaborated were a most valuable experience in the problems of working with someone trained in a different scientific discipline. Long periods of discussion during the first eighteen months of our collaboration (during which Womersley only had his leisure hours to devote to it) were necessary before I could formulate the physiological problems in a way that would make physical sense. Equally it was a long time before he knew enough about the physiology of the circulation to tackle it in a realistic way. Once the main objectives were clearly seen, advance was very rapid, especially as he was able to spend a whole year in this department (June 1954–55) supported by a personal grant from the Medical Research Council. I feel that unless colleagues from the physical sciences are prepared to spend a comparable amount of time in learning some physiology, then the value of such collaboration will always be limited. This field is littered with abstract analyses of the circulation by talented mathematicians which are of slight use because they have little contact with physiological reality. If only brief consultations are available, then my own experience indicates that we, as physiologists, must first get the problem into a mathematical form and use, as it were, our colleague as a translator, skilled in a language we cannot handle with any fluency. For no mathematical treatment is ever better than the primary assumptions on which it is based.
Womersley went to the U.S.A. in 1955 but good luck was still with me for, six months earlier, Dr. Michael Taylor had one day arrived on the doorstep (unannounced from Adelaide), asking if he could work at Bart’s for a year during the tenure of a C.J. Martin Research Fellowship. He was thus able to spend a few months in collaboration with John Womersley before the latter’s departure. While he remained in England my problems of collaborating with expert mathematicians were over. Taylor, with a training in medicine and physiological research has also a passion for mathematics such that he is technically the equal of many professionals in this field. If I do not here sufficiently express may admiration and gratitude for his contribution to this work it is only because, while we are exhorted to speak only good of the dead, it is deemed fulsome (or at least un-English) to speak too well of the living-especially one’s close friends. Let it suffice to say that the organization of the ideas on wave reflection and arterial input impedance are almost entirely due to discussions with him. In addition the whole text has been subjected to his critical scrutiny-but I should also apologize to him for not always acceding to his demands for more rigour (in the mathematical sense); any inaccuracies that physicists may find will almost certainly be due to my omissions, for the sake of simplicity, of this kind.
An important part in the clarification of my ideas (however relative that term may appear) was due to the innumerable discussions I had with my American friends during a visit to the States in the later part of 1956”.
After publication of Blood Flow in Arteries, McDonald continued his research in the study of pulsatile pressure-flow relations25 and improving techniques to test fluid-filled catheter-manometer systems.26 The studies outlined and discussed in his articles and text had taken him way ahead of his contemporaries. His work was well accepted by several investigators in the United States, notably, E.O. Attinger at the University of Pennsylvania, D.J. Patel and D.L. Fry at the National Institutes of Health, W.R. Milnor at Johns Hopkins University, M. Anliker at Stanford University, and R.S. Rushmer at University of Washington, but not at all in Great Britain.
He was passed over for the Chair of Physiology at St. Bartholomew’s Hospital when this position was vacated by K.J. Franklin. Frustrated and demoralized, he sought a position in the United States.
In 1962, Donald McDonald was appointed to a position as research associate in Philadelphia with E.O. Attinger and continued his studies on Fourier series analysis of biological systems.27 He had come under the very strong influence of Sam Talbot, who was the first Chair of the Bioengineering Department at Johns Hopkins University, and who had helped to create the Philadelphia position for McDonald with Attinger. At this time, the University of Alabama was recruiting for its rejuvenated medical campus in Birmingham. John Kirklin had been appointed Chief of Surgery, leaving the Mayo Clinic in Rochester, Minnesota at the peak of his career in cardiac surgery; Talbot himself accepted appointment as Chair of Bioengineering, securing at the same time a position for McDonald as Professor of Physiology and Biophysics. McDonald moved to Birmingham in 1966, but sadly, Talbot was stricken with cancer and died in Baltimore before he could move to Birmingham.
McDonald worked as Professor of Physiology and Biophysics at UAB until the time of his death in 1973. He directed work into the clinical sphere while continuing in basic physiology and hemodynamics. He influenced many young physicians and physiologists, including Nicholas Kouchoukos, Karl Weber, Joe Janicki and both of us. His own work in the United States for some reason never rose to the heights that it had reached in England. In Birmingham his research efforts were in the measurement of regional arterial pulse wave velocity using a delay line method,28,29 and the derivation of pulsatile flow from the time derivative of pressure30 and stroke volume from the aortic pressure wave.31,32 He did, however, publish an excellent invited review article on hemodynamics in the Annual Review of Physiology in 1968.33 In America, arterial hemodynamics was not a fashionable subject at that time, especially in the field of cardiology; however, the process set in motion by McDonald in the 1950s has exploded in recent years throughout the world with publications in all journals dealing with hemodynamics.
When McDonald died he was working on the drafts of the second edition of Blood Flow in Arteries. This eventually appeared in 1974 with the editorial assistance of his friends and colleagues, Wilmer Nichols and Bill Milnor.
Donald A. McDonald had a great influence on his profession. He established the value of Fourier analysis, arterial impedance, wave reflections and the validity of analyzing the arterial pulse in the frequency domain. He linked with engineers, mathematicians and physicians, and he encouraged his students and colleagues to do likewise. He was very vocal in presenting his views at national and international meetings and conferences, and was persistent in his criticism of work he considered poor or indifferent. Speakers at conventions feared his presence in the audience and all the more his move to the microphone at question and comment time. But his own work was based on approximations and on compromise. He was fair in his criticism and this enhanced the science he pursued. He was a warm and humorous human being and a highly intelligent and cultured man. He had a phenomenal memory, recalling and citing references verbatim. Few bettered him in queries on passages from the Bible, from the War Between the States, from literary classics, or from Italian opera. His influence continues to remain today.1 Third, fourth and fifth editions of his textbook were prepared by us and published in 1990, 1998 and 2005, respectively; the sixth edition is in preparation and will be published in 2010, the 50th anniversary of the first edition. The challenge in writing these editions has been to have it as factual, as lucid, as balanced, and as entertaining as McDonald’s first edition. Large segments of these editions were completely unchanged from the first edition because they could not be improved upon and probably never will.
References
Cite this article
TY - JOUR AU - Wilmer W. Nichols AU - Michael F. O’Rourke PY - 2007 DA - 2007/09/21 TI - The life and times of Donald A. McDonald JO - Artery Research SP - 1 EP - 8 VL - 2 IS - 1 SN - 1876-4401 UR - https://doi.org/10.1016/j.artres.2007.08.002 DO - 10.1016/j.artres.2007.08.002 ID - Nichols2007 ER -
