The Exponentiated Poisson-Exponential Distribution: A Distribution with Increasing, Decreasing and Bathtub Failure Rate
- DOI
- 10.2991/jsta.d.200512.002How to use a DOI?
- Keywords
- Complementary risks; Exponentiated distributions; Maximum likelihood estimation; Poisson-Exponential distribution; Reliability and survival analysis
- Abstract
In this paper we propose a new three-parameters lifetime distribution with increasing, decreasing and bathtub failure rate depending on its parameters. The properties of the proposed distribution are discussed, including explicit algebraic formulae for its reliability and failure rate functions, quantiles and moments. A simulation study is performed in order to verify the behavior of the maximum likelihood estimates. The methodology is illustrated on a real data set.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
The exponential distribution (ED) provides an elegant, simple and close form solution to many problems in lifetime testing and reliability studies. However, the ED does not provide a reasonable parametric fit for some practical applications where the underlying failure rates are nonconstant, presenting monotone shapes. In recent years, in order to overcome such problem, new classes of models were introduced based on variations of the ED. For instance, Gupta and Kundu [1] proposed a generalized ED, which can accommodate data with increasing and decreasing failure rate function. Kus [2] proposed another modification of the ED with decreasing failure rate function, while Barreto-Souza and Cribari-Neto [3] generalizes the distribution proposed by [2] by including a power parameter in his distribution.
Recently, Cancho et al. [4] introduced the Poisson-Exponential (PE) distribution whose cumulative distribution function is given by
As described by Marshall and Olkin [5], an exponentiated distribution can be easily constructed. It is based on the observation that by raising any baseline cumulative distribution function (cdf)
Hence, the cdf of the exponentiated PE (EPE) distribution is defined from (1) as
The paper is organized as follows: In Section 2 we present the probability density function, survival function and hazard function of the new distribution, the EPE distribution, and present graphics of such functions for some parameters values. Some properties of the EPE distribution are also presented in Section 2. In Section 3 we present the inferential procedure for the model parameters. Section 4 contains the results of a Monte Carlo simulation on the finite sample behavior of maximum likelihood estimates. In Section 5 the methodology is illustrated on a real data set. Some final comments in Section 6 conclude the paper.
2. THE EPE DISTRIBUTION
The probability density function (pdf) of the EPE distribution corresponding to the cdf (2) is given by
If
If
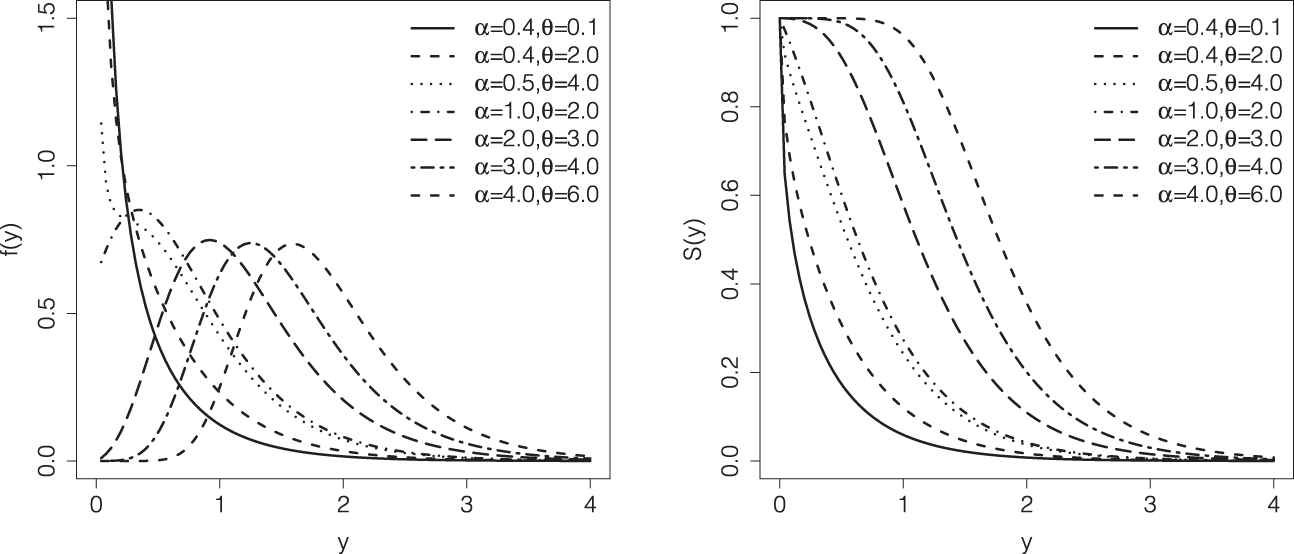
Left panel: probability density function of the exponentiated Poisson-Exponential (EPE) distribution. Right panel: survival function of the EPE distribution. We fixed λ = 2.
The EPE survival function is given by
Figure 1 (right panel) shows some survival function shapes for same fixed values of
The quantile
In particular, the median is
2.1. Failure Rate
From (3) and (6) it is easy to verify that the failure rate function is given by
The EPE distribution accommodates increasing, decreasing and bathtub failure rates depending on the parameter values. Define the function
Considering the inequality
If
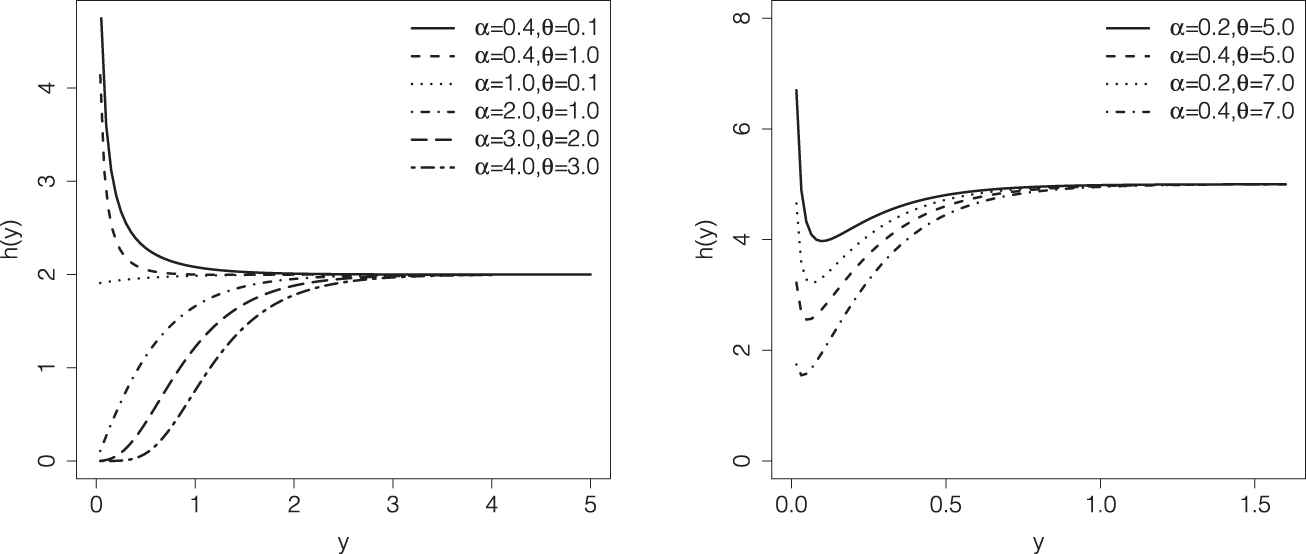
Failure rate function of the exponentiated Poisson-Exponential (EPE) distribution with λ = 2 (left panel) and λ = 5 (right panel) fixed.
2.2. Some Properties
Many of the most important features and characteristics of a distribution can be studied through its moments, such as mean, variance, tending, dispersion, skewness and kurtosis.
We shall now provide a general expression for the
We then formulate the following result.
Proposition 2.1.
Let
Proof.
The proof is obtained by direct integration and it is then omitted.
Order statistics are among the most important tools in nonparametric statistics and inference. Let
According to Barakat and Abdelkader [10], the
Consider the binomial series expansion given by
We then state the following.
Proposition 2.2.
For the random variable
Proof.
From (6) and (8), and using (9), (10) and the Taylor series of the exponential function
This completes the proof.
Given that a component survives up to time
Proposition 2.3.
For the random variable
Proof.
From (11), using (6), (9), (10) and the Taylor series of the exponential function
Then, we obtain the mean residual life of the EPE distribution as
On the other hand, we analogously consider the reversed residual life and some of its properties. The reversed residual life can be defined as the conditional random variable
The
Proposition 2.4.
For the random variable
Proof.
From (12) and using
Now using (9) and proceeding a similar way in the proofs of Propositions 2.2 and 2.3 follow the result.
Thus, the mean of the reversed residual life of the EPE distribution is given by
The Bonferroni and Lorenz curves (see [14]) and Gini index have many applications not only in economics to study income and poverty, but also in other fields like reliability, insurance and medicine. The Bonferroni curve
Proposition 2.5.
From the relationship between the Bonferroni curve and the mean residual lifetime given by Theorem 2.1 of Pundir et al. [15], the Bonferroni curve of the distribution function
Proof.
From (13) and using
Now using (9) and making binomial expansion a similar way in the proofs of Propositions 2.2–2.4 follow the result.
Also, the Lorenz curve of
The scaled total time and cumulative total time on test transform of a distribution function
Finally, the Gini index can be obtained from the relationship
3. INFERENCE
In this section we discuss inference and interval estimation for the model parameters.
3.1. Estimation by Maximum Likelihood
Let
The maximum likelihood estimates (MLEs) of
The Eq. (17) can be solved exactly for
3.2. Interval Estimation
For EPE distribution the Fisher information matrix is given by
The above expressions depend on some expectations that can be easily computed using numerical integration.
Large sample inference for the model parameters can be based, in principle, on the MLEs and their estimated standard errors. Following Cox and Hinkley [16], under suitable regularity conditions, it can be shown that
For testing goodness of fit of the EPE distribution and for comparing this distribution with some of its special cases, we consider the likelihood ratio statistics (LRS). For instance, for comparing the EPE distribution with the PE distribution proposed by [4] for a given data set we consider the hypothesis test given by
4. SIMULATION STUDY
This section presents the results of a simulation study that has been performed in order to verify the behavior of the standard errors, bias and root mean squared errors of the maximum likelihood estimators of
| n | ||||||
|---|---|---|---|---|---|---|
| 30 | ||||||
| 50 | ||||||
| 100 | ||||||
| 200 | ||||||
| 500 | ||||||
The averages of the
5. APPLICATION
In this section we consider a real data set of
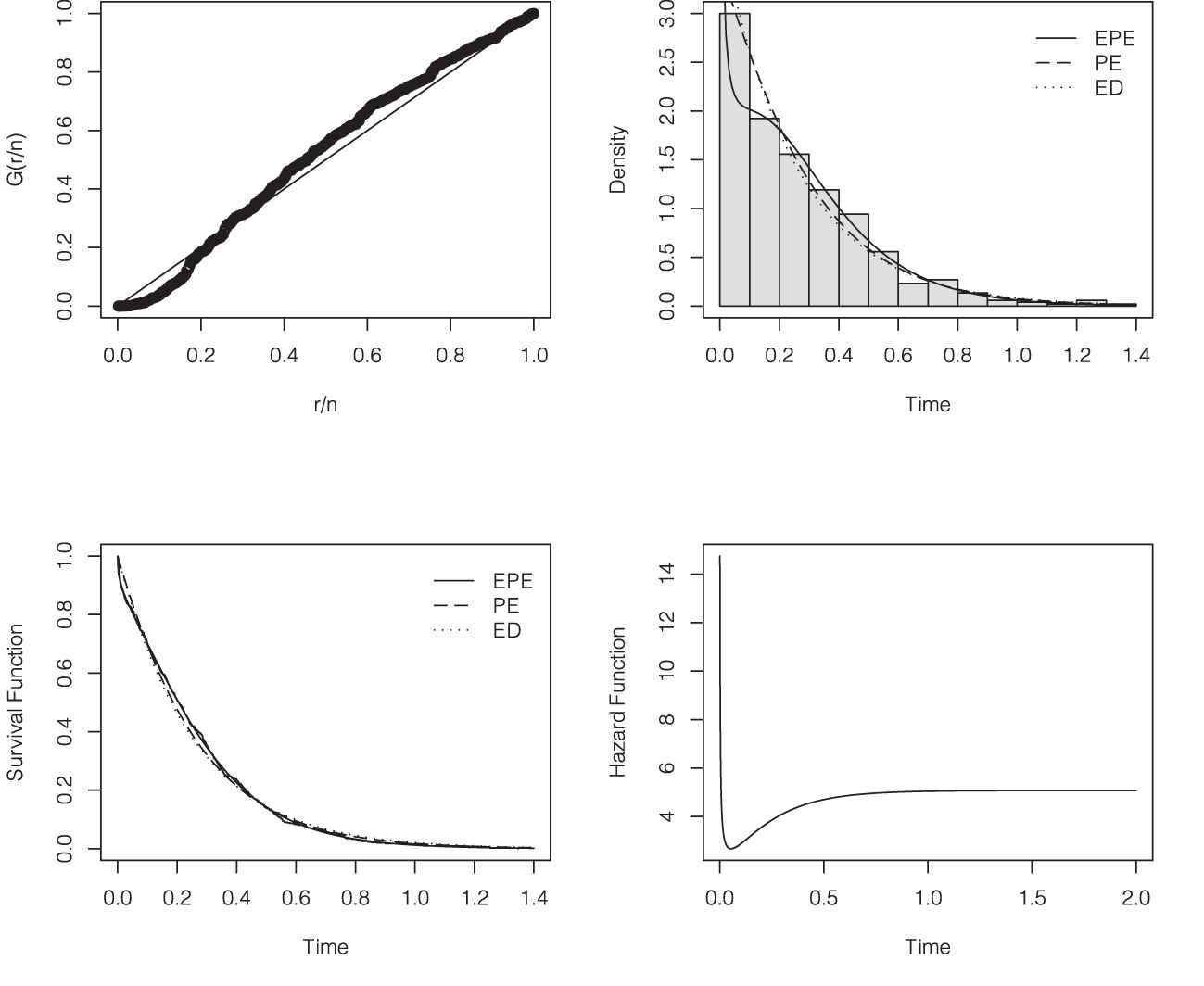
Upper-left panel: empirical scaled TTT-Transform on the real data set. Upper-right panel: histogram with estimated densities of the exponentiated Poisson-Exponential (EPE) distribution, PE distribution and exponential distribution (ED). Lower-left panel: Kaplan–Meier curve with estimated survival functions of the EPE distribution, PE distribution and ED. Lower-right panel: estimated hazard function of the EPE distribution.
Then, the EPE distribution was fitted to the data. Table 2 presents the MLEs and the corresponding
| Parameter |
||||
|---|---|---|---|---|
| Distribution | ||||
| EPE | ||||
| [ |
[ |
[ |
||
| PE | − | |||
| [ |
[ |
|||
| ED | − | − | ||
| [ |
||||
MLE, maximum likelihood estimate; EPE, exponentiated Poisson-Exponential; ED, exponential distribution; PE, Poisson-Exponential.
MLEs and their corresponding 95% confidence intervals.
As discussed in Section 3.2, for comparison of nested models, which is the case when comparing the EPE distribution with the PE distribution and the PE distribution with the ED, we can compute the maximum values of the unrestricted and restricted log-likelihoods to obtain the LRS. Thus, the LRS used for testing
Besides, for the sake of illustration, in order to compare our EPE distribution with other lifetime distributions capable of modeling a bathtub-shaped failure rate function, we fitted the exponentiated Nadarajah-Haghighi (ENH) distribution developed by Lemonte [18], with pdf given by
6. CONCLUDING REMARKS
In this paper we propose a new lifetime distribution. The EPE distribution is a generalization of the PE distribution proposed by [4], which accommodates increasing, decreasing and bathtub failure rate functions. It arises on a latent complementary competing risks scenario, where the lifetime associated with a particular risk is not observable but only the maximum lifetime value among all risks. We provide a mathematical treatment of this new distribution including explicit algebraic formulaes for its survival function and failure rate function, quantiles and moments. We discussed maximum likelihood estimation, which presented an adequate numerical stability in the simulation study performed. The EPE distribution allows a straightforwardly nested hypothesis testing procedure for comparison with its PE distribution particular case. The practical relevance and applicability of the EPE distribution were demonstrated in a real data set.
CONFLICT OF INTEREST
No conflict of interest has been reported by authors.
AUTHORS' CONTRIBUTIONS
(i) Vicente G. Cancho wrote the initial drafts of the paper and R codes; (ii) Paulo H. Ferreira helped in writing and improving the manuscript and the R programs, and also did the simulation study and analysis; and (iii) Francisco Louzada helped in the paper writing and supervised overall work.
ACKNOWLEDGMENTS
The research of Francisco Louzada is funded by the Brazilian organization CNPq.
REFERENCES
Cite this article
TY - JOUR AU - Francisco Louzada AU - Vicente G. Cancho AU - Paulo H. Ferreira PY - 2020 DA - 2020/06/15 TI - The Exponentiated Poisson-Exponential Distribution: A Distribution with Increasing, Decreasing and Bathtub Failure Rate JO - Journal of Statistical Theory and Applications SP - 274 EP - 285 VL - 19 IS - 2 SN - 2214-1766 UR - https://doi.org/10.2991/jsta.d.200512.002 DO - 10.2991/jsta.d.200512.002 ID - Louzada2020 ER -
