1. Introduction

Silicon neuron is electronic circuit that mimics electrophysiological behavior of neurons. It is supposed to be used as the basic elements of silicon neural networks, whose aim is to simulate the behavior of the nervous system in real-time or faster. They can be used not only as the high-speed brain simulators for neuroscientific researches but also as a basic technology for the next generation low-power intelligent computing systems. In addition, they can be used to construct bio-silico hybrid systems in connection with neurons, which can be an ideal technology for neuroprosthetic devices.

In this research, we focus on an analog silicon neuron circuit designed by using the techniques of qualitative neuronal modeling whose power consumption is as low as about 3 nW.¹ This circuit is composed of metal-oxide-semiconductor field-effect transistors (MOSFETs) in their subthreshold region for low-power consumption. By utilizing the qualitative modeling techniques, the model of this circuit was designed so that it can reproduce the dynamical structures in the excitable nerve membrane. The parameter tuning procedure is supported by the feedback amplifiers integrated in the silicon neuron circuit.

The characteristics of this circuit are influenced by temperature, transistors’ fabrication mismatch, and their secondary effects (short channel effect, etc). They make the expected circuit characteristics in designing stage and actual behavior of the individual circuit inconsistent. Therefore, it is required to adjust bias voltages of transistors in silicon neuron circuit to get the desired dynamical behavior.

The procedure to do it by hand has been established³, but it is not realistic to execute the procedure for each silicon neuron circuit when we build the large-scale silicon neuronal networks comparable to the human brain which contains about 100 billion neurons.

To solve this issue, a system to fit characteristics of silicon neuron automatically is essential. In this work, the same metaheuristic algorithm used in the previous similar works^{2, 3, 4}, the Differential Evolution (DE) method⁵, is used to find proper bias voltages. The DE method performed better in terms of convergence speed and simulation time, compared to other popular metaheuristic algorithms, such as Genetic Algorithm and Simulated Annealing.³ All the results in this work was obtained by circuit simulation using ngspice.

Our silicon neuron model is explained in the next section and our parameter fitting algorithm is in section 3. The results and discussion are in section 4 and 5, respectively.

2. A low-power analog silicon neuron model

Our silicon neuron circuit is composed of two blocks, the v- and n-blocks (Figure 1). Each block’s dynamics is represented as below.

Fig. 1.

Block diagram of our qualitative-modeling-based low power silicon neuron circuit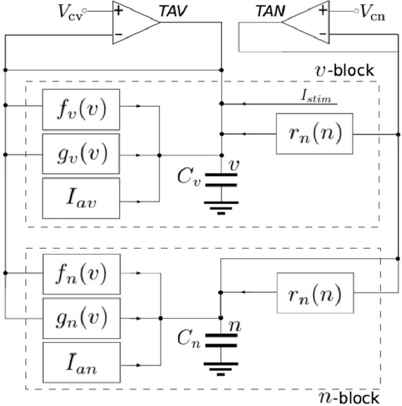

For each function, f_x(v) (x = v, n) is an ideal I-V characteristics of a differential pair circuit, g_x(v) and r_n(n) are ideal I-V characteristics of a cascoded transistor circuit with source degeneration with a detached bulk voltage. Both of them are in sigmoidal shape and the latter has shallower gradient than the former. They are combined to construct the mathematical structures in the neurons. I_ax and I_stim are constant current and input stimulus, respectively. They are generated by transconductance amplifiers.

There are nine bias voltages to tune this circuit, one of which is related to the time constant of n and the others affect the shape of the sigmoidal curves.

Our circuit can reproduce Class1 and 2 neurons in the Hodgkin’s classification⁶, by reconstructing specific dynamical structures for each class. In this work, we concentrated on the Class1 neuron mode of our circuit.

To estimate the dynamical structures in our circuit, the transconducance amplifiers (TAV and TAN in Figure 1) are used to draw the nullcline of each variable. The nullclines are drawn by measuring the current I_v, the output current of TAV, and I_n, the output current of r_n(n), while sweeping V_CV in DC analysis. Their equations are represented as below.

3. Automatic parameter voltages fitting algorithm

Figure 2 illustrates the block diagram of our automatic parameter fitting system. Here, we use circuit simulation instead of actual circuit measurement because this work focuses on the efficient verification of our fitting algorithm in this system. It finds the appropriate parameter values by optimizing the difference between the reference data and the simulation result.

Fig. 2.

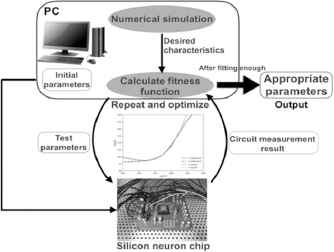
Automatic bias voltages tuning system for silicon neuron

This optimization is done by using the DE method which searches for the best-fitted parameter vector by repeating the mutation, crossover, and selection of parameter vectors for a number of generations. The automatic parameter fitting algorithm we suggest is composed of the 2 steps explained below.

3.1. Step1: Fitting nullclines

At first, we fit the shape of the v- and n-nullclines to a given reference nullclines. Figure 3 shows the nullclines in the Class1 neuron mode without stimulus. The two nullclines intersect each other at three points, “S”, “T”, and “U”. They represent a stable node, a saddle point, and an unstable node, respectively. Point “S” corresponds to the resting state and “T” is responsible for the threshold phenomena of neuronal spike generation.

Fig. 3.

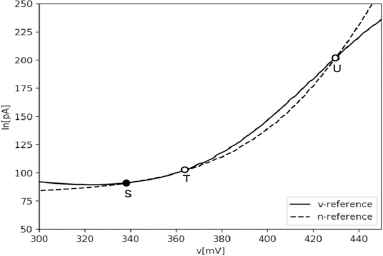
Nullclines in the Class1 neuron mode

The fitness function for the DE method is calculated by summing the difference between the nullcines obtained in the simulation and the reference nullclines. The fitness function is written as follows:

(5)F1=1N∑i=1N(si(x)−ri,x)2,i=1,2⋯N,N=75,  x=v,n,

where s_i(x) and r_i,x represent the coordinate of a point on the nullclines in simulation result and the reference nullclines, respectively. i is index of each point and x represents v or n. The voltage range of the nullclines is limited to between 300 and 450 mV. This range covers the three intersections of the nullclines in the Class1 neuron mode. Four parameters, fx_Vb, fx_Vdlt, gx_Vm, Iax_Vin (x=v, n) are tuned for each nullcline. Parameter rn_Vm is fixed at a random value in this step.

Initial vectors are generated in the range between − 100mV and +100mV compared to the values used for generating the reference data. The DE method’s optimization step was repeated for 400 generations and 40 vectors were contained in each generation.

4. Results

Table1 shows the characteristic of our silicon neuron circuit with the parameters obtained by our fitting algorithm. For all the criteria, the error is less than 4%.

Figure 4 shows the reference transient data and simulation results of the fitted circuit. The amplitude of spikes seems to be well fitted.

Fig. 4.

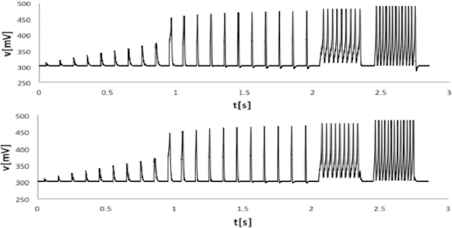
Transient data of the reference (top) and the simulation results of the tuned circuit (bottom)

The reference data was generated by using ngspice simulation. Thus the ideal fitting result is identical to the parameter set used for the reference data generation, with which the error is zero. But as shown in Table 1, our algorithm could not find the original parameter set but found a local optimum point.

Table 1.

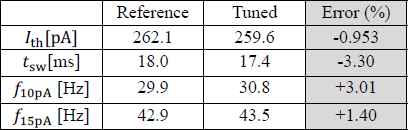
Comparison of silicon neuron characteristics

5. Discussion

In this research, we proposed an algorithm to find proper parameter values to obtain the desired dynamical properties for individual silicon neuron circuit instance. This algorithm will be crucial for operation of large-scale silicon neuron networks. The error for the criteria in the fitting procedure was less than 4%. From the viewpoint of engineering application, defining the maximum acceptable error is a difficult problem, because it depends on specific applications but they are not established yet. From the viewpoint of neuromimetics, this error is acceptable when our algorithm is used to tune a number of silicon neuron instances to Class 1, because there is a wide distribution (far larger than 4%) of dynamical properties in the same class of neuronal cells.

We will also try to apply this algorithm in fitting Class2 neuron. In addition, our algorithm will be improved to be applicable to the three variable ultralow-power silicon neuron circuit.⁷ This circuit can realize a wide variety of neuronal classes such as the regular spiking, the square-wave bursting, and the elliptic bursting.

In the future, we will apply this algorithm to a real circuit.

Acknowledgement

This study was partially supported by JST PRESTO and CREST and JSPS-MAEDI SAKURA Program.