Unified Approach to (1 + 1) Evolutionary Algorithm on Discrete Linear Functions
- DOI
- 10.2991/jrnal.k.190602.001How to use a DOI?
- Keywords
- Evolutionary algorithm; discrete linear function; (1 + 1) EA; PO-mutation; PO-EA
- Abstract
We consider the runtime property of discrete linear functions in (1 + 1) Evolutionary Algorithms (EAs), Partially Ordered mutation (PO-mutation) and Jansen’s model, Partially Ordered Evolutionary Algorithm (PO-EA). We analyze the process of evolution. This study was motivated by the paper of Jansen treating the runtime property of (1 + 1) EA on monotonic functions by means of probabilistic theory. As linear functions are special cases of monotonic function, we analyze their behavior. We show that the (1 + 1) EA can obtain an optimum solution at a stable hitting time for discrete linear functions. When the mutation rate is weak, on the order of 1/l, most monotonic functions behave similarly and can be approximated well by the PO-mutation model.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Discrete optimization is a generic term for mathematical programming that minimize or maximize a given function f(x) under the constraint that the solution x belongs to a set feasible region with discrete properties. It is depending on whether the condition that defines the set feasible area is a combinational condition or an integer condition, it may be roughly divided into combinatorial optimization and integer optimization. In this research area, there are researchers who try to capture the characteristics of the optimization function f(x) to make optimization easy to handle [1]. We are also interested in the properties of this optimization function. In the area of discrete optimization, there are many interesting properties that facilitate the optimization task [2]. One of them is monotony. Monotonic submodular functions have recently been applied in the field of machine learning. This paper focuses on optimization functions that are monotonic functions.
The Partial Order Evolutionary Algorithm (PO-EA) model introduced by Jansen [3] contributes to the analysis of performance in linear functions and is expected to simulate the optimization of monotonic functions [4,5]. PO-EA is a pessimistic model of the true optimization process, which can be used to derive an upper bound on the expected hitting time of monotonic functions. PO-EA was divided into two parts by Ma et al. [6]. These are called PO-mutation and ZeroMax models, respectively. In this study, we used a PO-mutation model. The PO-mutation model contains mutations that increase the fitness of every monotonic function.
In this study, we assumed that the optimum binary string is {1}l, and use typical monotonous discrete linear functions on (1 + 1) EA, PO-mutation and PO-EA. The optimum hitting time calculated by computer experiments could confirm the contribution of (1 + 1) EA, PO-mutation and PO-EA, and help to understand the mechanism of the optimization process of EA.
2. MATHEMATICAL MODELS OF EAs
An EA is a generic term for a search model or algorithm for searching for an optimal solution by imitating the process of inheritance or evolution of an organism. This method evolves a group of solutions and obtains an optimal solution by repeating generational change based on change and selection on a problem. We can apply to various problems as long as we can represent gene numbers and set fitness evaluation functions. However, even in the case where a single search can be performed in a short time, a problem in which the number of all solutions is enormous may take too much time for the calculation itself and may not reach an effective solution. EA can be classified into genetic algorithm, evolutionary strategy, and evolutionary programming.
In this study, we use the simplest (1 + 1) EA, in which both the number of parent and offspring genes are one [7]. Genes are represented by binary string. A gene of length i can be written as (x1, x2, ..., xi) (where xi = 0 or 1). In addition, gene mutation means that the value of each xi is inverted according to the probability pm. We called it mutation probability. If the function f(x) is defined in an interval [a, b] and f(x) ≤ f(x′) for any x, x′ (x < x′) in the interval, f(x) is said to be a monotonically increasing function in the interval [a, b]. If f(x) ≥ f(x′), then f(x) is said to be a monotonically decreasing function in the interval [a, b]. These are generically called monotonic function.
In the past research, Furutani et al. [8] analyzed the expected hitting times of EAs and Random Local Search by applying Markov chain. They showed that using pm = 1/l, the runtime of the Markov chain is approximately given by l log(l), where l is the length of the gene and l is large enough. In this study, we also set pm = 1/l.
3. EVOLUTIONARY ALGORITHMS
3.1. (1 + 1) Evolutionary Algorithm
(μ + λ) Evolutionary algorithm came from Evolutionary Strategy developed by Rechenberg and Schwefel, where μ and λ are numbers of parent and offspring solutions, respectively. We set μ = 1 and λ = 1. These are the simplest combinations, and represented by (1 + 1) EA. It is too simple for an analysis, it has following properties [2].
- (1)
It is efficient for many problems.
- (2)
It cannot get stuck in a local optimum.
- (3)
The analysis of it reveals many tools that can be used in more practical algorithms.
The algorithm of (1 + 1) EA is given by Algorithm 1. In this algorithm, x are binary strings and f(x) are optimization functions.
| 1: Initialize x ∈ {0, 1}l uniformly at random. |
| 2: Create x′ by flipping one each bit in x with probability pm. |
| 3: Select if f(x′) ≥ f(x) then x := x′. |
| 4: Go to 2 until a termination condition is fulfilled. |
(1 + 1) EA
3.2. PO-mutation Algorithm
Colin et al. [5] have shown that PO-EA can be divided into two parts. Ma et al. [6] have named it PO-mutation and ZeroMax models. They treated two selection conditions, (x′ ≥ x) and {(
| 1: Initialize x ∈ {0, 1}l uniformly at random. |
| 2: Create x′ by flipping one each bit in x with probability pm. |
| 3: Select if x′ ≥ x then x := x′. |
| 4: Go to 2 until a termination condition is fulfilled. |
PO-mutation
In the comparison x and x′, (x′ > x) means that every bit changes were only from 0 to 1, (x′ < x) means that every bit changes were only from 1 to 0, and (
We assumed that {1}l is the optimum string in the step 3 Selection process of Algorithm 2. PO-mutation model is used to investigate PO-EA convergence properties, so this model cannot be used to the problems whose the optimum string is not known.
3.3. Partial Order Evolutionary Algorithm
Jansen introduced the PO-EA model [3]. The algorithm of PO-EA is given by Algorithm 3.
| 1: Initialize x ∈ {0, 1}l uniformly at random. |
| 2: Create x′ by flipping one each bit in x with probability pm. |
| 3: Select if (x′ ≥ x) OR {(
|
| 4: Go to 2 until a termination condition is fulfilled. |
PO-EA
The difference of three algorithms are Selection in the step 3.
4. NUMERICAL EXPERIMENT
As an optimization function, we apply discrete linear function f(x)
Since many studies suggested that the mutation probability of pm = 1/l may be the best choice, we carried out our analysis using this value.
In this section, we compare the first hitting time of the numerical experiments of (1 + 1) EA, PO-mutation and PO-EA with s = 0.0, 1.0 and 0.5. We used the mutation rate pm = 1/l. The length of the string is l = 100, and we performed 10,000 runs for each parameter set, and averaged over them.
Figure 1 shows the time dependence of the probability of the first hitting time of optimum solution in (1 + 1) EA, PO-mutation and PO-EA with s = 0.0. These lines are the results of numerical calculation. The result is moving averaged with window size of 30. The red line is the result of PO-mutation calculation. The green line is the result of PO-EA calculation. In Figure 1, the waveforms of (1 + 1) EA and PO-mutation are similar, but PO-EA is behind the other. The mean of the first fitting times in (1 + 1) EA, PO-mutation and PO-EA are 1069, 1014 and 1976, respectively.
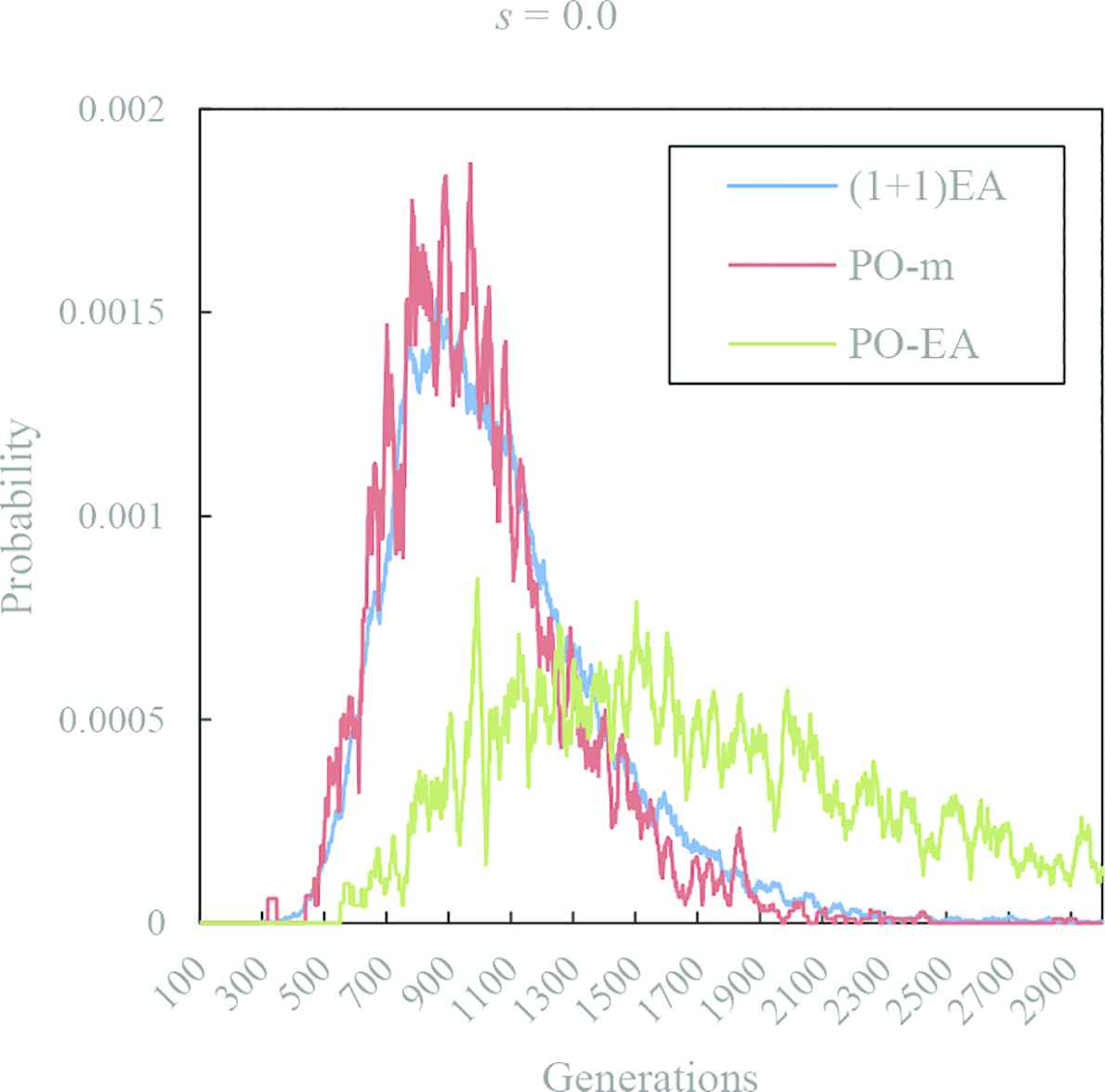
The distribution of the first hitting time of optimum solution in (1 + 1) EA, PO-mutation and PO-EA with s = 0.0. The blue line is the result of (1 + 1) EA calculation. The red line is the result of PO-mutation calculation. The green line is the result of PO-EA calculation.
Figure 2 shows the time dependence of the probability of the first hitting time of optimum solution in (1 + 1) EA, PO-mutation and PO-EA with s = 1.0. The red line is the result of PO-mutation calculation. The green line is the result of PO-EA calculation. In Figure 2, the peak of the first hitting time is delayed in order of PO-mutation, (1 + 1) EA and PO-EA. The mean of the first fitting times in (1 + 1) EA, PO-mutation and PO-EA are 1136, 1008 and 1295, respectively.
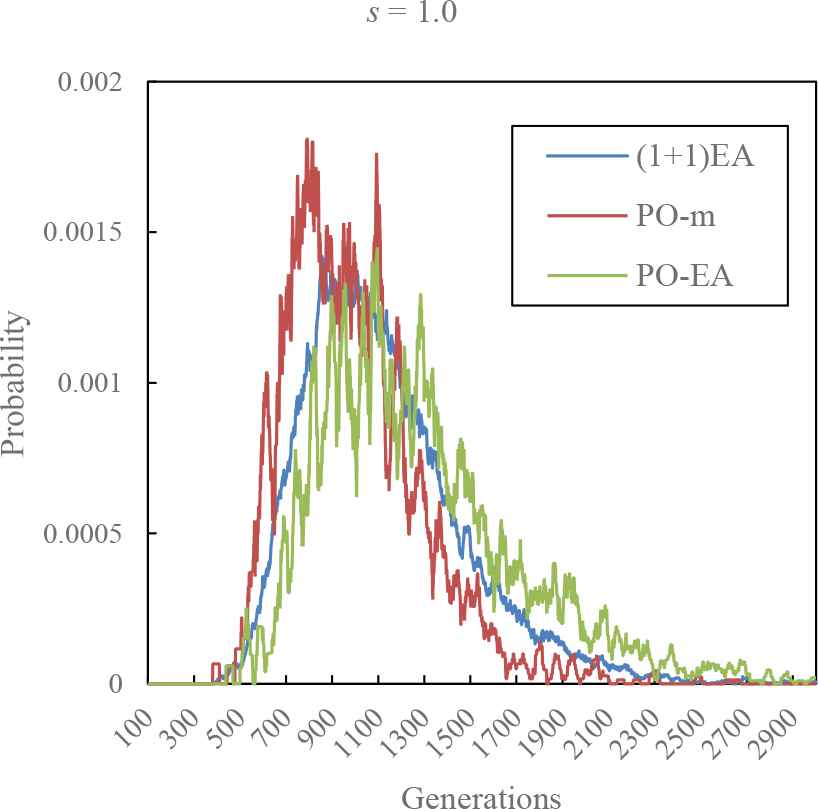
The distribution of the first hitting time of optimum solution in (1 + 1) EA, PO-mutation and PO-EA with s = 1.0. The blue line is the result of (1 + 1) EA calculation. The red line is the result of PO-mutation calculation. The green line is the result of PO-EA calculation.
Figure 3 shows the time dependence of the probability of the first hitting time of optimum solution in (1 + 1) EA, PO-mutation and PO-EA with s = 0.5. The red line is the result of PO-mutation calculation. The green line is the result of PO-EA calculation. In Figure 3, as in Figure 1, the waveforms of (1 + 1) EA and PO-mutation are similar. PO-EA is behind the other, but it is not as late as Figure 1. The mean of the first fitting times in (1 + 1) EA, PO-mutation and PO-EA are 1050, 1018 and 1280, respectively.
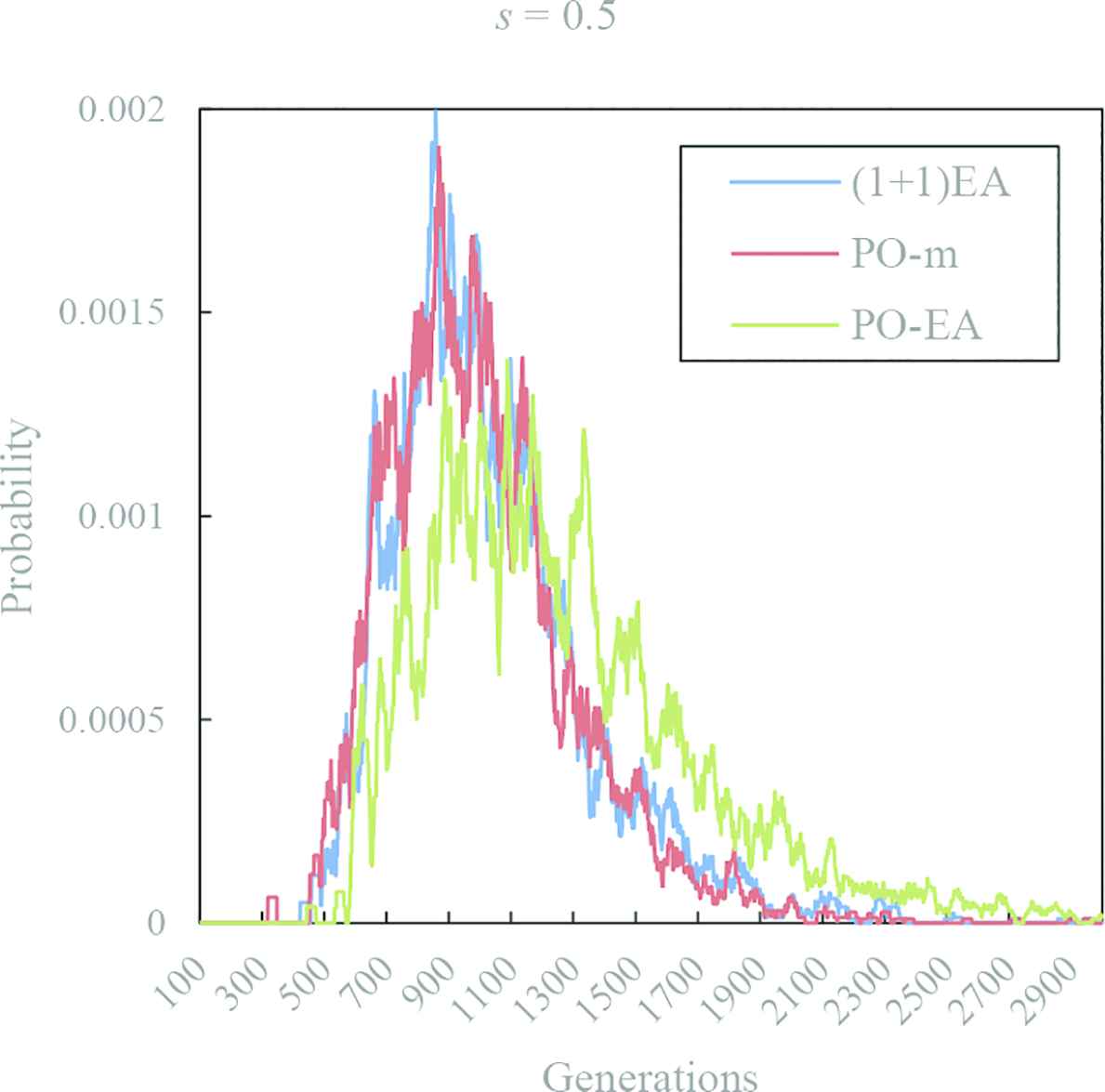
The distribution of the first hitting time of optimum solution in (1 + 1) EA, PO-mutation and PO-EA with s = 0.5. The blue line is the result of (1 + 1) EA calculation. The red line is the result of PO-mutation calculation. The green line is the result of PO-EA calculation.
5. SUMMARY
In this paper, we studied time behavior of (1 + 1) EA, PO-mutation and PO-EA to understand how evolutionary computation works for discrete linear functions. We demonstrate that the (1 + 1) EA can obtain an optimum solution at a stable hitting time for discrete linear functions. When the mutation rate is weak, on the order of 1/l, most monotonic functions behave similarly and can be approximated well by the PO-mutation model. These studies can help to understand the working mechanism of EA, and give some suggestions to design algorithms for other problems.
CONFLICTS OF INTEREST
There is no conflicts of interest.
Authors Introduction
Dr. Kenji Aoki
 He received his PhD of Engineering from Kagoshima University in 2010. He is currently working in Information Technology Center at University of Miyazaki as Associate Professor, since 2010. His research interests include bio-informatics, evolutionary computation, information system and Intelligent systems. He is a member of IPSJ and JSET.
He received his PhD of Engineering from Kagoshima University in 2010. He is currently working in Information Technology Center at University of Miyazaki as Associate Professor, since 2010. His research interests include bio-informatics, evolutionary computation, information system and Intelligent systems. He is a member of IPSJ and JSET.
Dr. Makoto Sakamoto
 He received his PhD degree in computer science and systems engineering from Yamaguchi University in 1999. He is presently an associate professor in the Faculty of Engineering, University of Miyazaki. His first interests lay in hydrodynamics and time series analysis, especially the directional wave spectrum. He is a theoretical computer scientist, and his current main research interests are automata theory, languages and computation. His articles have appeared in journals such as Information Sciences, Pattern Recognition and Artificial Intelligence, WSEAS, AROB, ICAROB, SJI, IEEE and IEICE (Japan), and proceedings of conferences such as Parallel Image Processing and Analysis, SCI, WSEAS, AROB and ICAROB.
He received his PhD degree in computer science and systems engineering from Yamaguchi University in 1999. He is presently an associate professor in the Faculty of Engineering, University of Miyazaki. His first interests lay in hydrodynamics and time series analysis, especially the directional wave spectrum. He is a theoretical computer scientist, and his current main research interests are automata theory, languages and computation. His articles have appeared in journals such as Information Sciences, Pattern Recognition and Artificial Intelligence, WSEAS, AROB, ICAROB, SJI, IEEE and IEICE (Japan), and proceedings of conferences such as Parallel Image Processing and Analysis, SCI, WSEAS, AROB and ICAROB.
Dr. Hiroshi Furutani
 He received his PhD of Science from Kyoto University in 1981. He is currently working in Innovative Computing Research Center at Doshisha University as researcher. His research interest includes bio-informatics, evolutionary computation and quantum computing.
He received his PhD of Science from Kyoto University in 1981. He is currently working in Innovative Computing Research Center at Doshisha University as researcher. His research interest includes bio-informatics, evolutionary computation and quantum computing.
Dr. Satoru Hiwa
 He received his PhD in Engineering from Doshisha University. He is currently working in Faculty of Life and Medical Sciences at Doshisha University, Kyoto, Japan, as an Associate Professor. His current research interests include human brain mapping, noninvasive neuroimaging and computational intelligence.
He received his PhD in Engineering from Doshisha University. He is currently working in Faculty of Life and Medical Sciences at Doshisha University, Kyoto, Japan, as an Associate Professor. His current research interests include human brain mapping, noninvasive neuroimaging and computational intelligence.
Dr. Tomoyuki Hiroyasu
 He received his doctor of Engineering from Waseda University in 1998. He has been a Professor of Life and Medical Sciences, Doshisha University, since 2008. His research interests include the development of novel evolutionary algorithms, medical image processing, medical information systems, parallel computing, Grid, web systems, and Intelligent systems. He is a member of IEEE, JSME, JSCES, IPSJ, SICE, and IEICE.
He received his doctor of Engineering from Waseda University in 1998. He has been a Professor of Life and Medical Sciences, Doshisha University, since 2008. His research interests include the development of novel evolutionary algorithms, medical image processing, medical information systems, parallel computing, Grid, web systems, and Intelligent systems. He is a member of IEEE, JSME, JSCES, IPSJ, SICE, and IEICE.
REFERENCES
Cite this article
TY - JOUR AU - Kenji Aoki AU - Makoto Sakamoto AU - Hiroshi Furutani AU - Satoru Hiwa AU - Tomoyuki Hiroyasu PY - 2019 DA - 2019/06/25 TI - Unified Approach to (1 + 1) Evolutionary Algorithm on Discrete Linear Functions JO - Journal of Robotics, Networking and Artificial Life SP - 56 EP - 59 VL - 6 IS - 1 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.190602.001 DO - 10.2991/jrnal.k.190602.001 ID - Aoki2019 ER -
