A Critique of Pandemic Catastrophe Modeling
- DOI
- 10.2991/jracr.k.191024.002How to use a DOI?
- Keywords
- Catastrophe modeling; pandemics; uncertainty; insurance; risk assessment
- Abstract
Catastrophe modeling is a popular risk assessment tool for the insurance industry and has been applied to a variety of natural disaster events. More recently, catastrophe modeling techniques have been extended to events, such as pandemics, where the range of possible scenarios is less understood due to the complexity of the hazard and the dependence of event magnitude to human response. Some general limitations of catastrophe modeling are discussed in the context of pandemics—such as the failure to distinguish natural variability from incertitude and the difficulty of ensuring a representative model—along with recommendations for minimizing surprises.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Over the past three decades, catastrophe modeling has become an essential tool of the insurance industry for estimating potential financial losses from disasters such as earthquakes and hurricanes [1]. The basic premise of catastrophe modeling is to combine stochastic hazard models with asset models to assess financial risk exposure from large events. While the original intent was to assess systemic risk, the influence of catastrophe models eventually expanded into related practical tasks—setting rates, allocating capital reserves, selecting markets, etc.
Considering the substantial variation in the nature of hazards, one would also expect considerable variation in the utility of catastrophe models depending on the availability of data and science. That is, more common events should generally yield more reliable projections. This requires a skeptical eye when evaluating new models, yet catastrophe models have become widely adopted and viewed as established (and therefore implicitly reliable) technology. It is normal to want to replicate success in one area to new situations. But the temptation to apply existing catastrophe modeling techniques to more uncertain events has gotten ahead of methodological development. The result is inevitable disappointment.
A prime example is pandemic catastrophe modeling where the hazard is a pandemic-inducing pathogen that results in substantial life and health insurance losses. While the insurance industry should be commended for tackling such an important topic, the uncertainties are daunting. The difficulty of quantitative pandemic risk assessment is summarized by Harvey Fineberg, the former president of the U.S. National Academy of Medicine, “Major flu pandemics arise on average only about three times every century, which means scientists can make relatively few direct observations in each lifetime and have a long time to think about each observation. That is a circumstance that is ripe for over-interpretation” [2].
Major limitations of hurricane catastrophe modeling—primarily in the form of hidden subjectivity—have already been well described [3]. Many of these limitations are generalizable to similar catastrophe models: flooding, earthquakes, etc., yet there is a new class of models with exceptional levels of uncertainty that require their own discussion. This critique explores the additional limitations unique to pandemic catastrophe modeling that further limit the value of these types of models for estimating financial exposure, disaster response, or social policymaking.
2. LESSONS FROM EBOLA
While pandemic catastrophe modeling has appropriately focused on avian influenza—the most likely cause of a pandemic—the current state of pandemic risk assessment can be evaluated using another recent deadly outbreak—the Ebola virus disease epidemic that emerged in West Africa in late 2013 [4]. Much like avian influenza, Ebola virus disease has zoonotic origins, but in this case the primary natural reservoir is bats rather than birds. In addition to the much higher mortality rate, Ebola is much less transmissible than influenza. These combined factors tend to limit outbreaks and the pandemic potential of Ebola is much lower than influenza [5]. Despite its more modest growth characteristics, Ebola outbreaks provide some insight into the current state of pandemic forecast modeling. During the Ebola outbreak, multiple epidemiological models (Table 1) that made short-range predictions in 2014 considerably overestimated its severity—some by an order of magnitude.
| Model | Timeframe (weeks) | Prediction | Actual (WHO data) |
|---|---|---|---|
| Total cases in Liberia | 10 | 9400–47,000 [6] | <7000 |
| Daily cases in Liberia | 15 | 249–545 [7] | <50 |
| Reported cases in Liberia | 12 | 20,471–94,143 [8] | 7819 |
| Total confirmed and probable cases | 6 | 5740 in Guinea | 1820 in Guinea |
| 9890 in Liberia | 4240 in Liberia | ||
| 5000 in Sierra Leone [9] | 4602 in Sierra Leone |
Accuracy of Ebola virus disease predictions made in late 2014
Unless the World Health Organization (WHO) underreported cases (which would be a separate serious problem in itself), the general inaccuracy of these predictions suggests that the progression of an epidemic is still difficult to model. Pandemics move quickly and the early stages are sensitive to assumptions regarding public health interventions. Likewise, failure to understand all the transmission routes (e.g., sexual transmission of Ebola by recovered patients) can make the end stages of a pandemic equally difficult to predict [10,11].
And it is not that the Ebola epidemic modeling was obviously too alarmist in overestimating the severity of the outbreak. For example, in July 2014, a Liberian man infected with Ebola flew to Lagos, Nigeria. If that case had not been quickly detected and contained, the epidemic could have entered a metropolitan area of 21 million people. Had that happened, the WHO mortality projections most likely would have been grossly underestimated. The difficulty is that these model estimates are strongly dependent upon many smaller events within the larger epidemic. One potential solution is to move toward agent-based modeling—computer simulations that estimate the aggregated consequences of the independent behavior of many individuals [12]. However, this approach is still very resource intensive, complex to build, and challenging to calibrate [13].
In addition, the translation of Ebola transmission risk studies performed in less-industrialized nations to more-industrialized nations presents a considerable challenge [14]. The response to the Ebola outbreak among the most industrialized nations was not uniform and there was even a noticeable difference in how scientists and public officials estimated risk. Because the transmissibility of Ebola is relatively low, medical experts recommended against the quarantine of U.S. medical workers returning from West Africa. However, the cost and effort of tracking and monitoring potential exposures led public officials to lean toward precautionary quarantines that varied from state-to-state. Estimating the human response is challenging and averaged data tell a very incomplete story. Any useful pandemic risk model would need to account for local and regional conditions that affect an outbreak’s progression.
The financial effects of a pandemic may be even more difficult to model. For example, the WHO’s estimate of the cost of controlling the West African Ebola outbreak jumped from less than 5 million USD$ in April 2014 to almost 1 billion USD$ in September 2014 [4,15]—an increase by a factor of 200 within 6 months. This demonstrates how difficult it can be to estimate the cost of a potential outbreak when it is not known at what stage the outbreak will be discovered or contained. The secondary economic impacts of a pandemic would also be expected to change rapidly and would need to include a range of extraneous factors that would only increase the uncertainty.
One might assume that after all the analysis of the West Africa Ebola outbreak [16], at least Ebola would now be easier to model. Yet the ongoing Ebola outbreak in the Democratic Republic of Congo (DRC) has been extremely difficult to predict. Initial opinion on the outbreak was cautious [17], but optimistic because the previous outbreak had made the world realize that Ebola was not just a self-limiting African disease, but had pandemic potential. Thus, the DRC’s prompt call for assistance and the faster WHO response—along with a new highly effective vaccine—all suggested rapid containment of the outbreak [18]. However, the outbreak has continued longer than expected due to multiple factors: persistent regional conflict [19], rampant disinformation [20], widespread use of inadequate health clinics [21], and even the limited availability of diagnostic tests [22].
The important lesson from this discussion of Ebola is that there is an extra layer of complexity inherent to pandemic modeling that is missing from most other natural disasters. The severity of damage from an earthquake is dependent on infrastructure built before the event, but the magnitude of the event itself is essentially independent of human activity. However, the magnitude of a pandemic is also dependent on the human response after the beginning of the disaster. Political inaction or inadequate public health systems will not make an earthquake larger, but can allow a small local outbreak to spread into a pandemic. Likewise, changing individual behaviors, such as increased social distancing or just more frequent hand-washing can substantially influence the progression of an infectious disease outbreak [23]. Because social conditions vary widely by region and can change unpredictably, a useful pandemic catastrophe model is much more difficult to construct than other natural hazard models. A realistic accounting of uncertainty in a pandemic risk model should show that our current incertitude is so large as to preclude standard probabilistic quantitative decision-making.
3. UNDERLYING PROBLEMS WITH CATASTROPHE MODELS
So, if we are asking too much of pandemic catastrophe modeling, what is wrong with the models and how do we fix them? The simple answer is that overconfidence in models is the underlying problem, but this overconfidence has some specific causes. The following outlines two of these problems and proposes mitigating actions.
3.1. The Mistreatment of Uncertainty
It is difficult to specifically critique commercially available pandemic catastrophe models because they are proprietary. However, the documentation for several hurricane catastrophe models is available for public inspection as a requirement of the Florida Commission on Hurricane Loss Projection Methodology. Given the basic similarities of catastrophe models, some general remarks can be made regarding their attempts to characterize uncertainty by aggregating scenarios through a large number of stochastic simulations. In these cases, the numbers of simulations or aggregation methods are not the issue, but the method of representing uncertainty.
There is no current consensus on the best way to represent uncertainty or when to use one form over another [24]. Furthermore, there is no consensus on the number of forms of uncertainty. Uncertainty has been categorized across a broad spectrum that ranges from certainty to nescience (unresolvable ignorance) [25]. Bayesians [26,27] generally argue that there is only one type of uncertainty—a measure of belief irrespective of its source—and that probability is the best way to express it [28]. At the other extreme, complex uncertainty typologies have been created that distinguish it by location, nature, and level with multiple subtypes [29,30]. The utility of this level of detail is debatable when there is no method for treating each distinct form of uncertainty [31,32].
While uncertainty representation is an unsettled matter, distinguishing between incertitude (i.e., lack of knowledge) and natural variability does have known advantages over a single treatment methodology. For example, when an analyst has no knowledge of the value of a parameter within a bounded range, it is common to represent that interval using a uniform distribution (a frequently used “uninformed prior” in Bayesian inference). However, treating interval data as uniform distributions requires an equiprobability assumption—an idea that traces back to Bernoulli’s and Laplace’s ‘principle of insufficient reason’ and more recently critiqued by Keynes under the name ‘principle of indifference’ [33]. Under this assumption, each possible value is considered to be equally likely and thus the interval can be represented by the interval’s midpoint—the mean and median of a uniform distribution. While the uniform distribution approach is computationally expedient and easy to understand, it can also disguise uncertainty. One result of the Central Limit Theory is that any distribution with finite variance, such as a uniform distribution, will converge to a normal distribution approximation when repeatedly convolved [34]. As shown in Figure 1, adding two uniform distributions results in a triangle distribution that would appear to have more certainty than the original uniform distributions. As the number of distributions increases, the resulting normal approximation does spread, but the assumed central tendency is maintained. By comparison, the addition of two intervals of [0, 1] by interval arithmetic yields the even wider interval [0, 2]. Repeating the process yields ever wider and more uncertain intervals without an artifact of precision.
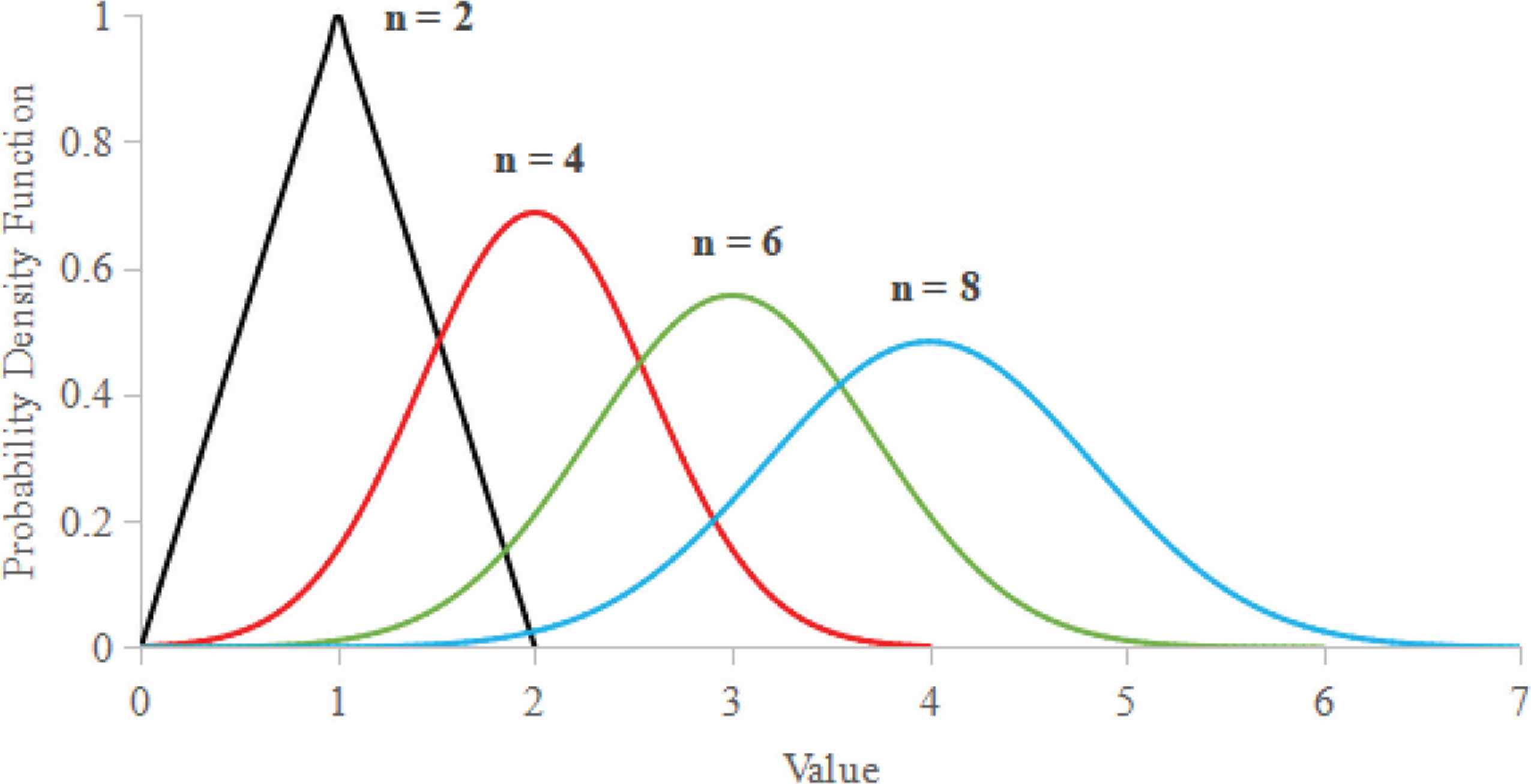
Convolution of n uniform distributions with bounds [0, 1].
The practical implication of this phenomenon is that standard Bayesian and Monte Carlo techniques have an important limitation. These approaches will yield valid results when the model inputs represent normally distributed natural variability. However, when the uncertainty due to lack of knowledge is large compared to the natural variability, the uncertainty in the model output will be under-represented. Unfortunately, this situation frequently occurs in rare natural disasters, such as pandemics.
In practice, uncertainty representation may be based on extraneous factors such as familiarity, academic tradition, or lack of knowledge of alternatives. Catastrophe modelers have been warned in the past to avoid becoming enamored with extreme precision that may not have a basis in reality [35], but they need further guidance. Fortunately, there has been considerable work in the area of intervalized probabilities [36,37], second-order Monte Carlo techniques, and robust Bayesian or Bayesian sensitivity analysis [38,39] which allows for the recognition of incertitude within Bayesian inference [36]. Models that more explicitly account for incertitude can sometimes yield results that seem disappointingly vague, but an honest portrayal of uncertainty is always informative.
However, catastrophe model users typically come from the world of financial modeling where data are abundant and historical prices are precisely known. It is not surprising that they prefer data analysis methods that are not optimal for addressing scenarios with sparse data and large incertitude. Adopting new methods may be a difficult transition despite their utility.
3.2. Failures of Imagination
In a workshop on the West Africa Ebola epidemic, virologist Daniel Bausch noted how prior relatively small outbreaks influenced expectations, “I think if you’d asked [Ebola virus experts] … a year and a half ago ‘Are we going to have 25,000 cases of Ebola in West Africa?,’ most of us would have not said that was a likelihood” [4]. It is common for modelers to claim that their models have been “validated” because they can replicate past data. However, this is history matching, not validation [40,41]. Acknowledging this distinction creates less surprise if we encounter extreme events not previously experienced or we discover that a model contains non-stationary processes that invalidate a model for future use. In terms of pandemic catastrophe models, diseases can behave unpredictably due to evolving pathogens or changing demographic conditions. For example, the 2017 outbreak of plague in Madagascar—normally a relatively controllable bacterial disease—was exacerbated by its spread to growing urban centers.
The user’s trust in any catastrophe model depends on assurances of validation (i.e., history matching) which may be acceptable in the case of relatively stable processes, such as earthquakes, but more tentative for pandemic catastrophe models that depend on non-stationary processes [42]. After catastrophic events, modelers have an opportunity to check their model against actual losses, so it’s not surprising that catastrophe model outputs will change after these recalibrating updates. However, it can be rather difficult to detect changes in the probabilities of extreme events caused by non-stationary processes [43].
One practical output of a catastrophe model is an exceedance probability curve, which summarizes the annual probability of exceeding particular losses—most importantly, a loss that would lead to the insolvency of an insurer. To generate these curves, catastrophe models will typically simulate many potential scenarios that include both historical data as well as scenarios that attempt to address limitations in the representativeness of the historical data set. This is especially necessary for models that include known non-stationary processes such as sea level rise, changing building technology, increased coastal development, etc. However, the Ebola epidemic serves as an example of a previously unforeseen risk that would not be captured merely by modestly expanding the range of a catastrophe model’s simulations.
Another lesson from the Ebola epidemic is that the various outbreaks within the larger epidemic had very different transmission dynamics depending on the level of cooperation and trust between the international public health workers, government officials, and affected communities. The impact of these social factors is critical to any risk assessment and difficult to characterize. Furthermore, new factors and previously unknown relationships in epidemic evolution are emerging as large epidemiological data sets are analyzed [44]. It would seem that a truly representative catastrophe model of a real-world epidemic would tend towards substantial complexity. One thoughtfully constructed pandemic catastrophe model [45–47] considers a myriad of factors including: wild and domestic viral reservoirs; the virulence and transmissibility of potential pandemic pathogens; the age and density distribution of populations; seasonal impacts; social factors such as air travel, work commutes and travel restrictions; and the availability of quality health care, antiviral medications, and vaccines. Whether these are enough factors is debatable. Estimating the insurance losses from a hurricane is fairly well-known and straightforward by comparison, yet building construction and risk mitigation details frequently ignored in standard catastrophe models can have a substantial impact on risk exposure estimates [48]. Furthermore, the impact, timing, and magnitude of each factor must be estimated along with any correlation with other factors.
In the end, we are left with the question of whether to pursue a more detailed pandemic catastrophe model that might be unusably complex or a simpler model that may be missing critical factors. There is a common, but often untested, assumption that complex problems call for complex solutions and that it is always better to use complex methods that make use of all available information [49]. However, there is a history of studies showing that very simple predictive models can often have better performance than complex models [50,51].
The question of best modeling approach has been explored in recent years in the epidemiological community in a series of infectious disease forecasting challenges [52]. For example, in 2015, the Research and Policy for Infectious Disease Dynamics (RAPIDD) Ebola forecasting challenge compared the predictive abilities of eight Ebola epidemiological models against a synthetic set of data over four scenarios at multiple points in an outbreak [53]. Models varied in complexity and ranged from 2 to 27 input parameters. The results did not point toward an “ideal” level of complexity because one of the best individual performers was a two-parameter stochastic model, while the worst performer was a two-parameter logistic growth model. The overall best performer was a Bayesian average of all the models which suggests that using multiple independent models is the current best approach. However, the last challenge scenario of an uncontrolled Ebola outbreak with noisy data was poorly predicted by all models, so even multi-model averaging has its limitations.
In a similar forecasting challenge for influenza in the U.S. over seven flu seasons, almost three-quarters of the 22 models evaluated made better seasonal predictions than the historical base-line model and the best performer was again a weighted combination of other models [54]. However, none of the models replicated the observed data more than 50% of the time and the challenge did not include an influenza pandemic—the models were optimized to predict seasonal flu.
Current epidemiological modeling for emerging infectious diseases tends toward using relatively simple models that only require the estimation of a few parameters primarily due to the scarcity of data [55,56]. More complex tools for assessing the pandemic risk of influenza [57,58] have not been widely adopted—one reason being their substantial data requirements.
Ultimately, choosing the level of model detail is a professional judgement in the art of modeling until the state of the art is improved. The current best solution to the problem of potentially non-representative data, processes or models is more attitudinal than technical. In the face of ignorance, the best approach is to use multiple competing models and constantly question their assumptions and results. In the case of epidemic modeling, real-time prediction remains a difficult challenge [59]. Furthermore, longer-term forecasting and predicting the emergence of new pathogens with pandemic potential will likely remain beyond our capabilities for the near future [60]. Given the dynamic nature of factors underlying epidemic progression, there may be limits on long-term predictability of infectious disease outbreaks and new analytical methods may be needed [61].
4. CONCLUSION
Catastrophe models can err in disaster forecasting for a variety of reasons. Here I have outlined one reason that is essentially an error of mathematical method and another based on an important psychological bias related to natural human optimism. However, there are others. For example, a pernicious cause of overconfidence in modeling is the human tendency toward excessive admiration of our own creations [62,63].
Ultimately, savvy users may know what level of confidence to put in their models, but shortcomings in current practices in uncertainty quantification require that model interpretation remain an art as much as a science until more progress is made. Although the focus of this discussion was pandemic modeling, catastrophe models are tackling other complex hazards with strong sociological components, such as cybersecurity and terrorism risks. Furthermore, standard catastrophe models are expanding into secondary areas such as business interruption losses [64]. Given the potential for overreach, catastrophe model users will need to practice shrewd professional judgment for some time to come.
Despite the critiques presented here, it is important to clarify that planning for disasters using data and quantitative methods remains an essential approach that can provide significant insight. While there is danger in putting too much confidence in a model’s results, failing to consider modeling at all presents the much larger danger of missing critical trends and vulnerabilities hidden within an overwhelming mountain of data. The only way forward is to keep improving the models while continuing to use them with a healthy skepticism.
CONFLICTS OF INTEREST
The author declare they have no conflicts of interest.
ACKNOWLEDGMENT
I would like to thank Sheldon Reaven for insightful questions and comments regarding this work.
REFERENCES
Cite this article
TY - JOUR AU - Daniel J. Rozell PY - 2019 DA - 2019/10/31 TI - A Critique of Pandemic Catastrophe Modeling JO - Journal of Risk Analysis and Crisis Response SP - 128 EP - 133 VL - 9 IS - 3 SN - 2210-8505 UR - https://doi.org/10.2991/jracr.k.191024.002 DO - 10.2991/jracr.k.191024.002 ID - Rozell2019 ER -
