Featured Hybrid Recommendation System Using Stochastic Gradient Descent
- DOI
- 10.2991/ijndc.k.201218.004How to use a DOI?
- Keywords
- Recommendation system; stochastic gradient; decent matrix factorization; content-based; collaborative filtering; incremental learning
- Abstract
Beside cold-start and sparsity, developing incremental algorithms emerge as interesting research to recommendation system in real-data environment. While hybrid system research is insufficient due to the complexity in combining various source of each single such as content-based or collaboration filtering, stochastic gradient descent exposes the limitations regarding optimal process in incremental learning. Stem from these disadvantages, this study adjusts a novel incremental algorithm using in featured hybrid system combing the feature of content-based method and the robustness of matrix factorization in collaboration filtering. To evaluate experiments, the authors simultaneously design an incremental evaluation approach for real data. With the hypothesis results, the study proves that the featured hybrid system is feasible to develop as the future direction research, and the proposed model achieve better results in both learning time and accuracy.
- Copyright
- © 2021 The Authors. Published by Atlantis Press B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Recommendation system is a branch of information filtering system that aims to predict “preference” or “rating” that a user prefers to give to an item (such as music, movies, or books) or social object (e.g. group or people) that had been unforeseen, using a model created based on the user’s social relationship (collaborative filtering model) or the features of an item (content-based model) [1,2].
Continuous growth of web and its applications has given a significant importance for recommendation systems [3]. However, recommendation system needs to deal with five main research problems: cold-start, data sparsity, accuracy and scalability [4].
Generally, there are three different groups of recommendation system: knowledge-based, Content-based (CB), Collaborative Filtering (CF) [2]. Consequently, these models use different sources of input data, and due to this difference, they all have different weaknesses and strengths. For instance, knowledge-based model can overcome cold-start problems better than CF or CB because they do not use ratings source. Contrarily, they are weaker than CF and CB in using information personalization from historical data [5]. These various personalities exhibited by different recommendation algorithms simultaneously figure out that recommendation model is not a one-size-fits-all model [6]. In another view, the recommendation algorithms themselves are considered as a part of system in giving the recommendations to users [7]. Such algorithms are efficient and simple; however, with the different data, they have limit in performance and it is not easy to further improve the accuracy of the recommendation system [8].
This is the reason why hybrid systems are the solution to explore these problems. However, the studies about hybrid system are still inadequate.
In this study, the authors design a hybrid system that combine CB and Incremental Matrix Factorization for the following reasons. First, CB and CF have different sources of data. The conjunction textual description of item in CB and community ratings in matrix factorization is expected to gain the accuracy in training data process. Second, almost all recommendation systems use numeric rating. Algorithms in incremental matrix factorization are considered in many researches for their benefit. Third, while most of the recent research focuses on algorithms for the basic model, few researches relate with the hybrid system and specific properties of evaluation real data unexplored [2].
In addition, this study aims to overcome the issues related to big data process. As mentioned above, the continuous growth of information, especially through the Internet, has given the issue related to the information overload. Netflix store over 17,000 movies in its data warehouse [9], and Amazon.com contains over 410,000 titles in its Kindle store. However, the speeds of computer is slower than the data sizes. Thus, regarding this issue, the capabilities of statistical machine learning algorithm are limited by the computing time rather than the data size [10].
To deal with this information overload, incremental learning algorithm is the effective solution with Stochastic Gradient Descent (SGD) algorithm [11]. However, the non-flexible feature in learning rate SGD require a better approach [2]. For this is reason, this study adjusts two mechanisms which are k group and momentum into novel algorithm – k Momentum SGD (KMSGD).
The final issue is how to evaluate in real data environment. While offline evaluation is suitable for achieving perspicuity about how different algorithms perform and comparing performance, it is limited in various ways [12,13]. In real data, evaluations need to be directly processed in every data point. This is not easy and comparing various algorithms through online evaluation is costly and difficult to synthetic enough understanding of these relationships [14]. In this study, the authors present a novel approach to evaluation in real-time by experimenting every point data separately.
Finally, the study aims to the following purposes:
- •
To enhance traditional recommendation system with better prediction and improve accuracy, we design a feature hybrid system combining the textual feature of CB and the robustness of matrix factorization in CF.
- •
To create a new incremental algorithm KMSGD that overcome the limit of SGD algorithm.
- •
To evaluate in stream data, we design a simple approach with every point data process.
By comparing with other recommendation algorithms on Movie-Lens data, it is verified that the traditional model performance can be effectively improved by our model in both accuracy and learning time. The featured hybrid system is appropriate to further develop in future.
The structure of this study is designed as follows. The study shows a broad overview of incremental learning algorithm before showing the detail process of SGD algorithm. Then the ideal to design KMSGD is described typically in incremental learning algorithms section. The development of algorithm in recommender systems from basic model, CF model with Matrix factorization algorithms to hybrid system is figured out in the development of model in recommendation systems section. Proposed model section give a specific description of model. Before discussing about the results in results and discussion section, the authors mention evaluation and data in evaluation issues and data section. The prequential evaluation protocol is also described in this section. Finally, conclusion section provides a brief conclusion about the study as well as the future works.
2. INCREMENTAL LEARNING ALGORITHMS
2.1. Incremental Learning
Traditional machine learning methods provide typically powerful method to give structural information from original digital data and almost all recent applications are restricted to the batch data. Training is applied for all given data. Consequently, model selection and evaluation measurement can be computed by this full data. The whole training process can understand that the data are static [2]. In contrast, incremental learning is considered to the position of continuous model adaptation which rely on a constantly coming data stream [15]. This process is always present whenever systems operate autonomously such as in autonomous house or driving [16–19]. Moreover, it is necessary to have an online learning in interactive perspective where training data rely on person feedback over time [19]. Finally, albeit static, that are almost digital data sets, can be so massive that they are de facto to tackle as a data stream, i.e. one incremental pass over the full data [2]. Incremental learning also figures out how to learn in such data streaming. It comes in different definition in the theory, and the utilization of the theory is not always suitable. Consequently, we present a meaningful definition to the appropriate terms of online learning, concept drift, and incremental learning, achieving typical attention to the supervised learning machine [2].
In the literature, there are a few researches on incremental CF. Incremental neighbourhood-based CF algorithm is applied [20,21]. For incremental matrix factorization, one first approach is designed [22], where the authors apply the fold-in method [23] to incrementally update to the factor matrices. An incremental learning algorithm for ranking source that utilizes a selective sampling approach is designed [24]. An incremental algorithm to update user factors is presented [25] by utilizing a simple method of the batch process. Two incremental algorithms using SGD are exposed [26]. This study is different from the above works. Stemming from SGD, we adjust the loop rate and momentum. Then, we design a novel evaluate method to evaluate the evolving accuracy of algorithm.
2.2. SGD Algorithm
2.2.1. The mechanism of SGD
Figure 1 present the mechanism of SGD [2]. Given a training dataset including data rows in the form 〈user, item, rating〉, SGD process various passes through the given data - iterations - until some stopping criteria is satisfactory – generally a convergence bound and/or maximum value of iterations [2]. At each iteration, SGD executes all observed ratings Rui and updates the correlative rows Wu and
Or with ϕ = (W; X), SGD contrarily process a parameter update for every training example x(i) and label y(i):

Algorithm 1-SGD.
In the training data, one major benefit of SGD is that complexity upgrades linearly with the number of observed ratings by getting benefit from the high sparsity of R [2].
Notably, after selecting a random training data point (i, j) ∈ D, SGD update Wi and Xj, and do not update factors for other training data point. This process savings follow process from representation of the global loss as a sum of local losses [27].
Thus, SGD refer to online learning or incremental gradient descent. In batched method, multiple local losses are averaged, and are also appropriate but usually have lower performance in experiment [2].
2.2.2. The limitation of SGD
In SGD, value of the learning rate (or step size) is very small α = 0.005. Consequently, a more suitable method to avoid local minimum and speed up convergence is to use the bold driver algorithm [28,29] to identify α in each iteration. Theoretically, it is feasible to use different step size for different factors [30].
An impressive method of these models is that executing until convergence for all iterations can lead to small worsening of the resolution quality of the unobserved value. Finally, it is usually reasonable not to set the convergence criteria too strictly [2].
Another key problem with SGD is about initialization. For example, it can begin the factor matrices to smaller values in (−1, 1). However, the choice of initialization, can alter the eventual solution quality.
2.3. Proposed Algorithm – KMSGD
2.3.1. Group in mini batch
Mini-batch gradient descent is an adjustment of the SGD that divides the training data into smaller groups that are utilized to identify model error and update model coefficients. Process may choose to compute the gradient over the mini-batch or take the average of the gradient which further decrease the variance of the gradient [2].
The ideal of method is illustrated in Figure 2. Mini-batch gradient descent aim to set a balance between the robustness of SGD and the speed-up of batch gradient descent. It is the most important process of gradient descent applied in machine learning.

Algorithm for KMSGD.
Figure 3 explains the algorithm 2 we propose [2]. According to it, this algorithm has two different things from algorithm 1-SGD. First, the learning process set a single pass over the observed data. Notable in algorithm 2, at each data point u, i, the alteration to factor matrices W and X are set in a single step. One other possible method is to perform several iterations over each new data point, with increasing accuracy, at the cost of the additional time required to re-iterate [2]. Second, there are no data shuffling or other pre-processing is processed. Thus, we set the error:

Algorithm 2 K-SGD.
There are two advantages in algorithm 2:
- •
To decrease the time of the parameter upgrade, which can aim to more suitable convergence.
- •
To make using of matrix optimizations machine learning that compute the gradient W.X.R. very effective.
2.3.2. Momentum
The name momentum stems from momentum in physics, wherein the weighted vector w, considered through a slight moving through parameter space, encounter acceleration from the gradient of the loss function [2]. Contrarily, traditional SGD is expected to keep moving in the same situation, preventing oscillations. Thus, momentum has been utilized effectively in studying artificial neural networks in recent years.
Momentum is a value that accelerate SGD in relevant direction and dampens oscillations [2]. This method utilizes a fraction of the vector vt of the previous-time step to the recent update vector:
The momentum term γ is set to 0:9 value. Basically, when momentum is utilized the process gains faster convergence and reduces oscillation. The mechanism of algorithm is illustrated in Figure 2 by adding vt in each iteration [2].
3. THE DEVELOPMENT OF MODEL IN RECOMMENDATION SYSTEMS
3.1. Single Model
In single model, algorithms play an important role and directly affect the performance of the recommendation system. The popular algorithms in recommendation can be divided into two main groups: CB model [31] and CF model [32].
3.1.1. Content-based
Content-based model utilizes features of users and items through the analysis of textual information, such as the features of items or user demography and document content to make recommendations. However, this feature extraction is difficult to gather or even fake; thus, this model has considerable limitations.
Figure 4 shows that the extraction the feature vector of item is the most important phase. Therefore, TF-IDF text mining algorithm is utilized in this study:
The loss function of content-base is presented as below:

Content-based.
In content-based model, the important step is to identify the typical feature of each item, which is a numeric vector record indicating the key features of item. For example, the featured vector includes the typical feature of the item that are easily identify. Such features include the characteristics of a movie that is relevant to system [2].
3.1.2. Matrix factorization
In Matrix factorization, the system that includes n users and m items, we correspondingly establish a matrix R with size (n × m), in which the (u, i)th entry is the rui value - the rating value of user u to item i [2].
In fact, R matrix with many empty cells-sparsity problem, is considered to overcome in recommendation system. Estimating unobserved ratings is also a necessary requirement [2].
The loss function of Matrix factorization is presented as below:
3.2. Hybrid System
Some recommendation systems combine various source aspects to create hybrid systems. Thus, hybrid systems can combine the strengths of different single model into unified system. Figure 5 shows three main ways of making hybrid recommendation systems [5]:
- 1.
Ensemble design: the output from single algorithm is combined into a robust output.
- 2.
Monolithic design: the combined recommendation algorithm is presented by using various data types.
- 3.
Mixed systems: these systems utilize multiple recommendation algorithms, but the items recommended by the several systems are unified system together side by side.
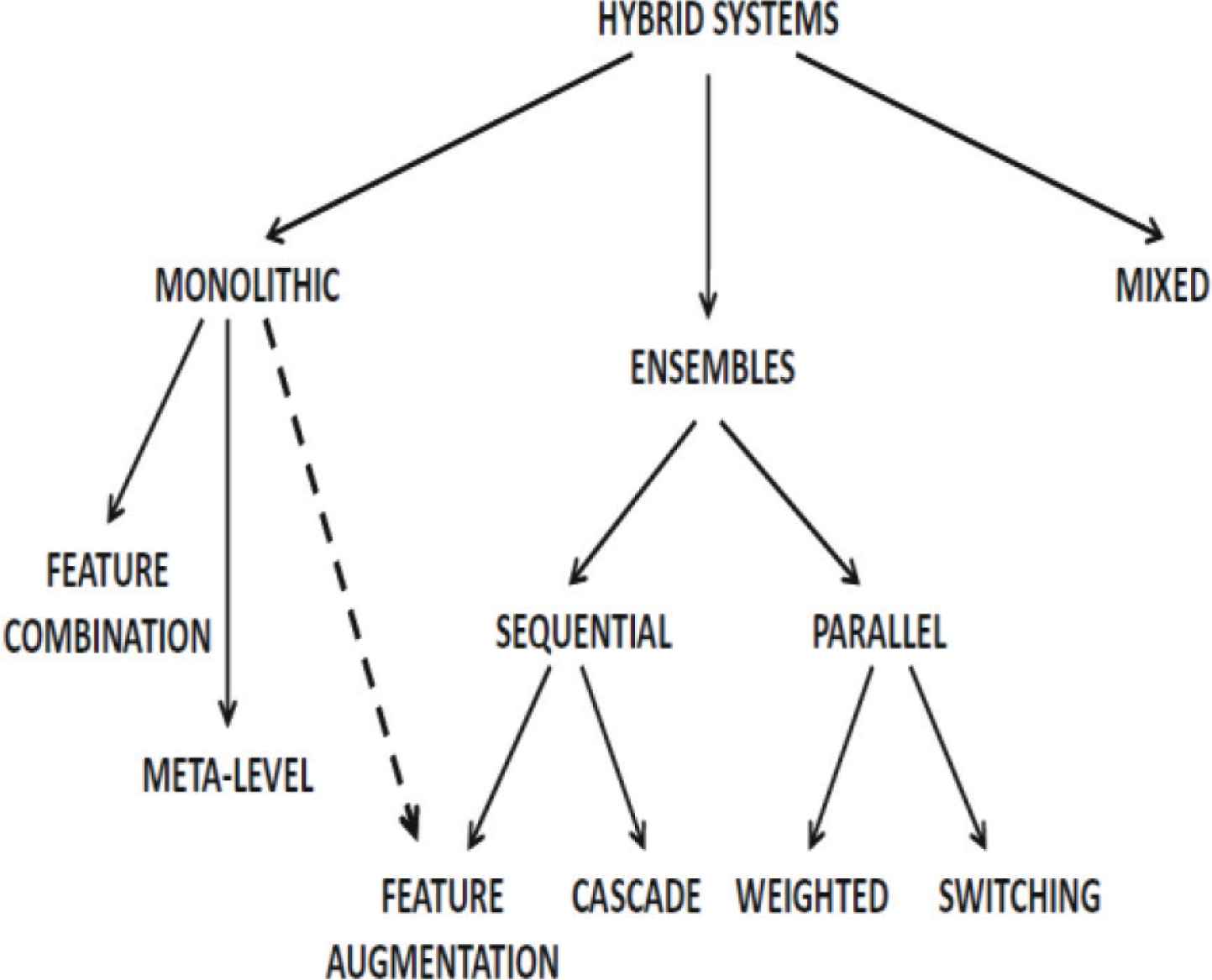
The taxonomy of hybrid systems.
Another way that hybrid recommender systems can be classified into the following categories (seven groups): weighted, switching, cascade, feature augmentation, feature combination, meta-level and mixed. Generally, this is the view with more detail than another one [33].
4. PROPOSED MODEL
4.1. CB and CF
As aforementioned, the CB and CF use various sources of input, and they have different strengths in different scenarios. Table 1 summaries the advantage and disadvantage between two these models.
| Categories | Collaboration | Input source | Advantage | Disadvantage | |||
|---|---|---|---|---|---|---|---|
| User | Item | ||||||
| Content-based | – | – | Textual description of item | • Item feature extract | • Non-collaboration | ||
| • Sparsity | • Cold-start | ||||||
| Collaborative filtering | Neighborhood-Based Collaborative Filtering (NBCF) | User–User | ✓ | – | Community ratings | • Simple | • Small Data |
| Item–Item | – | ✓ | • Easy to explain | ||||
| Model | ✓ | ✓ | • Cold-start | • Sparsity | |||
| • More accuracy | |||||||
Advantage and disadvantage of basis models in recommendation system
Generally, content-based with textual feature is to overcome the cold-start problem. However, it does not use the relationship among user or item. In contrast, collaboration is more robustness by using this relationship. This is the reason the hybrid system with various sources is expected to gain many opportunities to achieve the best results.
4.2. Feature Combine Hybrid System
Because CB and CF use different source, textual in CB and rating source in CF, the question is how to combine two model in to unify model before using training data.
Figure 6 present this idea.

Feature combine hybrid systems
Ratings matrix R with size (m × n) is added d columns for features of items. Thus, the new ratings matrix is set size (m × (n + d)), wherein d is the number of feature item and n is the number of items. Then the objective function is computed as follows with a parameter vector θ:
Notably, matrix R is an (m × n) latent ratings matrix, and C is a (d × n) content matrix, wherein each item is presented by d features. Examples include short reviews of items or properties of items. Since R is latent ratings matrix, missing values are set to be 0 value. Consequently, W is an (n × n) item-item coefficient matrix wherein the rating values are predicted as
subject to:
In a tuning phase, the weight parameter β can be determined. Although the rating values can be predicted either as
This approach can be utilized for combining any other instants of CF (optimization) model with CB models. For example, in the instant of matrix factorization, this method can use an (n × k) shared item factor matrix X, a (d × k) content factor matrix Z and (m × k) user factor matrix U to identify the optimization model as follows:
5. EVALUATION ISSUES AND DATA
5.1. Data
In the experiments, this study uses MovieLens-100M and MovieLens-100K which is presented in Table 2 to test hypothesis [2]. MovieLens-100K dataset includes about 943 users and 1.682 items with 100,000 rating values, and the dataset is download from the https://grouplens.org/datasets/movielens/ website. All the rating are from 1 to 5 value. MovieLens-1M dataset is also bigger with 1.000.209 ratings from 3.952 movies and 6.040 users. Notably, each user ranked at least 20 movies [2].
| Features | Data | |
|---|---|---|
| MovieLens-100 K | MovieLens-1 M | |
| Users | 943 | 6040 |
| Items | 1682 | 3952 |
| Ratings | 100,000 | 1,000,209 |
| Ratings per user | 106.4 | 165.6 |
| Ratings per item | 59.45 | 253.09 |
| Rating sparsity | 93.70% | 95.81% |
The statistics of the two datasets
5.2 Compare Methods
5.2.1. Evaluation measurements
We use Root Mean Squared Error (RMSE) value, which are commonly used in machine learning to evaluate the accuracy of model. The formulation is as follows:
The lower values of RMSE show the better prediction of the model.
The second measurements we use in experiment is learning time. This value is to evaluate the speed-up of learning algorithms.
5.2.2. Proposed evaluation method
To evaluate in incremental model, we design a prequential approach. Figure 7 shows the steps with every observed point data 〈u, i〉, presenting a rating interaction between user u and item i:

Real-data evaluation approach.
This approach provides following advantages:
- •
It allows management of incremental system.
- •
Offline evaluation can be integrated in online evaluation.
- •
Both new user and item instance is suitable to evaluation.
6. RESULTS AND DISSCUSION
The results of learning time and accuracy are presented in Tables 3 and 4 with the MovieLens-1M data and MovieLens-100K respectively. Moreover, the comparing average value among algorithms are shown in Figure 8.
| Measures | CB | Collaboration-Based-Filtering (CF) | Hybrid system | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Neighborhood-Based CF (NBCF) | Model-Based CF (MFCF) | Ensemble | Monolithic | ||||||
| User–User | Item–Item | ALS | SGD | KMSGD | Sequential | Parallel | Featured hybrid system | ||
| RMSA | 0.914 | 0.976 | 0.968 | 0.951 | 0.948 | 0.949 | 0.894 | 0.896 | 0.890 |
| Learning time (ms) | 0.886 | 1.186 | 1.166 | 1.986 | 0.118 | 0.101 | 0.108 | 0.106 | 0.104 |
Overall results of MovieLens-100K data
| Measures | CB | Collaboration-Based-Filtering (CF) | Hybrid system | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Neighborhood-Based CF (NBCF) | Model-Based CF (MFCF) | Ensemble | Monolithic | ||||||
| User–User | Item–Item | ALS | SGD | KMSGD | Sequential | Parallel | Featured hybrid system | ||
| RMSA | 0.916 | 0.975 | 0.966 | 0.944 | 0.940 | 0.936 | 0.912 | 0.918 | 0.910 |
| Learning time (ms) | 3.016 | 3.180 | 3.168 | 4.168 | 0.201 | 0.198 | 0.204 | 0.201 | 0.199 |
Overall results of MovieLens-1M data

Comparing average RMSA and time update value among algorithms.
6.1. About the Accuracy
Very impressively, the simple algorithm gains a best result with 0.914 in RMSA. In CF algorithms, the divergence is not significant and the KMSGD with 0.949 approximately same with 0.948 of SGD. However, the difference is highlighted in hybrid system group, especially featured hybrid system. If we only focus on CF algorithms [Neighborhood-Based Collaborative Filtering (NBCF) and Model-Based Collaborative Filtering (MFCF)], algorithm with SGD shows the best result. This means that the more complex model, the better performance recommendation system exception the impressive of CB. To explain this situation, the authors focus on data. In Movie-Lens data, the features of item are presented in 19 binary value (19 types of movies) with 1 for the kind of that type movie. TF-IDF algorithms become non-meaningful in extracting features in CB model.
For this reason, the same thing is proved with the 0.916 RMSA value of CB in Movie-Lens 1M.
However, featured hybrid system still gains the best value 0.910. It is assumed that, SGD algorithm is not much meaningful in predict model but the hybrid system is a best choice to recommendation system research.
6.2. About the Learning Time
The learning-time is the major part in this study. In big data, a power predicted systems become un-useful if they cost too much time to process. The hypothesis is that the more complex model, the slower in training data. This hypothesis is proved with the learning time value of CB, NBCF and ALS in MFCF with 0.886, 1.186, 1.166 and 1.986 ms respectively in MoviesLen-100K [2]. Very impressively, the algorithm with SGD, KMSGD and featured hybrid system is significantly better with 0.118, 0.101 and 0.104 ms respectively.
The results are the same with MovieLens-1M data. It means that the hypothesis the more complex model, the slower in training data is not correct. However, it became a big problem if we can use the incremental algorithm in model. It is proved with the Movie-Len 1M, the learning time of ALS compared with CB is significantly bigger: 4.168 and 3.016 ms. While the featured hybrid system continuously presents a lowest value with 0.199 ms.
Figure 8 presents a visual view about the comparing effectiveness among models. It can lead to conclusion that incremental algorithm and hybrid system deserve to depth research in recommendation system.
7. CONCLUSION
Stem from SGD algorithm, this study adjusts its mechanics in mini group and momentum. With experimental results, the proposed model combining feature of CB and the robustness of matrix factorization using incremental algorithm gain the better results in both learning time and accuracy with another state-of-the art algorithms. The contribute of study is also present in a novel evaluation approach in real data. Although this approach is still simple, at least it presents a novel direction research in recommendation system.
The limitations in this study is relevant to various data. In the real system, the data with new users, new item and ranking is continuously updated. Moreover, the evaluation approach in this study is just an initial idea for the power evaluation approach in the future.
In the future, the authors will consider to apply parallel and distributed data analysis. Furthermore, the hybrid recommendation system is also a highlighted research combined with deep learning algorithms such as the convolutional neural network and attempt to further develop their performance.
CONFLICTS OF INTEREST
The authors declare they have no conflicts of interest.
REFERENCES
Cite this article
TY - JOUR AU - Si Thin Nguyen AU - Hyun Young Kwak AU - Si Young Lee AU - Gwang Yong Gim PY - 2021 DA - 2021/01/05 TI - Featured Hybrid Recommendation System Using Stochastic Gradient Descent JO - International Journal of Networked and Distributed Computing SP - 25 EP - 32 VL - 9 IS - 1 SN - 2211-7946 UR - https://doi.org/10.2991/ijndc.k.201218.004 DO - 10.2991/ijndc.k.201218.004 ID - Nguyen2021 ER -
