On Learning Associative Relationship Memory among Knowledge Concepts
- DOI
- 10.2991/ijndc.k.200515.005How to use a DOI?
- Keywords
- Associative memory; knowledge concept relationship; memory optimization; knowledge network; dynamic reduction
- Abstract
A high-level associative memory modelling method was developed to explore the realization of associative memory. In the proposed method, two stage procedures are progressively performed to construct a unified associative knowledge network. In the first stage, some direct weighted associative links are created according to original context relations, and in the second stage, dynamic link reduction operations are executed to optimize associative access efficiency. Moreover, two kinds of link reduction strategies are designed including a global link reduction strategy and a dynamic link reduction strategy based on Hebb learning rule. Two independent datasets are considered to examine the performance of proposed modelling method. By means of reasonable performance indices, the experimental results displayed that, about 70% original links can be reduced almost without associative access failure but better total associative access efficiency. Particularly, the dynamic reduction strategy based on Hebb learning rule may achieve better associative access performance.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Knowledge graph is firstly put forward by Google in 2012 [1], which uses graph structure to represent knowledge information on conceptual items. In knowledge graph, each graph node denotes a knowledge concept, and edges equipped with labels represent semantic relations among knowledge nodes. Knowledge graph is a very useful tool to represent and store the information in natural language text, and has been widely and successively applied to natural translation [2], question-answer system [3], and natural language understanding [4].
For existing knowledge graph modelling techniques mainly including handcrafting rule methods [5], machine learning methods [6], and deep learning methods [7], they all consider that knowledge relationships among knowledge concepts are represented by semantic labels (like ‘belong to’, ‘is a’, ‘located at’ etc.). Obviously, these relationship labels play very important roles to accurately construct knowledge graph, and these labels should be carefully selected according to different concrete application scenes because the number of all possible labels should be very huge. In this study, we try to discuss another way of constructing knowledge graph that relationship label is discarded. Concretely, only one type of relationship among knowledge concepts, the associative relationship, is considered in this exploration research, which may form a unified complex network structure [8] like the structure of neural cells in human brain. In such knowledge graphs, we think that all semantic relationships are also represented by complex associative relationships among different object entities and semantic labels. Accordingly, those object entities and semantic labels are all uniformly considered as knowledge concepts. In addition, we call above knowledge graph structure as Associative Knowledge Network (AKN).
Along with above discussions, we will explore a kind of novel knowledge graph modelling methods. Wherein, network nodes may be knowledge concepts or semantic labels, and network edges denote unified associative relationships among network nodes. Moreover, the knowledge structure for a certain domain will be uniformly represented by edge weights same as associative weights among nodes. According to our knowledge, above research exploration has not been reported in existing public literatures.
When we model traditional knowledge graph, how to effectively construct model relationships from data sources should be a central work. Generally, there are much redundant knowledge information in original data material [9]. In order to get efficient knowledge graph model structure, many original knowledge relationships should be reduced or refactored. So, a two stages of modelling method are presented in this study. In the first stage, direct associative relationships are generated by analysing given text corpus. In this stage, all possible original associative relationships are extracted and stored. And then, link reduction stage is performed to optimize associative access efficiency. Furthermore, two plain link reduction strategies are newly proposed because of no existing reference. The one reduction strategy is global link reduction strategy for maximum associative weight reservation (named as global reduction strategy). Another strategy is dynamic link reduction strategy based on Hebb learning rule (named as Hebb reduction strategy), in which link weights can be dynamically updated in incremental way and incremental memory learning can be supported.
In addition, two associative access performance indices, associative computational efficiency and valid associative ratio of context knowledge concepts for give documents, are newly designed. Clearly, above two designed indices have believable physical meaning, and can give us effective reference to examine the model performance of constructed AKNs.
The remainder of the paper is structured as follows. In Section 2, background knowledge are described. Section 3 presents the detailed implementation of learning AKN and some theoretical analysis are given. In Section 4, two AKN examples are studied on food health and sport news respectively, and some interesting experimental results are reported. Finally, the main conclusions of our studies are stated in Section 5.
2. BACKGROUNDS
Generally speaking, the constructing procedure of knowledge graph includes following modules: information extraction, knowledge representation, knowledge fusion, and knowledge reasoning [10–15]. The first important part is information extraction, which is also the key step of knowledge modelling. For knowledge representation, the form of triple ‘entity–relationship–entity’ is usually adopted, which form is also used in this study. However, we try to introduce a unified relationship, associative relationship, to model knowledge graph, in which, pure associative relationships among knowledge concepts are considered.
For knowledge graph construction, its main task is to extract internal relationships among knowledge concepts. The early method of relationship extraction mainly used artificially constructed semantic rules and templates to identify relationships among knowledge concepts. Such methods seriously rely on artificial experiences. Thus, the rule or templates must be independently constructed for different technology domains and corresponding artificial workload will be very large. Further, many statistical machine learning methods are introduced to model and learn the relationships among knowledge entities by means of many supervised learning strategies. Wherein, some feature vector or kernel function based methods are developed. Liu et al. [16] proposed a new semantic kernel function constructing method using the ontology information provided by HowNet system, and corresponding relationship extraction accuracy can reach 88% for six kinds of entity relationships defined by Automatic Content Extraction (ACE) program on experimental open datasets. Although supervised learning methods can obtain good performance, however they require many artificial workloads of marking a large amount of corpus as training sets. Therefore, semi-supervised and unsupervised learning methods have begun to become new important research points. Carlson et al. [17] proposed a semi-supervised learning method based on Bootstrap algorithm, which can automatically identify the entity relationship. Zhang and Zhou [18] used an instance-based unsupervised learning method to obtain better experimental results on open corpus, and it can accurately identify multiple relationships among entities.
Nevertheless, they have a common feature for rules-based, supervised learning, and semi-supervised learning methods that all entity relationship types should be well pre-defined. Banko et al. [19] proposed an Open Domain Extraction (ODE) framework and published an open information extraction prototype system (Text Runner) based on self-supervised learning. Above system can use little supervised corpus as training dataset to obtain an entity relationship classification model, and then open data are classified to perform effective triple relationship extraction by means of Naive Bayesian model. Above system were effectively tested on large-scale real-world data, and its performance seems to be very good. In addition, we proposed a new knowledge recommendation method by directly constructing a similar relationship network on knowledge corpus [20]. Wherein, representation learning [21] and Google word2vec tool are used to get a word vector for each knowledge concept (a knowledge node in network), and then some most similar relationships are constructed for each knowledge node according to the Cosine distance among knowledge nodes with word vectors. For above proposed method, a very valuable knowledge recommendation procedure can be realized, and it can effectively improve the learning efficiency for individuals to grasp new domain knowledge.
3. MODEL METHOD
In this study, we mainly try to explore a novel knowledge network constructing method that the relationships among knowledge concepts are all uniformly denoted by associative relationships. Above consideration may be more similar to the thinking way in human brain, and corresponding research results could give us some useful inspiration for modelling more human-like knowledge representation models.
3.1. Associative Relationship Network
As well known, associative memory [22] should be a core function of human brain computation. Moreover, human brain learning should be looked as a complex associative memory process of generating, deleting, and updating neural information relationships [23]. If we introduce above idea to model associative relationships among knowledge concepts for a given corpus, we may think it should include two main stages. The one is to generate original associative links according to given documents, and another one is to refactor associative relationships in iterative learning processing. Wherein, reforming process will remove those redundant or low correlated relationship links to obtain higher access efficiency of associative memory.
In Figure 1, we give a demo about associative relationship network, in which a knowledge node denotes a concept word, directed links among concept words represent forward associative relationships. In the demo, all associative weights are not labelled.
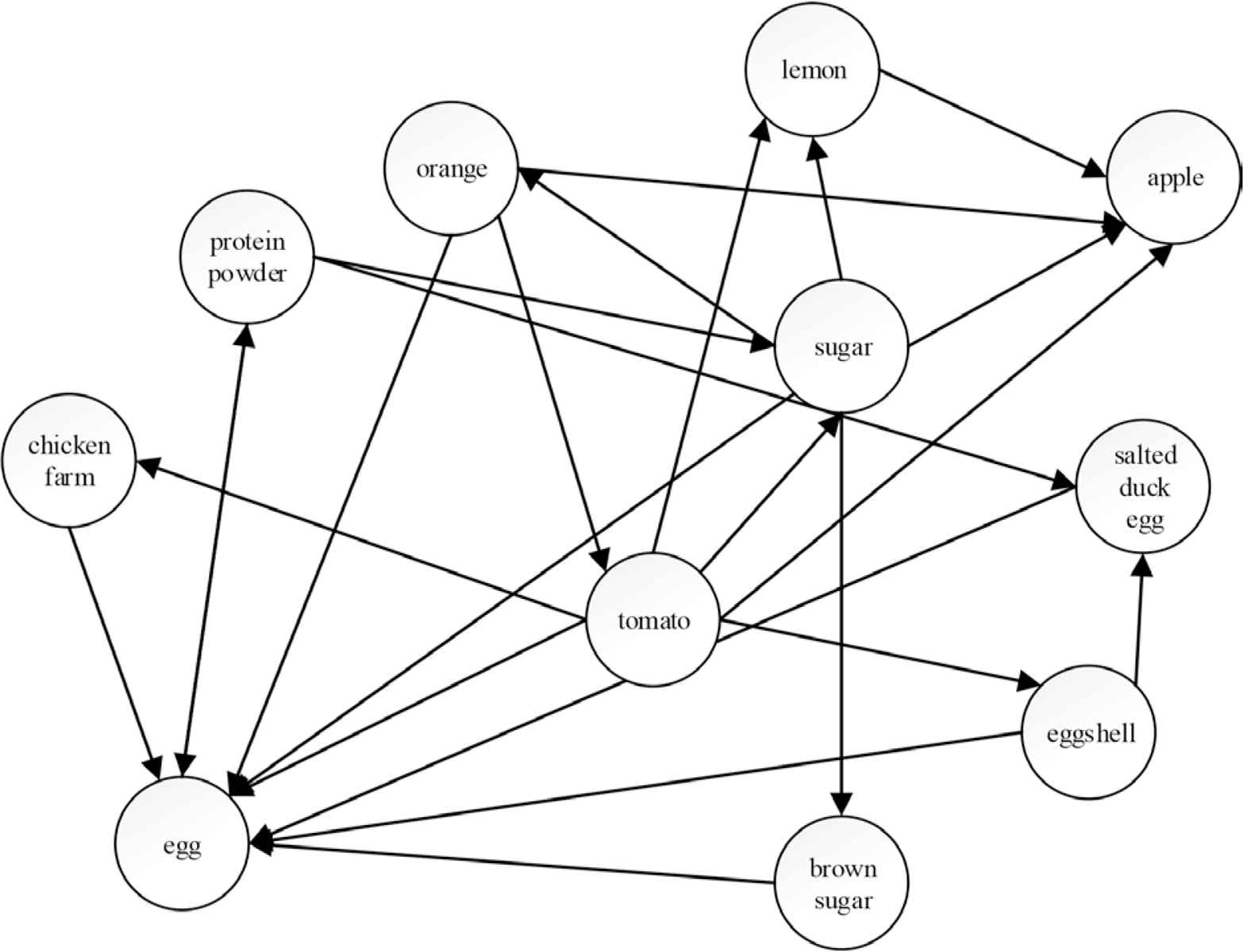
A part illustration of an associative relationship network.
According to above consideration, we use <a, b> to denote an associative relationship between concept words a and b. In this study, we will use document corpus as knowledge source, and the co-occurrence relationship among different knowledge concepts in a same sentence as original associative relationships. The proposed model includes two modules: a direct associative memory module, and an associative optimization module. Wherein, the direct associative memory module creates an initial associative knowledge network from given document corpus by knowledge concept word extraction, and co-occurrence relationship intensity computation. The associative optimization module mainly removes some low-intensity associative relationship links and adjusts some intensity values of retained associative relationship links. The main objective of associative optimization is to improve the computing efficiency of associative access for extracting correlated knowledge concepts.
3.2. Initializing AKN
For constructing initial AKN, three steps are considered. At first, all useful knowledge concept words should be extracted using existing related methods. Then, the co-occurrence relationships among those knowledge concept words are analysed. Here, we assume that, if two concept words appear in a same sentence, then we think that they may generate one time of co-occurrence. Moreover, we consider corresponding associative relationship is <a, b> if a is in front of b in a same sentence. Concretely, relationship weights for two co-occurrence concept words are evaluated according to their position distance in a same sentence.
In order to initialize associative weights, we first think that the associative intensities between two concept words should mainly depend on the number and position distances of their all co-occurrence. So, we introduce a following definition for computing original associative weights.
Definition I:
For two knowledge nodes Sa and Sb in an AKN, their original associative weights Uab is computed according to the following Equation (1).
In above equation,
3.3. Associative Relationship Reduction
Inspired by the idea of associative memory in human brain neural system, we think that initial AKN also should be reformed to improve the associative performance. Obviously, any knowledge node should not be deleted in reforming stage. So, the main processing in this stage is to remove some associative links and to adjust corresponding associative weights. For above problem, few methods are reported in existing research, and several related studies include: Liu etc. [24] presented a ‘feature dimension reduction’-based text topic representation model on complex network, in which networks are reduced by constructing multi-level feature words. Subbian et al. [25] studied the theory of information spreading in social networks, and presented a greedy searching strategy to access the most closely related entity node for given information flow. This study may give us some enlightenment to exploit possible network reduction methods. Rosenberg [26] proposed a maximum information entropy coverage model to improve the efficiency of computing information dimension, in which a new information dimension computation was introduced.
According to above discussions, we introduce two reduction methods to study how to optimize associative memory access in an AKN. The first method is a global associative memory maximum preservation algorithm. Its main processing is that, all associative links are considered to be removed if their initial associative weights are less than a threshold θ. Obviously, above strategy is a very simple method and cannot support incremental link reduction, and it certainly do not accord to the mechanism of human associative memory learning. In this study, we mainly use this method as a basic reference because there is no other existing method according to our investigation.
The second associative relationship reduction method is Hebb learning rule based dynamic reduction method. In this method, all learning documents can be incrementally afforded. And for each batch of incremental documents, the Hebb rule is used to update corresponding associative weights. Wherein, one time of associative link reduction processing is performed after every batch of learning. Hebb learning rule was put forward by Donald Hebb to explain the learning processing of biological neurons when they are continually stimulated by learning signals. Concretely, it assumes that the associative weight between associative nodes should be accumulatively enhanced if this associative link is continually activated. So, we may introduce following equation to update corresponding associative weights.
In addition, we consider that for every knowledge node its total forward associative ability can be normalized to be one. That is, after associative weights updating of tth batch of learning, we perform following computation.
According to the above discussions, we may give following procedure for Hebb rule-based associative knowledge relationship reduction method.
| Hebb rule-based associative knowledge relationship reduction method | |
|---|---|
| Input | A batch of documents {DSi}i=1...n; an empty network structure G = (V, E, U) a combination of a knowledge node set, associative edge set, and an edge weight set; a weight threshold θ, indicator variable i = 0. |
| 1 | Initialize G1 using DS1 according to the description in Subsection 3.2 and network structure G. |
| 2 | Generate a G′ = (V′, E′, U′) using DSi according to the description in Subsection 3.2 and network structure G. |
| 3 | Initialize an empty Gi+1 = (Vi+1, Ei+1, Ui+1), and let Vi+1 = Vi ∪ V′ and Ei+1 = Ei ∪ E′. |
| 4 | For all
|
| 5 | Re-normalized all
|
| 6 | If the learning procedure is completed then go to next step, otherwise let i = i + 1 and go to step 2. |
| 7 | Output the final AKN Gi+1. |
| 8 | END |
For the learned AKN, the associative access can be executed on the corresponding graph structure. Moreover, we may consider that, the associative access can be extendedly executed across multiple sequential associative links. Of course, we also think that multiple associative access should spend more computing cost. This will be further discussed in our experimental analysis.
4. EXPERIMENTAL ANALYSIS
4.1. Experimental Methods
Based on the problem considered in this study, we constructed two datasets by crabbing public text data in Internet. Concretely, Dataset I was constructed by gathering a group of popular science articles on the topics ‘healthy knowledge’, ‘dietary nutrition’ and ‘dietary errors’ from websites Meishi-Baike [27] and FoodBK [28]. In Dataset I, the total number of articles is 6242. For Dataset II, we collected 1953 news pages on the topic of sports from a standard dataset ‘Sohu News Data’ provided by Sogou Lab [29], and these news pages were from the Sohu sports [30].
For the knowledge graph modelling problem, it is very important of evaluating the quality of modelled result. In general, F-value performance index could be used for supervised or semi-supervised learning problem, but for unsupervised modelling learning problem there is no common evaluation index [31]. For some clustering problems, normalized mutual information may be used [32]. So, we designed a new unsupervised modelling evaluation index, associative efficiency, to examine the performance of our model.
At first, we introduce an associative cost value for once associative access on AKN, and it can be defined as follows.
Definition II:
For an associative access sequence SQ = <v1, v2,..., vm> on an AKN G = (V, E, U), we define its associative access cost Cac(SQ) as,
For above definition, it is inversely proportional to normalized associative weights and has additivity property. We think that, above consideration should be reasonable by comparing the associative processing of human brain. That is, when we consider the space of containing neurons and their links is limited, then in order to get optimal associative memory performance for given memory task, the associative weights should be different for different associative links. Moreover, the basic computing ability of each neuron may be supposed to be equal.
If above definition is designed, we may further introduce the definition on associative access cost for any two knowledge nodes vi, vj
In practice, we will limit the search length of possible SQ for computing feasibility, and the maximum possible length is set as 7 in our experiments. If no possible associative sequence is found for two expected access nodes vi, vj, then we say they are unreachable on given AKN.
Furthermore, we can propose an associative understanding cost for a given reading document D.
In above equation, Sent(D) denotes the set of all sentences in document D, <vi, vj> represents an adjacent knowledge word pair in a sentence, and Zv(D) represents the number of all valid associative access for all adjacent knowledge word pairs. So, we can introduce another performance index, the ratio of valid associative access.
According to above two performance indices, we can effectively evaluate the quality of an AKN. If two AKNs have same Rvac values, then an associative understanding cost is lower, the corresponding AKN is better. In addition, we can compute the average values of Cau and Rvac as performance indices for a document set.
4.2. Experimental Results
For above two datasets, we use our modelling methods to construct corresponding AKNs. In order to compare model performance in different link reduction degrees, a group of experimental tests are performed for each dataset, and corresponding experimental results are reported in Tables 1 and 2 respectively for Dataset I and II. Wherein, 10 levels of reduction degrees are considered by adjusting associative intensity threshold θ. Accordingly, relative average Cau and Rvac values by global and Hebb reduction strategies are recorded. Besides, the optimal average Cau values obtained by global and Hebb reduction on different reduction ratios are bold in Tables 1 and 2.
| Reduction ratio (%) | Relative average Cau by global reduction | Relative average Cau by Hebb reduction | Average Rvac by global reduction (%) | Average Rvac by Hebb reduction (%) |
|---|---|---|---|---|
| 0.00 | 1.000 | 1.000 | 100.0 | 100.0 |
| 3.42 | 0.969 | 0.952 | 100.0 | 100.0 |
| 15.74 | 0.864 | 0.799 | 100.0 | 100.0 |
| 32.83 | 0.688 | 0.667 | 100.0 | 100.0 |
| 47.66 | 0.612 | 0.553 | 99.98 | 100.0 |
| 59.20 | 0.404 | 0.321 | 99.77 | 99.89 |
| 76.61 | 0.214 | 0.154 | 98.33 | 99.51 |
| 83.40 | 0.527 | 0.287 | 96.47 | 99.02 |
| 88.90 | 1.109 | 0.944 | 94.21 | 97.13 |
| 91.40 | 1.513 | 1.117 | 91.19 | 94.67 |
The modeling performance on Dataset I
| Reduction ratio (%) | Relative average Cau by global reduction | Relative average Cau by Hebb reduction | Average Rvac by global reduction (%) | Average Rvac by Hebb reduction (%) |
|---|---|---|---|---|
| 0.00 | 1.000 | 1.000 | 100.0 | 100.0 |
| 8.41 | 0.521 | 0.509 | 100.0 | 100.0 |
| 17.60 | 0.440 | 0.426 | 100.0 | 100.0 |
| 23.32 | 0.405 | 0.376 | 100.0 | 100.0 |
| 31.30 | 0.349 | 0.294 | 99.97 | 100.0 |
| 45.31 | 0.317 | 0.274 | 98.77 | 99.81 |
| 63.70 | 0.293 | 0.238 | 98.43 | 99.04 |
| 77.28 | 0.238 | 0.189 | 98.11 | 98.68 |
| 83.10 | 0.532 | 0.529 | 97.68 | 98.05 |
| 92.50 | 1.166 | 0.955 | 94.51 | 96.36 |
The modeling performance on Dataset II
For reduction ratio in Tables 1 and 2, we examine 10 levels mainly by adjusting threshold θ in Hebb reduction strategy and then adjusting threshold θ in global reduction strategy to fit to the corresponding reduction ratio. In addition, for the convenience of comparison, we set relative average Cau value as 1.000 for the case with no link reduction. Accordingly, if the relative average Cau value is <1, then it shows better associative computing efficiency, inversely, it will be worse performance.
According to the results in Tables 1 and 2, we can find that, relative average Cau values decrease at first with the increase of reduction ratio, and then may exceed 1 after reduction ratio more than a critical value. Above phenomena may indicate that associative link reduction could be very meaningful for neural associative learning. Furthermore, appropriate reduction should be very important for optimal associative memory learning. Above results demonstrate that some original associative links with low associative intensity values might be removed and their associative access can be realized according to multiple indirect associative access, thus the total associative access cost can be lower.
Furthermore, average Rvac values on two datasets and two reduction strategies go down slowly with the increase of reduction ratio in Tables 1 and 2. Specifically, average Rvac values can keep almost 100% if reduction ratio is not very high. These results seem to be very interesting on associative relationship memory among knowledge concepts.
In addition, we may find that in all experimental cases, the reduction ratio cannot be raised to a very high value. Excessive link reduction will result in relatively worse associative access performance than original direct memory. This result is also a very interesting phenomena that may give us some inspiration to exploit human associative learning mechanism. For example, our experiments on associative memory using computing simulation may uncover that, a certain amount of neural links should be inevitable to achieve high associative access efficiency when human brain memorizes a complex knowledge system.
For Hebb reduction strategy and global reduction strategy, although they display similar performance features on two different datasets, but Hebb reduction strategy shows obviously better algorithm performance. Hebb reduction strategy can not only be suitable for the requirement of incremental learning which is unavoidable in practice, but also achieve better associative efficiency and higher associative accessibility.
Another result can be concluded from Tables 1 and 2 is that, the optimal reduction ratios are all in 70–80% for two experimental datasets and two compared algorithms. And above range seems to be independent to datasets themselves according to some extra experiments, for example we select subsets of Dataset I as learning datasets. Wherein, the relative associative access efficiency may be raised to about five times of original memory access efficiency.
In summary, above results seems to be very accordant to our common sense on associative memory learning features of human brain, which also reflect the reasonability of our two newly introduced computing definitions of evaluating associative modelling and access efficiency. Nevertheless, this study only gives some preliminary results on the viewpoint of learning high-level associative memory among knowledge concepts. Human brain is a very complex cognitive processing system, the true mechanism of associative memory constructing procedure in human brain should be far more than the considerations in this study, and we will also constantly exploit its secret.
4.3. Case Analysis
In this subsection, we will give some concrete cases to illustrate the changing difference of associative access path between original memory and reduction memory. Tables 3 and 4 show a group of associative access cases respectively on Dataset I and II, in which associative access cost Cau is listed before and after link reduction processing.
| Case 1 | Case 2 | Case 3 | |
|---|---|---|---|
| Associative relationship | [Laiyang pear, lotus nut] | [Mulberry, diabetes] | [Medlar, red jujube] |
| Cau value with no link reduction | 8.263 | 11.572 | 2.759 |
| Associative access path after Hebb reduction | [Laiyang pear → snow pear → vitamin → lotus nut] | [Mulberry → carotene → carrot → newtol → diabetes] | [Medlar → red jujube] |
| Cau value after Hebb reduction | 6.011 (1.913 + 1.886 + 2.212) | 7.078 (1.516 + 1.733 + 1.891 + 1.938) | 1.526 |
Three associative access cases on Dataset I
| Case 1 | Case 2 | Case 3 | |
|---|---|---|---|
| Associative relationship | [Winger, head coach] | [Xiexia Chen, barbell] | [Ming Yao, Houston Rockets] |
| Cau value with no link reduction | 6.457 | 7.849 | 1.624 |
| Associative access path after Hebb reduction | [Winger → Arsenal → Emery → head coach] | [Xiexia Chen → women’s football → barbell] | [Ming Yao → Houston Rockets] |
| Cau value after Hebb reduction | 4.928 (1.705 + 1.593 + 1.63) | 5.265 (3.418 + 1.847) | 1.015 |
Three associative access cases on Dataset II
From the results in Tables 3 and 4, we may find that, for some direct relationship links with low associative intensity values (high Cau values) in original AKN, they may be more effectively accessed even though multiple indirect associative access is required. That is to say, if some original associative links with low intensity values are removed, then those retained links will own lower associative access cost. Moreover, it is possible for those links that were removed, they may be indirectly accessed with lower total associative cost.
Nonetheless, it should be pointed that, link reduction will delete some part of original semantic correlation. For example, the Case 1 in Table 4, associative relationship [Winger, head coach] may directly reflect Winger is a head coach. But for corresponding associative access path after Hebb reduction, [Winger → Arsenal → Emery → head coach], the semantic relationship between Winger and ‘head coach’ may not be obviously understood. So, how semantic relationships are effectively represented in a pure associative knowledge network should be further studied.
5. CONCLUSION
In this study, a new exploration on modelling associative relationship memory among knowledge concepts was performed. Wherein, a novel associative link reduction strategy based on Hebb learning rule was proposed to optimize associative relationship memory. Our experimental results clearly show moderate link reduction can achieve markedly better associative efficiency than direct associative memory. And Hebb rule-based link reduction can be very effective not for high associative efficiency but for incremental learning ability. In addition, we also find that, for a certain knowledge corpus, a certain amount of associative links should be necessary for effective associative access and high computing efficiency.
The experimental results reported in this study will provide some new thinking for constructing human-like associative knowledge memory system. Our proposed modelling method may also be valuable for associative information retrieval, knowledge recommendation and knowledge graph construction. Furthermore, how to effectively represent complex semantic relationship among knowledge concepts in a pure associative knowledge will be our next research work.
CONFLICTS OF INTEREST
The authors declare they have no conflicts of interest.
ACKNOWLEDGMENTS
This work was mainly supported by
REFERENCES
Cite this article
TY - JOUR AU - Zhenping Xie AU - Kun Wang AU - Yuan Liu PY - 2020 DA - 2020/05/27 TI - On Learning Associative Relationship Memory among Knowledge Concepts JO - International Journal of Networked and Distributed Computing SP - 124 EP - 130 VL - 8 IS - 3 SN - 2211-7946 UR - https://doi.org/10.2991/ijndc.k.200515.005 DO - 10.2991/ijndc.k.200515.005 ID - Xie2020 ER -
