A Novel Hybrid Cuckoo Search Algorithm with Global Harmony Search for 0–1 Knapsack Problems
- DOI
- 10.1080/18756891.2016.1256577How to use a DOI?
- Keywords
- Cuckoo search; Global Harmony Search; 0–1 knapsack problems; Hybrid Encoding
- Abstract
Cuckoo search (CS) is a novel biologically inspired algorithm and has been widely applied to many fields. Although some binary-coded CS variants are developed to solve 0–1 knapsack problems, the search accuracy and the convergence speed are still needed to further improve. According to the analysis of the shortcomings of the standard CS and the advantage of the global harmony search (GHS), a novel hybrid meta-heuristic optimization approach, called cuckoo search Algorithm with global harmony search (CSGHS), is proposed in this paper to solve 0–1 knapsack problems (KP) more effectively. In CSGHS, it is the combination of the exploration of GHS and the exploitation of CS that makes the CSGHS efficient and effective. The experiments conducted demonstrate that the CSGHS generally outperformed the binary cuckoo search, the binary shuffled frog-leaping algorithm and the binary differential evolution in accordance with the search accuracy and convergence speed. Therefore, the proposed hybrid algorithm is effective to solve 0–1 knapsack problems.
- Copyright
- © 2016. the authors. Co-published by Atlantis Press and Taylor & Francis
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Optimization problems can be found in various fields in the real world, such as engineering, manufacturing, finance, medical science, music and so on. More generally, the process of optimization is to find the best possible solution of some objective function in a given domain. Unfortunately, it is difficult for the traditional methods to cope with some high-dimensional, non-differentiable, discontinuous complicated problems. Under these circumstances, meta-heuristic techniques begin to show their powerful search ability.
Some of them include ant colony optimization (ACO) 1, bat algorithm (BA) 2, bacterial colony foraging (BCF) 3, bird swarm algorithm (BSA) 4, chicken swarm optimization (CSO) 5, differential evolution (DE) 6–7, firefly algorithm (FA) 8–10, krill herd algorithm (KH) 11–18, monarch butterfly optimization (MBO) 19–21, particle swarm optimization (PSO) 22–23, earthworm optimization algorithm (EWA) 24 and elephant herding optimization (EHO) 25–26. These algorithms have been used to successfully address many complicated engineering problems, such as ordinal regression 27, classification 28, data encryption 29, possession 30, scheduling 31, test-sheet composition 32, target assessment 33–34, path planning35–37, directing orbits of chaotic systems 38, feature selection39, and fault diagnosis 40.
Cuckoo Search (CS) is one of the latest nature-inspired meta-heuristic algorithms developed by Yang and Deb 41. CS is based on the brood parasitism of some cuckoo species by laying their eggs in the nests of other host birds. In addition, this algorithm is enhanced by Lévy flights, rather than by simple isotropic random walks 42.
Harmony Search (HS) is a relatively novel music-inspired metaheuristic optimization algorithm developed by Geem et al. 43. It mimics the music improvisation process where musicians improvise their instruments’ pitches striving to find pleasant harmony-it is like that the optimization method searches for the global optimal solution. Owing to its potential as an optimization technique, it has gained considerable attention and many variants are proposed to enhance the performance of HS 44–46. Mahdavi et al. 47 proposed the improved version of harmony search algorithm (IHS) which dynamically updates the values of the pitch adjustment rate (PAW) and the pitch adjustment bandwidth (BW). Due to the fact that BW in IHS is difficult to guess and problem dependent, inspired by the concept of swarm intelligence as proposed in PSO, Omran and Mahdavi 48 proposed the global harmony search (GHS) algorithm.
Owing to the significant features such as fine balance of randomization and intensification and fewer number of control parameters 41, CS is becoming a new research hotspot in swarm intelligence and various variants have emerged in large numbers with an intension to further enhance the optimization ability. Walton et al. 49 developed a modified cuckoo search algorithm for solving nonlinear problems. Yang and Deb 50 extended it to multiobjective optimization problems. Yildiz 51 successfully used CS to select optimal machine parameters in milling operation and proved that was more effective. Ouaarab et al. 52 proposed a discrete cuckoo search to solve traveling salesman problem. Li et al. 53 introduced an adaptive parameter CS for global numerical optimizatioin. Recently, hybridization that CS in combination with other methods has been proposed and has become ever-increasing hot topics studied by people, such as CS combined with orthogonal learning strategy 54, shuffled frog leaping algorithm (SFLA)55, wind driven optimization (WDO) 56, artificial neural network (ANN)57 and genetic algorithm (GA)58. For details, see 59.
Some researchers attempt to solve knapsack problem (KP) problems by CS. In 2011, Layeb 60 proposed a hybrid optimization algorithm which combined cuckoo search and quantum-based approach to solve knapsack problems efficiently, and afterward, Gherboudj et al.61 conducted research on knapsack problems with purely binary cuckoo search. The research on knapsack problem based on CS is not enough. Additionally, although many efficient methods have emerged for the 0–1KP problems 62–63, in fact, further work is needed to resolve some new and harder 0–1 knapsack problems hidden in the real world, or rather, the correlation between the weight and the profit of the items may not be more concerned. In 62–63, although 10 low-dimensional and 16 randomly-generated high-dimensional 0–1KP instances are used, the latter did not consider the correlation between the profits and weights of the items. As a result, it has a wider significance to explore some new approaches to handle the 0–1 knapsack problem.
There are some studies on hybrid harmony search and other methods, like the combination of harmony search and firefly algorithm 64, cuckoo search algorithm 65, but most of the hybridization is adopted the standard harmony search which has some shortcomings. The parameters are difficult to adjust, for example.
Based on the above analysis, we propose a novel hybrid optimization algorithm by integrating the global harmony search into the cuckoo search algorithm for solving 0–1 knapsack problems. To demonstrate the efficiency of the proposed method, a large number of experiments on 0–1 knapsack problems with six groups of instances are carried out. The experimental results show that the proposed hybrid metaheuristic method can reach the required optima more effectively than CS, SFLA, and DE, even in some cases when the problem to be solved is too complicated and complex.
The rest of paper is organized as follows. Section 2 introduces the preliminary knowledge of CS, GHS and the mathematical model of 0–1 knapsack problem (0–1KP). Then, our proposed CSGHS for 0–1 KP problems is presented in Section 3. A series of simulation experiments are conducted in Section 4. Some conclusions and comments are made for further research in Section 5.
2. Review of the Related Work
In this section, the definition and mathematical model of 0–1 knapsack problems are outlined as well as the basic CS and GHS.
2.1. 0–1 knapsack problem
0–1KP is one of the most intensively studied combinatorial optimization problem 66. The researches of 0–1 knapsack problem have very large potential application background for capital budgeting problems, resource allocation, loading problems, project selection problems and so on 67. The 0–1 knapsack problem can be generally described as follows: Given N objects, from which various possible objects will be selected to fill up a knapsack. Then, if pj is a measure of the value given by object j, wj its weight and c the capacity of the knapsack. The objective is to maximize the total value of the knapsack that the knapsack capacity constraint is satisfying. Formally, the problem can be formulated as follows:
2.2. Cuckoo search
CS 41 is one of bio-inspired algorithms for imitating the brood parasitism of some cuckoo species. Because of the complexity of natural systems, they cannot be built models exactly through computer algorithm in its basic form. In order to successfully apply this as optimization method, Yang and Deb 41 used the following three approximate rules:
- (1)
Each cuckoo lays only one egg at a time, and dumps its egg in a randomly chosen nest;
- (2)
The best nests with high-quality eggs will be carried over to the next generations;
- (3)
The number of available host nests is fixed, and the egg laid by the host bird with a probability pa∈[0, 1]. In this case, the host bird can either throw the egg away or simply abandon the nest and build a completely new nest.
Based on these three rules, the basic steps of the CS are shown in Algorithm 1.
Begin |
Step 1: Initialization. Set the discovery rate (pa); initialize the population of n host nests randomly and each egg in a nest corresponding to a potential solution to the given problem; Set stopping criterion or the generation counter (G=1). |
Step 2: Generate new solutions x′ (but keep the current best), the procedure works as follows: |
for i=1 to d do |
xi′ = xi′ + α ⊕ Levy(λ) |
if (rand<pa) then |
xi′ = xi′+rand* (xr1 − xr2) |
endif |
end for |
where xi (i=1, 2,..., d) is the ith component of x′ and rand∼ U(0,1). |
Step 3: Keep best solutions; Rank the solutions and find the current best (xbest, f(xbest)) |
Step 4: Check the stopping criterion. If the stopping criterion (maximum number of iterations G) is satisfied, computation is terminated. Otherwise, step 2 is repeated. |
End. |
The cuckoo search algorithm
2.3. The global-best harmony search
Harmony search (HS) 43,68, as a relatively effective optimization technique, the optimization process is generally handled by three rules: memory consideration, pitch adjustment and random selection. The three key parameters which have a far-reaching effect on the performance of the HS are harmony memory consideration rate (HMCR), pitch adjustment rate (PAR), and distance bandwidth (bw). Additionally, the parameters also include harmony memory size (HMS), the number of improvisations (NI). In this paper, we employ GHS 48 as a mutation operation to ensure convergence of the CSGHS and enhance its ability of optimization effectively. The GHS is presented in Algorithm 2.
Begin |
Step 1: Initialize the HM. Set parameters HMS, HMCR, PAR, NI. |
Step2: Improvise a new harmony: the new harmony vector x′ = (x1′, x2′,..., x′d) is generated as follows: |
for i =1 to d do |
if (rand ≤ HMCR) then //memory consideration |
xi′ = xij, where j∼ U (1, ... , HMS). |
if rand ≤ PAR then //pitch adjustment |
xi′ = xibest, where best is the index of the best harmony |
end if |
else //random selection |
xi′ =LBi +r× (UBi − LBi), where r∼ U(0,1), rand∼ U(0,1) |
end if |
end for |
Step 3: Update harmony memory: if f (x′) < f (xworst), xworst = x′. (minimization objective) |
Update the best harmony vector. |
Step 4: Check the stopping criterion. If the stopping criterion is satisfied, computation is terminated. |
Otherwise, step 2 is repeated. |
End. |
The global-best harmony search algorithm
3. Hybrid CS with GHS for 0–1 KPs
In this section, we will propose a hybrid metaheuristic algorithm by integrating the global-best harmony search into the cuckoo search (CSGHS) for solving 0–1 knapsack problems. First, the hybrid encoding scheme and repair operator will be introduced. And then the proposed CSGHS will be described in detail. At last, the algorithm complexity is analyzed.
3.1. Encoding scheme
It is generally known that the 0–1 knapsack problem is a special integer linear programming problem. Additionally, from formula (1), we can infer that the feasible solution of 0–1 knapsack problem is n-dimension 0–1 vector. Hence, the individual was naturally represented by binary coding. Since the standard CS algorithm operates in continuous space, we cannot use it directly for solving optimization problems in binary space. So hybrid encoding scheme 55, 69 was used for solving 0–1 knapsack problem with CSGHS. The formal description is as follows. Let two-tuples<Xi, Yi> represent the ith cuckoo individual, where Xi = xi1, xi2,..., xid) ∈[−3.0, 3.0]d, and Yi = (yi1, yi2,..., yid) ∈{0,1}d. Sigmoid function is used to create a mapping between Xi and Yi. The conversion from d-dimensional real-valued vector to d-dimensional binary vector is as follows:
3.2. Repair operator
The 0–1 knapsack problem is also a constraint optimization problem. So constraint handling technique must be employed in order to handle the infeasible solution. Nowadays the more popular constraint handling technique is penalty function method and individual optimization method. In this paper, we adopt an effective greedy transform method (GTM) 55 to modify the infeasible solution as well as optimize the feasible solution.
3.3. The proposed approach: CSGHS
In this section, we will give a reasonable explanation for how and why we combine the GHS with CS to form an effective CSGHS, which not only improves the quality of the solutions, but also increases the diversity of the population, and then the efficiency of the algorithm is improved.
Generally, the main advantages of CS algorithm are the diversity of population strategy via randomization and search strategy by Lévy flights, there are still some aspects to be improved.
For CS, the search process relies too much on random, although Lévy flights is most suitable for the randomization on the global scale 41, the way of generating new solutions by random walk is less efficient than Lévy flights, so a rapid convergence rate cannot be guaranteed and at times it cannot avoid falling into local optimal. In addition, there lacks information exchange between the individuals, moreover, new solutions are not influenced by the best individual in the swarm. To address the shortcomings of the CS and make full use of the advantages of GHS, a new hybrid algorithm, called CSGHS, is proposed in which the GHS is embedded into the CS. By intuition, this improvement makes the new approach work efficiently on both continuous and discrete problems. The distinct difference between CSGHS and CS is that GHS as the mutation operator is applied to improve the original CS generating a new solution for each nest. In this manner, this new approach can generate diverse solutions with a view to exploring the search space on the global scale by Lévy flights of the CS, and concentrate on the search in a local region where the current optimum is most likely found by the mutation of the GHS.
Several improvements of CSGHS are described as follows:
The first improvement, and most important, is that the GHS completely replaces the random walk in CS in the stage of local search. As previously is mentioned, the GHS as a mutation operator was adopted in the CSGHS, with the aim of increasing diversity of the population and accelerating the convergence speed so as to enhance the performance.
The second improvement is to add mutation operator of DE/Best/1/Bin scheme into CSGHS, as was inspired by the mutation operator in DE algorithm. Its purpose is to further strengthen the effects of global optimal information on the new nests and the information exchange between individuals.
Based on the above analysis, concretely speaking, the evolution mechanism of the CSGHS performs in two stages. The first stage is to get a cuckoo i randomly (generate a solution) by Lévy flights and then evaluate its quality Fi. Cuckoo j is chosen randomly and then it will be replaced by cuckoo i only if Fi is superior Fj. The second stage we tune each element
With the above special design, the mainframe of the CSGHS for 0–1 knapsack problem is shown in Algorithm 3.
Begin |
Step 1: Sorting. According to value-to-weight ratio pi / wi (i = 1, 2, 3, ... , m) in descending order, a queue {s1, s2, ..., sm} of length m is formed. |
Step2: Initialization. Set the generation counter G=1; set the harmony memory consideration rate HMCR, the pitch adjustment rate PAR; Generate n cuckoo nests randomly {<X1, Y1>, <X2, Y2>, …, <Xn, Yn>}. |
Calculate the fitness for each individual, f (Yi), 1 ⩽ i ⩽ n, determine the global optimal individual <Xgbest, Ygbest>. |
Step 3: While the stopping criterion is not satisfied do |
for i=1 to n |
for j=1 to d |
xj′ = xj′ + α ⊕ Levy(λ) // Lévy flights |
if (rand<HMCR ) then //memory consideration |
xj′ = xji, where i ∼ U (1, n). |
if rand<PAR then //pitch adjustment |
xj′ = xjbest |
else |
xj′ = xjbest+F×(xjq − xjr ), where q∼U (1, n), r∼ U (1, n) |
end if |
else //random selection |
xj′ =LBj + r×(UBj −LBj ), where r∼ U(0,1 ) |
end if |
end for |
Perform GTM method to repair and optimize the individuals |
end for |
Keep best solutions. |
Rank the solutions in descending order and find the current best (Ybest, f (Ybest)). |
G=G+1 |
Step 4: End while |
End. |
The mainframe of the CSGHS algorithm for 0–1 knapsack problem
3.4. Algorithm complexity
CSGHS is composed of three stages: the sorting by value-to-weight ratio, the initialization and the iterative search. The quick sorting has time complexity O(n log(n)). The generation of the initial cuckoo nests has time complexity O(n×d). The iterative search consists of four steps (comment statements in Algorithm 3), i.e. the Levy flights, memory consideration, pitch adjustment, and random selection which costs the same time O(n×d). Further, the major time cost of GTM is the quick sort which has calculated at the start of this section. In summary, the overall complexity of the proposed CSGHS is O(n log (n))+O(n×d)+O(n×d)= O(n log(n))+O(n×d). It does not change compared with the original CS algorithm.
4. Simulation Experiments
4.1. Experimental data set
Since the difficulty of knapsack problems is greatly affected by the correlation between profits and weights 66, 71, six groups of 0–1 KP instances randomly generated are presented in Table 1. The correlation of six types of instances is shown in Fig. 1. Here we use the function Rand (a, b) to represent an integer uniformly distributed in [a, b]. Each group contains six 0–1 KP instances and the dimension is 300, 500, 800, 1000, 1200, and 1500. These thirty-six instances are marked as KP1, KP2, … , KP36, respectively.
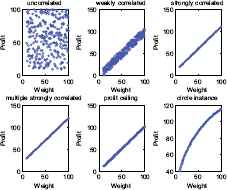
Six classes of instances with 300 items
| Correlation | wi | pi |
|---|---|---|
| Uncorrelated instance | Rand(10,100) | Rand(10,100) |
| Weakly correlated instance | Rand(10,100) | Rand(wi − 10, wi + 10 ) |
| Strongly correlated instance | Rand(10,100) | wi + 10 |
| Multiple strongly correlated instance | Rand(10,100) | wj +30, if mod(wj,6
)=0 wj + 20, else |
| Profit ceiling instance | Rand(10,100) | 3× ⌈wj / 3⌉ |
| Circle instance | Rand(10,100) |
where d=2/3, R=10. For each data set we set the value of the capacity
Six groups of 0–1 KP instances
4.2. Experimental setup and parameters setting
To better understand the CSGHS, we compared its performance on 36 knapsack problems (KP1–KP36) with three other optimization approaches, which are DE, SFLA and CS. DE 72 is a vector-based evolutionary algorithm with self-organizing tendency and does not use the information of derivatives. SFLA is a meta-heuristic optimization method that imitates the memetic evolution of a group of frogs while casting about for the location that has the maximum amount of available food 73.
In our experiments, we set the parameters as follows. The proposed CSGHS includes four key parameters: the population size P=40, the harmony memory consideration rate HMCR=0.9, the pitch adjustment rate PAR=0.3 and amplification factor F=0.3. For DE, the population size P=40, crossover probability Cr=0.9, amplification factor F=0.3, basic DE/Rand/1/Bin scheme. For SFLA, the population size P=40, which is partitioned into M =4 memeplexes, each containing N=10 frogs (i.e. P=M×N).
In order to make a fair comparison, all computational experiments are conducted with Visual C++ 6.0. The test environment is set up on a PC with AMD Athlon(tm) II X2 250 Processor 3.01 GHz, 1.75G RAM, running on Windows 7. The experiment on each instance was repeated 30 times independently. Further, best solution, worst solution, mean, median, standard deviation (STD) for all the solutions are given in related tables. In addition, the maximum run-time was set to 5 seconds for 300-dimensional and 500-dimensional instances, 8 seconds for 800-dimensional, 1000-dimensional, and 1200-dimensional instances and 10 seconds for 1500-dimensional instances.
4.3. Numerical optimization
In order to make an overall investigation about the performance of CSGHS, a number of simulation and experiment research have been carried out. Six classes of 0–1 knapsack problems with large scales listed in Table 1. The number of items is set to 300, 500, 800, 1000, 1200, and 1500, respectively. The experimental results are reported in Tables 2–7. The best values are emphasized in boldface. In addition, comparisons of the best profits obtained from the CSGHS with those obtained from DE, SFLA and CS for six KP instances with 1500 items among 30 independent runs are shown in Figs 2–7, respectively. Specifically, the convergence curves of four algorithms on 1500 items are also graphically illustrated in Figs 8–13, respectively.
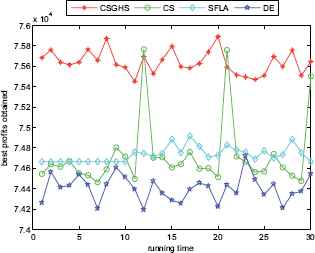
The best profits obtained in 30 runs for KP6
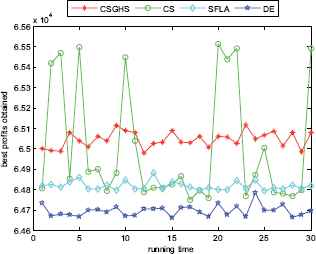
The best profits obtained in 30 runs for KP12
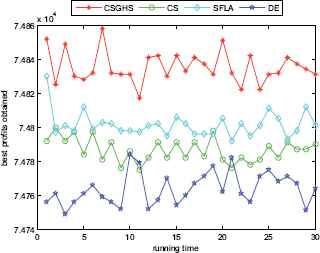
The best profits obtained in 30 runs for KP18
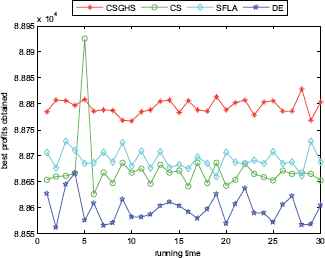
The best profits obtained in 30 runs for KP24
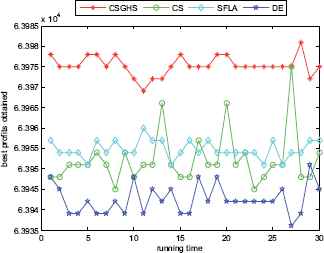
The best profits obtained in 30 runs for KP30
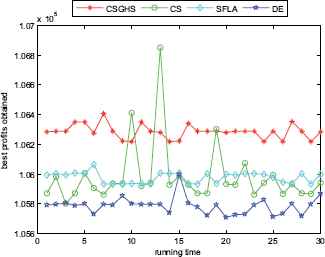
The best profits obtained in 30 runs for KP36
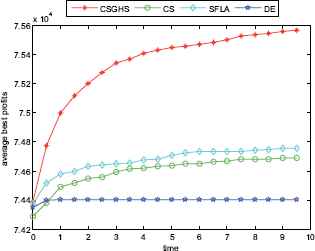
The convergence graphs of KP6
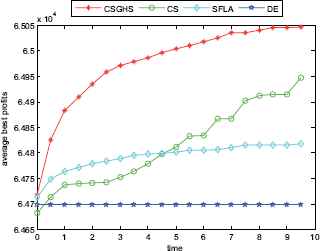
The convergence graphs of KP12
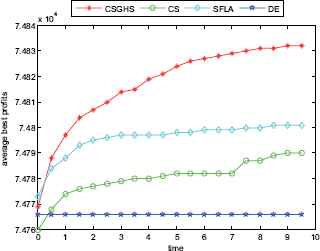
The convergence graphs of KP18
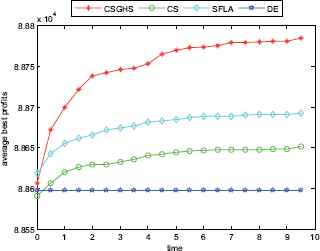
The convergence graphs of KP24
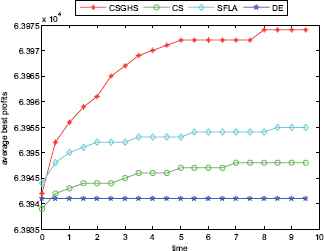
The convergence graphs of KP30
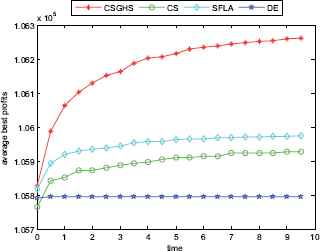
The convergence graphs of KP36
| Instance | Algorithm | Best | Worst | Mean | Median | STD |
|---|---|---|---|---|---|---|
| KP1 | SFLA | 15202 | 15095 | 15145 | 15141 | 23.45 |
| DE | 15334 | 15088 | 15287 | 15301 | 54.45 | |
| CS | 15224 | 15024 | 15092 | 15081 | 51.37 | |
| CSGHS | 15338 | 15281 | 15304 | 15304 | 12.26 | |
| KP2 | SFLA | 26065 | 25915 | 25968 | 25956 | 32.92 |
| DE | 26333 | 25751 | 26099 | 26096 | 135.88 | |
| CS | 26208 | 25786 | 25936 | 25911 | 103.4 | |
| CSGHS | 26387 | 26230 | 26329 | 26337 | 34.00 | |
| KP3 | SFLA | 39753 | 39563 | 39647 | 39642 | 54.87 |
| DE | 39652 | 39215 | 39410 | 39399 | 113.28 | |
| CS | 40223 | 39416 | 39565 | 39514 | 179.98 | |
| CSGHS | 40342 | 40056 | 40182 | 40190 | 68.87 | |
| KP4 | SFLA | 49369 | 49185 | 49248 | 49240 | 46.98 |
| DE | 49246 | 48835 | 48989 | 48979 | 101.11 | |
| CS | 49767 | 49024 | 49164 | 49142 | 143.08 | |
| CSGHS | 50027 | 49717 | 49846 | 49835 | 84.36 | |
| KP5 | SFLA | 60225 | 59936 | 60047 | 60049 | 62.89 |
| DE | 59932 | 59488 | 59707 | 59727 | 110.39 | |
| CS | 60629 | 59708 | 59939 | 59884 | 166.43 | |
| CSGHS | 60951 | 60616 | 60788 | 60791 | 79.79 | |
| KP6 | SFLA | 74915 | 74662 | 74731 | 74721 | 74.09 |
| DE | 74719 | 74189 | 74404 | 74418 | 126.44 | |
| CS | 75762 | 74461 | 74720 | 74610 | 336.75 | |
| CSGHS | 75889 | 75452 | 75639 | 75631 | 112.26 |
Experimental results of four algorithms with uncorrelated KP instances
From the results of Tables 2, 4–7, we can plainly perceive that CSGHS achieves decisive advantage in performance over the other three algorithms and it obtains the best results on all the instances, as can be seen from the third column to the sixth column of Tables 2, 4–7. On closer inspection, the SFLA gains the smallest STD values on more than two-thirds cases. For the other ten cases, similar numerical stabilities are observable in CS and CSGHS. With regard to DE, it may not be adept in solving 0–1 KPs as its overall performance is obviously inferior to that of the other three algorithms.
| Instance | Algorithm | Best | Worst | Mean | Median | STD |
|---|---|---|---|---|---|---|
| KP13 | SFLA | 14807 | 14797 | 14799 | 14797 | 3.48 |
| DE | 14797 | 14781 | 14789 | 14787 | 4.90 | |
| CS | 14804 | 14791 | 14797 | 14797 | 2.43 | |
| CSGHS | 14807 | 14797 | 14804 | 14807 | 4.44 | |
| KP14 | SFLA | 25519 | 25507 | 25514 | 25514 | 2.40 |
| DE | 25502 | 25481 | 25492 | 25493 | 4.21 | |
| CS | 25514 | 25502 | 25506 | 25505 | 3.49 | |
| CSGHS | 25533 | 25515 | 25523 | 25525 | 4.97 | |
| KP15 | SFLA | 40124 | 40107 | 40113 | 40114 | 4.40 |
| DE | 40111 | 40068 | 40089 | 40088 | 8.66 | |
| CS | 40107 | 40096 | 40103 | 40105 | 3.88 | |
| CSGHS | 40147 | 40126 | 40132 | 40130 | 5.54 | |
| KP16 | SFLA | 49383 | 49363 | 49374 | 49373 | 5.20 |
| DE | 49363 | 49333 | 49346 | 49345 | 7.50 | |
| CS | 49380 | 49350 | 49364 | 49363 | 7.04 | |
| CSGHS | 49403 | 49383 | 49393 | 49393 | 6.52 | |
| KP17 | SFLA | 60566 | 60541 | 60551 | 60550 | 5.22 |
| DE | 60540 | 60501 | 60519 | 60519 | 8.55 | |
| CS | 60558 | 60530 | 60542 | 60540 | 6.77 | |
| CSGHS | 60587 | 60567 | 60573 | 60570 | 5.32 | |
| KP18 | SFLA | 74830 | 74792 | 74801 | 74801 | 7.44 |
| DE | 74784 | 74749 | 74764 | 74761 | 9.50 | |
| CS | 74800 | 74775 | 74787 | 74786 | 6.83 | |
| CSGHS | 74858 | 74817 | 74835 | 74832 | 9.31 |
Experimental results of four algorithms with strongly correlated KP instances
| Instance | Algorithm | Best | Worst | Mean | Median | STD |
|---|---|---|---|---|---|---|
| KP19 | SFLA | 18388 | 18368 | 18377 | 18379 | 7.91 |
| DE | 18387 | 18335 | 18354 | 18348 | 15.25 | |
| CS | 18386 | 18355 | 18368 | 18368 | 4.73 | |
| CSGHS | 18388 | 18388 | 18388 | 18388 | 0.00 | |
| KP20 | SFLA | 29589 | 29560 | 29567 | 29568 | 5.79 |
| DE | 29548 | 29488 | 29519 | 29520 | 14.10 | |
| CS | 29589 | 29527 | 29555 | 29549 | 13.94 | |
| CSGHS | 29627 | 29589 | 29605 | 29609 | 9.81 | |
| KP21 | SFLA | 47737 | 47695 | 47713 | 47715 | 10.54 |
| DE | 47704 | 47620 | 47659 | 47657 | 20.68 | |
| CS | 47727 | 47673 | 47696 | 47695 | 15.09 | |
| CSGHS | 47797 | 47757 | 47776 | 47777 | 10.09 | |
| KP22 | SFLA | 60612 | 60575 | 60590 | 60590 | 8.22 |
| DE | 60572 | 60508 | 60534 | 60530 | 13.98 | |
| CS | 60607 | 60540 | 60576 | 60574 | 16.96 | |
| CSGHS | 60672 | 60630 | 60656 | 60652 | 14.94 | |
| KP23 | SFLA | 72122 | 72072 | 72089 | 72088 | 11.88 |
| DE | 72072 | 71973 | 72018 | 72018 | 19.38 | |
| CS | 72094 | 72031 | 72058 | 72057 | 15.93 | |
| CSGHS | 72212 | 72145 | 72166 | 72167 | 16.17 | |
| KP24 | SFLA | 88728 | 88660 | 88692 | 88688 | 17.59 |
| DE | 88666 | 88562 | 88598 | 88595 | 25.88 | |
| CS | 88687 | 88626 | 88663 | 88665 | 14.88 | |
| CSGHS | 88828 | 88767 | 88794 | 88788 | 14.54 |
Experimental results of four algorithms with multiple strongly correlated KP instances
| Instance | Algorithm | Best | Worst | Mean | Median | STD |
|---|---|---|---|---|---|---|
| KP25 | SFLA | 12957 | 12957 | 12957 | 12957 | 0.00 |
| DE | 12957 | 12951 | 12953 | 12954 | 1.83 | |
| CS | 12957 | 12954 | 12957 | 12957 | 0.76 | |
| CSGHS | 12957 | 12957 | 12957 | 12957 | 0.00 | |
| KP26 | SFLA | 20307 | 20301 | 20302 | 20301 | 1.67 |
| DE | 20301 | 20292 | 20294 | 20294 | 2.17 | |
| CS | 20304 | 20295 | 20299 | 20298 | 1.86 | |
| CSGHS | 20307 | 20307 | 20307 | 20307 | 0.00 | |
| KP27 | SFLA | 32814 | 32802 | 32806 | 32805 | 2.13 |
| DE | 32802 | 32793 | 32797 | 32796 | 2.63 | |
| CS | 32811 | 32799 | 32803 | 32802 | 3.12 | |
| CSGHS | 32826 | 32814 | 32820 | 32820 | 2.65 | |
| KP28 | SFLA | 43263 | 43257 | 43259 | 43260 | 2.01 |
| DE | 43257 | 43245 | 43249 | 43248 | 3.57 | |
| CS | 43269 | 43251 | 43257 | 43254 | 4.41 | |
| CSGHS | 43284 | 43269 | 43274 | 43275 | 3.12 | |
| KP29 | SFLA | 51396 | 51384 | 51389 | 51390 | 2.48 |
| DE | 51384 | 51372 | 51378 | 51378 | 3.04 | |
| CS | 51399 | 51378 | 51385 | 51384 | 4.32 | |
| CSGHS | 51414 | 51399 | 51407 | 51405 | 4.29 | |
| KP30 | SFLA | 63960 | 63951 | 63955 | 63954 | 2.22 |
| DE | 63951 | 63936 | 63942 | 63942 | 3.62 | |
| CS | 63975 | 63945 | 63953 | 63951 | 6.43 | |
| CSGHS | 63981 | 63969 | 63975 | 63975 | 2.41 |
Experimental results of four algorithms with profit ceiling KP instances
| Instance | Algorithm | Best | Worst | Mean | Median | STD |
|---|---|---|---|---|---|---|
| KP31 | SFLA | 21330 | 21262 | 21263 | 21278 | 25.74 |
| DE | 21333 | 21192 | 21264 | 21277 | 32.46 | |
| CS | 21333 | 21194 | 21261 | 21261 | 18.57 | |
| CSGHS | 21335 | 21265 | 21333 | 21329 | 12.48 | |
| KP32 | SFLA | 35348 | 35341 | 35344 | 35345 | 1.70 |
| DE | 35343 | 35184 | 35247 | 35267 | 38.08 | |
| CS | 35345 | 35271 | 35297 | 35277 | 31.29 | |
| CSGHS | 35419 | 35347 | 35416 | 35403 | 26.04 | |
| KP33 | SFLA | 56136 | 56063 | 56129 | 56113 | 29.56 |
| DE | 56063 | 55914 | 55964 | 55954 | 44.95 | |
| CS | 56280 | 55988 | 56057 | 56061 | 55.01 | |
| CSGHS | 56346 | 56205 | 56276 | 56278 | 35.37 | |
| KP34 | SFLA | 70876 | 70798 | 70831 | 70834 | 33.98 |
| DE | 70806 | 70641 | 70696 | 70684 | 38.21 | |
| CS | 70915 | 70729 | 70789 | 70797 | 42.50 | |
| CSGHS | 71085 | 70949 | 71014 | 71030 | 34.97 | |
| KP35 | SFLA | 84173 | 84038 | 84096 | 84080 | 39.95 |
| DE | 84040 | 83820 | 83912 | 83899 | 56.64 | |
| CS | 84645 | 83954 | 84055 | 84033 | 121.94 | |
| CSGHS | 84396 | 84187 | 84319 | 84297 | 54.62 | |
| KP36 | SFLA | 106066 | 105931 | 105993 | 105977 | 36.39 |
| DE | 106000 | 105706 | 105793 | 105790 | 57.59 | |
| CS | 106853 | 105799 | 105929 | 106006 | 206.71 | |
| CSGHS | 106407 | 106217 | 106288 | 106287 | 48.04 |
Experimental results of four algorithms with circle KP instances
Table 3 summarizes the experimental results obtained by the four methods to the weakly-correlated instances. From Table 3 we can infer that the performance of CSGHS, CS, SFLA and DE are comparable. DE obtained the best, mean, median results for KP7, KP8 and CS attained the best results for the last four cases. SFLA still showed the best stability among four methods. Although the optimal solutions obtained by the CSGHS are poorer than DE or CS, the CSGHS gets the worst, mean, median results on KP9–KP12. Unfortunately, although weakly correlated knapsack problem are closer to the real world situations 66, the CSGHS does not appear overwhelming superior to the other three algorithms in solving such knapsack problems.
| Instance | Algorithm | Best | Worst | Mean | Median | STD |
|---|---|---|---|---|---|---|
| KP7 | SFLA | 13110 | 13089 | 13098 | 13099 | 6.22 |
| DE | 13202 | 13158 | 13186 | 13186 | 9.76 | |
| CS | 13157 | 13069 | 13094 | 13087 | 21.91 | |
| CSGHS | 13178 | 13154 | 13169 | 13169 | 6.59 | |
| KP8 | SFLA | 21760 | 21702 | 21722 | 21717 | 15.82 |
| DE | 21951 | 21745 | 21858 | 21859 | 37.61 | |
| CS | 21935 | 21670 | 21746 | 21722 | 76.53 | |
| CSGHS | 21871 | 21803 | 21832 | 21830 | 12.43 | |
| KP9 | SFLA | 34704 | 34651 | 34673 | 34674.5 | 12.55 |
| DE | 34814 | 34578 | 34721 | 34718 | 64.50 | |
| CS | 34987 | 34621 | 34697 | 34654 | 100.38 | |
| CSGHS | 34850 | 34795 | 34824 | 34825 | 14.00 | |
| KP10 | SFLA | 43305 | 43258 | 43277 | 43276 | 12.63 |
| DE | 43327 | 43162 | 43217 | 43211 | 43.64 | |
| CS | 43737 | 43216 | 43340 | 43264 | 166.53 | |
| CSGHS | 43484 | 43386 | 43440 | 43442 | 22.39 | |
| KP11 | SFLA | 51989 | 51797 | 51890 | 51875 | 58.65 |
| DE | 51947 | 51444 | 51600 | 51569 | 108.83 | |
| CS | 53333 | 51601 | 51831 | 51788 | 299.35 | |
| CSGHS | 52711 | 52354 | 52556 | 52565 | 76.89 | |
| KP12 | SFLA | 64880 | 64792 | 64818 | 64812 | 21.31 |
| DE | 64783 | 64661 | 64696 | 64697 | 27.06 | |
| CS | 65515 | 64750 | 65004 | 64860 | 294.16 | |
| CSGHS | 65116 | 64980 | 65045 | 65044 | 38.14 |
Experimental results of four algorithms with weakly correlated KP instances
Figs. 2–7 show a comparison of the best profits obtained by applying the four algorithms for six classes of problems with 1500-dimensional functions in 30 runs. The search space of the 1500-dimensional functions is expanded dramatically to 21500, which is a challenge for CSGHS, CS, SFLA and DE. Thus, DE failed to come at any global optima of all the six high-dimensional functions, while the results of SFLA fluctuated around certain value, as we had expected. Additionally, the CS can get the optimal solution occasionally, which shows it has poorer stabilization and is consistent with the STD value above. The CSGHS wins obvious advantages. As mentioned above, weakly correlated problem instances are difficult to solve in the case of CSGHS.
To investigate further the performance of the four approaches, the average convergence curves of CSGHS, CS, SFLA and DE are drawn in Figs. 8–13. The optimization of the small-size problems is simple. However, when the dimensionality is increased, the CSGHS takes the lead obviously and outperforms the other three methods. From Figs. 8–13, it is observed that CSGHS have a quick convergence speed, as is benefited from the GHS. SFLA performs the second best in hitting the optimum. DE shows premature phenomenon in the evolution and does not offer satisfactory performance.
5. Conclusions
In this paper, a hybrid cuckoo search algorithm with global-best harmony search (CSGHS) was proposed to solve 0–1 KP efficiently and effectively. To address the shortcomings of the CS, the GHS as a mutation operator was adopted in the CSGHS to strengthen the search ability. Another effective mutation operator of DE/Best/1/Bin scheme in DE is embedded into CSGHS to increase the diversity of population. Finally, CSGHS was tested on different correlated knapsack problem instances with low-dimensional and high-dimensional. The experiments reveal that the proposed approach greatly outperforms CS, SFLA and DE with regard to the solution accuracy and the convergence speed, particularly on tackling the large-size intractable 0–1KPs, which shows that the proposed CSGHS is an effective optimization tool.
The future work is to consider and solve other knapsack problem, such as multi-scenario max-min knapsack problem, bi-level 0–1 knapsack problem, Multidimensional Knapsack Problem.
Secondly, in the future, more engineering optimization problems will be used to further verify our proposed method, such as flowshop scheduling problems (FSP) 74–75, image processing 76–77, video coding 78, and wireless sensor networks 79.
Thirdly, our proposed method will surely work well in combination with other computational intelligence algorithms, such as minimax probability machine 79, support vector classification 81, fuzzy C-means 82, and least significant bit (LSB) matching 83–84.
Acknowledgment
This work was supported by Hebei GEO University Youth Foundation (No. QN201601), Natural Science Foundation of Jiangsu Province (No. BK20150239) and National Natural Science Foundation of China (No. 61503165).
Footnotes
References
Cite this article
TY - JOUR AU - Yanhong Feng AU - Gai-Ge Wang AU - Xiao-Zhi Gao PY - 2016 DA - 2016/12/01 TI - A Novel Hybrid Cuckoo Search Algorithm with Global Harmony Search for 0–1 Knapsack Problems JO - International Journal of Computational Intelligence Systems SP - 1174 EP - 1190 VL - 9 IS - 6 SN - 1875-6883 UR - https://doi.org/10.1080/18756891.2016.1256577 DO - 10.1080/18756891.2016.1256577 ID - Feng2016 ER -
