Evaluation of Knowledge Management Tools by Using An Interval Type-2 Fuzzy TOPSIS Method
- DOI
- 10.1080/18756891.2016.1237182How to use a DOI?
- Keywords
- Interval Type-2 fuzzy sets; Fuzzy multiple attributes group decision making; TOPSIS; KM tools selection
- Abstract
Knowledge management (KM) systems can provide businesses a wide range of advantages and efficiency improvements. Increasing competition forces companies to seek new ways to streamline their processes and manage their information and knowledge better, leading to increased demand for KM solutions. Considering various needs of organizations and diverse features of available KM alternatives, choosing the most suitable KM tool is an important decision for businesses. The contribution of this paper to the KM literature is a KM evaluation framework for decision makers to compare available KM products of different vendors by first identifying relevant evaluation criteria and then proposing a group decision making framework using the Interval Type-2 TOPSIS technique. This method has more flexibility in handling uncertainties compared to the Type-1 fuzzy sets and enables decision makers to effectively analyze, compare and select the most appropriate KM tools. The framework is also used in a case study for the sake of demonstrating its potential in businesses.
- Copyright
- © 2016. the authors. Co-published by Atlantis Press and Taylor & Francis
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Successful knowledge management (KM) can support businesses in obtaining sustainable competitive advantage for businesses1,2,3,4,5. This raises interest of industry managers and academicians. KM tools are information technology (IT) based systems which support and improve those processes that aim to create, store, retrieve, transfer and apply knowledge6. These tools do not only enable businesses to transfer knowledge to its departments, but also integrate many knowledge processes for solving business problems as an organizational information system7,8. Furthermore, KM tools promote and facilitate knowledge processes in decision-making and can be used as enablers in supply chain management for connecting an enterprise with its customers and suppliers9,10,11.
There exist various KM software that have specific functionalities that suit different needs of organizations, requiring companies to reach a decision in selecting the most appropriate software solution among many in the market. Taking the significant amounts of financial investment as well as the potential risks and benefits into account, selection of a suitable KM tool represents an important corporate decision12. On the other hand, there are many KM system alternatives and each alternative can affect different stakeholders within a company. Considering the overall complexity of business activities and resource limitations, finding the most suitable KM tool is a difficult and time intensive task. Because of these challenges, the selection of a suitable KM is a decision making problem that is not fully defined yet.
When selecting the most suitable KM software, there are many criteria to consider and different decision makers (DMs) to consult. This adds up to the complexity of the solution process and necessitates a sound, systematic approach for critically assessing available KM tool alternatives and identifying the most suitable one. The aim is not only to choose the best alternative among many, but also to decrease the time and effort used for taking the decision and for building consensus among DMs. Addressing this research gap12,13,14,15,16, this article proposes an assessment framework that can provide a way to effectively evaluate the available KM tool alternatives.
There are many different factors that can come into question when selecting one tool from many different alternatives. Therefore, a multi criteria analysis and solution approach can be followed for this KM tool evaluation problem. There are many useful multi criteria decision making (MCDM) methods available to decision makers, with their advantages and drawbacks. This paper uses a decision framework which makes use of the Interval Type-2 fuzzy TOPSIS method. As expert opinions constitute a significant and integral component of this process, fuzzy data will need to be evaluated. To deal with uncertainty in alternative selection and to overcome the vagueness limitations of MCDM methods, various authors utilized fuzzy sets17. Ordinary fuzzy sets (type-1)18 can cover uncertainties of linguistic words to some extent. However, Interval Type-2 fuzzy sets19 are preferable for gaining more degrees of freedom for handling the unavoidable fuzziness and uncertainty of real world conditions20,21.
During this study, the focus is about the analysis of KM tools using a fuzzy framework. The study differs from the literature of KM tools as it uses a MCDM technique with Interval Type-2 fuzzy sets. Therefore, the analysis can better handle the uncertainty and encompass the fuzzy decision in the case of KM. Even if similar management tools are studied with Type-1 fuzzy sets, there is no study about the selection of KM tools by applying Interval Type-2 fuzzy sets. In order to highlight the robustness of our framework, the selection problem is also resolved with the Type-1 fuzzy sets and crisp approach. The motivation of our analysis is guided by the literature review where the selection problem of KM tools represent high uncertainty and critical availability. Furthermore, our analysis denotes a quantitative contribution to the KM problem by indicating how this problem might be dealt with high uncertainty to select the appropriate software environment.
The article is structured in the following order; Section 2 introduces the proposed valuation framework and right after that in Section 3 algebraic operations of Interval Type-2 fuzzy sets and their ranking are given. Section 4 presents the computational steps of the proposed methodology using the method called Interval Type-2 fuzzy TOPSIS. Following that, Section 5 applies the framework on a KM tool selection case for a private company in Turkey. As the final part, Section 6 discusses the results and provides the concluding remarks.
2. KM tools evaluation framework
2.1. Literature Survey of KM tools evaluation
KM tools in the software market have different features, parallel to improvements in IT and multiple, changing needs in numerous industries and sometimes conflicting objectives. From a business perspective, the proliferation of a high number of software systems furthermore complicates the decision making procedure. Influencing factors complicating the tasks of DMs can be summarized as below:
- •
Users with insufficient experience.
- •
Continuous advancement and improvements in IT.
- •
Abundance of different commercial KM software products.
- •
Possible hardware-software compatibility problems.
- •
Functional disparities among software packages.
In related literature about KM tool selection, Ngai and Chan12 made use of a model based on Analytic Hierarchy Process (AHP)27 to support decision makers in evaluating different alternatives of KM products and applied the framework on a case study, underlining that their primary focus was the framework they proposed. Considering that the selection of an appropriate KM tool inevitably involves subjective evaluation, Liu and Peng13 used a fuzzy AHP model in their paper. Büyüközkan and Feyzioğlu28 applied a Choquet integral based aggregation methodology to rate KM systems of different vendors. In another article, Yu14 established an evaluation system that combined a qualitative index with a quantitative index based on the features of the KM system of the enterprise, and constructed an extended evaluation based matter-element model of the system. Büyüközkan et al.15 presented a fuzzy VIKOR method which used fuzzy logic as well as group decision making approaches to handle the vagueness and granularity of linguistic expressions. In order to support the evaluation and selection of KM systems from the users perspective, Li et al16, recently used an MCDM approach which combines quality function deployment (QFD) with TOPSIS in intuitionistic fuzzy environment.
Until recently, Type-1 fuzzy logic was used more frequently in research papers. However, related literature is witnessing a surge in the use of Type-2 fuzzy logic29. Type-1 fuzzy set is based on the assumption of certainty in the membership function definitions. On the other hand, the membership functions of Type-2 fuzzy sets have 3 dimensions and do take uncertainty into account. This added third dimension and the footprint of uncertainty are two novelties of Type-2 fuzzy sets which represent new degrees of freedom, enabling direct modeling and handling uncertainties. Considering that human decisions and expressions involve uncertainty, type-2 fuzzy sets present a more suitable approach for handling the subjectivity and the membership imprecision of model. Therefore, this paper uses a decision framework that is based on the technique of Interval Type-2 fuzzy TOPSIS. This is original because there is no other research combining the Interval Type-2 fuzzy and TOPSIS methods for evaluating software alternatives or KM tool selection problems.
2.2. KM tools evaluation criteria
The evaluation criteria are determined based on various information sources, including product briefings, software demos, vendor surveys and a careful literature study12,16,28,30,31,33,34,35. In order to ensure that the identified criteria are sufficiently well formulated and properly understood, the topic is discussed with DMs and the criteria are validated by external professional experts (KM consultants and vendors themselves). The following criteria are determined for the KM tool evaluation:
- •
Software enhancement possibilities (C1): KM tools are an integral part of other applications used in IT systems of a company. Therefore, interface with exchange servers, project reports, Enterprise Resource Planning and finance systems or their relevant parameters need to be flexible enough. A KM tool should be able to allow new functions that are developed from scratch and provide a platform where additional development can easily be made.
- •
Compliance with company standards (C2): In a global company working in several geographic locations, a wide range of products are needed. Isolated, local solutions can lead to complexities and even disorders in terms of application integration and reporting, leading to time consumption, inefficiency and additional cost. Standardization of IT applications can provide benefits in this respect, where the software complies with the standards of the company.
- •
Document management (C3): Knowledge organizations embed big volumes of data into documents, which can increase productivity if documents are managed effectively. Proper document management systems need to include features like exhaustive authorization options, alerts, handy searching mechanisms, discussions and versioning for documents, beside others.
- •
Collaboration (C4): Collaboration is one of the fundamental evaluation criteria of KM tools, as it can leverage implicit knowledge. Teamwork, communication within teams, and collaborative solutions produce a considerable proportion of knowledge assets. Furthermore, collaboration is an important component for an e-business (the other two components being information and commerce).
- •
Portal functions (C5): Portals are user-friendly entry points into the corporate knowledge domain of a company. Portals are expected to be user friendly and customizable for users, and are expected to have the capability for using several carefully selected applications with a single sign-in.
- •
Workflow facilities (C6): In a business, workflow management connects management of documents with the management of processes, where work-flow facilities are expected to hasten the flow of documents through the internal processes. The path a document travels within a company is defined and responsibilities and actions on the document are described, such as rejection and approval functions and the person in charge of that function.
- •
User Friendliness (C7): Integration of KM products can have change management dimensions in an organization. A KM system that is not user friendly can delay its adoption, lead to internal resistance and ultimately to inefficiency. Such difficulties may even prevent project teams from successfully implement the KM system, causing additional challenges. Clearly, a user friendly KM system will be more easily accepted within an organizations across departments.
- •
Purchasing costs (C8): Similar to many other decision making problems, purchase decisions are largely affected by the up-front costs such as KM software purchasing, setting up and training.
- •
Operating costs (C9): Operating costs are defined as running costs needed for continuing everyday operations of a KM tool.
- •
Vendor performance (C10): Vendors are business partners who are expected to ensure a certain level of service quality and support provided to customers. Vendors with sufficient expertise and experience with the KM will give customers more confidence. The stability of the vendor is another important dimension, where its financial status, scale and local support level should not be neglected.
3. The Ranking Values and the Arithmetic Operations of Interval Type-2 Fuzzy Sets
The definitions and operations on Type-2 fuzzy sets has to be given in order to be more luminous about the trapezoidal Interval Type-2 fuzzy numbers . The definitions in the study of Chen and Lee24 are taken in this study for their clarity. Moreover, the ranking method derived from the article of Wu and Mendel36 is used in the proposed study because of its appropriateness and accuracy.
Let à be a Type-1 trapezoidal fuzzy set, à = (a1,a2,a3,a4;H1(Ã),H2(Ã)), where H1(Ã) states the membership value of the element a2; H2(Ã) states the membership value of the element a3; 0 ⩽ H1(Ã) ⩽ 1 and 0 ⩽ H2(Ã) ⩽ 1. As Mendel et al.20 defined; a Type-2 fuzzy set
Let
3.1. Arithmetic operations on trapezoidal Interval Type-2 fuzzy sets
The arithmetic operations that are quoted from Lee and Chen37 between trapezoidal Interval Type-2 fuzzy sets will be reviewed in this subsection. Let us assume two trapezoidal Interval Type-2 fuzzy sets as follows:
3.2. Ranking of trapezoidal Interval Type-2 fuzzy sets
A centroid based ranking method developed by Wu and Mendel36 will be used as a ranking operation in this study. Unlike the work of Chen and Lee24, this method is preferred because it is more efficient and easy to understand. The ranking method can be viewed as a generalization of Yager’s first ranking method for Type-1 fuzzy sets38 to Interval Type-2 fuzzy sets.
The centroid C(Ã) of an Interval Type-2 fuzzy set
Centroid-based ranking method: First compute the average centroid for each Interval Type-2 fuzzy set
4. Interval Type-2 Fuzzy TOPSIS Method in a Group Decision Making Setting
4.1. Literature survey of Type-2 Methods
A technique that is often applied in MCDM is ”Technique for Order Preference by Similarity to Ideal Solution” (TOPSIS)22. It is an efficient methodology that is able to provide decision makers with an indisputable preference order23. The hybrid decision making framework proposed in this article has the benefit of making use of the advantages of both TOPSIS and Type-2 fuzzy set methods24. Recently, Chatterjee and Kar25 combined these methods to evaluate the risky nature of six financial institutions of supply chain management. Moreover, Celik et al.26 made use of these methods to assess and improve passenger satisfaction in the systems of public transportation. Interval Type-2 fuzzy TOPSIS method is first familiarized by Chen and Lee24. Our study utilizes a modified version of this Interval Type-2 TOPSIS method.
Although it is a hot topic, there are relatively few studies. The service quality of public transportation systems in Istanbul are discussed with the opinions of the passengers by Celik et al.26. They assessed the satisfaction levels of passengers of Istanbul’s public transportation system first with a questionnaire and then with statistical methods. For these purposes, the Interval Type-2 fuzzy technique has been used in conjuction with TOPSIS and GRA methods. In another paper, Cebi and Otay39 introduced the application of fuzzy TOPSIS method with Interval Type-2 fuzzy sets on a facility location selection problem for a cement factory. Chen et al.41 extended the QUALIFLEX method for dealing with MCDM problems in an Interval Type-2 environment. The quoted study explicated the convenience and practicability of the presented techniques for a medical (acute inflammatory demyelinating disease) MCDM problem. The validity of the proposed model is then verified with the help of a comparative analysis using another outranking technique. Celik et al.42 discussed the improvement of satisfaction levels in the municipal rail transit network of Istanbul city. In their article, the authors evaluated customer satisfaction level with VIKOR method. Another interesting study43 integrated the techniques of GRA, interval-valued fuzzy sets and VIKOR for the sake of evaluating the service quality of a Chinese cross-strait airlines company, with the help of passenger questionnaires.
A Type-2 fuzzy sets extended fuzzy analytic hierarchy process was developed by Kahraman et al.44. They applied their advanced model to a supplier selection problem. Ghorabaee et al.45 offered another multi criteria model with Interval Type-2 sets integrated fuzzy COPRAS method in the selection process of suppliers. An extension of MULTI-MOORA method, another MCDM technique by Interval Type-2 fuzzy sets was provided by Baležentis and Zeng46 for a personnel selection problem. Chen47 developed an extension of ELECTRE method with Type-2 fuzzy sets and presented the signed distance-based hybrid averaging operation for forming the collective decision matrix. The author applied the presented method to a worked out supplier selection problem. In another paper, Chen40 again used the Interval Type-2 fuzzy set technique, which is less precise and more ambiguous version, compared to ordinary fuzzy sets. In that article, the objective importance criteria weights and fuzzy group MCDM problems are determined with a signed-distance-based method in a successful and resilient way.
These studies are summarized in Table 1. Consequently, the use of Interval Type-2 trapezoidal fuzzy numbers shows the benefits to represent alternative scores and the significance of miscellaneous criteria in MCDM.
| Researchers | Used methods | Focus area |
|---|---|---|
| (Baležentis & Zeng, 2013)46 | Fuzzy MULTIMOORA using Interval Type-2 fuzzy sets | Personnel selection; an extension to a crisp MULTIMOORE method. |
| (Cebi 2015)39 | Fuzzy TOPSIS using Interval Type-2 fuzzy sets | Facility location selection problem |
| (Celik, Bilisik, Erdogan, Gumus & Baracli, 2013) 26 | Fuzzy TOPSIS and GRA using Interval Type-2 fuzzy sets | Evaluation of public transportation and customers satisfaction |
| (Celik, Aydin & Gumus, 2014)42 | Fuzzy VIKOR using Interval Type-2 fuzzy sets | Evaluate customer satisfaction level for the rail transit network |
| (Chen, Chang & Lu, 2013)41 | Fuzzy QUALIFLEX using Interval Type-2 fuzzy sets | Medical decision-making problem; an extension to a traditional QUALIFLEX method |
| (Chen, 2014)47 | Fuzzy ELECTRE using Interval Type-2 fuzzy sets | Supplier selection problem |
| (Chen & Lee, 2010)24 | Fuzzy TOPSIS using Interval Type-2 fuzzy sets | Evaluation of the cars |
| (Ghorabaee, Amiri, Sadaghiani & Goodarzi, 2014)45 | Fuzzy COPRAS using Interval Type-2 fuzzy sets | Supplier selection problem |
| (Kahraman, Öztayşi, Sarı & E. Turanoğlu, 2014)44. | Fuzzy AHP using Interval Type-2 fuzzy sets | Supplier selection problem |
| (Kuo, 2011)43. | Fuzzy VIKOR and GRA using Interval Type-2 fuzzy sets | Evaluation of service quality of Chinese cross-strait passenger airlines |
| (Naim & Hagras, 2014)21. | Fuzzy TOPSIS using Interval Type-2 fuzzy sets | Illumination selection in an intelligent shared environment |
Summary of recent researches on MCDM studies using Interval Type-2 fuzzy sets.
4.2. Method
This paper will use an Interval Type-2 TOPSIS technique, which is a modified version of the method proposed by Chen and Lee24. The steps of the applied approach are as follows: Step 1: Form a group of experts with k members and set the alternatives and evaluation criteria. Step 2: Establish the evaluation matrix by determining the linguistic variables for weighting criteria and the linguistic ratings for the alternatives as given in Table 2.
| Linguistic terms for the weights of the attributes | Linguistic terms for the ratings | Interval Type-2 fuzzy sets |
|---|---|---|
| Very Low (VL) | Very Poor (VP) | ((0, 0, 0, 0.1; 1, 1), (0, 0, 0, 0.05; 0.9, 0.9)) |
| Low (L) | Fairly Poor (FP) | ((0, 0.1, 0.1, 0.3; 1, 1), (0.05, 0.1, 0.1, 0.2; 0.9, 0.9)) |
| Medium Low (ML) | Poor (P) | ((0.1, 0.3, 0.3, 0.5; 1, 1), (0.2, 0.3, 0.3, 0.4; 0.9, 0.9)) |
| Medium (M) | Moderate (M) | ((0.3, 0.5, 0.5, 0.7; 1, 1), (0.4, 0.5, 0.5, 0.6; 0.9, 0.9)) |
| Medium High (MH) | Good (G) | ((0.5, 0.7, 0.7, 0.9; 1, 1), (0.6, 0.7, 0.7, 0.8; 0.9, 0.9)) |
| High (H) | Fairly Good (FG) | ((0.7, 0.9, 0.9,1; 1, 1), (0.8, 0.9, 0.9, 0.95; 0.9,0.9)) |
| Very High (VH) | Very Good (VG) | ((0.9, 1, 1,1; 1, 1), (0.95, 1, 1,1; 0.9, 0.9)) |
Linguistic terms and their corresponding Interval Type-2 fuzzy sets.
Step 3: Build the decision matrix Yp of the pth decision-maker produced from Table 2 and constitute the average decision matrix
Then construct the ranking weighted decision matrix

Flowchart of the proposed method.
Figure 2 represents the Interval Type-2 linguistic variables of our case study.
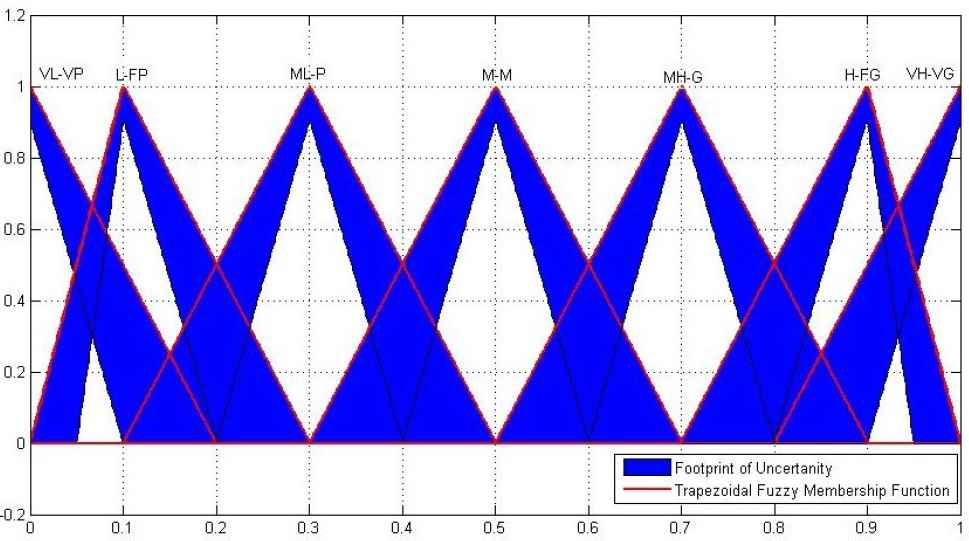
Representation of Interval Type-2 linguistic variables.
5. A case study: Evaluation of KM tools alternatives
In this real case, the DMs of ABC Company†, an international firm’s Turkish branch, are assisted by the proposed evaluation framework in deciding which KM product to purchase. ABC Company offers knowledge-based products, systems and solutions, giving internal KM extraordinary importance. ABC Company’s business model is IT-driven. Therefore, knowledge and its effective management is of utmost importance. There are also other good reasons why ABC Company is looking for a suitable KM product. ABC Company is a global firm and its employees share information by means of various methods besides face to face communication. KM tools involve technology enabled repositories and sharing networks which can help ABC Company to overcome geographical barriers. Changing customer expectations and new market offerings present another motivation for the lookout for a KM solution. Based on these reasonings, ABC Company decided to implement a KM system internally so that its staff can easily access and manage its corporate knowledge and gain experience.
Step 1: The selection of the most suitable KM tool is done by five professionals (DMs) within ABC Company. The composition of the decision committee is as the following. One member is a top manager because the top managers’ active involvement in the KM system adoption process greatly increases its success. Two members are chosen from the IT department based on their experience in corporate change management projects. The other two decision makers are senior managers of the company, who are potential users of the KM tools in future.
Step 2: The KM system selection requires the committee to select a product among others that matches well with the internal needs and requirements. The selected KM system shall also be in line with corporate guidelines and IT architecture, leaving the committee with the following alternatives: IntelliEnterprise by Adenin Technologies (alternative a1), SharePoint by Microsoft (alternative a2) and Oracle Beehive by Oracle (alternative a3). The evaluation criteria are determined as it is summarized in Table 2.
Step 3: Firstly, we start to build up three decision matrices Y1, Y2 and Y3 for three alternatives a1, a2 and a3, respectively. Afterwards, we compute the average decision matrix Ỹ in order to have the corresponding Type-2 representations as follows;
Step 4: We calculate the average weighting matrix
Step 5: We compute the weighted decision matrix ỸW;
Step 6: Firstly, we construct the ranking weighted decision matrix
We obtain the following matrix;
Representation of the alternatives by the evaluation of 5 different experts x1,x2,x3,x4 and x5.
Secondly, we apply the ranking method proposed by Chen and Lee24 and obtain the following matrix;
Step 7: We start to calculate the positive x+ and the negative x− ideal solutions for both methods.
The ideal solutions with the centroid approach are;
Furthermore, we find the ideal solutions based on the method Chen and Lee24;
Step 8: In order to sort the results we start to calculate the distances between each alternative and both ideal solutions.
Moreover, we repeat the same procedure for the method of Chen and Lee24 and we find the following results;
These values are illustrated in Figure 2. It seems that our method offers small values for distances.
Step 9: We calculate the degree of closeness of each alternative C(a1)= 0.64 C(a2)= 0.42 C(a3)= 0.46
Afterwards, we find the degrees of closeness by the method of Chen and Lee; C(a1)= 0.64 C(a2)= 0.43 C(a3)= 0.45
Step 10: Finally, we sort the degrees of closeness. For both approaches, we find that C(a1) > C(a3) > C(a2). Consequently, we conclude that a1 is the best choice.
5.1. Comparative analysis and discussion
In this part of our study, the effectiveness of the proposed method is validated with other approaches. Our seven scale linguistic terms are used to measure the variations within the KM framework. In this section, we will compare our proposed method with Type-2 fuzzy TOPSIS method proposed by Chen and Lee24, Type-1 TOPSIS proposed by Chen et al.48 and classical crisp TOPSIS.
The first analysis was achieved using the method of Chen and Lee24. We applied their developed Type-2 Fuzzy TOPSIS method to obtain rankings in KM problem. Two methodologies yielded similar ranking results, however the positive and negative distances were different. In our proposed method, the distances were found to be approximately two times smaller than Chen and Lee24.
The second comparative analysis was performed with the fuzzy TOPSIS method of Chen et al.48. This pioneering study highlighted an extended method of classical TOPSIS to study the supplier selection problem. They started with the use of linguistic variable in order to assess the status of each supplier through the corresponding closeness coefficient. Our comparison with this approach concluded the similar rankings. However, the values of Chen et al.48 for the closeness were approximately two times smaller than our method.
The last comparative analysis concerns the computation of the classical crisp TOPSIS method. We obtained the similar ranking for the closeness, but our findings were found to be smaller.
Finally, the proposed Type-2 Fuzzy TOPSIS method which is based on the centroid method is found to be consistent in KM framework. All methods give a1 > a3 > a2 for the ranking. As all comparative results indicate the validity of our method, the ranking of the alternatives do not differ, but the scale of optimum distances might vary. Moreover, we note that the proposed method provides stable decisions and does not need additional steps. Therefore, we might conclude that it is distinguishable among the existing MCDA applications.
6. Conclusion
The importance of KM tools is increasing within the realms of corporate world, as competitive business environment forces businesses to operate more efficiently and effectively. There exist many solutions for companies seeking KM solutions, however the question remain which of these solutions fits best to the specific needs of the organization.
This study proposed a group decision framework based on the Interval Type-2 fuzzy TOPSIS method for evaluating and selecting a suitable KM tool. In order to check the usability of the proposed framework, it is applied in a real case of company. It should be emphasized that although the proposed framework is developed for this specific KM tool selection problem, it can also be extended to evaluate other kinds of software.
In our study, we integrated the new centroid based ranking method of Wu and Mendel36 asanew approach for Interval Type-2 fuzzy TOPSIS analysis. This method considers the centroids of the Interval Type-2 fuzzy sets. We preferred to use this method as it satisfies all Type-2 properties and it seems to be more feasible in large scale terms with respect to other methods. It is also notable that this method provides a robust analysis in comparative studies. Furthermore, we compared our study with the method proposed by Chen and Lee24. This step included the substitution of ranking method of Wu and Mendel36. For the following steps, we remarked that our approach provided more normalized values. On the other hand, both methods offered same ranking order. Finally, we conclude the same remark of Wu and Mendel36 by stating that our method could be an alternative choice in Type-2 TOPSIS studies. As future research, the methodology based on Interval Type-2 fuzzy logic can be combined with other MCDM techniques on the problem of KM tool selection, and results can be compared to the findings of this article.
7. Acknowledgment
The authors would like to kindly thank for the financial contribution of the Galatasaray University Research Fund (Projects 14.402.004 and 15.402.003), for the support of ABC Company and its KM system selection committee members.
Footnotes
To provide anonymity, we name this company as Company ABC.
References
Cite this article
TY - JOUR AU - Gülçin Büyüközkan AU - Ismail Burak Parlak AU - A. Cagri Tolga PY - 2016 DA - 2016/09/01 TI - Evaluation of Knowledge Management Tools by Using An Interval Type-2 Fuzzy TOPSIS Method JO - International Journal of Computational Intelligence Systems SP - 812 EP - 826 VL - 9 IS - 5 SN - 1875-6883 UR - https://doi.org/10.1080/18756891.2016.1237182 DO - 10.1080/18756891.2016.1237182 ID - Büyüközkan2016 ER -
