Multi-UAV Cooperative Task Assignment Based on Orchard Picking Algorithm
 , Xin Zheng1, Harish Garg2,
, Xin Zheng1, Harish Garg2, 
- DOI
- 10.2991/ijcis.d.210423.003How to use a DOI?
- Keywords
- Multi-objective optimization; Cooperative task assignment; Heterogeneous UAVs; Nearest neighbor method; Orchard picking algorithm
- Abstract
The multi-unmanned aerial vehicle (UAV) must autonomously perform reconnaissance-attack-evaluation tasks under multiple constraints in the battlefield environment. This paper proposes a nearest neighbor method designed with the shortest neighboring distance as an indicator which quickly solves the optimal sequence of multiple tasks for cooperative execution. Each target to be destroyed requires a different quantity of ammunition; a cooperative task assignment model for heterogeneous UAVs is established accordingly. Based on the nearest neighbor method, and with reference to fruit-picking techniques currently in use, a novel “orchard picking algorithm (OPA)” is investigated as well. This algorithm proposed in this paper is a heuristic algorithm, which has a broad application prospect in complex task assignment. A cooperative attack task assignment is simulated to test the performance of the algorithm. In essence, it balances the assignment of tasks, works within a brief execution time, and exhibits high flexibility, strong robustness, and scalability.
- Copyright
- © 2021 The Authors. Published by Atlantis Press B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
The unmanned aerial vehicle (UAV) has the advantages of strong continuous combat capability, high maneuverability, and environmental adaptability due to the fact that they are not controlled by pilots [1–4]. In the process of actual combat, due to the complex and varied environment and wide distribution of targets, it usually requires multiple UAVs to cooperate with each other to carry out tasks [5], which makes the task execution time shorter and the completion rate higher [6,7]. Optimal decisions need to be taken for various mission-critical operations performed by UAVs [8]. The assignment of cooperative tasks to multi-UAVs refers to strategical execution of reconnaissance, attack, evaluation, and more for multiple targets within a certain area for multiple homogeneous or heterogeneous UAVs, thus maximizing the overall success of combat. The effectiveness of cooperative task assignment to multiple UAVs is an important indicator of the combat capability of UAVs.
Previous scholars have established various algorithms for the assignment of cooperative tasks to multi-UAVs. Author(s) [6–9], for example, proposed the fast task assignment (FTA) method algorithm based on Q-learning by neural network approximation and experience replay sequencing, which effectively transferred online computing to an offline learning process to assign tasks to heterogeneous UAVs under the condition of environmental uncertainty. A brain storm optimization was improved by local search procedure that each new candidate solution moves to the local best position thus reducing computational time [10]. Jia et al. [11] took the two-stage stochastic programing model as a research object to transform the problem of optimizing combinations of heterogeneous UAVs into a problem of assigning cooperative multi-tasks with random speeds and time windows. They established a heuristic algorithm based on improved genetic algorithms accordingly [7,12,13]. A new prediction strategy was proposed based on center points and knee points under an adaptive diversity maintenance strategy [14]. A number of random individuals corresponding to the difficulty of the problem are generated to maintain proper population diversity and this is an effective evolutionary dynamic multi-target optimization method.
A new multi-objective genetic algorithm was proposed recently which is based on a mixed fitness function and Pareto-based measures [15]. The optimal solution is sought to resolve complex task programing with regard to UAVs and ground control systems [16,17]. The algorithms cannot be programed online in real time, however, making it difficult to respond to sudden threats. In an effort to remedy this, Ziyang Zhen et al. [18] explored cooperative search-attack tasks with dynamic targets and threats and they proposed a distributed intelligent self-organizing task planning algorithm for multiple UAVs accordingly.
Many targeted heuristic algorithms have been applied to solve multi-target optimization problems in recent years [19–21], but there is currently no general cooperative task assignment model that can simultaneously meet complex battlefield environments with coupled task relationships and strict requirements for the task timing sequence. Although existing algorithms cannot guarantee optimal results, they do provide satisfactory solutions within an acceptable time period [22,23]. As the scale of the problem increases, the amount of algorithm calculation increases exponentially and thus the calculation time increases significantly [24]. However, most previous researchers have set cost functions according to the importance of the target and the capabilities of the UAVs in the process of multi-task assignment. Only the requirements of the task group for the number of UAVs is given, which does not account for the essential characteristics of the tasks.
When implementing cooperative reconnaissance, attack, and evaluation tasks, multiple unmanned aerial systems need to consider their own load constraints, mission sequence, and target position. Multi-UAV systems perform multiple tasks in the face of multiple targets, it will be better to find an algorithm with short computation time and balanced allocation. The purpose of the present study is to develop a practical algorithm to directly assign tasks for multiple targets with different needs. Inspired by the efficiency with which fruit farmers harvest their product, a novel multi-task assignment algorithm was established which regards the target group as “fruit trees,” the target characteristics as “fruits” of varying dimensions, and the UAVs performing tasks as “fruit farmers” picking the “fruit” according to the optimal strategy. The multi-task distribution is thus completed accurately at an acceptable cost.
The organizational structure of the paper is as follows. Section 2 establishes a multi-task model based on the nature of the multi-UAV tasks. Section 3 discusses the targets, realizations, and optimal evaluation indexes. Section 4 outlines the principle of the orchard picking algorithm. Section 5 gives the results of the simulation conducted to test the proposed method. Section 6 provides a brief summary and conclusion.
2. ESTABLISHMENT OF MODELS
The multi-target reconnaissance-attack-evaluation tasks were modeled first, then the corresponding parameters of UAVs and tasks were defined. Constraints were placed appropriately on the reconnaissance-attack-evaluation task planning mode [25], then mathematical expressions for the problem of task assignment in question were established as discussed in detail below.
2.1. Background Description
If the position of the enemy target group on the battlefield is known, it is necessary to perform reconnaissance-attack-evaluation tasks for the enemy target group. Each target needs at least one device for detailed reconnaissance and at least one type of ammunition for each target to be destroyed. Likewise, at least one image acquisition device is required for each target to be evaluated.
There is no coupling relationship between various tasks in this case, that is, each task can be executed in the order of reconnaissance, attack, and evaluation. If each UAV can carry only one reconnaissance device, one type of ammunition, or one image acquisition device, all the UAVs that perform tasks jointly form a heterogeneous UAV group. The modern battlefield has harsh environment and strict, brief timeline characteristics. To function properly in this environment, the UAVs must complete specified tasks in the shortest possible time.
2.2. Definition of Symbols
Reconnaissance, attack, and evaluation are the main UAV tasks during battle, and there are timing constraints between the three types of tasks. The two triples discussed here represent the amount of ammunition for the target to be completely destroyed and the UAV ammunition loading capacity, respectively. The triplet is the set of the target task demands and
It should be noted that the target's demand for UAVs is not only quantitative but also relates to the load properties. It is not appropriate in this case to assign weight to the target value using the method presented above in the Introduction section. Whether the task can be fully executed depends on the geometric relationship of the two triples, that is, for
Consider the UAV cooperative attacks as an example. It is necessary to satisfy
It is worth noting that the above symbol definition directly quantifies the target's property requirements rather than assigning weighted values, as is typically the case. The solution result so sought is more realistic. Similarly, this method is also applicable to task assignment in cooperative reconnaissance and cooperative evaluation contexts, which are not described in detail here.
2.3. Mathematical Modes
The assignment of cooperative tasks to multi-heterogeneous UAVs can be expressed as a combinatorial optimization problem [26]. The total number of q type missiles required for all targets to be destroyed is
Equations (1) and (2) represent the sum of the type of ammunition and the amount of ammunition required for all enemy targets to be completely destroyed. The resources carried by the task-performing UAVs must not be fewer than the required quantity.
There are a total of Nu heterogeneous UAVs. Each type of UAV can only carry one type of missile. There are a total of
The total amount of missiles carried by all UAVs performing tasks is
If all targets can be destroyed, the amount of ammunition carried by the UAVs scheduled to perform the task is not less than the amount of ammunition required for the targets to be destroyed. Thus,
Formula (5) gives the constraint relationship between the total demand of the task and the total load capacity of the UAV. The purpose of this work is to cooperatively program local tasks under the overall constraint framework. Accordingly, for the multi-task and multi-constraint problem, a task assignment strategy directly specific to the task sequence was established.
3. ANALYSIS OF PROBLEMS
3.1. Relationship Between Capabilities
Formula (5) can only guarantee the overall combat capability required by the UAV under the condition that all targets are completely destroyed. The task sequence and execution strategy cannot be obtained by this formula.
The battlefield environment is highly complex and destroying the target group in the shortest amount of time possible is the key to victory in combat. Thus, maximum efficiency (i.e., “the shortest time”) is taken the optimal evaluation index in this study. Without considering the time spent by the UAV to drop ammunition, the path from the initial position to the target position is the shortest possible and accordingly the time required to complete this task is also the shortest.
The UAV i carrying the p-type ammunition flies from the base to the targets
The amount of ammunition carried by each UAV cannot always meet the amount of ammunition required by the target in an integer. In other words, there is always one target that requires cooperative attacks by multiple UAVs or one UAV that can attack multiple targets in a real-world combat scenario.
3.2. Optimal Evaluation Indexes
The set Sp determines the strategy used by a UAV to perform its tasks. Any UAV i carrying type p ammunition performs a given mission according to the target sequence s. The range from the base to the completion of the task is
Equation (9) considers the urgency of the combat task to be completed within the shortest possible range. Therefore, the optimal programing of the task set
3.3. Task Sequence
According to the model presented above, a nearest-neighbor method was established in this study based on the shortest adjacent target range and compared against another method which solves large-scale, multiple traveling salesman problems via ant colony-Partheno genetic algorithms. Under this method compared against the proposed method [14], the multi-target optimization problem is regarded as a large-scale multi-traveling salesman problem. The task sequence of the Nt targets solved is expressed as
The multi-traveling salesman problem centers on the shortest distance traveled by the salesman who travels from the starting target, passes by several required targets, and reaches its respective termination targets on the premise of the minimum and maximum requirements of the number of “cities” that each salesman must visit. However, in an actual battlefield, time is one of the most important measures of task effectiveness; performing all tasks in the shortest time possible is the most effective strategy.
The nearest-neighbor strategy proposed in this paper comes always at the cost of an increase in the range of returning by the UAV after it completes the task. The closest next target is always selected, namely,
The description of the target demand in the model has an additional dimension qk, so the original binary variable becomes the ternary variable
4. THE ORCHARD PICKING ALGORITHM
Bionic algorithms have been used increasingly frequently in recent years to solve multi-target optimization problems [27] and generally provide satisfactory solutions. A novel algorithm for cooperative attacks on multiple targets by multiple UAVs was established in this study as inspired by fruit-picking methods.
Multiple fruit trees are distributed in an orchard of a certain area. Each fruit tree bears different numbers of fruits of different sizes. There are multiple fruit farmers carrying a pack basket that can hold a certain number of fruits. Each farmer can only pick fruits of one certain diameter and is required to complete the picking task in the shortest possible time. This is a problem of optimal assignment. The “picking time” is directly related to the speed at which the farmer walks, the size of his basket, the number of fruit trees, the yield of the fruit, the distance between the warehouse and the orchard, etc. The fruit-picking process was evoked in establishing the proposed algorithm to solve the problem of multi-target assignment in cooperative attacks by multiple UAVs.
4.1. Algorithm Modeling
Assume that the area of the orchard has a range within which Nf fruit trees are distributed. The position distribution of each tree is known. According to the difference in fruit diameters, the fruits to be picked are divided into Nd species. There is a total of Np fruit farmers engaged in picking. Due to the limitation of picking tools, each fruit farmer can only pick fruit of a single diameter—there is also an upper limit on the number of fruits that can be carried by each farmer. A farmer returns to the warehouse (base) only when his basket is full.
According to the actual situation, each fruit farmer has a different walking speed, and the walking speed of the i-th fruit farmer is
4.2. Analysis of the Algorithm
Naturally, each fruit tree has a singular and constant location. The closer it is to the warehouse, the shorter the time it takes to pick; it is also picked faster by a farmer who walks at a greater speed. Efficiency is also greater if a farmer picks a larger number of fruits in a single picking iteration, and/or if a greater number of farmers are engaged in the picking process. Each farmer selects the tree closest to his current location or closest to the warehouse for picking depending on the current carrying capacity of his basket, the distribution of nearby trees, and the number of fruits on them. In other words, the picking task for each farmer is locally optimal.
According to the previous assumptions, the total task load of picking Ti for the i-th farmer is
As the information on the k-th diameter is already included in
Each farmer uses the optimal available plan to complete the picking process, i.e., whichever approach allows him to fill his basket the quickest. This is exactly the result desired to solve the problems raised in the multi-UAV problem at the center of the present study.
5. SIMULATION AND VERIFICATION
5.1. Description of Problems
The proposed orchard picking algorithm was numerically simulated to test its performance. It was assumed in this case that the distribution of the target positions was as shown in Table 1. The types of ammunition (three in total) and quantity distribution required for target destruction were as shown in Table 2. If both the quantity of UAVs and ammunition at the base are sufficient, multiple heterogeneous UAVs carry different types and quantities of ammunition to cooperatively attack a target group in a certain area. Considering the inherent urgency of the battlefield and the need to take into account combat costs, once a task begins, the UAV does not return to the base to replenish its ammunition.
| Target | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 |
|---|---|---|---|---|---|---|---|---|---|
| X | 26 | 83 | 71 | 37 | 59 | 29 | 84 | 55 | 61 |
| Y | 38 | 85 | 88 | 24 | 72 | 85 | 49 | 26 | 38 |
Distribution of coordinate positions of target group (unit: km).
| Target | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 |
|---|---|---|---|---|---|---|---|---|---|
| A1 | 3 | 2 | 2 | 3 | 0 | 2 | 2 | 3 | 3 |
| A2 | 1 | 3 | 1 | 0 | 2 | 2 | 0 | 2 | 3 |
| A3 | 2 | 0 | 2 | 2 | 3 | 1 | 3 | 2 | 0 |
Types and quantities of ammunition required for target group to be attacked (unit: type and quantity).
There are also three types of UAVs corresponding to the three types of ammunition. It is assumed that the UAV carrying A1 ammunition can carry 6 A1s, the UAV carrying A2 ammunition can carry 4 A2s, and the UAV carrying A3 ammunition can carry 4 A3s. The three types of UAVs have the same flight speed, 180 km/h, and a maximum flight time of 6 hours. The base coordinate position is (10 km, 10 km) and the number of UAVs is sufficient. According to the calculation process outlined above, at least 4 UAVs carrying A1 ammunition, 4 UAVs carrying A2 ammunition, and 4 UAVs carrying A3 ammunition should be flown.
5.2. Solving Task Sequence
The above problem was also converted into a multi-traveling salesman problem [14] to form a reference sequence for the shortest range: base→ T4 → T8 → T9 → T7 → T2 → T3 → T5 → T6 → T1. The task profile determined according to the traveling salesman algorithm as shown in Figure 1.

Task profile based on multiple traveling salesman problem.
According to the nearest-neighbor method proposed here, when the UAV performs multiple tasks, it always selects the target closest to the current position. The reference sequence is thus base → T4 → T8 → T9 → T7 → T5 → T3 → T2 → T6 → T1. A solution is derived according to the proposed algorithm on the task profile shown in Figure 2.
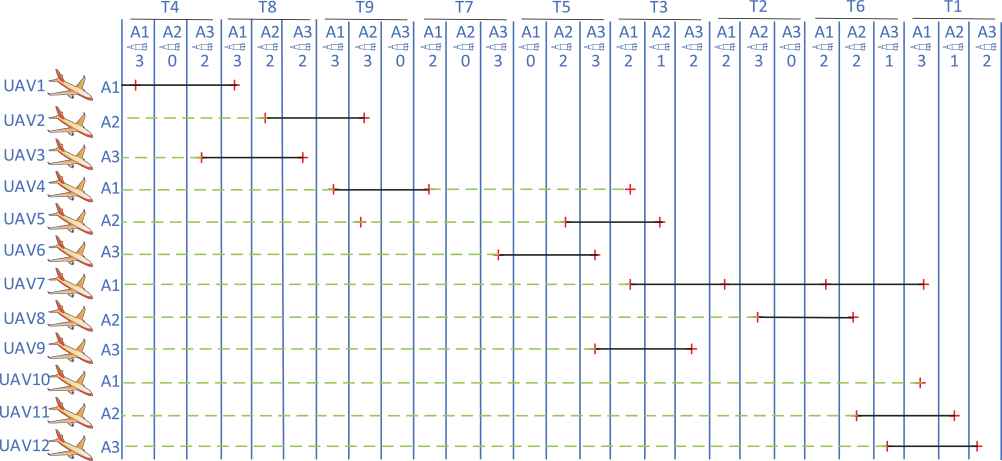
Task profile based on nearest-neighbor method.
As shown in Figures 1 and 2, the traveling salesman [14] and nearest-neighbor method can both solve the task sequence. The former is based on overall optimization and the latter is mainly based on local optimization. In each method, the seventh UAV has the largest task load and is responsible for the targets T2, T3, T6, and T1. Accordingly, compared with other UAVs, it has a longer range and takes the longest time to complete its task. The locally optimal task assignment scheme of either reference sequence can be obtained by the orchard picking algorithm.
5.3. Analysis of Results
The nearest-neighbor method proposed in this paper is nearly identical to the task reference sequence obtained by the traveling salesman method. The difference is that the former involves making minor adjustments to part of the task sequence and requires manual intervention to ensure a strategic task assignment. In order to prove the superiority of the orchard picking algorithm, this paper also takes particle swarm optimization algorithm and tabu search algorithm as the control group to solve the above problems respectively. The four methods were compared according to important indexes as shown in Table 3.
| Evaluation Index | Task Rate % | Task Time s−1 | Total Range km−1 | Return Range km−1 | Total Range km−1 | Total Voyage Time h−1 |
|---|---|---|---|---|---|---|
| MTSP method | 100 | 1.146 | 1256.213 | 753.075 | 2009.288 | 11.163 |
| PSO method | 100 | 1.324 | 1281.867 | 780.849 | 2062.716 | 11.460 |
| TS method | 100 | 1.285 | 1246.451 | 803.216 | 2049.667 | 11.387 |
| Method proposed | 100 | 0.810 | 1075.293 | 925.078 | 2000.371 | 11.113 |
Comparison of task performance between two methods.
As shown in Table 3, when the same number of UAVs is deployed and the same amount of ammunition is given, both the nearest-neighbor method proposed in this paper and the method proposed in [18,23] can complete the task assignment. The total range of each method is about 2000 km and the total flight time is about 11 h. On the whole, both methods consume approximately the same amount of energy as well. The proposed method did not dramatically outperform the other method in this case. Particle swarm optimization algorithm and tabu search algorithm perform well in single task assignment, e.g., only attack task is performed without considering return time. However, in the implementation of the multi-task and multi-constraint problem of reconnaissance, attack, evaluation, and return trip with time constraints, these two algorithms are not as good as the orchard picking algorithm proposed in this paper.
It is worth noting, however, that in terms of task completion time, the nearest-neighbor method is significantly better than the traveling salesman method [14,22]. The task completion time of the former is 1.146 h while that of the latter is only 0.810 h, marking time savings of 29%. In an actual combat scenario, the proposed method would result in the destruction of all enemy targets in a shorter time than the traveling salesman method. In order to verify the superiority of the algorithm proposed in this paper, the data used in the simulation experiment are simplified according to the actual battlefield target distribution. The orchard picking algorithm proposed in this paper not only considers the attributes of the task, but also considers the location distribution of the target group, which is an important index considered by the algorithm.
The primary evaluation criterion for task completion in this case is the time necessary to complete the last task, which depends on the UAV that performs the most tasks and has the largest range. An analysis of the relationship between target completion quantity and time is shown in Figure 3.
The results of the traveling salesman method and the proposed nearest-neighbor, orchard picking method are both satisfactory, as shown in Figure 3. The time spent to complete the task gradually increases with the number of targets to be attacked. The task assignment of the latter is relatively uniform and the number of targets is approximately linearly related to the execution time. This is because the nearest-neighbor method can alter its task assignment strategy during execution. Due to the constraints of task sequence and return time, the optimization space of particles is no longer continuous, resulting in the longest convergence time of the particle swarm optimization algorithm. Tabu search algorithm can select the corresponding tabu search region according to the task constraints, which converges faster than particle swarm optimization algorithm, but it is easy to cause premature convergence, and it is difficult to find the optimal solution. The orchard picking algorithm proposed in this paper can quickly search for the optimal solution in discontinuous space without local oscillation, and the convergence rate of the algorithm has an approximate linear relationship with the task size. As shown in Table 3, as there are slight differences between the total ranges. Increasing the return range cost reduces the task execution time, thereby ensuring that the UAV can complete the cooperative attack of multiple targets in the shortest possible time.
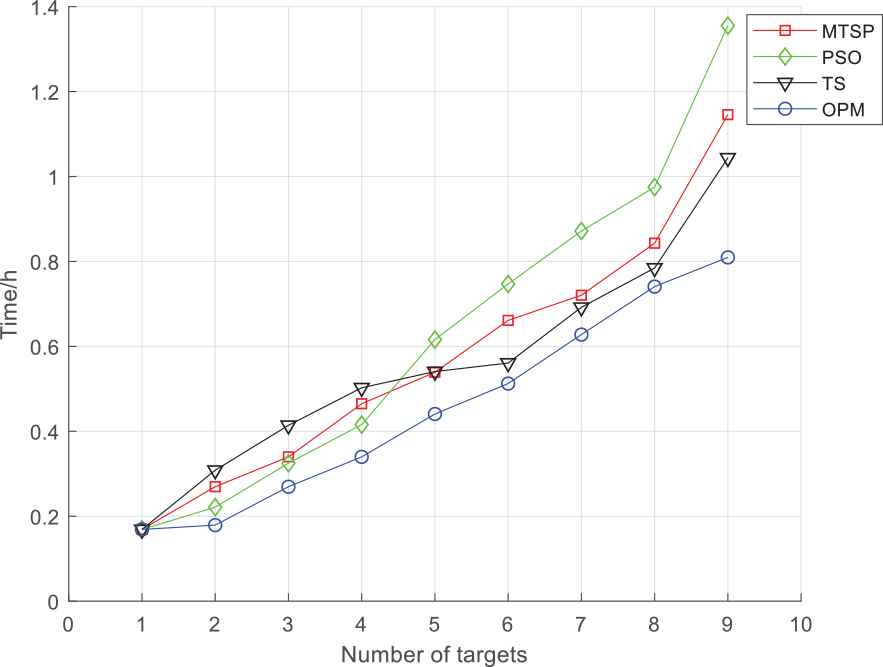
Comparison of the four approaches.
6. CONCLUSIONS
This study was conducted to establish a novel method for assigning tasks to heterogeneous UAVs in a time-critical combat environment. Multiple targets and multiple tasks were denoted as fruits on multiple fruit trees to be picked in an effort to mimic the strategy used by farmers to harvest product. The orchard picking algorithm was established accordingly to solve the multi-target optimization problem. The algorithm works well under the given task requirements, avoids setting a complex cost function based on the tasks, and has high calculation efficiency.
A nearest-neighbor method was also established for the multi-task sequence with the shortest current distance as an index. Compared with the global optimal multi-traveling salesman problem, this method maintains the local optimum at all times. The orchard picking algorithm proposed in this paper can deal with the time series constraints of different tasks well, and the convergence time is faster than that of particle swarm optimization algorithm, and it does not fall into local optimum as easily as tabu search algorithm. It also works at a significantly lower task execution time on the premise that the total consumption remains almost unchanged. In future research, an adaptive strategy of task cooperative assignment will be introduced on the basis of the orchard picking algorithm proposed in this paper, so that the task load of each UAV is relatively balanced to adapt to the battlefield situation in real time.
CONFLICTS OF INTEREST
The authors declare they have no conflicts of interest.
AUTHORS' CONTRIBUTIONS
Weiheng Liu, Xin Zheng and Harish Garg conceived and worked together to achieve this work. Weiheng Liu was responsible for investigation, conceptualization, methodology, analysis and writing original draft. Xin Zheng was responsible for conceptualization, validation, supervision, and funding acquisition. Harish Garg was responsible for conceptualization and analysis. All the authors wrote, edited and revised the article.
ACKNOWLEDGMENTS
The authors are indebted to the editor and anonymous reviewers for their helpful comments and constructive suggestions. The authors wish to thank China Aerospace Science and Engineering Group for providing research facilities. This work was sponsored by Hiwing Aviation General Equipment Co., Ltd, Aerospace Science and Engineering Group.
REFERENCES
Cite this article
TY - JOUR AU - Weiheng Liu AU - Xin Zheng AU - Harish Garg PY - 2021 DA - 2021/04/29 TI - Multi-UAV Cooperative Task Assignment Based on Orchard Picking Algorithm JO - International Journal of Computational Intelligence Systems SP - 1461 EP - 1467 VL - 14 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.210423.003 DO - 10.2991/ijcis.d.210423.003 ID - Liu2021 ER -
