Three-Dimensional Multi-Mission Planning of UAV Using Improved Ant Colony Optimization Algorithm Based on the Finite-Time Constraints
 , Xin Zheng
, Xin Zheng- DOI
- 10.2991/ijcis.d.201021.001How to use a DOI?
- Keywords
- Improved ant colony optimization; Variable dimension vector coefficient; Three-dimensional missions planning; Time adaptive factor; Finite-time constraints
- Abstract
An improved ant colony optimization (IACO) is proposed to solve three-dimensional multi-task programming under finite-time constraints. The algorithm introduces the artificial preemptive coefficient matrix into the transfer probability formula, which makes results convergence and also reduces the convergence time of the algorithm. Following the principle that there is no pheromone on the path where the ants are just beginning to forage in reality, the pheromone is initially zero, and the ant's self-guided ability is fully utilized, which enhances the random exploration ability of the ant algorithm for the entire solution space. By introducing the variable dimension vector coefficient and the time adaptive factor of transfer probability, the search probability in the inferior solution set is reduced and the convergence speed of the algorithm is increased. Finally, through the simulation on the random map and comparison with the traditional ant colony optimization, particle swarm optimization, and tabu search algorithm, the superiority of the IACO proposed in this paper is demonstrated.
- Copyright
- © 2021 The Authors. Published by Atlantis Press B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
With the rapid development of unmanned aerial vehicle (UAV) technology, intelligent UAV will have greater prospects for future military and civilian applications, especially significant researching in the future battlefield or under extreme circumstances to replace human work. At present, the research on UAV mission planning mainly focuses on the task allocation in two-dimensional space. According to the characteristics of the task, the intelligent optimization algorithm is used to solve the problem [1,2], and a series of optimal or suboptimal sequence points are generated within a limited time. Finally, a feasible track is generated by the Dubins path, PH path, and Clothoid path method. Shortest path problem is a classical problem in computer science but many inspired algorithms suffer from a low converge speed. To solve this problem, a Bayesian iteration rule is proposed in [3]. In the actual battlefield conditions, UAV must face a variety of uncertain environments such as peaks, ravines, weather, and enemy threats and it must also consider constraints such as range, flight altitude, and concealment, as well as the time-coupled characteristics of missions. Three-dimensional task assignment based on finite-time constraints in complex random environments is the premise for the intelligent implementation of UAV, except for the comprehensive consideration of the environmental information, dynamics, and kinematic constraints of UAVs, and it also considers the order, time and cost of the tasks performed by the UAV, as well as the solving time and the stability of results.
Traditional UAV mission planning uses heuristic algorithms, such as genetic algorithm (GA), particle swarm optimization (PSO), simulated annealing algorithm, tabu search (TS) algorithm, and ant colony optimization (ACO), all of which are inspired by certain phenomena and laws of nature. A bio-inspired method was proposed to address transportation network design, which adopts a physarum-inspired algorithm with sequential attractants, and utilizes the gravity model to predict transportation flux in each city pair [4]. The main factors extracted to form the mathematical model are used to solve the combinatorial optimization problem in mathematics, and the optimal or suboptimal solution is given within a reasonable time. A network dividing method is presented inspired by the natural phenomena of bacterial growth, division, and competition [5]. In solving discrete problems, GAs are more commonly used, but the Hamming cliff problem is easy to appear [6]. In solving the extremum problem in the number domain, the particle swarm algorithm is more commonly used because the computational programming is simple and the problem is solved quickly. The disadvantage is that it is easy to trap into local optima [7], and the algorithm cannot obtain the optimal solution. In solving large-scale combinatorial problems, simulated annealing algorithm is a kind of powerful local search ability with short running time [8]. However, there is a problem that is greatly affected by the initial parameters and the overall searchability is poor. The ACO is simple and scalable [9]. It is used to solve symmetric TSP and asymmetric TSP, as well as assignment problem and vehicle-scheduling problem. It has in-depth research and application both from theory and application.
This paper deals with the problem of multi-target task planning based on finite-time constraints in random 3D maps and proposes an improved ant colony optimization (IACO) based on other algorithms based on finite-time constraints with the advantages of other algorithms, so an IACO is proposed. A typical non-deterministic polynomial (NP-hard) combination optimization problem of the on-wait flow shop is solved by the original hybrid ACO based on the mechanism of crossover and mutation [10], which has combined the idea of a gene with replication, crossover, and mutation to explore the next destination for the ants. Taking the dynamic properties of UAVs into account, Roberge [11] compared the complex, compute feasible, and quasi-optimal trajectories using the GA and the PSO algorithm. Perez-Carabaza [9] presented a novel method of IACO to explore the UAVs’ trajectories for a lost target in the minimum time. Kurdi [12] benchmarked the performance of the proposed approach about autonomous task allocation for multi-UAVs based on the locust and elastic behavior in response to impetus. Unmanned aerial vehicle systems can be a data acquisition platform in [13], and a measurement instrument for surveying of three-dimensional mapping. An improved distributed ACO algorithm [14], which is presented to carry out the mission planning and generate waypoints adopts the distributed control architecture which divides the global optimization problem into several local optimization problems. The vehicle routing problem with simultaneous pickup and delivery is a popular extension of basic Vehicle Routing Problem of NP-hard in real word [15], which has been solved by a hybrid metaheuristic algorithm based on a colony system and a variable neighborhood search.
At present, most of the UAV mission planning uses cost functions to simplify the calculations by turning complicate three-dimensional problem to a two-dimensional problem, but the use of height information and transcendental information is not sufficient, and the time constraints between actual mission points are not considered. The performance of the planned mission points after flight path optimization is poor, and the existing task planning algorithm is not universal and the convergence time is not stable. In this paper, an IACO is proposed for multi-mission planning under finite-time constraints in a random three-dimensional environment. The main contributions are as follows:
Based on the original ACO, the artificial preemptive coefficient matrix is added to the heuristic factor in the transfer probability formula, and the corresponding weights are set according to the order requirements of the task and the task group under finite-time constraints. On account of the normalization process improving the guidance of the solution space, the artificial preemptive coefficient matrix introduced accelerates the convergence time of the algorithm, avoids falling into local optimization, and improves the intelligence of the algorithm.
Following the law of ant foraging in practice, the pheromones at the beginning of each iteration are set to zero, which reduces human interference, ensures the autonomy of ants, and enhances the ability of ants to explore the entire solution space. Therefore, the probability of the optimal solution is raised in each iteration.
Introducing the variable dimension vector coefficient of probability transfer, the probability transfer formula is clustered, and the randomness of the exploring the entire solution space is increased in conjunction with artificial prior information and weak pheromones in the early stages of the algorithm. Then the probability of the optimal solution is further guaranteed.
The time adaptive factor of probability transfer is added. As the number of iterations increases, the modified algorithm can adapt the exploration strategy and self-guide more ants to search in noninferior solution space, thereby ensuring the optimal solution and improving the convergence speed.
Finally, through the simulation and comparison on a random map, the effectiveness of the IACO proposed in this paper is verified, and the requirements of multi-mission programming of drones in an unknown three-dimensional environment and under finite-time constraints are met. Compared with the traditional ACO, particle swarm algorithm and TS algorithm, the convergence time and optimal result have been improved significantly.
2. MULTI-MISSION MODEL DESCRIPTION
2.1. Selection Principle
The actual Battlefield where the UAV is located is extremely complex. It is necessary to consider both the natural geographical environment and the radar reconnaissance area and the fire threat area of the enemy. Taking the various influencing factors of actual operations into account, the complexity and difficulty of the model are increased, but the effectiveness of the algorithm is guaranteed. During the implementation of the mission planning for UAVs [16,17], the ups and downs of the terrain affect the climb and fall of the UAV, making UAV frequently accelerate and brake, which results in increasing the fuel consumption and reducing the concealment of the UAV. Due to the blocking of hills and peaks, UAV must turn and fly to the destinations, so the cost of the voyage must be increased. Setting the threshold
2.2. Problem of Tasks Coupling Constraints
To validate the feasibility and generality of the IACO proposed in this paper, any random points are arbitrarily generated on the abovementioned random map to carry out task planning in a three-dimensional map [11]. In the actual battlefield, the enemy's targets are often dispersed, that is, there is a chain effect between the mission points, so it is necessary to continuously attack the entire target group and minimize the enemy's resistance time. As shown in Figure 1, due to the inter-coupling of some task points
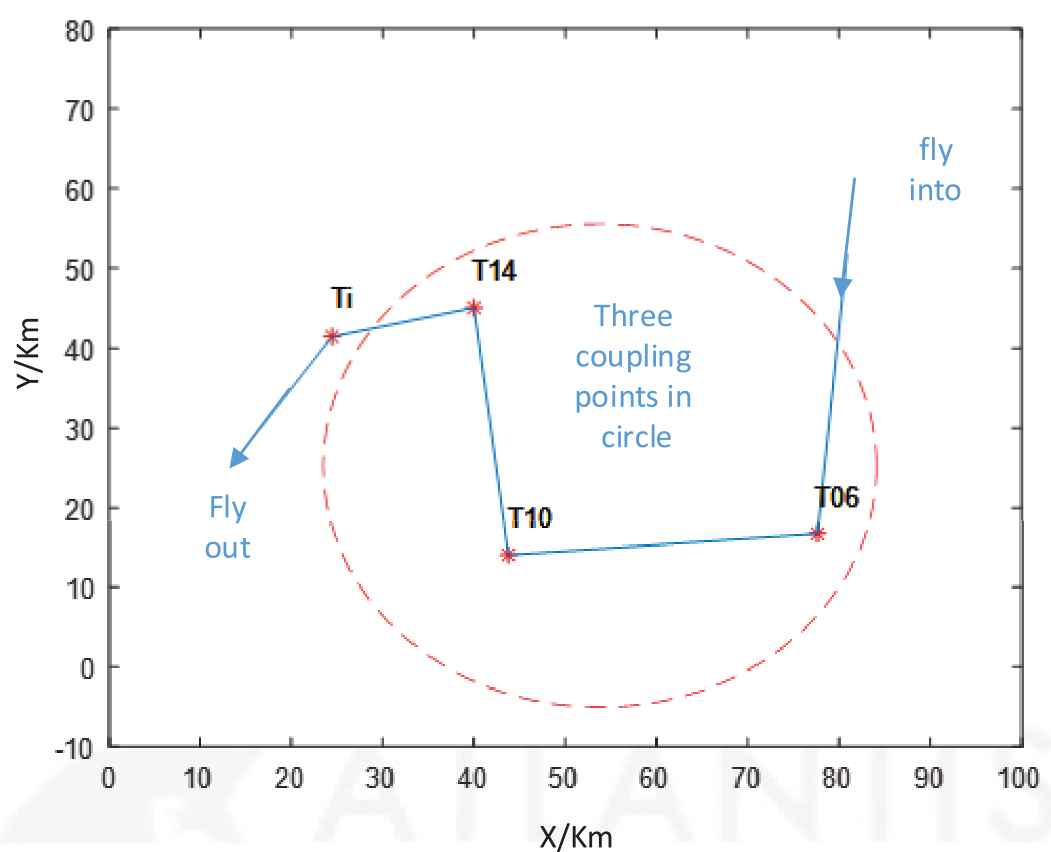
Distribution diagram of coupling points in a certain area.
2.3. Cost Function of Mission Planning
Fuel, sensors, flight speed, turning radius, acceleration, and climbing capability, as well as the environment in which the UAV is operating, which will affect the effectiveness of the UAV's performance. To facilitate calculations, the distance, variation in height, and the angle are used as evaluation indicators of the cost function. The UAV can escape the enemy's radar detection in the low active area of flight, ensuring that the UAV is flying in the absolute safety zone. The smaller altitude changes, the smaller corner, the fewer turns, and the smaller flight distance are, the better the performance the UAV have. The feasible coefficient of the planned task assignment is high, which facilitates further track smoothing and generates a flying track point. Creating an indicator function:
3. AN IACO FOR MULTI-TASK AND MULTIPLE CONSTRAINTS OF UAV
The ACO was proposed by Marco Dorigo, a famous Italian scholar, in 1991 [19]. It is a Bionic evolutionary heuristic optimization algorithm that simulates ant population foraging. It was originally used to solve the shortest path for the salesman problem and later evolved to solve the optimal problem of multi-objective combinations, asymmetric TSP, and unbalanced assignment problem. For the invisible ant, relying on the collaboration of the entire ant system, by leaving a message that can be recognized by other ants on the crawling path, the ant will explore other paths with a certain probability for the intersection without pheromones, while other ants will always follow the path of high pheromone concentration with a greater probability and then leaving new pheromones. Eventually, the shortest path from food to ant nest is formed, and the entire ant system shows a high degree of social coordination and self-organization.
3.1. Introduction to Basic ACO
The two core parts of the basic ACO are stating transfer and the updating of pheromones [20]. The option of each ant from one target point to the next in the multi-task assignment process is an important factor in determining the merits of the algorithm. The transfer probability of the
Before each iteration, it needs to empty the TS table
3.2. Introducing Human Impact Factors
In the traditional and the previous IACO, less consideration is given to the preemptive information [21]. Most of the improved methods for ACO are limited to the optimization of the transfer probability mechanism and pheromone update rule, which improves the convergence speed of the algorithm to a certain extent, and also guarantees the reliability of the algorithm to solve the optimal or suboptimal solution. In this paper, more transcendental information is studied into the design of the algorithm. The artificial influence factors, including the optimal solution of known local subsets, task sequence exclusion and coupling, will reduce the dimension of the problem and increase the solving speed of the algorithm. In the IACO, the artificial influence coefficient vector that can be used after the artificial influence factor is normalized is introduced into the distance enlightenment information in the transfer probability formula, which makes optimization time reduced and the convergence of the algorithm increased.
3.3. Normalizing the Weight Coefficient and the Artificial Influence Coefficient
In solving the problem through mathematical methods, multivariate parameter data set need to be normalized. In this paper, we use normalization
3.4. The Variable Dimension Vector Coefficient and the Time Adaptive Factor
The traditional ACO relies on roulette to select the next target point, which is highly random and has a slow convergence rate. Inspired by neural networks and in-depth learning [22], the greater probability of randomness in the initial stage of searching for food, the easier it is to find the optimal solution. After the ants find the food, the optimal or suboptimal solution will concentrate on the routing of the higher pheromone. In the early stages of the algorithm, the randomness of ants is increased like the particle swarm algorithm, thus increasing the full exploration of the entire solution space. In the middle and late stages of the algorithm, the noninferior solution space has been formed, increasing the degree of the pheromone concentration and the heuristic information, reducing the probability of exploring the segment with low pheromone concentration and small heuristic information, thus increasing the probability of solving the optimal solution [23,24]. At the same time, it also improves the computational efficiency of the improved algorithm and greatly reduces the number of iterations for the improved algorithm. The transfer probability
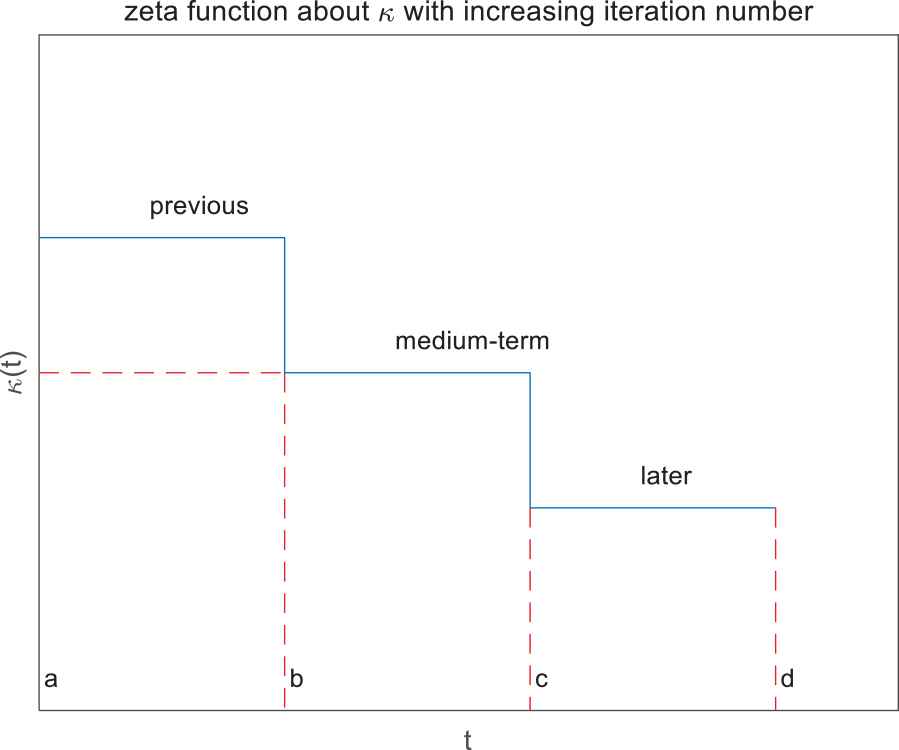
Time-dependent function diagram in variable dimension vector coefficients of transfer probability.
Where the time adaptive factor
3.5. Ant Colony Foraging Pheromones in Reality
In the actual process of ants foraging, for pheromones
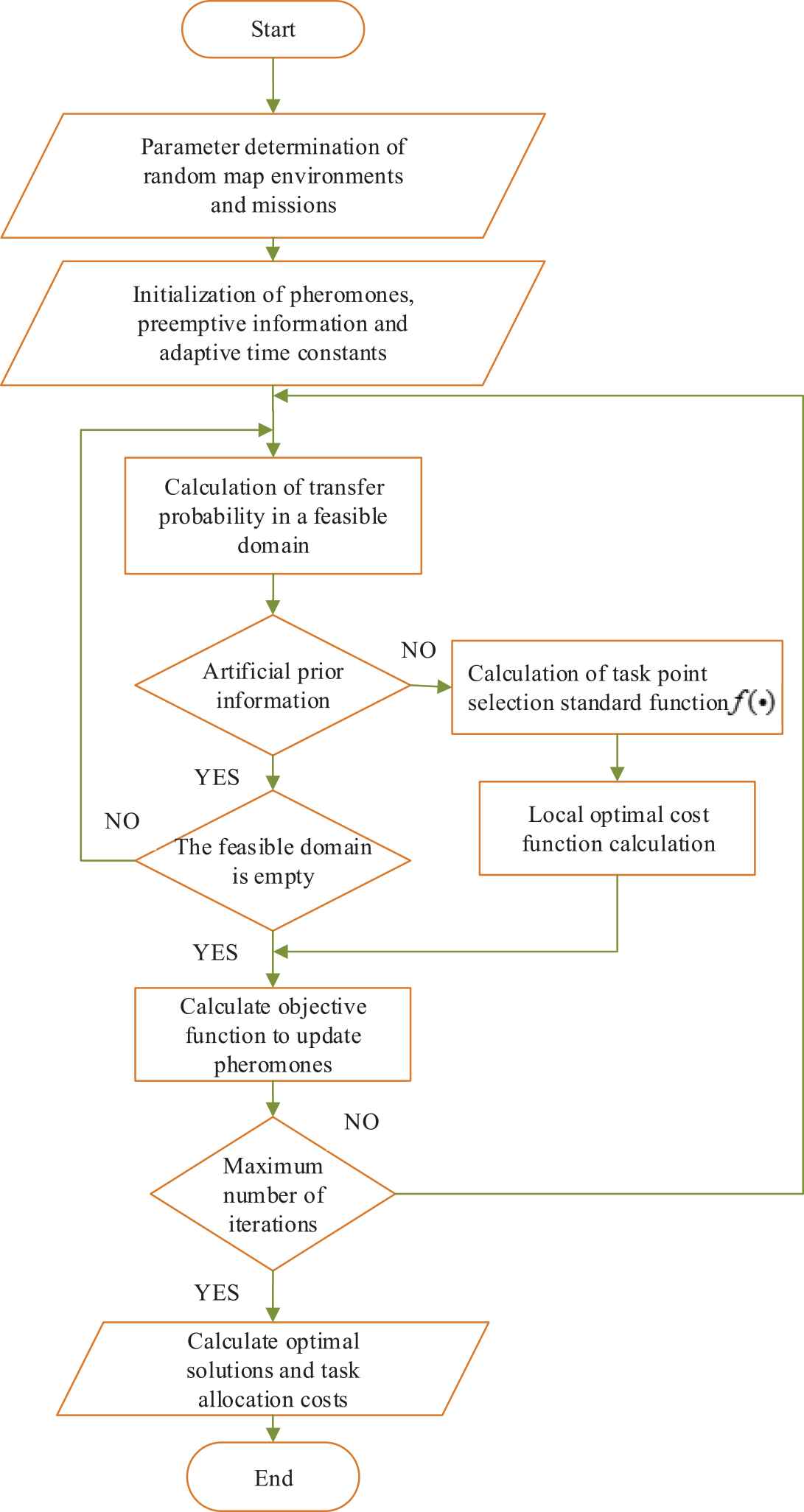
Flowchart of improved ant colony optimization.
3.6. Convergence Analysis of Improved ACO
The pheromone concentration of IACO gradually increases following ant colony transfer probability randomness in the initial stage, and the concentration of pheromones tends to stabilize in the middle stage of the algorithm, and then the concentration of pheromones continues to increase on the better path, on the contrary, the concentration of pheromones on the high-cost routes is gradually decreasing. Using the pheromone lower limit to analyze the convergence of ACO [21], when the number of cycles is
Assumption 1:
If
In any iteration, the maximum pheromone concentration of segment from
On account of
Assumption 2:
Let
In the IACOn, the initialization of pheromones is limited, and the traditional proof is difficult to continue to prove its convergence. It is known from the foregoing that each iteration has the limit of the largest amount of pheromones
In summary, for
4. SIMULATIONS AND RESULTS
In order to verify the commonality and effectiveness of the IACO, any randomly generated in a three-dimensional space with an average height of 0.8 Km, X-direction 300 Km, and Y-direction 300 Km. When the UAV executes the missions, it must maintain a certain vertical height from every target point, and the minimum value is set as 0.1 Km in this article. To form an effective comparison, randomly generated data are preserved and verified by simulation of PSO and TS algorithm. For the single simulation of ACO and PSO, the population scale is 30 and the number of iterations is 200. A total of 100 times Monte Carlo simulations are performed to find the optimal solution each time and comparison results for each iteration are shown in Figure 4.
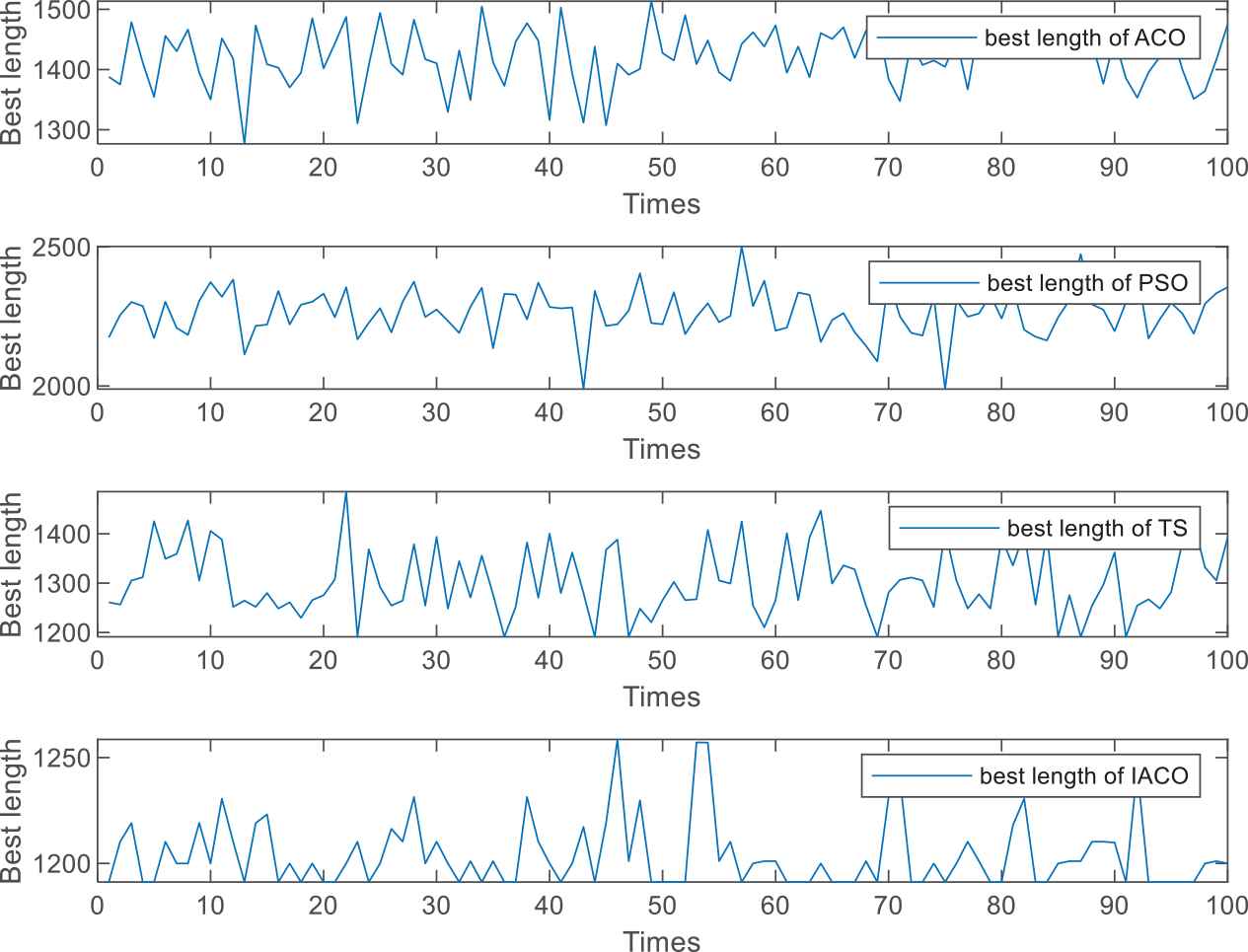
Comparison of optimal results between the improved ant colony optimization and the other three algorithms simulated 100 times.
Figures 4 and 5 show that the basic ACO, PSO, TS algorithm, and the IACO proposed in this paper can converge for iteration 200 times. In 100 times Monte Carlo simulation experiments: the final solution of the basic PSO is stable at 1400, with a fluctuation range of 100, and the algorithm takes an average time of 4.4080 seconds; the solution of the PSO is stable near 2250, with a fluctuation range of 250, and the algorithm consumes an average time of 3.8290 seconds; the final solution of the TS algorithm is stable at 1300, with the fluctuation range is 100, and the algorithm takes an average time of 2.5165 seconds; the IACO eventually stabilized at 1200 approximately, with a fluctuation range of 60, and the algorithm consumed an average time of 4.7139 seconds.
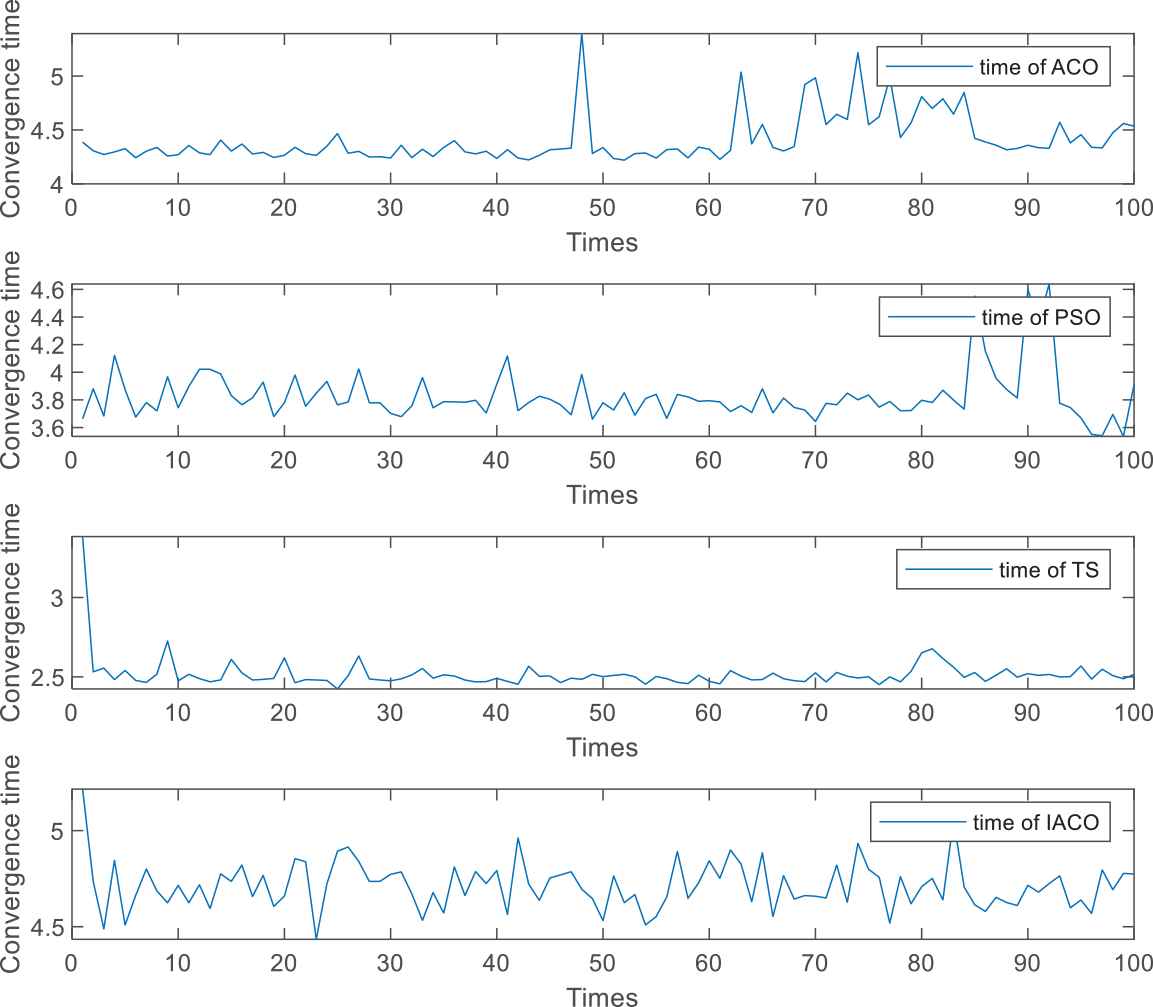
The comparison graph of convergence time between the improved ant colony optimization and the other three algorithms simulated 100 times.
From Figures 4–6, it can be seen that the four algorithms converge to the optimal or suboptimal value after 200 iterations. The basic ACO accumulates the pheromones in the process of searching and eventually converges to the optimal or suboptimal solution in the later iteration of the algorithm. When iterated to 176 times, it stabilized; PSO can solve small-scale task assignment problems, but it is easy to fall into local optimal when multi-constrained large-scale three-dimensional multi-mission planning. Although the TS algorithm can converge quickly, it is difficult to obtain an optimal solution; the IACO not only converges faster than the previous three algorithms but also converges to the optimal value only by no more than 35 iterations. Through 100 times of Monte Carlo simulations, it is confirmed that the IACO rarely falls into the local optimization, and the planned segments are feasible and easy to further track planning.
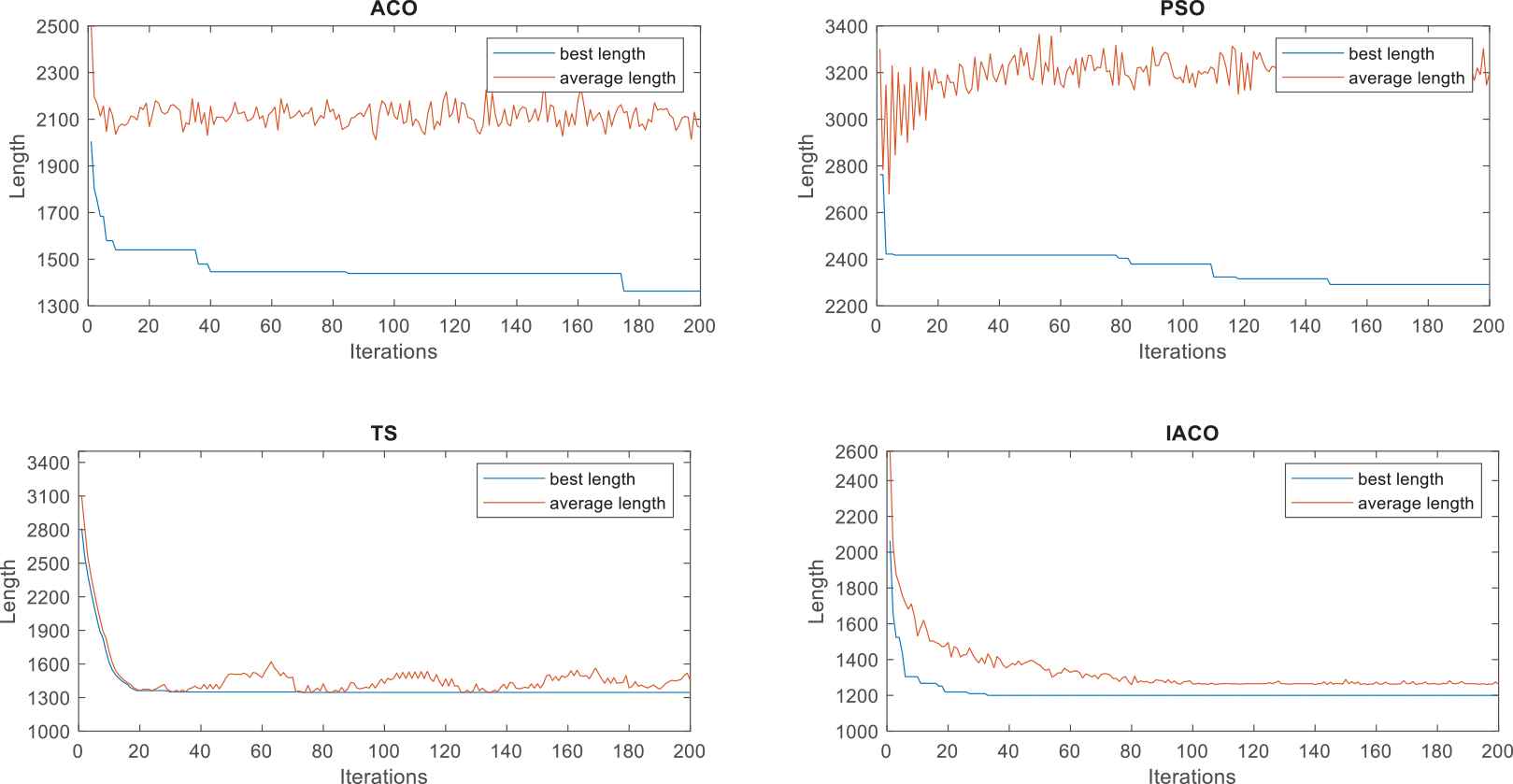
Comparison of the results of the average and optimal values of any random set in four algorithms.
In the solution the finite-time-coupling problem using IACO, the artificial preemptive information is added. Since some missions
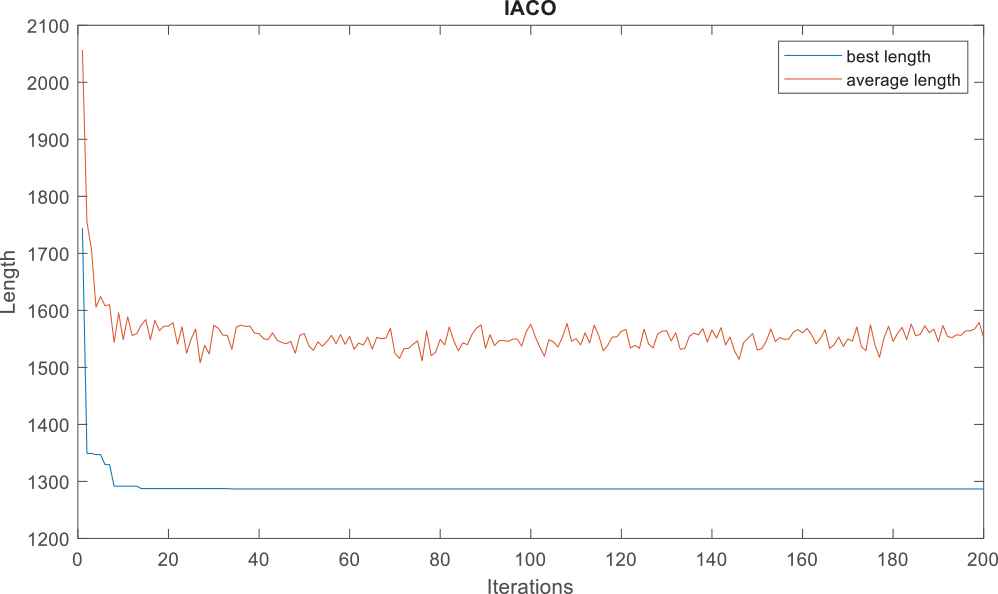
Improved ant colony optimization (IACO) solving multi-mission planning problem base on finite-time constraints.
The IACO proposed in this paper solves the three-dimensional multi-task programming problem with finite-time constraints. As Figure 8 shows, the convergence speed is fast, and the algorithm is stable and good. The optimal or suboptimal solution always appears from the final solution of each time and the average time of the IACO is 4.9344s for 100 times Monte Carlo simulation, which satisfies the requirement of fast convergence speed and feasible solution.
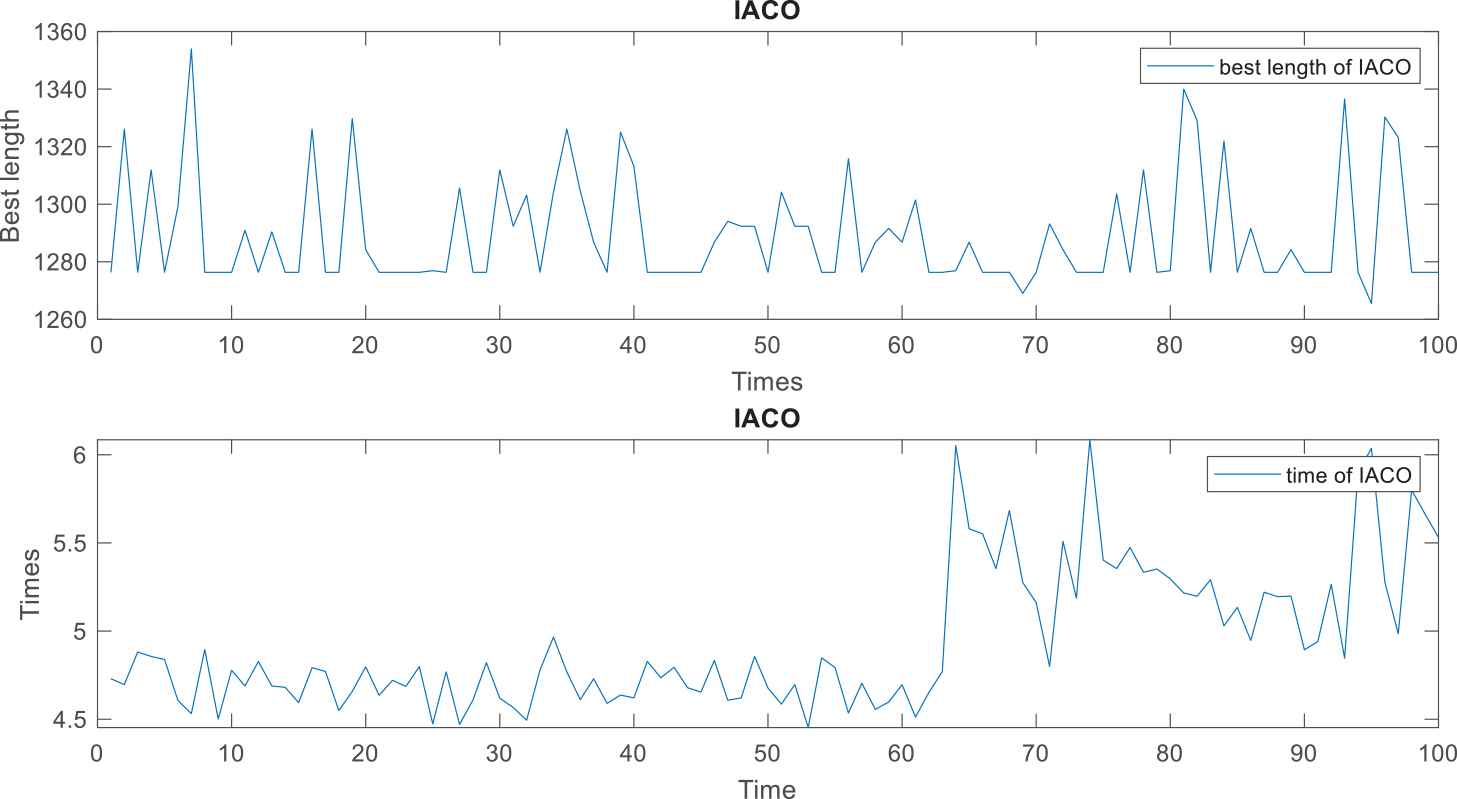
Results of improved ant colony optimization (IACO) solving time-coupling multi-mission planning for 100 times Monte Carlo simulation.
The algorithm proposed in this paper has obvious advantages in solving multi-objective optimization problems. In particular, it has a nice effect on multi-task coupled, translucent, target-time constrained problems. It is worth noting that the realization of this advantage is the utilization of prior information and artificial influencing factors. In addition, the variable dimension vector coefficient and the time adaptive factor make algorithm have strategies to search for the optimal solution, which enhances the adaptive ability of the algorithm.
5. CONCLUSION
The IACO proposed in this paper has been compared with the basic ACO, PSO, TS algorithm in detail about the convergence time and task distribution effect by 100 times Monte Carlo simulation and the advantages of IACO is fast convergence speed, good stability, and strong applicability. The IACO makes full use of more prior information and increases the intelligence and controllability of the algorithm. According to the actual foraging ways of ants, the initial pheromone is set to zero, which enlarges the random search ability of the algorithm in the entire solution space and increases the probability of the occurrence of the optimal solution or suboptimal solution. The introduction of the variable dimension vector coefficient and time adaptive factor have correlated the transfer probability with time, making the transfer probability of algorithm strategic in the former, middle, and later stage, which can guarantee the full search of the entire solution space in the previous period and it can ensure the convergence of algorithms in the middle and late, as a result, the optimal solution can be obtained. The IACO presented in this paper is effective in solving multi-constrained missions planning problems in the complex three-dimensional environment for UAV, and the algorithm is operable and practical. Through many simulations, it is proved that the IACO is stable and converges fast.
CONFLICTS OF INTEREST
The authors declare no conflict of interest.
AUTHORS' CONTRIBUTIONS
Weiheng Liu and Xin Zheng conceived and worked together to achieve this work. Weiheng Liu was responsible for investigation, conceptualization, methodology, and analysis. Xin Zheng was responsible for validation, supervision and funding acquisition. All the authors wrote, edited and revised the article.
ACKNOWLEDGMENTS
The authors are indebted to the editor and anonymous reviewers for their helpful comments and constructive suggestions. The authors wish to thank China Aerospace Science and Engineering Group for providing research facilities. This work was sponsored by Hiwing Aviation General Equipment Co., Ltd, Aerospace Science and Engineering Group.
REFERENCES
Cite this article
TY - JOUR AU - Weiheng Liu AU - Xin Zheng PY - 2020 DA - 2020/10/29 TI - Three-Dimensional Multi-Mission Planning of UAV Using Improved Ant Colony Optimization Algorithm Based on the Finite-Time Constraints JO - International Journal of Computational Intelligence Systems SP - 79 EP - 87 VL - 14 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.201021.001 DO - 10.2991/ijcis.d.201021.001 ID - Liu2020 ER -
