A Hybrid Firefly and Multi-Strategy Artificial Bee Colony Algorithm
 , Predrag S. Stanimirović2,
, Predrag S. Stanimirović2,  , Shuai Li3,
, Shuai Li3,  , Xinwei Cao4
, Xinwei Cao4- DOI
- 10.2991/ijcis.d.200612.001How to use a DOI?
- Keywords
- Firefly algorithm; Artificial bee colony; Multi-strategy; Hybrid algorithm; Global optimization
- Abstract
Many hard optimization problems have been efficiently solved by two notable swarm intelligence algorithms, artificial bee colony (ABC) and firefly algorithm (FA). In this paper, a collaborative hybrid algorithm based on firefly and multi-strategy artificial bee colony, abbreviated as FA-MABC, is proposed for solving single-objective optimization problems. In the proposed algorithm, FA investigates the search space globally to locate favorable regions of convergence. A novel multi-strategy ABC is employed to perform local search. The proposed algorithm incorporates a diversity measure to help in the switch criteria. The FA-MABC is tested on 40 benchmark functions with diverse complexities. Comparative results with the basic FA, ABC and other recent state-of-the-art metaheuristic algorithms demonstrate the competitive performance of the FA-MABC.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
There are numerous engineering and science problems which can be formulated as global optimization problems. These problems are often difficult to solve due to their diverse properties, such as nonlinearity, nondifferentiability, multi-modality and nonseparability. During last decades many metaheuristic algorithms have been proposed for solving hard optimization problems [1–5].
Two major characteristics of metaheuristics are exploitation and exploration [6]. Exploitation is the process of focusing search on a local region by using the information of previously visited good solutions. Exploration allows the algorithm to explore entirely new regions of a search space, often by randomization. Too much exploration increases the chance of finding the optimal solution with better accuracy, but usually tends to decrease the convergence speed of the algorithm [7]. On the other hand, high exploitation tends to increase the convergence rate of the algorithm, but the probability of finding global optimum may be low. Since exploitation and exploration are fundamentally conflicting processes, their balanced combination is essential for successful optimization performance.
Most metaheuristics are based on the swarm intelligence [8]. When solving an optimization problem, these algorithms use multiple interacting intelligent agents, inspired by the collective behavior of social insects, such as bees or ants. Firefly algorithm (FA) [9] and artificial bee colony (ABC) [10] are two widely used swarm intelligence algorithms originally proposed to solve numerical optimization problems. Both algorithms have simple concepts and easy implementation. The main difference between the FA and ABC is how new solutions are created and then used at each iteration. Earlier studies indicate that the FA has good exploration and exploitation abilities, but it may suffer from high computational complexity and it may show slow convergence speed during the search process [11,12]. On the other hand, the solution search equation of ABC algorithm is good for exploration [13], while the selection mechanism guides the search toward regions of the best solutions. However, solution quality does not improve sufficiently fast when the ABC is applied to solve some complex problems [14].
According to the no free lunch theorem [15], no single algorithm is suitable for solving all optimization problems. Consequently, it is important to know which algorithm performs best on which type of optimization problems. Therefore, original variants of metaheuristics are later modified to improve their performances. The main enhancements are reached by the adaptation of parameters, by modifications of solution search equations and creation of ensemble method which combines multiple search strategies [13,16,17]. Besides these improvements, there are also hybrid algorithms which have a prominent role in enhancing the search capability of algorithms.
In a hybrid algorithm, two or more algorithms are cooperatively solving an optimization problem [18]. The aim of hybridization is to combine the benefits of each algorithm, while at the same time it tries to minimize any considerable disadvantage. As a result, hybrid algorithm can achieve better performance than a single algorithm in terms of either computational speed or accuracy. Since various algorithms have their own characteristics which are suitable for different problems, there are a lot of studies that hybridize different metaheuristics in order to produce a valuable synergy from their combination. Recent studies indicate that hybrid approaches are effective for global optimization [19,20].
Motivated by these research studies, in this paper a novel hybrid method based on FA and multi-strategy artificial bee colony (MABC) is proposed to solve complex numerical optimization problems. The proposed hybrid algorithm, abbreviated as FA-MABC, belongs to the category of collaborative hybrids with multi-stage structure [18]. There are two stages in this case. To take advantage of the good search abilities of the FA, it is used in the first stage with the intention to find promising areas of the search space. In order to reduce computational complexity of the FA, the FA variant in which each solution in each iteration can be updated at most once is employed. Output of the FA is then supplied as the input to a novel multi-strategy ABC, which performs a local search. In the proposed MABC two distinct search strategies coexist throughout the search process and participate in creating candidate solutions. The use of the two search strategies which have different advantages so that they support each other during the search and the selection mechanism, enables the proposed algorithm to efficiently investigate the neighborhood of good solutions. Finally, a diversity measure is used in order to determine when to switch from the FA to the MABC.
To evaluate the performance of FA-MABC, it is tested on 12 well-known benchmark functions and on a set of 28 benchmark instances taken from CEC2013 competition. The obtained results are compared to those of the basic FA, ABC and their recent variants, as well as two other successful metaheuristic approaches.
Rest of this paper is organized as follows: The basic FA and ABC are presented in Section 2. Section 3 describes the new approach FA-ABC in detail. The experimental results and the corresponding analysis are presented in Section 4. Section 5 provides concluding remarks.
2. A BRIEF INTRODUCTION OF FA AND ABC
2.1. Firefly Algorithm
The FA, developed by Yang, is a population-based metaheuristics inspired by communication behavior of flashing fireflies [8]. Its mathematical model is proposed according to the following idealized characteristics of the flashing fireflies [21]: (1) all fireflies are unisex, (2) a firefly’s attractiveness is proportional to its light intensity or brightness and (3) a firefly’s brightness is determined by the landscape of the fitness function.
In the population of fireflies, each firefly represents a candidate solution in the search space. The attractiveness between fireflies can be defined by monotonically decreasing function [8]:
If the objective function value of
Later findings indicate the solution quality can be improved by reducing the randomization parameter
The pseudo code of the basic FA is described in Algorithm 1. The input of Algorithm 1 includes the population size value
2.2. Artificial Bee Colony
ABC algorithm is a metaheuristic technique inspired by the foraging behavior of natural honey bee swarms [10]. In the ABC a colony of artificial bees consists of three groups of bees: employed bees, onlooker bees and scouts. One half of the population of artificial bees are employed bees, while the other half consists of the onlookers and scouts. The number of the employed bees is equal to the number of food sources (possible solutions). Employed bees are all bees that are currently exploiting a food source, meanwhile they share their information about food sources with the onlookers. Onlooker bees select quality food sources from those found by the employed bees and further search the foods around the selected food sources. Employed bees that abandon their unpromising food sources to search for new ones become scout bees.
Algorithm 1 Pseudo-code of the basic FA
Create initial population of solutions
Calculate the objective function value of each solution;
while
for
for
if
Move
Calculate the objective function value of the new
end if
end for
end for
Rank the fireflies and find the current best;
end while
In the initialization step of the ABC algorithm, the population of solutions is created randomly in the search space. After the initialization step, the employed, onlooker and scout phases are repeated a predefined number of generations. In the end of each generation, the found source so far is memorized.
In the employed phase every solution
In the onlooker phase, the solutions which will be subjected to the update process are selected according to the fitness proportionate selection. The update process in the onlooker phase is the same as in the employed phase. In the scout phase, solutions that do not change over a certain number of trials are again initialized.
2.3. FA and ABC Variants
Nowadays the FA and ABC represent some of the most popular metaheuristic algorithms due to their effective performance and easy implementation.
Several prominent FA variants were proposed for solving continuous optimization problems. Novel chaotic improved firefly algorithm (CFA) was presented in Ref. [22]. Different chaotic maps are used to replace the attraction parametes
Although the basic FA was originally developed for solving continuous optimization problems, the extended versions have been also described for the discrete and combinatorial types of problems. Some of these versions were applied to solve scheduling problems, queueing system and traveling salesman problems [21].
There are numerous ABC variants for solving numerical optimization problems. For instance, in Ref. [14] it was noticed that the ABC algorithm needs more parameters to be mutated in the parent solution in order to improve convergence speed. Hence, the ABC search strategy used a novel control parameter that determines how many parameters should be modified for the production of a neighboring solution. Multi-strategy ensemble ABC (MEABC) algorithm is ABC variant in which a pool of distinct solution search strategies coexists throughout the search process and competes to create candidate solutions [13]. A novel ABC algorithm with local and global information interaction (ABCLGII) is a recent ABC variant which proposes two information interaction mechanisms for employed and onlooker bees [25]. The ABC based on the gravity model (ABCG) is a newly proposed variant of ABC which employs an attractive force model for choosing a better neighbor of a current solution to enhance the exploitation ability of ABC [26]. A novel individual-dependent multi-colony ABC algorithm (IDABC) is a recent ABC variant, in which the whole colony is divided into three sub-colonies and three evolution operators are introduced into the corresponding sub-colonies in order to play different roles [27]. An improved ABC based on the multi-strategy fusion (MFABC) is one of the latest ABC variants proposed in Ref. [28] to enhance the search ability of ABC with small population.
Apart from ABC variants for numerical optimization problems, the extended ABC versions also have been described for the discrete and combinatorial types of problems. Some of these versions were applied to solve capacitated vehicle routing problem, the reliability redundancy allocation problem, different versions of scheduling problem, economic load dispatch problem and knapsack problem. Application areas of ABC algorithm include neural networks, image processing, data mining, industrial, mechanical, electrical, electronics, control, civil and software engineering [29].
3. THE PROPOSED APPROACH: FA-MABC
The randomization term of the FA search equation gives an ability to the algorithm to escape from a local optimum in order to search on a global level. In terms of the attraction mechanism, individuals can subdivide themselves into several subgroups, and each group can seek around a local region [30]. These characteristics point out that the FA has good exploration and exploitation abilities. Although the FA has gotten success in different areas, it has some insufficiencies. In the FA the solutions are still changing as the optima are approaching, which may slow down the convergence speed [9]. In addition, the search process of the FA has high computational complexity since each firefly is attracted by all other brighter fireflies in the swarm.
On the other hand, the ABC search strategy has good exploration ability. Thus ABC is very efficient in solving multimodal and multidimensional basic functions. However, the convergence rate of the ABC is slow when it is applied to solve hybrid complex problems. To successfully solve these problems, the ABC solution search equation needs to be modified [14].
Since the FA and ABC have their own positive features, their combination could produce a valuable synergy. Therefore, a collaborative hybrid algorithm based on firefly and ABC is developed. The FA explores the search space globally to locate the favorable regions of the search space, whereas the novel version of ABC algorithm performs local search. Inspired by earlier mentioned observations related to ABC, we propose a novel multi-strategy ABC to act as the local searcher. In addition, the diversity measure is used to help in the switch criteria. Therefore the proposed FA-MABC has three main components, the global search optimizer, the local search algorithm and the switch criteria. The details of each component and implementation steps of the FA-MABC are presented as follows.
3.1. The Global Search Optimizer
In the proposed hybrid algorithm, the global searcher is the variant of FA which uses random attraction model. In this FA variant each solution is compared to another randomly selected solution from the set of promising solutions in the population. Assume that all
In the basic FA, the average number of updates of solution in each generation is
3.2. The Local Search Algorithm
ABC performance mainly depends on its search equation given by Eq. (5). According to the Eq. (5), the new candidate solution is created by moving the old solution to a randomly selected individual, and the search direction is completely random. Hence the Eq. (5) is random enough for exploration and consequently can provide solutions with plenty of diversity and far from the actual solutions.
Diverse optimization problems require different search strategies depending on the characteristics of problems. It was noticed that the ABC needs to mutate more parameters in the neighborhood of the current solution to successfully solve hybrid complex problems, while the use of standard search strategy given by the Eq. (5) can efficiently solve basic functions [14]. Therefore, the number of parameters in the parent solution which are modified in the update process is very important.
Combining search strategies which have different abilities so that they can complement each other during the search process can achieve better optimization results than a single search strategy as in the basic ABC [13]. Motivated by these findings, an ensemble of multiple solution search strategies for ABC (MABC) is developed to perform local search. In the proposed MABC, two search equations coexist throughout the search process and compete to create better new solutions. The first one is basic ABC search strategy given by Eq. (5). The second search strategy employed in the MABC in order to generate a new candidate solution
It is expected that the basic ABC search equation given by Eq. (5) provides good exploration ability but slower convergence speed, while the employed search strategy of the MABC given by Eq. (8) shows the fast convergence rate.
Algorithm 2 Dynamic regulation for search strategy
if
{solution
else
if
else
end if
{solution
end if
In order to determine how to assign these search strategies to solutions from the population, an encoding method is used. This encoding method is inspired by the study given in Ref. [13]. Let us denote the search strategy given by the Eq. (5) as
This encoding method is presented in Algorithm 2. The input of Algorithm 2 includes the parent solution
3.3. The Switch Criteria
Differences among individuals of a population are prerequisite for exploration, but too much diversity in each phase of the search, may lead to inefficient search. Population diversity is usually high at the beginning of a search process, and it decreases as the population moves towards the global optimum.
In the implementation of the FA-MABC it is important to know when to switch from the FA to MABC. For this purpose the FA-MABC incorporates the diversity metric as Eq. (9) to measure the population diversity [25].
Variable
3.4. The Pseudo-Code of the FA-MABC
The FA-MABC uses the boundary constraint handling mechanism which ensures that if variables of a created solution by each of these three search equations go outside of boundaries, a diverse set of values is created. This boundary constraint handling method is given by [16]
Algorithm 3 Pseudo-code of the FA-MABC
Create initial population of solutions
Randomly initialize
Calculate the population diversity
while
if (
for
Randomly select solution
if
Move
Apply control of the boundary conditions on the created solution by Eq. (10) and evaluate it;
end if
end for
Rank the solutions;
Calculate the population diversity
if (
end if
else
for
Produce new solution
Apply control of the boundary conditions on the created solution
Update
end for
end if
Find the current best solution;
end while
The pseudo-code of the FA-MABC is described in Algorithm 3. The input of Algorithm 3 includes the population size value
To solve a particular problem
4. EXPERIMENTAL STUDY
To investigate the performance of the FA-MABC, 12 well-known scalable benchmark functions with 30 and 100 variables and a set of 28 benchmarks taken from CEC2013 competition are used. The brief descriptions of the 12 well-known benchmark functions are listed in Table 1. When the objective function value of the best solution obtained by an algorithm in a run is less than the corresponding acceptable value, the run is regarded as a successful run. Presented benchmark functions can be divided into two categories according to their features: unimodal functions (
| Function | Name | Search Range | Min. | Accept |
|---|---|---|---|---|
| Sphera | 0 | 1e-8 | ||
| Schwefel 2.22 | 0 | 1e-8 | ||
| Schwefel 2.21 | 0 | 1e+0 | ||
| Step | 0 | 1e-8 | ||
| Quartic | 0 | 1e-1 | ||
| Rosenbrock | 0 | 1e-1 | ||
| Rastrigin | 0 | 1e-8 | ||
| Griewank | 0 | 1e-8 | ||
| Schwefel2.26 | 0 | 1e-8 | ||
| Ackeley | 0 | 1e-8 | ||
| Penalized1 | 0 | 1e-8 | ||
| Penalized2 | 0 | 1e-8 |
Benchmark functions used in the experiments, where D is the problem dimension.
In order to evaluate the performance of the FA-MABC, it is compared to the basic FA, ABC and recent variants of the FA and ABC. In these experiments two types of comparisons were examined. First type of comparison is a direct comparison, where the basic FA, ABC and FA-MABC were implemented and their corresponding performances are investigated. In the second type of comparison, the results of other prominent variants of FA and ABC were taken from the specialized literature and compared with those achieved by FA-MABC. The last experiment is used to discuss how the proposed algorithmic components affect the performance of FA-MABC.
4.1. Comparison with the Basic FA and ABC
In this subsection, the FA-MABC is compared with the basic FA and ABC on 12 scalable benchmark functions listed in Table 1 with 30 and 100 variables. Each algorithm was implemented in Java programming language on a PC with Intel(R) Core(TM) i5-4460 3.2GHz processor with 16GB of RAM and Windows OS.
In the proposed FA-MABC, values of the parameter
In the FA and ABC, the
The mean and corresponding standard deviation values of 30 independent runs are used to determine the quality or accuracy of the solutions achieved by the FA, ABC and FA-MABC. The convergence speed of each approach is compared by the metric AVEN. This metric records the average number of function evaluations needed to reach the acceptable value, which is used to evaluate the convergence speed. The robustness or reliability of each algorithm is compared by measuring the success rate (SR%). This rate denotes the ratio of successful runs in the 30 independent runs. The convergence speed is faster if the value of AVEN is smaller, while the robustness of an algorithm is better if the value of SR is greater. Wilcoxon’s rank sum test at a 0.05 significance level was applied between the compared metaheuristic algorithm and the FA-MABC. The result of the test is presented as +/=/-, which means that the corresponding algorithm is significantly better than, statistically similar to, and significantly worse than the FA-MABC.
The statistical results of the comparisons on the benchmarks with 30 and 100 dimensions are summarized in Tables 2 and 3. These results include the obtained mean best function values and corresponding standard deviations, AVEN and SR results. The best results are indicated in bold.
| Fun. | Metric | FA | ABC | FA-MABC |
|---|---|---|---|---|
| Mean(std.) | 6.28e-05(1.02e-05)- | 4.95e-16(7.47e-17)- | 3.97e-286(0.00e+00) | |
| AVEN(SR) | NaN(0) | 32233(100) | 6133(100) | |
| Mean(std.) | 3.76e-03(3.77e-04)- | 1.30e-15(1.35e-16)- | 2.36e-152(8.26e-152) | |
| AVEN(SR) | NaN(0) | 48287(100) | 9415(100) | |
| Mean(std.) | 3.79e-03(5.81e-04)- | 7.56e-01(4.61e-01)- | 2.53e-97(1.36e-96) | |
| AVEN(SR) | 35983(100) | 123820(80) | 652(100) | |
| Mean(std.) | 1.67e-01(5.82e-01)- | 0.00e+00(0.00e+00)= | 0.00e+00(0.00e+00) | |
| AVEN(SR) | NaN(0) | 9582(100) | 1009(100) | |
| Mean(std.) | 7.08e-02(1.74e-02)- | 4.96e-02(9.05e-03)- | 5.50e-04(2.55e-04) | |
| AVEN(SR) | 16055(97) | 45506(100) | 223(100) | |
| Mean(std.) | 3.74e+01(2.84e+01)- | 1.93e-01(4.71e-01)- | 8.80e-30(2.52e-29) | |
| AVEN(SR) | NaN(0) | 69257(77) | 1984(100) | |
| Mean(std.) | 4.15e+01(9.22e+00)- | 0.00e+00(0.00e+00)= | 0.00e+00(0.00e+00) | |
| AVEN(SR) | NaN(0) | 50031(100) | 6760(100) | |
| Mean(std.) | 4.67e-03(5.05e-03)- | 9.03e-04(3.73e-03)- | 0.00e+00(0.00e+00) | |
| AVEN(SR) | NaN(0) | 43382(93) | 6291(100) | |
| Mean(std.) | 5.23e+03(7.00e+02)- | 1.57e-12(2.14e-12)- | 0.00e+00(0.00e+00) | |
| AVEN(SR) | NaN(0) | 71002(100) | 6918(100) | |
| Mean(std.) | 1.93e-03(1.16e-04)- | 3.86e-14(4.76e-15-) | 3.64e-15(1.07E-15) | |
| AVEN(SR) | NaN(0) | 55905(100) | 9192(100) | |
| Mean(std.) | 3.46e-03(1.86e-02)- | 5.11e-16(7.01e-17)- | 1.57e-32(5.47e-48) | |
| AVEN(SR) | NaN(0) | 28153(100) | 5568(100) | |
| Mean(std.) | 3.70e-03(6.60e-03)- | 4.48e-16(9.65e-17)- | 1.35e-31(6.57e-47) | |
| AVEN(SR) | NaN(0) | 39590(100) | 9029(100) | |
| +/=/- | 0/0/12 | 0/2/10 | - | |
FA, firefly algorithm; ABC, artificial bee colony; FA-MABC, firefly and multi-strategy artificial bee colony; SR, success rate.
Comparison results of the FA, ABC and FA-MABC on 12 benchmark functions with 30D. The best results are indicated in bold.
| Fun. | Metric | FA | ABC | FA-MABC |
|---|---|---|---|---|
| Mean(std.) | 7.27e-04(7.56e-5)- | 2.18e-15(1.71e-16)- | 0.00e+00(0.00e+00) | |
| AVEN(SR) | NaN(0) | 112177(100) | 12911(100) | |
| Mean(std.) | 2.87e-02(5.24e-03)- | 5.03e-15(2.29e-16)- | 7.25e-226(0.00e+00) | |
| AVEN(SR) | NaN(0) | 171409(100) | 21435(100) | |
| Mean(std.) | 5.22e-02(1.69e-02)- | 2.31+01(2.93+00)- | 5.71e-07(1.62e-06) | |
| AVEN(SR) | 262971(100) | NaN(0) | 707(100) | |
| Mean(std.) | 1.40e+00(16.70e+00)- | 0.00e+00(0.00e+00)= | 0.00e+00(0.00e+00) | |
| AVEN(SR) | NaN(0) | 35593(100) | 995(100) | |
| Mean(std.) | 3.70e-01(5.24e-02)- | 1.58e-01(2.06e-02)- | 5.71e-04(1.85e-04) | |
| AVEN(SR) | NaN(0) | -(0) | 454(100) | |
| Mean(std.) | 1.30e+02(9.42e+01)- | 6.18e-01(1.20e-01)- | 8.46e-30(2.48e-29) | |
| AVEN(SR) | NaN(0) | 280551(47) | 2133(100) | |
| Mean(std.) | 2.30e+02(2.86+01)- | 0.00e+00(0.00e+00)= | 0.00e+00(0.00e+00) | |
| AVEN(SR) | NaN(0) | 187870(100) | 12718(100) | |
| Mean(std.) | 1.27e-03(2.19e-03)- | 5.45e-15(2.70e-14)- | 0.00e+00(0.00e+00) | |
| AVEN(SR) | NaN(0) | 124554(100) | 16061(100) | |
| Mean(std.) | 2.87e-02(5.24e-03)- | 1.18e-10(2.96e-11)- | 1.09e-10(0.00e+00) | |
| AVEN(SR) | NaN(0) | 331965(100) | 11844(100) | |
| Mean(std.) | 3.48e-03(1.58e-04)- | 1.52e-13(1.10e-14)- | 8.55e-15(3.26e-15) | |
| AVEN(SR) | NaN(0) | 191609(100) | 19556(100) | |
| Mean(std.) | 2.07e-03(7.76e-03)- | 2.183e-15(6.04e-16)- | 4.71e-33(1.37e-48) | |
| AVEN(SR) | NaN(0) | 143832(100) | 10058(100) | |
| Mean(std.) | 2.52e-02(3.55e-02)- | 2.13e-15(1.56e-16)- | 1.35e-31(6.57e-47) | |
| AVEN(SR) | NaN(0) | 96054(100) | 23399(100) | |
| +/=/- | 0/0/12 | 0/2/10 | - | |
FA, firefly algorithm; ABC, artificial bee colony; FA-MABC, firefly and multi-strategy artificial bee colony; SR, success rate.
Comparison results of the FA, ABC and FA-MABC on 12 benchmark functions with 100D. The best results are indicated in bold.
Results from Tables 2 and 3 clearly show that the FA-MABC is significantly better than the basic ABC and FA on all test functions in terms of solution accuracy, robustness and convergence rate. Exceptions are problems
4.2. Comparison with the Other Variants of FA and ABC
In this subsection, the FA-MABC is compared with six recent FA and ABC variants, i.e., RaFA [11], NaFA [12], ICFA [24], ABCLGII [25], ABCG [26] and MFABC [28] on 12 test functions with 30 variables. These 12 approaches were previously tested to solve same benchmarks and had a very good results.
Results reported by other FA and ABC variants were taken from the specialized literature and compared with those achieved by the FA-MABC. The results obtained by the RaFA and NaFA are taken from Ref. [12], while the results reached by the ICFA is taken from Ref. [24]. The results of ABCLGII are taken from Ref. [25], the results of the ABCG are taken from Ref. [26], while the results of the MFABC are taken from Ref. [28]. In the RaFA and NaFA, the value of
To check for statistically significant differences between the FA-MABC and each compared algorithm for all benchmark functions, the multiproblem Wilcoxon signed-rank test at a 0.05 significance level is conducted [33]. The results of this test are represented as “+/=/−,, “
The mean best results and the statistical results of applying Wilcoxons test between the FA-MABC and each FA and ABC variant are listed in Table 4 for 12 problems with 30 variables. Best mean results are indicated in bold.
| Fun. | RaFA | NaFA | ICFA | ABCLGII | ABCG | MFABC | FA-MABC |
|---|---|---|---|---|---|---|---|
| Mean | Mean | Mean | Mean | Mean | Mean | Mean | |
| 5.36e-184 | 4.43e-29 | 1.24e-39 | 3.48e-89 | 3.67e-109 | 2.46e-123 | 3.97e-286 | |
| 8.76e-05 | 2.98e-15 | 1.54e-20 | 2.13e-46 | 6.93e-062 | 7.17e-64 | 2.36e-152 | |
| 2.43e+00 | 3.43e-15 | 1.67e-20 | 1.14e-04 | 2.03e-026 | 1.81e-02 | 2.53e-97 | |
| 0.00e+00 | 0.00e+00 | 0.00e+00 | 0.00e+00 | 0 | 0 | 0.00e+00 | |
| 5.47e-02 | 2.91e-02 | 1.90e-04 | 1.44e-02 | 2.70e-03 | 1.41e-02 | 5.50e-04 | |
| 2.92e+01 | 2.39e+01 | 2.53e-05 | 4.83e+00 | 5.39e+01 | 2.47e-01 | 8.80e-30 | |
| 2.69e+01 | 2.09e+01 | 5.92e-17 | 0.00e+00 | 0 | 0 | 0.00e+00 | |
| 0.00e+00 | 0.00e+00 | 3.70e-18 | 1.28e-03 | 0 | 0 | 0.00e+00 | |
| 5.03e+02 | 6.86e+03 | 3.82e-04 | 3.57e-12 | 0 | 1.82e-13 | 0.00e+00 | |
| 3.61e-14 | 3.02e-14 | 2.60e-14 | 8.95e-15 | 4.44e-15 | 1.68e-14 | 3.64e-15 | |
| 4.50e-05 | 1.36e-31 | 1.57e-32 | 1.57e-32 | 1.57e-032 | 1.57e-032 | 1.57e-32 | |
| 8.25e-32 | 2.13e-30 | 1.42e-31 | 1.50e-33 | 1.35e-032 | 1.35e-032 | 1.35e-31 | |
| 53/2 | 55/0 | 37/8 | 42/3 | 25/3 | 33/3 | - | |
| 0.009 | 0.005 | 0.086 | 0.021 | 0.063 | 0.036 | - | |
RaFA, FA with random attraction; NaFA, FA with neighborhood attraction; ICFA, improved chaotic FA; ABCLGII, ABC algorithm with local and global information interaction; ABCG, ABC based on the gravity model; MFABC, ABC based on the multi-strategy fusion; FA-MABC, firefly and multi-strategy artificial bee colony.
Comparison results of the RaFA, NaFA, ICFA, ABCLGII, ABCG, MFABC and FA-MABC on 12 benchmark functions with 30D D. The best mean results are indicated in bold.
As shown in Table 4, the FA-MABC outperforms or performs similarly to its competitors in most cases. Precisely, the FA-MABC is better than the RaFA, NaFA, ICFA, ABCLGII, ABCG and MFABC on 9, 10, 9, 8, 6 and 7 cases respectively. In contrast, the FA-MABC is outperformed by the RaFA, NaFA, ICFA, ABCLGII, ABCG and MFABC on 1, 0, 1, 1, 1, 1 benchmarks respectively. With respect to the best results reached by all compared metaheuristics, the FA-MABC performs the best, and achieves the best results on 10 instances for these benchmarks. The second best approach is the ABCG, which performs the best on 5 test problems. From the results of Wilcoxon test presented in Tables 4 and 5, it can be seen that the FA-MABC obtains higher
| Fun. | MPEDE | HCLPSO | FADMF | FADCG | IDABC | ABCG | FA-MABC |
|---|---|---|---|---|---|---|---|
| Mean err. | Mean err. | Mean err. | Mean err. | Mean err. | Mean err. | Mean err. | |
| 0.000e+0 | 3.695e-13 | 5.61e-4 | 1.06e-3 | 0.000e+0 | 6.537e-13 | 2.274e-13 | |
| 1.271e+4 | 1.036e+6 | 3.96e+6 | 6.59e+6 | 1.069e+4 | 1.092e+7 | 9.965e-01 | |
| 4.370e+4 | 4.748e+7 | 9.14e+6 | 1.19e+7 | 2.686e+3 | 6.250e+8 | 8.771e+03 | |
| 1.383e-4 | 1.969e+3 | 1.38e+5 | 2.57e+5 | 9.680e-6 | 7.686e+4 | 5.402+00 | |
| 1.137e-13 | 4.832e-13 | 1.92e-2 | 1.78e-1 | 1.137e-13 | 5.400e-13 | 3.411e-13 | |
| 6.679e-13 | 1.796e+1 | 2.65e+1 | 2.73e+1 | 2.274e-13 | 4.160e+1 | 3.542e-08 | |
| 1.528e+1 | 1.704e+1 | 4.98e+0 | 6.35e+0 | 1.703e+1 | 9.944e+1 | 1.056e-01 | |
| 2.095e+1 | 2.096e+1 | 2.14e+1 | 2.14e+1 | 2.093e+1 | 2.093e+1 | 1.124e-01 | |
| 1.990e+1 | 1.716e+1 | 1.01e+1 | 8.74e+0 | 1.822e+1 | 2.913e+1 | 7.448e-01 | |
| 3.911e-2 | 1.935e-1 | 1.95e-1 | 5.50e-1 | 4.678e-2 | 2.635e-1 | 9.865e-03 | |
| 0.000e+0 | 1.812e-10 | 3.88e+1 | 2.42e+1 | 7.105e-15 | 1.492e-13 | 5.684e-14 | |
| 2.823e+1 | 5.261e+1 | 3.77e+1 | 2.96e+1 | 1.487e+1 | 1.307e+2 | 9.865e-03 | |
| 6.903e+1 | 1.282e+2 | 9.43e+1 | 7.85e+2 | 2.925e+1 | 2.065e+2 | 2.842e-13 | |
| 5.079e-1 | 1.392e+1 | 2.20e+2 | 1.51e+3 | 2.030e-1 | 2.504e-1 | 1.748e-12 | |
| 3.462e+3 | 3.598e+3 | 2.23e+3 | 2.52e+3 | 3.393e+3 | 3.816e+3 | 8.463e-11 | |
| 2.396e+0 | 1.618e+0 | 1.29e-1 | 3.30e-1 | 5.884e-3 | 1.653e+0 | 2.461e-01 | |
| 3.044e+1 | 3.504e+1 | 8.71e+1 | 7.59e+1 | 3.044e+1 | 3.044e+1 | 1.430e-03 | |
| 6.095e+1 | 8.244e+1 | 9.16e+1 | 8.61e+1 | 5.234e+1 | 2.101e+2 | 0.000e+00 | |
| 1.299e+0 | 1.434e+0 | 4.01e+0 | 3.47e+0 | 1.127e+0 | 6.914e-1 | 3.411e-13 | |
| 1.054e+1 | 1.003e+1 | NA | NA | 1.047e+1 | 1.437e+1 | 1.137e-13 | |
| 3.054e+2 | 2.607e+2 | 3.39e+2 | 3.12e+2 | 3.593e+2 | 2.375e+2 | 1.364e-12 | |
| 7.861e+1 | 1.359e+2 | 2.61e+3 | 1.71e+3 | 8.839e+1 | 2.327e+1 | 1.023e-12 | |
| 3.515e+3 | 3.787e+3 | 3.31e+3 | 2.99e+3 | 3.561e+3 | 5.095e+3 | 9.095e-13 | |
| 2.426e+2 | 2.247e+2 | 2.22e+2 | 2.23e+2 | 2.402e+2 | 2.807e+2 | 9.095e-13 | |
| 2.530e+2 | 2.584e+2 | 2.32e+2 | 2.25e+2 | 2.616e+2 | 2.959e+2 | 6.150e-13 | |
| 2.000e+2 | 2.001e+2 | 2.85e+2 | 3.00e+2 | 2.000e+2 | 2.009e+2 | 2.501e-12 | |
| 7.491e+2 | 5.371e+2 | 5.17e+2 | 4.85e+2 | 6.783e+2 | 7.925e+2 | 2.274e-13 | |
| 4.356e+2 | 3.000e+2 | 3.09e+2 | 2.97e+2 | 2.750e+2 | 3.000e+2 | 2.274e-12 | |
| 387/19 | 406/0 | 375/3 | 378/0 | 353/53 | 406/0 | - | |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | - | |
MPEDE, multi-population ensemble DE; HCLPSO, heterogeneous comprehensive learning PSO; IDABC, individual dependent multi-colony ABC algorithm; ABCG, ABC based on the gravity model; FA-MABC, firefly and multi-strategy artificial bee colony.
Comparison results of the MPEDE, HCLPSO, FADMF, FADCG, IDABC, ABCG and FA-MABC on CEC2013 benchmark functions with 30D D. NA means not available. The best mean of the function error values are indicated in bold.
4.3. Comparison on CEC2013 Test Functions
In order to further examine the effectiveness of the FA-MABC, it is compared with two FA variants (i.e., FADMF [23], FADCG [19]) and two ABC variants (i.e., IDABC [27] and ABCG [26]) on benchmark functions from CEC2013 with 30 variables. Since differential evolution (DE) and particle swarm optimization (PSO) are among the most widely used metaheuristic algorithms, the results of their recent variants, the multi-population ensemble DE (MPEDE) [34] and heterogeneous comprehensive learning PSO (HCLPSO) [35], are also included in comparison with the same of the FA-MABC. The MPEDE algorithm uses an adaptive ensemble of three mutation strategies [34]. The HCLPSO divides the entire population into two heterogeneous subpopulation groups and each subpopulation group is assigned to carry out the exploration and exploitation search separately [35].
The MPEDE, HCLPSO, FADMF, FADCG, ABCG and IDABC were recently tested to solve test problems from CEC2013. The results of FADMF and FADCG are taken from Ref. [19], while the results of the MPEDE, HCLPSO, ABCG and IDABC are taken from Ref. [27].
For fair comparison, value of
According to the comparison results in Table 5, the FA-MABC outperforms competing metaheuristic approaches in the majority of CEC2013 test functions. Concretely, the FA-MABC performs better than MPEDE, HCLPSO, FADMF, FADCG, IDABC and ABCG on 23, 28, 26, 27, 21 and 28 benchmark problems respectively. On the other hand, the FA-MABC is outperformed by the MPEDE, HCLPSO, FADMF, FADCG, IDABC and ABCG on 5, 0, 1, 0, 7 and 0 problems respectively. Overall, based on the obtained
5. DISCUSSION
In this section some experiments are performed with the aim to investigate impact of proposed algorithmic components on performance of the FA-MABC. Four different versions of the FA-MABC have been tested and compared against the proposed one on CEC2013 benchmark functions with 30
Version 1: To explore the effectiveness of using the FA algorithm with random attraction model as the global optimizer alone, a variant of the FA-MABC which excludes this algorithmic component is implemented. This version is denoted as the MABC.
Version 2: To investigate the impact of using the proposed multi-strategy ABC as the local optimizer alone, a variant of the FA-MABC which excludes this algorithmic component is implemented. This version is denoted as the FA-ra.
Version 3: To explore the impact of using the modified ABC search strategy given by Eq. (8) alone, a variant of the FA-MABC which excludes this search equation is implemented. This version is denoted as the MABC-FA1.
Version 4: To examine the impact of using the original ABC search strategy given by Eq. (5) alone, a variant of the FA-MABC which excludes this search strategy is implemented. This version is denoted as the MABC-FA2.
Each FA-MABC variant is performed over 51 independent runs for each benchmark function. Value of
| Fun. | MABC | FA-ra | FA-MABC1 | FA-MABC2 | FA-MABC | ||
|---|---|---|---|---|---|---|---|
| Mean error | Mean error | Mean error | Mean error | Mean error | |||
| 2.274e-13 | 9.616e-01 | 2.274e-13 | 4.972e-01 | 2.274e-13 | |||
| 1.250e+00 | 2.11e+00 | 9.999e-01 | 9.999e-01 | 9.965e-01 | |||
| 8.880e+03 | 3.500e+05 | 3.027e+04 | 3.038+04 | 8.771e+03 | |||
| 8.392+00 | 3.246e+01 | 9.029e+01 | 5.284e+00 | 5.402+00 | |||
| 3.411e-13 | 4.344e-01 | 3.411e-13 | 2.565e-01 | 3.411e-13 | |||
| 4.250e-08 | 1.494e-01 | 8.286e-04 | 8.112e-02 | 3.542e-08 | |||
| 1.092e-01 | 4.935e-01 | 3.572e-01 | 1.340e-01 | 1.056e-01 | |||
| 2.095e+01 | 2.129e+00 | 2.035e+00 | 3.607e-01 | 1.124e-01 | |||
| 1.235e+00 | 1.980e+00 | 4.399e-01 | 8.752e-01 | 7.448e-01 | |||
| 9.865e-03 | 4.779e-02 | 2.929e-02 | 2.920e-02 | 9.865e-03 | |||
| 5.684e-14 | 1.918e+00 | 5.684e-14 | 8.371e-01 | 5.684e-14 | |||
| 9.865e-03 | 4.770e-02 | 2.841e-02 | 2.875e-02 | 9.865e-03 | |||
| 3.829e+01 | 1.839e+00 | 9.071e-02 | 8.519e-01 | 2.842e-13 | |||
| 1.28e+00 | 5.072e+01 | 6.677e-02 | 2.135e+01 | 1.748e-12 | |||
| 2.632e+03 | 1.241e+01 | 9.876e+00 | 9.939e+00 | 8.463e-11 | |||
| 1.066e+01 | 9.303e-02 | 9.136e-01 | 2.515e+00 | 2.461e-01 | |||
| 3.916e-02 | 9.665e+01 | 6.798e-03 | 4.392e+01 | 1.430e-03 | |||
| 6.459e-08 | 7.580e+00 | 0.000e+00 | 5.169e+00 | 0.000e+00 | |||
| 4.854e-01 | 3.197e-02 | 3.308e-05 | 7.789e-03 | 3.411e-13 | |||
| 4.153e+00 | 1.396e+00 | 1.171e+01 | 6.779e+00 | 1.137e-13 | |||
| 1.137e-12 | 1.947e+02 | 1.137e-12 | 1.685e+02 | 1.364e-12 | |||
| 9.95e+01 | 1.538e+02 | 5.850e+01 | 1.348e+02 | 1.023e-12 | |||
| 4.787+02 | 1.394e+02 | 9.397e+01 | 1.285e+02 | 9.095e-13 | |||
| 9.095e-13 | 1.028e+02 | 3.383e+01 | 8.334e+01 | 9.095e-13 | |||
| 3.270e+02 | 1.030e+02 | 3.677e+01 | 4.064e+02 | 6.150e-13 | |||
| 2.273e-12 | 2.013e+02 | 4.088e+01 | 1.757e+02 | 2.501e-12 | |||
| 2.728e-12 | 2.009e+02 | 3.254e+01 | 1.766e+02 | 2.274e-13 | |||
| 2.274e-12 | 2.017e+02 | 5.790e+01 | 1.760e+02 | 2.274e-12 | |||
| 228/3 | 401/5 | 289/11 | 399/7 | - | |||
| 0.000 | 0.000 | 0.000 | 0.000 | - | |||
FA-MABC, firefly and multi-strategy artificial bee colony; ABC, artificial bee colony.
Comparison results of the MABC, FA-ra, FA-MABC1, FA-MABC2 and FA-MABC on CEC2013 benchmark functions with 30D D. The best mean of the function error values are indicated in bold.
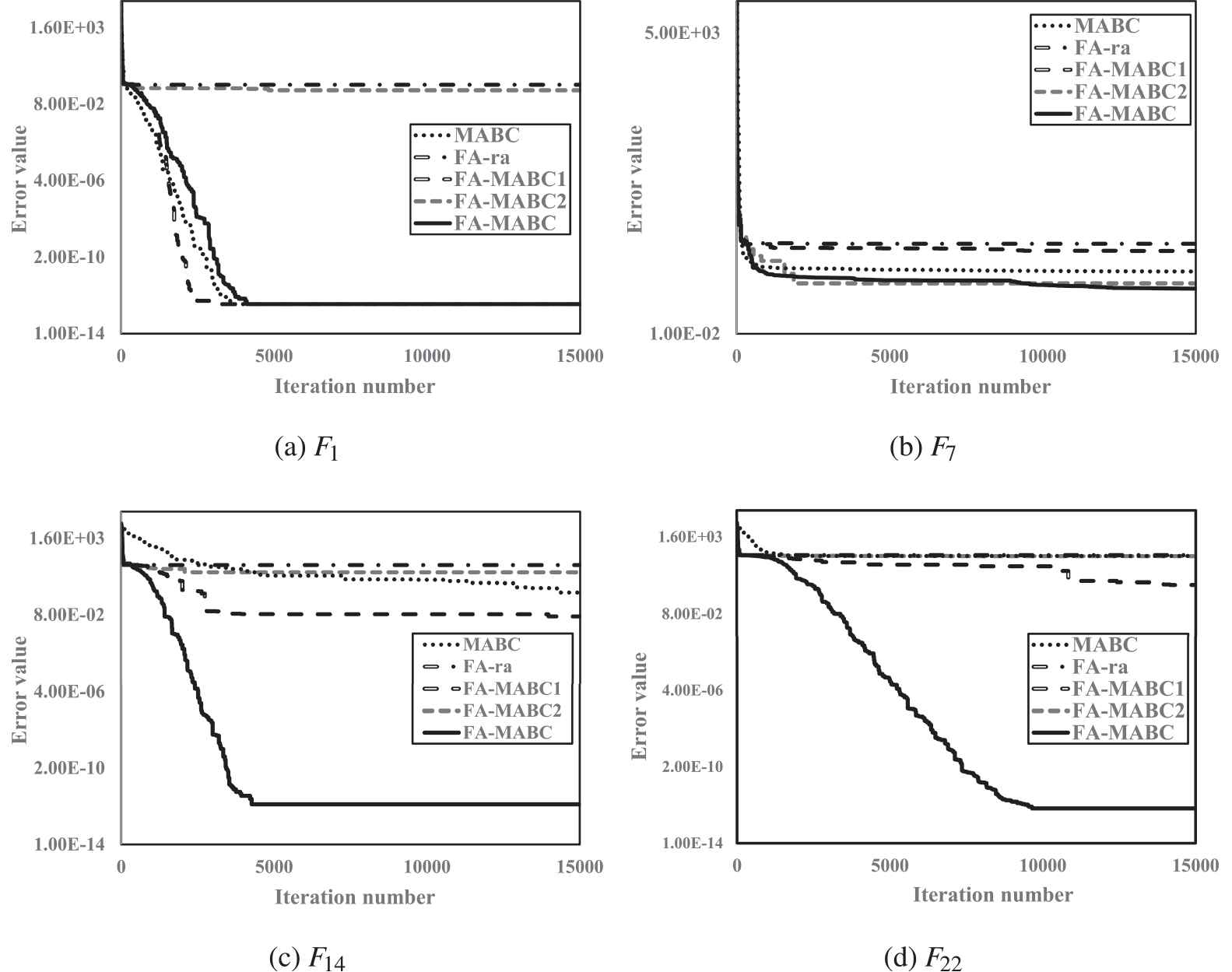
Convergence graphs of the mean function error values for the selected problems.
From Table 6 it can be seen that the FA-MABC outperforms each tested version on the majority of benchmarks. Concretely, the FA-MABC performs better than MABC, FA-ra, MABC-FA1 and MABC-FA2 on 19, 27, 22 and 27 benchmark problems respectively. On the other hand, the FA-MABC is outperformed by the MABC, FA-ra, MABC-FA1 and MABC-FA2 on 2, 1, 2 and 1 problems respectively. According to the obtained
These observations imply that each of the four algorithmic components significantly contributes to the good performance of the FA-MABC. Use of the FA with random attraction model helps the FA-MABC to discover the promising regions of the search space, while using the proposed multi-strategy ABC assists in reaching more accurate optimization results by performing intensive local search. Experimental results also confirm that the use of each suggested ABC search operators enables the FA-MABC to significantly improve the quality of the obtained solutions.
6. CONCLUSION
In this paper, a novel multi-stage collaborative hybrid algorithm based on the FA and multi-strategy ABC (FA-MABC) is proposed to solve numerical optimization problems. The FA with random attraction model performs global search whereas a novel multi-strategy ABC is developed to act as local optimizer.
The proposed FA-MABC efficiently utilizes the benefits of the FA and MABC through the two stages. In the first stage, the FA extensively explores the search space to find the promising areas. It is noticed that the FA can provide strong exploration ability, but it may show slow convergence rate due to its oscillatory behavior as the search process proceeded toward the optimum. To avoid stagnation of the search, the diversity measure is employed to determine when the output of the FA will be supplied as the input to the MABC. The MABC employs two search strategies with different advantages so that they complement each other during the search. The use of the efficient integration of different search operators and the selection mechanism can conduct a more refined search in the promising regions to improve both, the accuracy of the solutions and convergence speed.
In order to verify the performance of the FA-MABC, it is tested on a large set of numerical benchmark functions. The computational results showed that the FA-MABC significantly outperformed the basic FA and its five prominent variants, the basic ABC and its four outstanding variants and two other popular metaheuristic algorithms on majority of the benchmark functions. Also, experimental results validate that each algorithmic component, the FA with random attraction model, the multi-strategy ABC and each used ABC search strategy, significantly contributes to superior performance of the FA-MABC. In the future work, the performance of the FA-MABC applied to multi-objective optimization problems will be investigated. The FA-MABC can also be used to solve some practical optimization problems.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
AUTHOR CONTRIBUTIONS
Ivona Brajević proposed the main idea of the paper, implemented the algorithm, performed the experiments and wrote the major draft of the paper. Predrag S. Stanimirović contributed to the writing of the manuscript and in analyzing of the results. Shuai Li and Xinwei Cao reviewed the paper and provided helpful comments to further improve the quality of the paper.
FUNDING
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
ACKNOWLEDGMENTS
Predrag Stanimirović gratefully acknowledges support from the Ministry of Education, Science and Technological Development, Republic of Serbia, Grant No. 174013.
REFERENCES
Cite this article
TY - JOUR AU - Ivona Brajević AU - Predrag S. Stanimirović AU - Shuai Li AU - Xinwei Cao PY - 2020 DA - 2020/06/23 TI - A Hybrid Firefly and Multi-Strategy Artificial Bee Colony Algorithm JO - International Journal of Computational Intelligence Systems SP - 810 EP - 821 VL - 13 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.200612.001 DO - 10.2991/ijcis.d.200612.001 ID - Brajević2020 ER -
