Synchronization of Delayed Inertial Cohen–Grossberg Neural Networks Under Adaptive Feedback Controller
- DOI
- 10.2991/ijcis.d.200402.001How to use a DOI?
- Keywords
- CGNNs; Adaptive synchronization; Inertial term; Time-varying delay
- Abstract
This paper investigates the issue on adaptive synchronization of delayed inertial Cohen–Grossberg neural networks (ICGNNs). By adopting the method of variable transformation, the addressed model, which includes the so-called inertial term, is transformed into first-order differential equations. On the basis of the well-known invariant principle of functional differential equations, a novel and analytic scheme which ensures the adaptive synchronization between the drive-response system is proposed in component form. It is worth mentioning that we only need to impose one controller to the spilt systems to realize the adaptive synchronization, which is of less conservatism. At the end of this paper, a numerical example is provided to verify the feasibility of the derived theoretical results. The established figures validate that the numerical simulations coincide well with the developed theoretical results.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Neural networks(NNs) can be extensively applied in different fields, such as pattern recognition, parallel computing, image processing and so on. Therefore, they have been diffusely investigated in the past decades [1–7]. In order to realize these applications, it is necessary for people to study the dynamical behaviors of NNs, which greatly motivates the qualitative analysis of different dynamical behaviors [8–12]. In addition to stability, many other dynamical behaviors, including periodic oscillation, bifurcation, dissipation and synchronization, exist in real applications. Among them, the synchronization of NNs has developed into a issue of both theoretical and practical significance since synchronization is one of the most important issues related to their dynamic behaviors [13–15]. Moreover, time delays are inevitably encountered during the hardware implementation, which should be brought into the network model. Therefore, the synchronization problems of NNs with time delays have caused considerable attention and a great deal of works have been published, see [16–19] and references therein.
Particularly, the Cohen–Grossberg neural network(CGNN) model was initially established in 1983 [20]. It comprises a great deal of famous NNs, including Hopfield NNs, bidirectional associative memory NNs and cellular NNs. Consequently, the synchronization problem of CGNNs has also been proverbially studied due to their underlying applications in information processing, distributed computation and secure communication. For example, in [21–23], the synchronization problems of CGNNs with constant amplification gains and different delays were discussed. In [24], some synchronization criteria for delayed CGNNs were proposed by employing a periodic intermittent controller. In [25], Gan studied the adaptive synchronization of CGNNs with both mixed delays and unknown parameters.
Nevertheless, the existing studies mainly focus on the NNs with only first derivative of the states, and the effect caused by an inertial term is not taken into account. The introduction of the inertial term can be deemed as a key factor in generating chaotic behaviors, bifurcation and some other complicated dynamics in a networked system [26–30]. In addition, some synchronization conditions for inertial NN with or without Markovian jumping parameters were proposed in [31] and [32]. Based on the above discussion, it is obvious that the theoretical results for the synchronization of delayed ICGNNs are limited, which motivates the present research.
In the light of the well-known invariant principle, an adaptive feedback controller is provided to achieve the synchronization goal. Compared with previous research, the main contributions of the work are summarized in three perspectives: (i) The introduction of inertial term makes this problem more challenging, which has been successfully resolved based on the variable transformation method. (ii) We only need to impose one controller to the spilt systems, which is of less conservatism. (iii) The model considered in this paper is rather general, thus it comprises many existing results as its special cases.
The remaining part of the paper is organized as follows. The model description, necessary definition, lemma as well as assumptions are given in Section 2. A novel and analytic adaptive controller is presented in Section 3 to realize the synchronization of delayed ICGNNs. Moreover, an illustrative example is presented to validate the feasibility of the developed synchronization strategy in Section 4. At last, the conclusion of this work is made in Section 5.
2. MODEL DESCRIPTION AND PRELIMINARIES
In this paper, the delayed ICGNNs model can be described by the following differential equations:
Considering (1) as the drive system, the corresponding response system is devised as
The variable transformation is introduced as
Then, the above two systems are equivalent to
Denote the error signals as
To proceed further, the following hypotheses are utilized:
Before moving on, we present the following definition and lemma:
Definition 1.
The drive system (1) and the response system (2) is said to achieve synchronization, if the trivial solution of the error system (5) is asymptotically stable, i.e.,
Remark 1.
Since the drive-response systems (1) and (2) are equivalent to (3) and (4), respectively, the synchronization problem between (1) and (2) can be regarded as the synchronization problem between (3) and (4). In addition, according to the variable transformation, one can see that
Lemma 2.
[25] For any vectors
3. MAIN RESULTS
In this part, a new criterion is presented to achieve the adaptive synchronization of ICGNNs with time-varying delay. Besides, the corresponding corollaries of inertial NNs and delayed CGNNs are proposed.
Theorem 1.
If the hypotheses
Proof.
Constructing the following Lyapunov functional:
Calculating
Considering the assumptions
According to Lemma 2, one can derive that
Substituting (10) into the right side of (9), one can further obtain that
Letting
In light of (11) and (12), one has
Remark 2.
The synchronization issue of delayed ICGNNs are successfully resolved in Theorem 1. By means of variable transformation method, the original inertial system is split into two subsystems. By imposing an adaptive controller to subsystem 2, Theorem 1 has presented a componentwise scheme to assure the adaptive synchronization.
If we take
As a consequence, the corresponding response system is
Following the aforementioned variable transformation, the above two systems can be rewritten as
Following the same line as in Theorem 1, the following corollary can be readily obtained:
Corollary 1.
Suppose that the assumptions
Letting
Remark 3.
In [31], the authors discussed the synchronization problem of delayed inertial NNs based on the feedback controller. Compared with the model in that paper, Corollary 1 does not impose two controllers to the split drive system, which is of less conservatism.
When
For the drive system (20), the corresponding response system can be designed as
Analogously, we denote the error signal as
Corollary 2.
If the hypotheses
Letting
Remark 4.
In [16] and [21], the authors studied the synchronization of CGNNs with constant amplification gains, which could be deemed as a special case of Corollary 2. From the above discussion, it is obvious that the model considered in this paper is quite general and our results effectually improve several known ones.
4. A NUMERICAL EXAMPLE
Consider the following two-dimensional ICGNNs with time-varying delay:
The corresponding response system is presented as
By adopting the variable transformation, the above two systems can be rewritten as
It is obvious that
Moreover, for any
Since
Then the assumptions

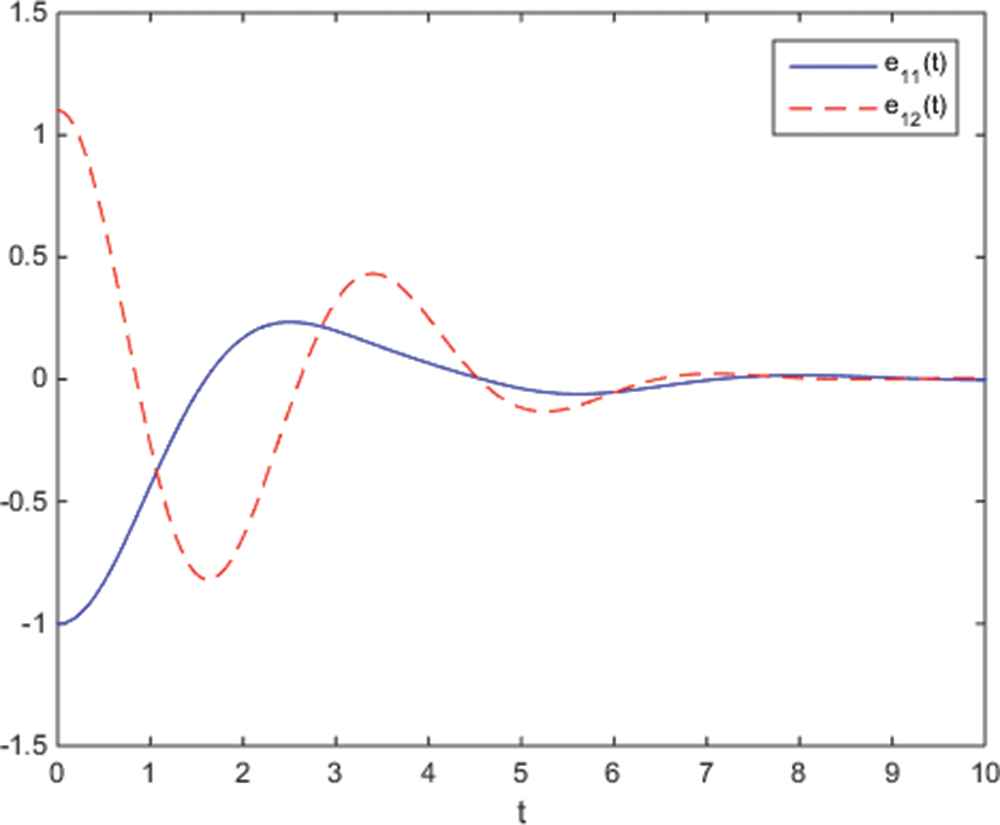
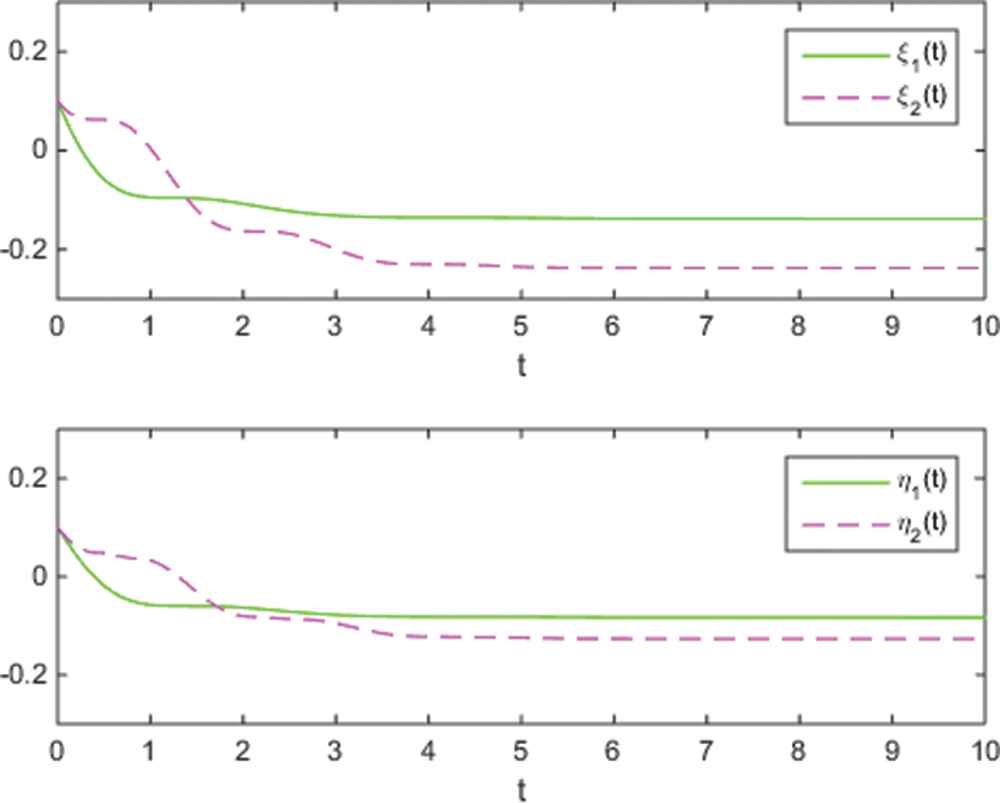
Dynamic behaviors of parameters
5. CONCLUSTION
Generally, the synchronization problem of delayed ICGNNs has been addressed in this work. The introduction of inertial term makes this problem more complicated and challenging. By employing the method of variable transformation, our synchronization criterion is presented in component form, which can be easily verified. It is also worth pointing out that our results comprise some conclusion appeared in the previous literature, as well as reduce restriction on the controller. In the end, a convictive example is proposed to demonstrate the feasibility of the adaptive strategy.
CONFLICT OF INTEREST
The authors declare that there is no conflict of interests regarding the publication of this article.
AUTHORS' CONTRIBUTIONS
Cao and Liu conceived and designed the study. Huang wrote the paper. Cao and Liu reviewed and edited the manuscript. All authors read and approved the manuscript.
ACKNOWLEDGMENTS
This work was partially supported by the National Natural Science Foundation of China under Grants 61573096 and 61833005, the Jiangsu Provincial Key Laboratory of Networked Collective Intelligence under Grant BM2017002. (Corresponding author: Jinde Cao.)
REFERENCES
Cite this article
TY - JOUR AU - Qun Huang AU - Jinde Cao AU - Qingshan Liu PY - 2020 DA - 2020/04/17 TI - Synchronization of Delayed Inertial Cohen–Grossberg Neural Networks Under Adaptive Feedback Controller JO - International Journal of Computational Intelligence Systems SP - 472 EP - 478 VL - 13 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.200402.001 DO - 10.2991/ijcis.d.200402.001 ID - Huang2020 ER -
