Optimized Intelligent Design for Smart Systems Hybrid Beamforming and Power Adaptation Algorithms for Sensor Networks Decision-Making Approach
- DOI
- 10.2991/ijcis.d.191121.001How to use a DOI?
- Keywords
- Optimized intelligent design for smart systems; Wireless network beamforming; Power adaption; Interference; Strategic decision-making; Game theory; Reinforcement learning
- Abstract
During last two decades, power adaptation and beamforming solutions have been proposed for multiple input multiple output (MIMO) Ad Hoc networks. Game theory based methods such as cooperative and non-cooperative joint beamforming and power control for the MIMO ad hoc systems consider the interference and overhead reduction, but have failed to achieve the trade-off between communication overhead and power minimization. Cooperative method using game theory achieves the power minimization, but introduced the overhead. The non-cooperative solution using game theory reduced the overhead, but it takes more power and iterations for convergence. In this paper, a novel game theory based algorithms proposed to achieve the trade-off between power control and communication overhead for multiple antennas enabled wireless ad-hoc networks operating in multiple-users interference environment. The optimized joint iterative power adaption and beamforming method designed to minimize the mutual interference at every wireless node with constant received signal to interference noise ratio (SINR) at every receiver node. First cooperative potential game theory based algorithm designed for the power and interference minimization in which users cluster and binary weight books along used to reduce the overhead. Then the non-cooperative based approach using the reinforcement learning (RL) method is proposed to reduce the number of iterations and power consumption in networks, the proposed RL procedure is fully distributed as every transmit node require only an observation of its instantaneous beamformer label which can be obtained from its receive node. The simulation results of both methods prove the efficient power adaption and beamforming for small and large networks with minimum overhead and interference compared to state-of-art methods.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Ad Hoc multiple input multiple output (MIMO) communication system is base for the future generation wireless communication system Massive MIMO. Multiuser-MIMO (MU-MIMO) boosts the design and development of Massive MIMO technologies [1]. MIMO communication system efficiency mainly depends on adaptability of transmit parameters such as beamformer selection, transmit power, transmission rate, modulation technique, and so on. The design of beamformer selection plays the important role for the adaptive wireless communication systems. For MIMO, the beamforming methods designed for different types of networks such as point-to-point, cellular, and ad hoc [2]. Number of beamforming methods designed to address the challenges related to each of such networks. The conventional method of beamforming shows the power control, throughput maximization, and capacity enhancement especially for point-to-point and cellular networks. For MIMO ad hoc networks, the distributed beamforming solutions show the system throughput enhancement and energy minimization but suffer from the challenges of interference and communication overhead. Several distributed beamforming methods were designed to minimize the interference and communication overhead in literature.
As discussed earlier, there are three categories in which the beamforming solutions presented for MIMO. The point-to-point communication based MIMO beamforming solutions described in [3–6] and the beamformers and linear precoders (eigencoders) proposed for point-to-point MIMO communications in [7,8]. The beamforming algorithms designed for the cellular networks in [9–11] reduces the power and improve the capacity of single antenna mobile transmitters and array-equipped base stations. The beamforming and power control for point-to-point and cellular MIMO networks achieved with minimum overhead and interference challenges. However, the problem is for ad hoc MIMO networks where operate without centralized controller and moving nodes. For MIMO ad hoc networks, the distributed beamforming techniques enhance network throughput and minimize energy consumption [12,13]. The main challenge using optimization based solutions for ad hoc networks is that they needs the systematic and proper study as the environment of such networks is interference limited as well as overhead introduced by beamforming algorithms affects the performance of MIMO ad hoc networks. Earlier were distributed spatial beamforming techniques introduced in [14,15] for multi-user ad hoc MIMO networks under channel reciprocity conditions. However, in such methods the transmission overhead is introduced during the power control and at each iteration. To minimize the communication overhead. Further, many iterative algorithms were introduced for ad hoc MIMO networks. However, the trade-off is not achieved with such techniques as well as convergence of iterative algorithms has not been investigated.
On the other hand, there are a lot of formats can view the information structure that allowed a full understanding and showed a good view of the problems that we are interesting to, when the predictive are enabling such its capability can be determined in order to enhance the view of information such that (modify, reinforce, or maybe reject). Mathematical modeling such that game theory and information theory can capture important reality features and meaningful data structure in a manageable manner with efficient information processing to achieve a smart and trust decision-maker strategies, a qualified intuition is strongly needed. A good decision aid methodology implies understanding reality in a manageable way [16]. Game theory is useful mathematical tools for Studying environments where multiple players are interacting and making decisions, it often talk about rational players (they try to optimize their own interests) [17].
The Game theory based solutions produced the efficiency along with convergence investigation for important problems in wireless communications like joint code-division multiple access [18], distributed power control algorithm [19], and optimum transmission signaling strategies [20,21]. Thus, game theory based beamforming and power adaptation methods designed for multi-user ad hoc MIMO network communications to achieve the power efficiency with minimum overhead. In [22], the initial cooperative and non-cooperative game theory based methods designed for joint channel and power control for wireless mesh networks, and chanel allocation and beamforming for ad hoc networks was studied in [23], however the solutions are suboptimal for wireless communications. For ad hoc networks the reduction of power using the distributed algorithms and transmit beamformer selection is difficult tasks and hence its challenging to formulate the beamforming games for multi-user wireless communications. In [24,25], the first attempt over joint discrete transmits beamforming and power adaptation introduced using the cooperative and non-cooperative game theory based solutions. The decentralized approach designed for optimizing the transmit beamformer and power adaptation by exploiting the local information with the acceptable computational burden under constraint of constant received target signal to interference noise ratio (SINR). However, designing the optimized game theory based approach for the power adaptation and beamforming in ad hoc MIMO systems is still the complex research problem the both solutions failed to achieve the trade-off between power minimization and overhead. In [25], the first solution cooperative power minimization algorithm (COPMA) achieved the power minimization but introduced the overhead and second non-cooperative solution regret-matching-based joint transmit beamformer and power selection game (RMSG) minimizes the communication overhead but it takes more power and iterations to converge. In this paper, we further optimize COPMA and RMSG techniques to minimize the overhead and power consumption respectively. In [26] the reinforcement learning (RL) based algorithm used to determine the suitable policy for selection between two different techniques, first one is beamforming while the second is power control for sensor array networks, by taking the benefit of the individual features of each method according to SINR threshold. The key issue of the RL is to select the action (BF or PC) according to the learning state in this case (SINR), that is satisfied with the system requirement. Q-learning with an epsilon greedy (ε-greedy) policy was used in the RL algorithm that is trained by using the offline method. Artificial intelligence (AI) techniques have been described and applied in problems for beamforming, power control, and MIMO wireless communication systems [27–30].
The key contributions of this paper summarized as:
Enhanced co-operative power minimization algorithm (ECOPMA) for MIMO Ad hoc networks is proposed to overcome the challenges of COPMA. We proposed cooperative method using the potential game approach in which first compute allocated power and beamformer for each user until the convergence to the steady state according to Nash equilibrium (NE) technique, then divide users in clusters [31] and enable them to converge at same time in order to minimize the overhead. In short, in this case the users cooperate each other to reduce the power and interference using the potential game theory and NE.
To reduce the communication overhead in ECOPMA, the binary weight books are used rather than using the complex Grassmannian weight books. The binary weight book reduces the overhead incurred by cooperative solution.
Proposed reinforcement learning based power allocation and beamformer algorithm (RLPBA) for multi-user ad hoc MIMO systems. In RLPBA, optimized non-cooperative solution designed using the RL game based approach in which the local information used for the beamforming and power adaption decisions. The Reinforcement approach propose to reduce the number of iterations and hence the transmit power for convergence.
Extensive experimental results and comparative evaluations presented for ECOPMA and RLPBA with centralized and state-of-art cooperative and non-cooperative algorithms.
In Section 2, the proposed system model, algorithms for ECOPMA and RLPBA presented. In Section 3, the simulation results are discussed. In Section 4, conclusion and future work described.
2. METHODOLOGY
This paper proposes the two technologies ECOPMA and RLPBA proposed to address the challenges of power minimization with minimum interference and communication overhead with guaranteed QoS for multi-user MIMO ad hoc systems with constant SINR constraint. ECOPMA is based on potential cooperative games using binary weight books rather than using the complex Grassmannian weight book to reduce the communication overhead. ECOPMA is similar to the COPMA [25] with inclusion of binary weight books. The RLPBA is non-cooperative games based power allocation and beamforming technique similar to RMSG [25] with use of reinforced learning to reduce the power consumption and number of iterations to converge. In Section 2.1, we present the MIMO ad-hoc communication model and game theory problem. In Section 2.2, we present the design of centralized beamforming and power allocation technique. In Section 2.3, design of ECOPMA presented, in Section 2.4, the design of RLPBA described.
2.1. System Model
Figure 1 demonstrates the system model referred from [25] which consist of wireless ad hoc systems with multiple antennas nodes pair under the same channel. The interference generated by other nodes pairs operating on similar channel. Total N number of node pairs with each pair q consist on single transmit-receive wireless node. Every transmitting and receiving node is equipped with A antennas. Every node having the beamformer pair
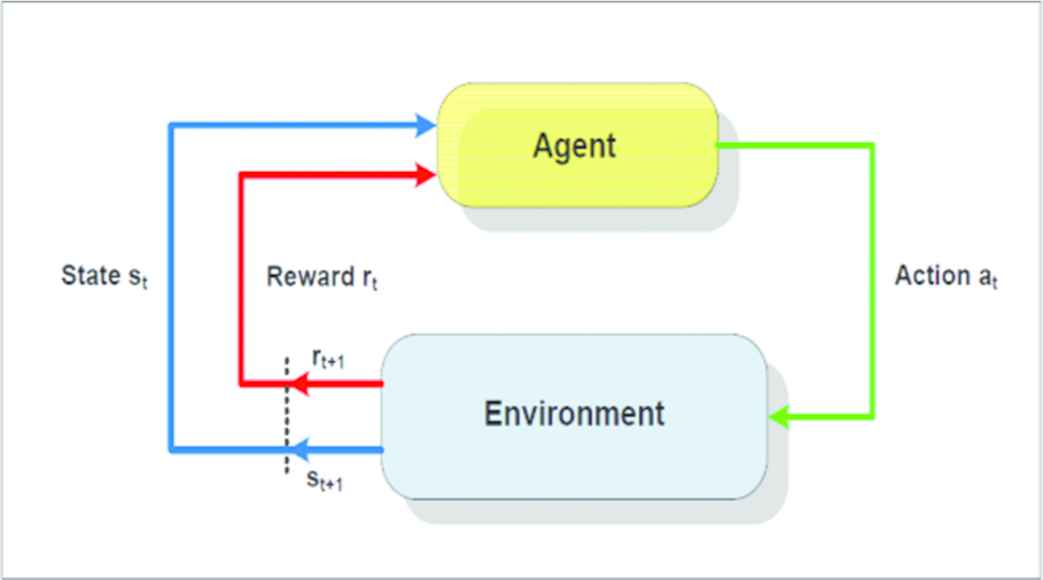
Environment and agent system interaction method [26].
The worst case is considered in this work in which all the pairs always having packets to transmit through the wireless channel. The network assumed to be synchronous. The available codebook beamformers set for the
Thus the proposed methods in this work attempt to achieve the target SINR through the transmit powers adjustment. According to this, the optimization problem of this work is described as below.
The objective is to reduce the transmit energy of all the nodes pairs
This problem is represented in game theory approach as normal form of game as:
2.2. Centralized Method
Prior discussing the decentralized solutions, this section we formulate the centralized solution for MIMO ad hoc communication systems. Using the centralized agent [32], joint transmit beamfomers and corresponding transmit powers selected to reduce the overall transmit power of all the antennas as:
In this case, the centralized agent computers the total network power for ϒN possible beamforming vector combinations which leads the complex tasks in case large scale wireless ad hoc networks. The sever complexity invalidates the centralized method for multi-user MIMO ad hoc systems. To solve such problems we introduced the decentralized solutions in this paper.
2.3. ECOPMA
As the name indicates, ECOPMA is cooperative game based solution (Where nodes can cooperative each other to achieve the optimum solution) for beamforming and adaptive power allocation for multi-user MIMO ad hoc systems. As discussed earlier, the ECOPMA is similar to COPMA [25] in which we used the two users paired in clustering and binary codebook to reduce the computational overhead. In this work, we generated the binary codebook of size 16 (represented as ϒ) code length and 4 (represented as A) is dimension of code [33].
The clustering mode, in which we assume that the node pairs with similar transmit power properties are grouped into one cluster. The mobile users clustered in order to enable them to converge at same time to minimize the energy and overhead. In [34], it is proved that for multi-user scenario, two users paired into cluster leads to common transmit beamforming vector sharing and hence improves the QoS performance with minimum overhead and power consumption. In ECOPMA, finding the joint optimal transmit power allocation and transmit beamformer so that total power consumption in network is minimized. Let the each user in
Eq. (9) will assume as the every users utility function that is,
The special case of potential games is modelled in this paper called identical interest game [25,35]. Therefore it becomes easier to verify that at least one pure NE produced by all the identical interest games which represent any action profile that enhances
Algorithm 1 ECOPMA
1. Inputs:
k: predefined number of iterations
M = number of clusters
2. Apply the users clustering on all the mobile users regardless of users pairing
3. FOR each cluster m in M, do
4. Initialization: For each pair q, initialize transmit beamfoerms and transmit powers:
4.1.
4.2.
5. Repeat: random selection of
5.1. Set
5.2. Calculate
5.3. Random selection of transmit beamformer
5.4. Form a vector
5.5. On receiving data vector, for each j
IF (
Every other node pairs sets
Computes new transmit power and set it as
ELSE
Unchanged
END
Send back vector
5.6. node pair q computers the total network transmit power as
5.7. Updating node pair q selects the
5.8.
5.9. If not kept, then every other node pair j,
6. Until predefined number of iterations steps k
7. END FOR
The functionality of smoothing factor is referred from [25] with the core contribution of this research paper. The above Algorithm 1 shows the difference between COPMA [25] and ECOPMA using the clustering. The
2.4. RLPBA
The second solution proposed in this paper is based on non-cooperative game theory based approach for beamforming and adaptive power allocation in multi-user ad hoc MIMO systems using the RL scheme. The main aim is to design the distributed learning technique for joint transmits beamformer and power selection scheme which needs only local information for updates for ad hoc MIMO systems. The utility function for non-cooperative users used in this case. As compared to cooperative solution, the
One of the important methods in Temporal-Difference (TD) methods is Actor-Critic which based on separated memory structure in order to describe the independent of policy as compared with the value function (as contrasted with the reward
As like in Figure 1, let S denotes the number of states required that contains the
Every user q computes the
After updation, we perform the selection the transmit beamformer
Every user q chooses an action or strategy according to the outcome of
According to the selection of transmit beamformer
Algorithm 2 RLPBA
Inputs
k: predefined number of iterations
1. FOR i = 1, 2,…, k
2. FOR q = 1, 2,…, N
3. Compute the reward value using Eq. (11)
4. Update Reward table using Eq. (12)
5. Compute the probability values using Eq. (13)
6. Take the decision on
7. Compute new transmit power for
8. END FOR
9. END FOR
3. SIMULATION RESULTS AND DISCUSSIONS
This section presents the performance investigation of proposed ECOPMA and RLPBA methods with state-of-art solutions such as centralized optimization, RMSG [25], and COPMA [25]. While evaluating such methods we designed ad hoc networks with assumption of 5 (small) and 10 (large) homogenous pairs with each having one transmitter and receiver node. The complete sets of parameters are described for 5 pairs and 10 pairs in Tables 1 and 2 respectively. For COPMA [25], the Grassmannian codebook of size ϒ = 16 with A = 3 antennas for all users, however as the Grassmannian codebook complex, for ECOPMA we used binary codebook of size ϒ = 16 with A = 4 antennas for all users in this work.
| Parameter | Value |
|---|---|
| Number of wireless ad hoc pairs | 5 |
| Size of network | 30 m × 30 m |
| Constant Received SINR | 10 dB |
| Grassmannian codebook | (ϒ = 16, A = 3) |
| Binary codebook | (ϒ = 16, A = 4) |
| 100 mW | |
| 1 mW | |
| Propagation channel | Radio propagation channel (path loss component is 4) |
| Predefined number of iterations (k) | 120 |
| Smoothing factor (For COPMA and ECOPMA) | |
| Clusters (ECOPMA) | 2 |
| Methods Investigated | Centralized, COPMA, RMSG, ECOPMA, and RLPBA. |
Notes. COPMA = cooperative power minimization algorithm; ECOPMA = enhanced co-operative power minimization algorithm; MIMO = multiple input multiple output; RLPBA = reinforcement learning based power allocation and beamformer algorithm; RMSG = regretmatching-based joint transmit beamformer and power selection game; SINR = signal to interference noise ratio.
Simulation parameters for 5-Pairs wireless ad hoc MIMO system.
| Parameter | Value |
|---|---|
| Number of wireless ad hoc pairs | 10 |
| Size of network | 100 m × 100 m |
| Constant Received SINR | 10 dB |
| Grassmannian codebook | (ϒ = 16, A = 3) |
| Binary codebook | (ϒ = 16, A = 4) |
| 100 mW | |
| 1 mW | |
| Propagation channel | Radio propagation channel (path loss component is 4) |
| Predefined number of iterations (k) | 1500 |
| Smoothing factor (For COPMAand ECOPMA) | |
| Clusters (ECOPMA) | 4 |
| Methods Investigated | Centralized, COPMA, RMSG, ECOPMA, and RLPBA. |
Notes. COPMA = cooperative power minimization algorithm; ECOPMA = enhanced co-operative power minimization algorithm; MIMO = multiple input multiple output; RLPBA = reinforcement learning based power allocation and beamformer algorithm; RMSG = regretmatching-based joint transmit beamformer and power selection game; SINR = signal to interference noise ratio.
Simulation parameters for 10-Pairs wireless ad hoc MIMO system.
3.1. Evaluations of 5-Pairs Wireless Ad hoc System
Table 1 shows the simulation parameters to use to investigate said methods.
As per the above table which is designed for small ad hoc networks evaluations, we measured the performance of total power consumption. Figure 2 demonstrates the comparative analysis of total power consumed by network for cooperative methods COPMA and ECOPMA. The purpose of ECOPMA is to reduce the overhead by reducing the number of iterations compared to COPMA method which is achieved in results (Figure 2). We observe that ECOPMA's performance settles at the global optimum combination after 87 iterations as compared to COPMA (93 iterations). The reduction in iterations reduces the communication overhead as well as total power consumption of network. The performance of ECOPMA is improved due to the clustering and simple binary codebook. Similarly we evaluated the non-cooperative distributed learning based techniques in Figure 3. The RLPBA designed to reduce the power consumption with the reduction of iterations for optimum allocation solutions for network pairs. We exploited the advantages of RLtechnique over the regret based learning approach in RLPBA. The outcomes of RLPBA show that it reduced the total transmission power for small wireless ad hoc MIMO networks compared to RMSG technique. It takes 110 iterations to converge total network transmission power compared to RMSG (120 iterations).

Total transmit power versus iterations (N = 5) for cooperative methods evaluations.

Total transmit power versus iterations (N = 5) for non-cooperative methods evaluations.
Figure 4 demonstrates the comparative study of all the methods. It shows that total power in network varies using the non-cooperative methods over the 120 iterations. The cooperative methods (COPMA and ECOPMA) achieved the better total transmit power reduction performance compared to non-cooperative methods (RMSG and RLPBA). But the cooperative methods introduced the significant overhead compared to non-cooperative methods. The updating task needs less overhead for non-cooperative methods. The proposed cooperative and non-cooperative achieved the optimum performances compared to existing solutions in this paper.

Total transmit power versus iterations (N = 5).
Figure 5 demonstrate the power trajectories in ECOPMA for every user pair in network. As observed in figure, every user starts with maximum power levels initially (i.e., 100 mW), and then power is updated iteratively as per the behaviur of ECOPMA algorithm till the NE achieved.

Transmit power versus iterations with N = 5.
Figure 6 demonstrates the variations in probability mass function (P.M.F.) of RLPBA method computed by Eq. (13) after iterations 1, 12, 50, and 100 for single user. At the start, the user selects the transmit beamformers with equal probability, further it changes according to working RL.

Probability mass function (P.M.F.) of based power allocation and beamformer algorithm (RLPBA) method for single user (N = 5).
3.2. Evaluations of 10-Pairs Wireless Ad hoc System
Table 2 shows the simulation parameters for large wireless ad hoc MIMO systems performance evaluations using the different methods. As observed in Table 2, the network area, smoothing factor, and number of clusters changed as per the network topology compared to Table 1 parameters.
Similar to scenario of N = 5, we computed the performance of cooperative, non-cooperative, and all methods in Figures 7–9 respectively for total transmission power of network.

Total transmit power versus iterations (N = 10) for cooperative methods evaluations.

Total transmit power versus iterations (N = 10) for non-cooperative methods evaluations.

Total transmit power versus iterations (N = 10).
The results demonstrate that using the proposed cooperative and non-cooperative methods, we achieved the total transmission power minimization and overhead reduction compared to existing methods cooperative and non-cooperative methods. A proposed solution reduces the number of iterations to achieve the NE and hence delivers the highest throughput compared to existing techniques. The centralized approach is no longer feasible in this scenario due to the enormous strategy space required [25]. As seen in Figure 9, the cooperative methods achieved the reduction in total transmit power as compared to non-cooperative as they converge early. The non-cooperative methods takes too much iterations to achieve the NE step, hence failed to reduce the transmit power, but it take the minimum overhead compared to co-cooperative solutions. For N = 10, the proposed solutions further optimize the cooperative methods. The RLPBA reduced the number of iterations for convergence and hence total transmit power reduction compared to RMSG. Figure 10 demonstrates the variations in P.M.F. of RLPBA method computed by Eq. (13) after iterations 1, 500, 1000, and 1500 for single user in this scenario as well.

Probability mass function (P.M.F.) of based power allocation and beamformer algorithm (RLPBA) method for single user (N = 10).
The proposed solutions achieved the reduction in communication overhead compared to previous methods. The clustering with binary coodbook for cooperative method helps to reduce the communication overhead as compared to COPMA and the RL helps to reduce communication overhead compared RMSG techniques.
4. CONCLUSION AND FUTURE WORK
In this paper we initiated our study on design of beamformer selection and it's the important role for the adaptive wireless communication systems. We proposed two game theory based algorithms to optimize the performance of ad hoc wireless MIMO systems for joint transmit power and transmit beamforming with minimum power consumption and overhead. We designed cooperative (ECOPMA) solution using clustering and binary codebook and non-cooperative (RLPBA) solution using the distributed reinforce learning in this paper. The simulation outcomes demonstrate the convergence properties of the proposed techniques and their performance in terms of overall power minimization, convergence rate, and communication overhead in network. The proposed solutions achieved the significant performance improved compared to state-of-art methods. For future work, we further suggest to investigate performance under different propagation channels and Signal to Interference Noise Ratio (SINR) constraints.
REFERENCES
Cite this article
TY - JOUR AU - Ali Kamil Khiarullah AU - Ufuk Tureli AU - Didem Kivanc PY - 2019 DA - 2019/11/27 TI - Optimized Intelligent Design for Smart Systems Hybrid Beamforming and Power Adaptation Algorithms for Sensor Networks Decision-Making Approach JO - International Journal of Computational Intelligence Systems SP - 1436 EP - 1445 VL - 12 IS - 2 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.191121.001 DO - 10.2991/ijcis.d.191121.001 ID - Khiarullah2019 ER -
