Adaptive Fuzzy Mediation for Multimodal Control of Mobile Robots in Navigation-Based Tasks
Authors contributed equally
- DOI
- 10.2991/ijcis.d.190930.001How to use a DOI?
- Keywords
- Fuzzy mediation; Adaptive control; Mobile robot; Neural networks; Teleoperation
- Abstract
The paper proposes and analyses performance of a fuzzy-based mediator with showcase examples in robot navigation. The mediator receives outputs from two controllers and uses estimated collision probability for adapting the signal proportions in the final output. The approach was implemented and tested in simulation and on real robots with different footprints. The task complexity during testing varied from single obstacle avoidance to a realistic navigation in real environments. The obtained results showed that this approach is simple but effective.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Autonomous mobile robots and vehicles are getting out of structured and laboratory-type environments into more dynamic environments [1–5]. Due to the uncertain nature of these environments, a robot's behavior needs to be adaptive in order to work properly without human intervention or with minimal human intervention. These environments range from air-, water- and ground-based ones to space-based ones [1,4]. The paper focuses on ground-based autonomous mobile robots, but some of its conclusions could be extended to other domains (like air and water). Thus, the term autonomous mobile robots will refer to ground-based mobile platforms.
When considering the application of autonomous mobile robots, usually two main concerns are of interest: long-term autonomy and safety [1], especially in light of human–robot cooperation. This has been highlighted by the fact that several recent EU-, USA-, and Japan-based projects consider safety as the main challenge in human–robot interaction [2]. In order to alleviate these concerns, researchers usually provide a robot with an appropriate form of artificial intelligence. The current state-of-the-art approaches use some form of Deep Neural Network (DNN) [6] in conjunction with a fusion of data from several sources which is referred to as deep multimodal learning [3]. While deep multimodal learning approach has found many interesting applications within recognition and classification fields (e.g., Ref. [7]), applications to autonomous robot navigation are scarce (but do exist, e.g., Refs. [8–10]). One notable exception is semi-autonomous cars [3,11,12], which also have well-known and large databases available for testing and benchmarking new approaches [13,14]. The fusion itself can be achieved on three levels [3,15]: feature level (sometimes referred to as early fusion or pre-mapping fusion), decision level (sometimes referred to as late fusion or post-mapping fusion), and mid-level (sometimes referred to as intermediate fusion or midst-mapping fusion). Some variations exist within each of these high-level fusion architectures (e.g., Ref. [16]). Regardless of which fusion scheme is used “most multimodal deep-learning architectures proposed to date are meticulously handcrafted” [3]. Even a minor modification to the neural network (NN) task usually require re-training the whole network or training it from scratch, which is a time-intensive procedure (especially in multimodal networks). This is due to the fact that (D)NNs are designed to do one specific task for which they require large amounts of training data (usually images/videos) [17]. Additionally, one would like to have an approach which enables combining (D)NNs with other control algorithms already present in robotics (like Proportional-Integral-Derivative [PID] controller) as well as integrating human input into control scheme (like in teleoperation scenarios).
In the field of control theory there have been approaches where more complex behavior is achieved through mediation between expert and novice controllers [18]. The ultimate goal of the mediation is to “help the autonomous capabilities of an individual … and to help individuals with different conflicting interests or diverging opinions to mediate situations and reach consensus” [19]. Thus, more complex tasks (such as robot navigation) could be split into several simpler ones (which we refer to as task primitives), and each can be addressed by a different controller including (but not limited to) (D)NNs. By using the proposed control architecture the modifications in task primitives (e.g., adding another task primitive) should require less time-consuming interventions. Also, such modularity would ensure easier upgrade procedure as well as the implementation of more specialized (and better performing) controllers for the particular task (which could be done even on the fly). To the best of our knowledge, this is the first time to date such an adaptive fuzzy-based controller, which can include NNs, is used in mobile robot navigation tasks and its performance demonstrated in real-world scenarios.
1.1. Related Work
Since state-of-the-art approaches use predominantly NNs to tackle the intelligent robot control, we will focus on them in the review.
In Ref. [20] authors implemented end-to-end motion planning for mobile robots in which they trained (in a supervised manner) a Convolutional Neural Network (CNN) using simulated sensor data gathered in Stage 2D environment. The term end-to-end control refers to the fact that the input data was directly mapped to the (translational and rotational) steering commands. The training data was recorded while navigating in a simulation on a known map using Robot Operating System (ROS) [21] 2D Navigation stack with its local (Dynamic Window Approach [DWA]) and global (Dijkstra) planners. However, when testing was done (both in a simulation environment and in real-world using Kobuki-based Turtlebot), no map was given to the robot but only the relative distance to the target. Thus, in essence, the CNN was applying navigation strategies learnt during training. The approach showed promising results, being able to navigate to the desired location in the real-world without the need for a map while avoiding moving obstacles (although testing was limited). However, the authors outlined several situations where the control algorithm needed a bit of help to get “unstuck”: large open spaces and convex dead-end regions. The incidence rate of human assistance dropped if additional fully connected (FC) layers were added (this was not true for simulation-based environments). It should be noted that work from Ref. [20] has some similarities with our own work: using 2D Light Detection and Ranging (LiDAR) data instead of a video stream for NN training, using simulation as a source of data for self-supervised learning and navigating without the need for a map. However, our approach achieves those goals in a different manner within the framework which we believe to be more flexible and which can integrate additional, standard, control algorithms. We also use both positive and negative examples for training. Successful obstacle avoidance is regarded as a positive example, while the crash is considered a negative example in the process.
Similar works that used some form of NN to learn end-to-end policies can be found in Refs. [22,23]. In Ref. [22] it was examined if end-to-end training of both the visual and the control system provides better performance than in the case when they were trained separately. These policies were represented by deep CNNs with supervised learning approach via guided policy search. While the paper mainly deals with the application of visuomotor polices on robot manipulator tasks (e.g., screwing a cap onto a bottle, placing a coat hanger on a rack), some of its conclusions can be transferred to a mobile robot case. One such conclusion is the fact that the end-to-end approach outperformed approach in which vision layer was trained separately. Although some drawbacks associated with generalization and visual distractors were noted, authors suggest straightforward ways of dealing with them. In Ref. [23] an end-to-end approach was also used with steering angles obtained from raw input images. This was achieved using CNN with six layers, trained in a supervised manner using data obtained from a human operator in real-world in various weather conditions and terrains. The training set consisted of
Additional works in the area of autonomous navigation include Refs. [8,11,25–27]. In Ref. [26] authors did not use end-to-end approach but developed a long-range vision system based on DNNs which interacted with path planning and obstacle avoidance algorithms in order to generate steering commands. The long-range vision module was trained in real-time in a self-supervised manner with stereo supervisor taking care that data and label are not changed. The supervisor involved a number of algorithms (like ground plane estimation, and statistical false obstacle filtering) which interacted in a complex manner. The long-range classifier demonstrated obstacle detection capabilities from 5 to over 100 meters. The approach was tested in two separate scenarios. First, the classification network was tested as a standalone system where different network architectures were applied. It was shown that hybrid unsupervised/supervised approach performs the best (with error rates of about
In Ref. [27] visual-based system (from a first-person view) was also used, but now for an indoor environment and in an end-to-end manner. Here, a complex structure of several NNs was used in order to map the space and navigate through it. Used NNs were of convolutional type (ResNet-50 pretrained on ImageNet). The process is a reminiscence of Simultaneous Localisation and Mapping, but authors note that their approach differs in several ways from classical approaches one being that it can learn statistical regularities of the environment. Thus, the approach enables tracking of visited parts of the environments as well as semantically driven navigation (e.g., “go to a table”). The proposed approach was developed in the simulated environment, based on Stanford large-scale 3D Indoor Spaces (S3DIS) data-set which was obtained by 3D scanning of six large-scale indoor spaces within three different buildings. Obtained results demonstrated that the proposed approach outperforms classical approaches such as reactive strategy and standard memory-based architectures (e.g., Long-Short Term Memory).
Here, it is interesting to note the use of simulation-based data for training of CNNs (or other types of NNs). Due to a large amount of data needed to properly train different NN architectures, collecting them in real-world is a time-consuming task and one in which certain level of danger to environment and robot itself cannot be avoided [28]. The simulation makes it easy to run extensive and elaborate experiments while providing necessary data in a safe and controlled manner. While in some works like Refs. [11,27,29] the training and the testing were achieved in the simulation environment, this is not optimal since a gap between simulation and reality exists [30]. However, recently a number of works have emerged where testing of simulation trained CNNs was done in real environments with no or little re-training [8,31]. This is mainly due to recent advances in the field of computer graphics which makes possible a rich and vivid representation of real-world environments as well as their physics, thus narrowing the before-mentioned gap. However, another more recent approach is to use a combination of photo-realistic data in conjunction with nonphoto-realistic domain randomized data to leverage the strengths of both [32]. This approach was then used to learn the object's 3D pose from RGB images, outperforming state-of-the-art NNs trained on real images.
In Ref. [8] authors used deep siamese actor-critic model within deep reinforcement learning (RL) framework for target-driven visual navigation. For the approach model was given an RGB image of the current scene and additional RGB image of the target, providing as output required action: moving forward, moving backwards, turning left, and turning right. Authors highlight that in this manner their RL approach becomes more flexible to changes in task goals (in contrast to more standard approaches like Ref. [33] in which the goal is hardcoded in the NN). In order to achieve this, the authors developed custom 3D simulation framework named AI2-THOR (The House Of inteRaction) by providing reference images to artists which then created realistic 3D environments (32 scenes in total). The approach was tested both in simulation and in the real environment with SCITOS mobile robot. Obtained results from simulation showed shorter average trajectory length for the proposed approach when compared to baseline methods, while results from real-world experiment demonstrated that network trained in simulation and fine-tuned on real data converged faster than network trained from scratch. Authors especially emphasize that their approach is generalizable to new scenes and new targets.
In Ref. [31] authors went a bit further, developing a NN model solely in simulation and applying it in the real-world without any modification. It was used for searching for control policy which can process raw data (e.g., images) and output control signals (velocity), and which relied on RL. Since, as authors outline, RL needs at least some collisions (negative examples) during training it can be a challenging and risky undertaking to train a mobile robot on real-world data. To avoid real-world training authors used Blender, an open-source 3D modelling suite, to construct a number of hallway-based environments (24 using 12 different floor-plans) for generating data used for training deep fully CNN with dilation operations, built on VGG16 architecture. It is interesting to note that authors intentionally rendered environments with a lower degree of realism and/or visual fidelity and ones with randomized textures, lighting conditions, and obstacle placement and orientation. This was based on the hypothesis that generating a large number of such environments with numerous variations (of textures which there were 200) would produce a model which generalizes well. This hypothesis was verified in experiments both in synthetic and real environments. The simulation-based testing showed that the proposed RL approach outperforms used baseline methods (Straight controller and Left, Right and Straight [LRS] controller), but in real-world testing experience some collisions. This led the authors to conclude that the proposed approach is viable and that further testing is needed such as the inclusion of additional sensors (like RGB-D cameras). A similar approach that employs RL-based approach for control policy search can also be found in Ref. [34].
From the literature review, it can be concluded that deploying state-of-the-art autonomous capabilities to a mobile robot usually entails developing complex NN-based architectures and training them on large data-sets (either in a simulation or in a real-world environment). If a different behavior is required, a new network needs to be developed or existing one retrained (and new training data generated/recorded). In order to avoid this, we propose the implementation of a mediator which would enable fusion of control signals from several sources (including, but not limited to, NNs). One possible function on which adaptive control in mobile robot navigation tasks could be based is collision probability (CP) [35] since obstacle avoidance usually has the highest priority in the navigation stack hierarchy. The mediation can be implemented in several forms, and one of them is based on fuzzy set theory [36]. It is worth noting that several mediation engines can be used in the process, as well as several decision functions based on which the mediator infers the final decision and thus adapts the robot's behavior [18].
Finally, it is worth noting that the implementation of ensembles of NNs is not a new idea. In Ref. [37] they were used in conjunction with a plurality consensus scheme for classification applications, with focus on optimizing NN parameters and architectures. The approach was tested in two (simple) scenarios: generalized exclusive disjunction (XOR) operator and region classification in the 20-dimensional hypercube. While the obtained results were an improvement over single copy networks, they are applicable only to NNs (i.e., no other algorithm can be introduced into the approach). There have also been approaches that utilize a single DNN for object detection, decision-making and inferring control commands [38], inspired by the way a human brain works. While this work focuses on robotic applications (using RGB-D camera as main sensors) and presents promising real-world results for indoor robot exploration tasks (including obstacle avoidance), it has two potential drawbacks: as Ref. [38] it is intended only for NN-based strategies, and since it uses CNNs it requires large amounts of data for training (which were recorded with human driver exploring an environment). Additionally, the use of fuzzy logic variants (e.g., fuzzy integral) for fusing outputs from several NNs has also been proposed before in Ref. [39] (for dynamic nonlinear process modelling) and Ref. [17] (for robust character classification purposes). However, in Ref. [17] nonadaptive fusion mechanism was used (i.e., the contribution of each network was known in advance based on its loss function). This is not suitable for intended application where, due to the dynamic nature of the environment, different controllers can have variable importance. Also, the approach (as is the case in Ref. [39]) does not consider a way to include other types of controllers (than NNs) or human input. Some work has been done on adapting the fusion scheme, like in Ref. [40] but without the use of fuzzy-based logic, using gating network that makes a stochastic one-out-of-n decision about which single network to use for a particular instance. The approach was tested in a multispeaker vowel recognition task. Also, as can be seen from the above discussion, in many such examples primarily intended application is not related to the field of robotics.
1.2 Contributions
The goal of the research was to develop a procedure to combine together outputs from two control algorithms (including NNs), each performing different task primitive in robot navigation. Fuzzy logic based mediation was chosen as a good framework since it: (a) enables combining individual controller outputs in a complex signal. In the process, different kernel functions (mediation engines) can be used to obtain different data fusion results., (b) its functionality is transparent and can be easily understood by an average user. Additionally, it has low computational complexity, making real-time implementation possible, and (c) depending on the global task, the decision (adaptation) variable can be freely chosen while maintaining generality of the framework and ensuring different behavior profiles.
Our contributions are thus as follows:
To the best of our knowledge, this is the first real-world application of fuzzy-based mediator for robot navigation-based tasks to date.
Development of NN-based obstacle avoidance and navigation entirely in simulation using LiDAR measurements (and not camera data, as is often done in the literature) and application of it in real-world navigation tasks without any modification (retraining) with good results. The approach provides both positive and negative examples and is self-contained since minimal human intervention is needed (e.g., specifying simulation environment parameters) during training data gathering and subsequent NN training.
Comparison of performance in different tasks and on different robots (with different footprints) which goes to the generality of the proposed approach.
Implementation of the mediation scheme in the teleoperation control for fusion between the obstacle avoidance controller and human operator. In this manner, a seamless control handover between the human operator and autonomous part of the robot is achieved ensuring safe movement of the robot in the environment where the human operator does not necessarily always have knowledge of all obstacles in the space (i.e., lower spatial awareness).
The remainder of the article is structured as follows. In Section 2, main operational principles of our approach are presented and discussed, while in Section 3 experimental setups for all test cases are presented with explanations for made design decisions and used algorithms. Section 4 presents achieved results using previously described experimental setups, as well as analyses and discusses the results. It also provides a comparison with a standard approach in the robotics. Finally, Section 5 concludes the article with the highlight of the main research findings, as well as proposed possible improvements and future research directions.
2. THE PROPOSED ADAPTIVE FUZZY MEDIATOR FOR MOBILE ROBOTICS
Overview of the proposed adaptive fuzzy control scheme can be seen in Figure 1 which shows that the approach uses two controllers (NNs or any other type of controller) whose inputs are combined together within fuzzy set theory based on CP (
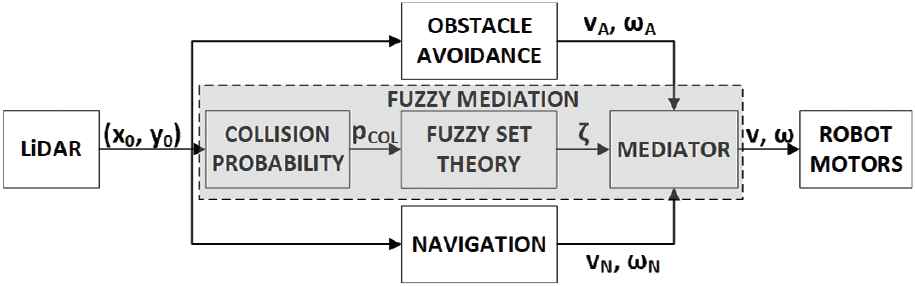
The general control architecture of the proposed approach.
In the proposed approach, one controller was used for reaching the goal position without regard to obstacles (navigation controller), while the other controller was used solely for obstacle avoidance without regard to the goal position. Both controllers (in the case of NN) were trained using data obtained in simulation, which made the proposed approach simple and safe.
NN-based obstacle avoidance consisted of three sub-NNs (left, right and forward). In order to train them, a simulation environment was created with a number of obstacles of various shapes and sizes scattered randomly within it. Then, a robot was spawned in its center with random orientation and was given a constant linear velocity and kept moving until hitting an obstacle (thus providing both positive and negative samples). A similar approach was used in Ref. [28]. While in motion, LiDAR collected data of nearby obstacles (
Equation (1) was implemented only if
In the case of the development of NN for navigation, the following procedure was taken. First, a single user was asked to drive a Turtlebot 2 mobile robot in Gazebo simulation from a random starting point to a random goal within a
Additionally, when a simple Proportional (P)-type controller was used, its output was such that it kept the linear velocity (
The outputs from NN-based obstacle controller and from navigation controller (being either NN or P-type) were then fed to the fuzzy mediation block, where the consensus decision was made (based on
CP was calculated in several simple steps as described hereon. First, an estimated trajectory of the robot for the next 20 samples (about 2 seconds) was computed based on a simple kinematic model of motion. The interval of
After the projected trajectory has been calculated, an uncertainty ellipse is constructed for each point on the trajectory. The ellipses have increasing axes lengths with each ahead sample in order to account for motion uncertainty. While this always positive increase might be considered too cautious in some instances (e.g., driving parallel with an obstacle/wall), we believe it is a prudent step since, in general, such situations where robots drive perfectly parallel with an obstacle are not too common. Also, with the appropriate selection of the initial ellipse dimensions as well as their increments (in respect to the distance used in NN obstacle avoidance training) this should not pose a serious limitation on robot performance (i.e., robot trajectory might be slightly longer, but the final objective would still be achieved). Ellipses’ initial axes lengths and increments were determined experimentally but may change if the situation warrants it. For example, during the testing with Turtlebot 2 mobile robot, the following ellipse parameters values were used:
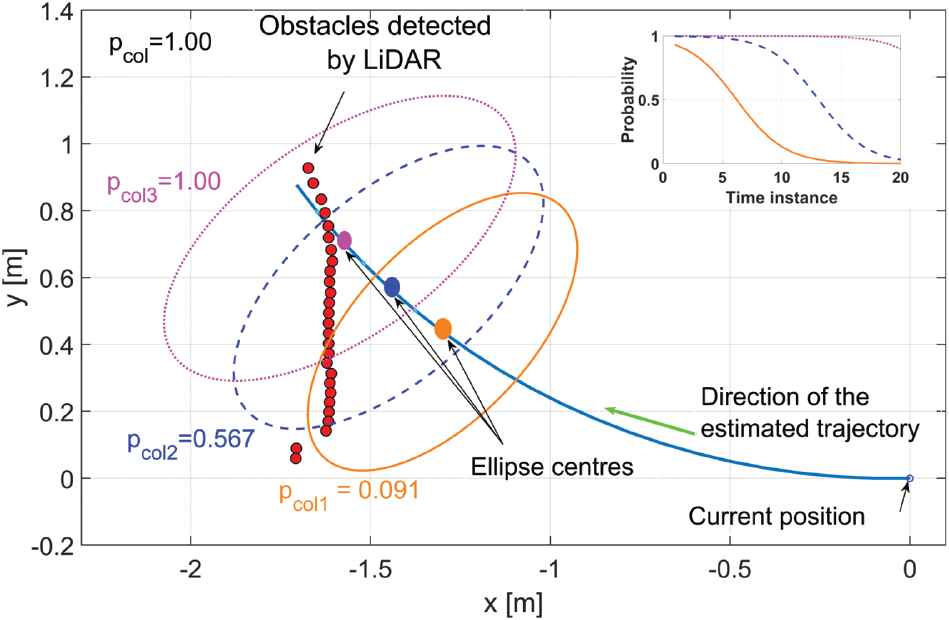
An example of collision probability (CP) calculation based on Light Detection and Ranging (LiDAR) data.
Once estimated trajectory and uncertainty ellipses are constructed, in the next step, each ellipse is examined in order to find if any (parts) of obstacles (i.e., LiDAR points) are located within it. If they are, the ellipse is considered further or is otherwise discarded. Then, for each remaining ellipse, a CP is estimated using a sigmoid function with variable parameters (depending on distance to obstacle and distance in estimation time horizon). An example of sigmoid functions is included in Figure 2.
The general sigmoid function that was used in the work for calculation of CP for time instance
Finally, when all CP values are calculated, the highest CP is kept for that time instance. It is then used for the mediator block as the decision variable (
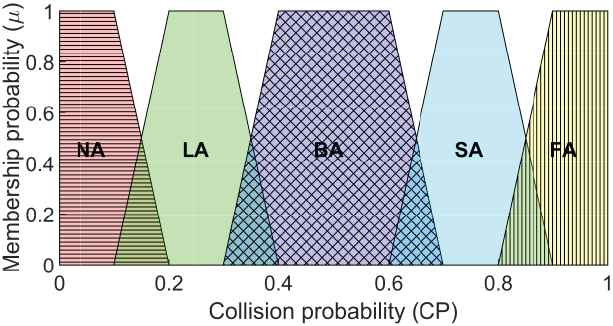
The fuzzy set membership function used in the calculation of mediation coefficient
Each of previously mentioned sets has its own control shift factor associated with it, which is then used to compute final output: 0, 0.25, 0.5, 0.75, and 1, respectively. This implies that the used mediation had a linear mediation engine, but other mediation engines (like exponential ones) can be used as is pointed out in Ref. [18]. Thus, the shift percentage is computed as
It was observed during the experimentation that coefficients used in Equation (5) dominantly depend on robots maximal allowed linear and angular velocities (and not the robot itself, although robot footprint was taken into account with LiDAR adjustments as described previously). As a side note, please note that in Equation (5), calculated CP value could potentially be directly used for thresholding (circumventing fuzzy set approach), but in practical testing this proved to be too sensitive to estimated trajectory changes (uncertainties). Additionally, since CP does not need to be used as a decision variable (e.g., when a different task is considered) removing fuzzy set would reduce generality of the proposed approach, as well as possibility of using nonlinear control shift functions.
In Equation (6)
Here we demonstrate the whole calculation procedure on a simple example. Lets assume that the robot is going toward the goal point with linear velocity of
3. EXPERIMENTAL SETUP
The experimental verification and testing of the proposed approach consisted of three main parts: simulation-based one (Subsection 3.1), real-world-based one (Subsection 3.2), and application-specific one (Subsection 3.3). The main idea behind each of them was as follows. The goal of simulation experiment was to initially verify the functioning and viability of the proposed approach, while the goal of the real-world experiment was to build-upon simulation experiment and demonstrate that the approach is valid on real robots with different footprints and in different (realistic) situations. Finally, the application-specific testing had the goal of demonstrating that the proposed approach could be of practical use for solving or at least minimizing some of the real-world problems (teleoperation was chosen as one such problem). In all three cases, NNs used for the obstacle avoidance (as described in more detail in Section 2) were trained and deployed using TensorFlow open source machine learning framework (on top of Keras). Same machine learning framework was used for training and deploying NN navigation controller. These networks, along with other controller(s), mediation and all other algorithms were deployed in ROS environment which enabled us (in some cases) to run the system in a distributed manner (i.e., NN was running on a separate computer due to hardware requirements related to TensorFlow).
3.1. Simulation
Simulation experiments were carried out in Gazebo 7 simulation environment. A random environment was generated during this test, with randomly distributed obstacles of different shapes (cylinder of
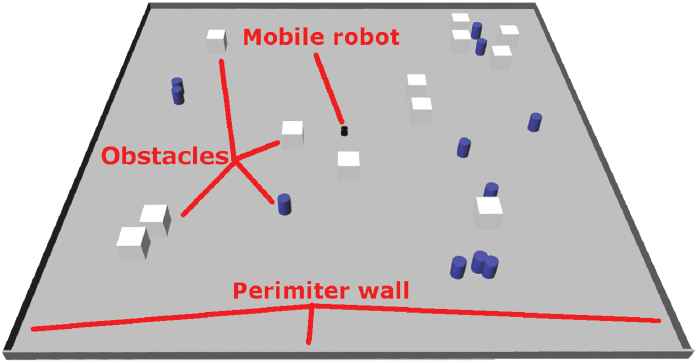
Example of Gazebo simulation environment used for initial testing of the proposed approach.
The random environment generated during the testing had a fixed size (defined by a perimeter wall) of
3.2. Simple Real-World Scenarios
Real-world experiments were carried in the indoor environment at Faculty of Electrical Engineering, Mechanical Engineering, and Naval Architecture, University of Split. During the experiments, two mobile robot platforms with very different footprints and characteristics were used: customized Turtlebot 2 depicted in Figure 5, and a custom-built mobile platform intended to be used as an automated pallet carrier depicted in Figure 6. Please note that in the case of a custom-built robot raw LiDAR data was not fed to the NN obstacle avoidance but rather an adjusted one. The adjustment was achieved by simply adding/subtracting from the measured distance (in an on-line manner) which took into account robot footprint and sensor placement within it, so to be in line with the one used for NN training. If training was achieved with a different/actual footprint this step would not be needed, but nevertheless, it shows how the approach can be expanded to work with different robots.
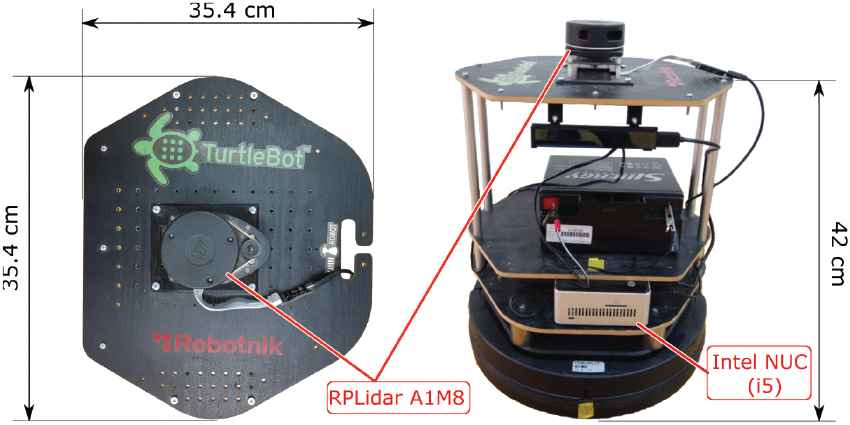
Overview of customized Turtlebot 2 mobile robot platform. Please note that the robot (with the battery) weights around 10 kg.
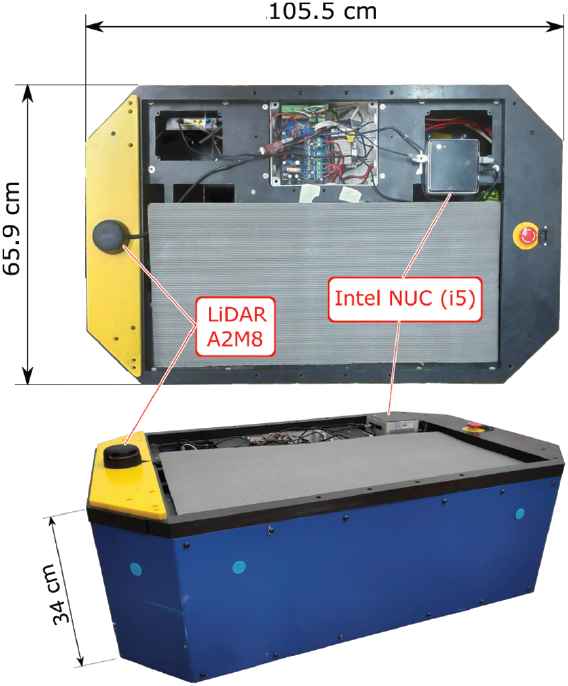
Overview of a custom-built robot platform (the robot was built by our partner Statim d.o.o.). Please note that the robot has a weight of about 100 kg.
The main idea behind the use of such different mobile bases was to demonstrate the effectiveness and generalization of our mediation approach. This was important, since a number of parameters are needed for the approach (as described in Section 2), and the question of generality (i.e., the need for fine-tuning them) naturally arises. As will be discussed later on in Section 4.2 it was found it is sufficient to fine-tune only two parameters (related to uncertainty ellipses) to ensure the desired behavior of the mobile robot. Fine-tuning other parameters could possibly improve the performance, but optimisation was not in the research focus.
Next, two main test scenarios were devised for each of the mobile bases. First, for the Turtlebot 2, the experiments consisted of three distinct navigation and obstacle avoidance tasks. In all three cases, three setups were used: proposed approach with NN navigation and with P controller navigation (both with NN-based obstacle avoidance), as well as default ROS navigation stack with DWA as a baseline method. First two tasks were conducted in an environment augmented with Z- and U-shaped (convex dead-end) obstacles. Five instances of these tasks were run per each setup (
3.3. Teleoperation Scenario
The purpose of the final test was to demonstrate the practical applicability of the proposed approach. Thus a simple teleoperation scenario was envisaged in which users had to avoid a single obstacle and reach a goal point. Teleoperation was chosen since it lends itself as a natural testing ground for automatic obstacle avoidance and human–robot interaction approaches. An overview of this simple experimental setup is depicted in Figure 7.

Overview of a simple teleoperation scenario used in the experiment.
Total of
Did you feel in full control during the teleoperation?
Do you feel that automatic obstacle avoidance through mediation helped you during teleoperation?
Was completing the required task easier with or without the mediation?
Answers for the first two questions were on a Likert-like scale with three labelled answers (e.g., “Strongly agree,” “Neutral,” and “Strongly disagree”) and the continuous line between them. The users had to mark a place on the line which best matched their response. This, in turn, enabled us to obtain continuous variable data from the responses. Please note that the users were not allowed to practice the mediated teleoperation so that they would not get accustomed to it. They were, however, free to test the remote controller and video feedback. Results for this experiment are presented in Section 4.3.
4. RESULTS AND DISCUSSION
The results reported throughout Section 4 are summarized in Table 1 for easier reading. They will be explained in more detail in the following subsections. Please note the bottom row pertaining to total distance covered during reported testing, as well as the time and number of instances tested. This is indicative of the extent to which the proposed approach was tested (keep in mind when interpreting the results this was all indoor testing).
| Env. | Robot | Scenario | Controller setupa | ADT |
ATT |
Trials |
|---|---|---|---|---|---|---|
| Simulation | Turtlebot 2 | Obstacle course | NN/NN | 13.08 |
68.8 |
15 each |
| NN/P | 7.44 |
38.4 |
||||
| NN/NN | 8.75 |
43.76 |
||||
| Z-shaped obstacle | NN/P | 8.20 |
46.32 |
5 each | ||
| DWA/ROS | 9.80 |
37.91 |
||||
| NN/NN | 12.25 |
69.15 |
||||
| Turtlebot 2 | U-shaped obstacle | NN/P | 12.66 |
73.06 |
5 each | |
| DWA/ROS | 7.64 |
39.61 |
||||
| NN/NN | 51.11 |
316.78 |
||||
| Real-world | Navigation | NN/P | 75.76 |
466.55 |
2 each | |
| DWA/ROS | 47.41 |
245.50 |
||||
| NN/NN | 13.37 |
73 |
||||
| Obstacle course | NN/P | 12.39 |
68.33 |
3 each | ||
| DWA/ROS | 13.93 |
110.33 |
||||
| Custom built | NN/NN | 47.55 |
301.5 |
|||
| Navigation | NN/P | 53.11 |
403.60 |
2 each | ||
| DWA/ROS | 47.51 |
223.5 |
||||
| NN/line following | 49.31 |
288 |
||||
| TOTAL | 1,466.78 (78.27%b) | 8,401.29 (80.28%b) | 83 (79.52%b) |
Env. = Environment; ADT = Average Distance Travelled; ATT = Average Time Taken; STD = Standard Deviation; DWA= Dynamic Window Approach; NN =neural network; ROS = Robot Operating System.
obstacle avoidance controller type / navigation controller type.
percentage of total value recorded during testing of the proposed method (i.e., not including the baseline method).
Summary of experimental results.
4.1. Simulation
Example trajectories (random
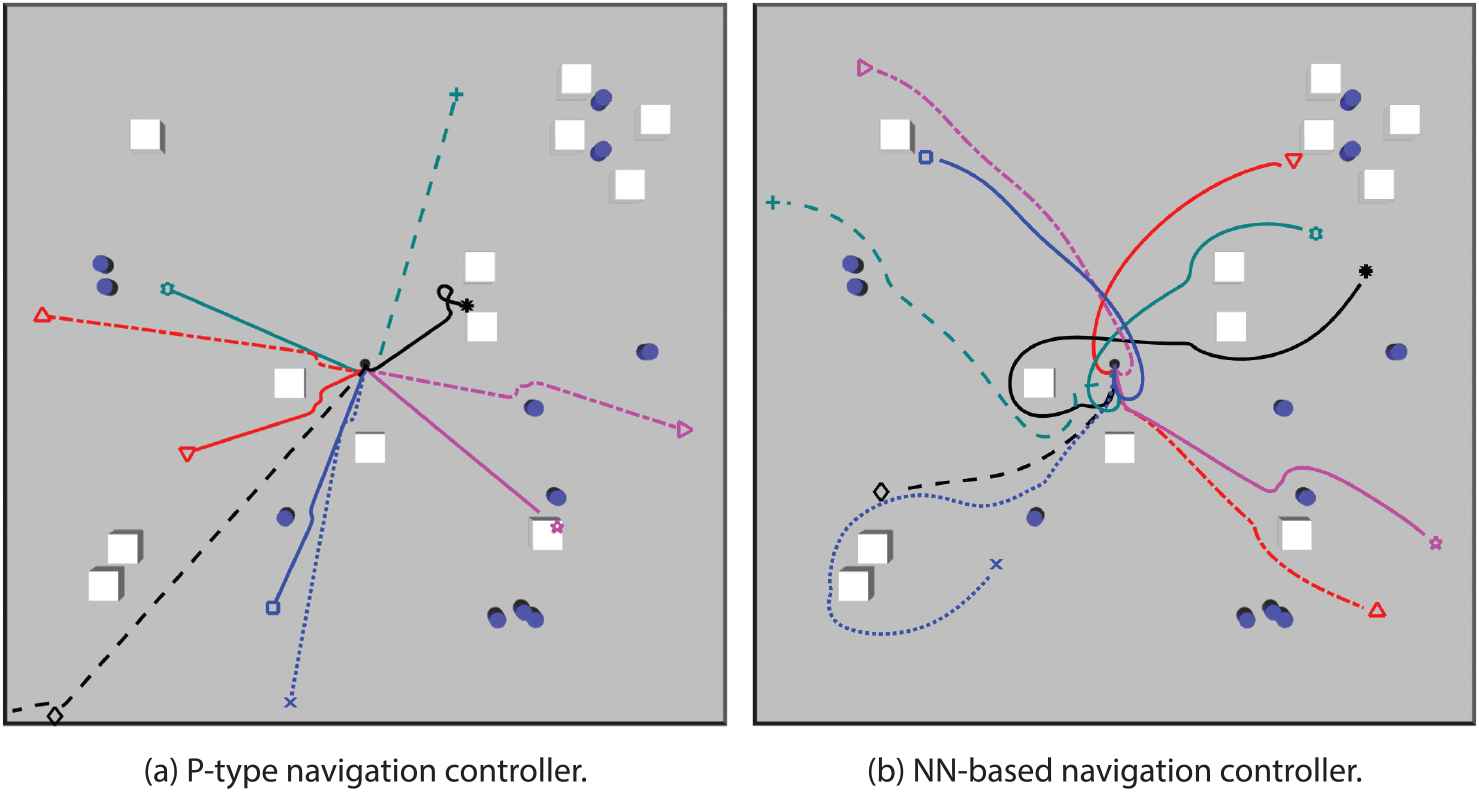
Trajectories acquired during testing mediation in a simulation environment using Turtlebot 2 model. Please note that goal points are marked with different symbols.
It is worth noting that for NN-based navigation controller the mobile base never crashed, while for the P-type based navigation controller in four cases (
Looking at the presented trajectories in Figure 8 several interesting observations can be made. First, it is clear that P-type controller results in a more direct approach to the goal (i.e., “aggressive” nature mentioned before), while the NN-based navigation takes a more circular trajectory even when the goal is in the line of sight with no obstacles in-between. From Figure 8a it can also be observed that when the goal is too close to the obstacle (trajectory with the dark dashed line and circle goal marker) the robot might not reach its intended goal (since mediation algorithm switches it to obstacle avoidance). Some improvement might be possible here if adaptive CP calculation is employed using remaining distance to the goal as well as adaptive robot speed (but obviously there is a limit to this approach). Next, when the goal is placed within the obstacle (especially if it is within a corner type environment - dark full line trajectory with pentagram goal marker) the crash is inevitable since the obstacle avoidance does not react appropriately (there is no stop-and-turn in-place mechanism). This, however, does not in our view represent the failure of the proposed fuzzy mediation approach (since it worked as intended) but highlights shortcomings of the developed obstacle avoidance approach (and ways of improving it, e.g., in-place rotation). Finally, if the target is close to the obstacle, but still far enough so that obstacle avoidance is not activated (dark full line trajectory with full circle goal marker), it might take a while for a robot to reach the goal (switching several times between navigation and obstacle avoidance controller - note the end part of the trajectory), but it will reach it. Looking more closely at the Figure. 8b it can be seen once more that the robot does not take the most direct route in NN-based navigation and that obstacles sometimes interfere with the navigation (i.e., trigger the obstacle avoidance) as depicted by dark full line trajectory with asterisk goal marker and dark dotted trajectory with x goal marker. This extends distance travelled, but the robot ultimately reaches its goal, even when the goal point is close to the obstacle (trajectories with a full dark line and triangle end marker and full dark line with square end marker).
Despite several crashes, and based on the above discussion, we concluded that the proposed fuzzy mediation algorithm is a viable algorithm and it performed as expected in the simulation. Thus, we were encouraged to deploy it in real-world scenarios and on real mobile robots. It should be noted that during the transfer no additional re-training of the NNs was performed (i.e., they were fully trained in simulation).
4.2. Simple Real-World Scenarios
As was explained in Section 3.2 first real-world testing was carried out using modified Turtlebot 2 mobile robot in case of Z- and U-shaped obstacles. Example of obtained trajectories for one random case per setup can be seen in Figure 9 along with associated CP and mediation coefficients.
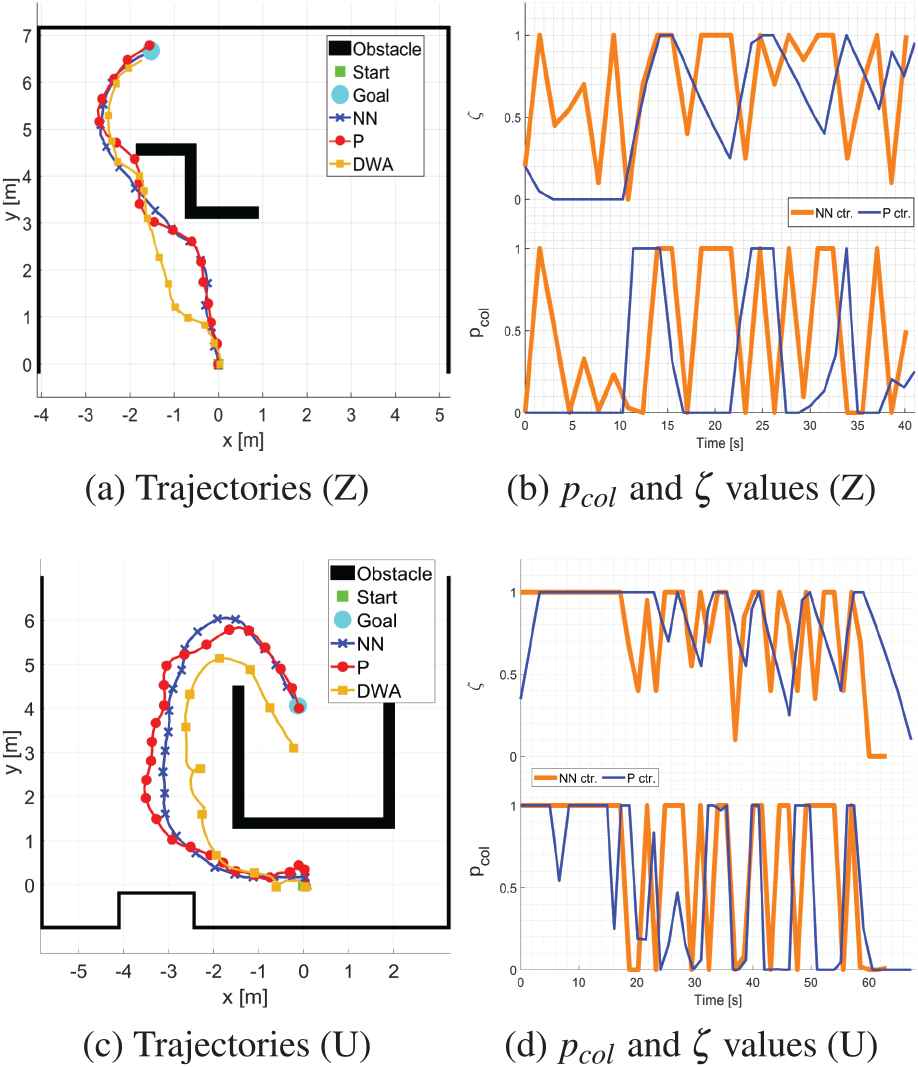
Examples of simple navigation task results with U- and Z-shaped obstacles.
The figure shows that for all three used setups the robot reached goal area (there is a small error for DWA end position, but we contribute this to AMCL/encoder related issues in the recorded data, since the physical robot reached the target). As expected, DWA reached the goal in a more direct trajectory in both cases, while the proposed approach had a few direction changes due to the fusion of navigation and obstacle avoidance parts. Here, again a more “aggressive” nature of the P-type controller is seen: there are more direction changes in its trajectory than in a case of NN driven navigation which is smoother. However, in all particular cases, the proposed mediation algorithm performed as expected, enabling the robot to execute a simple navigation task.
It is interesting to note that DWA also had some issues with U-shaped obstacles. This resulted in longer navigation run than in both setups for the proposed approach (
The change in CP and
Next, a more demanding navigation task was used for the Trutlebot 2 robot. Examples of the obtained trajectories (for two different goal points) are depicted in Figure 10. Please note that although obtained trajectories are plotted on the map, the robot itself does not have access to the map in the proposed approach (but does have it, without the obstacles, for ROS/DWA case). In essence, the robot path planning is a straight line, going from start to the goal position in the proposed approach. From the figure, it can be observed that robot successfully reached given goals in all cases, with ROS/DWA again having a more direct route which is reflected in completion times in Table 1. The main reason for this is that (upper) corridor in which robot had to enter was narrow (
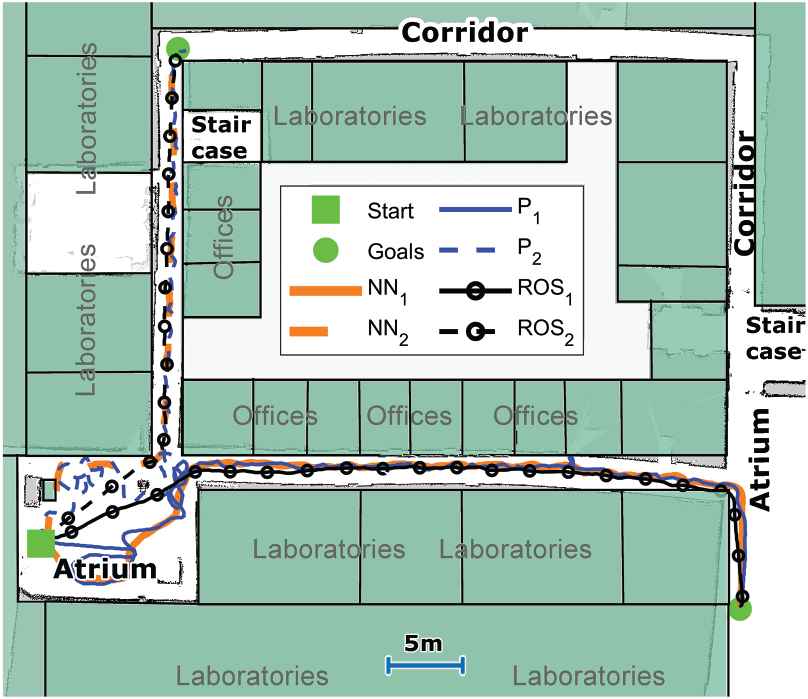
Examples of navigation trajectories for a realistic environment. A map depicts part of the 4th floor at authors’ home institution (overlaid over robot generated map using Robot Operating System [ROS] gmapping package).
In the next stage of testing a larger (custom built) robot with different footprint was used. It was first tested on a larger obstacle course where it had to go from start to a goal position. The experimental setup and the obtained trajectories are presented in Figure 12 and results summarized in Table 1.
From the results, it can be seen that the robot successfully (i.e., without the crash) completed the task in all test cases (please note again that in mediation cases the robot did not have access to the map, while for ROS/DWA it had but without obstacles in it). As in all cases before, the ROS/DWA seems to have a more direct trajectory. This is however misleading since this approach had, in all cases, number of in-place turns (which are not visible in the figure, but are reflected in time results in Table 1) and even some backward driving (as seen in the figure as a bottom dotted dark line trajectory). This is confirmed when completion times are examined (for goal points from top to bottom): NN navigation had times of
As the final test, a more complex navigation task with the custom-built robot was introduced. The environment was the same as in the complex navigation task of Turtlebot 2. Obtained results are depicted in Figure 11.
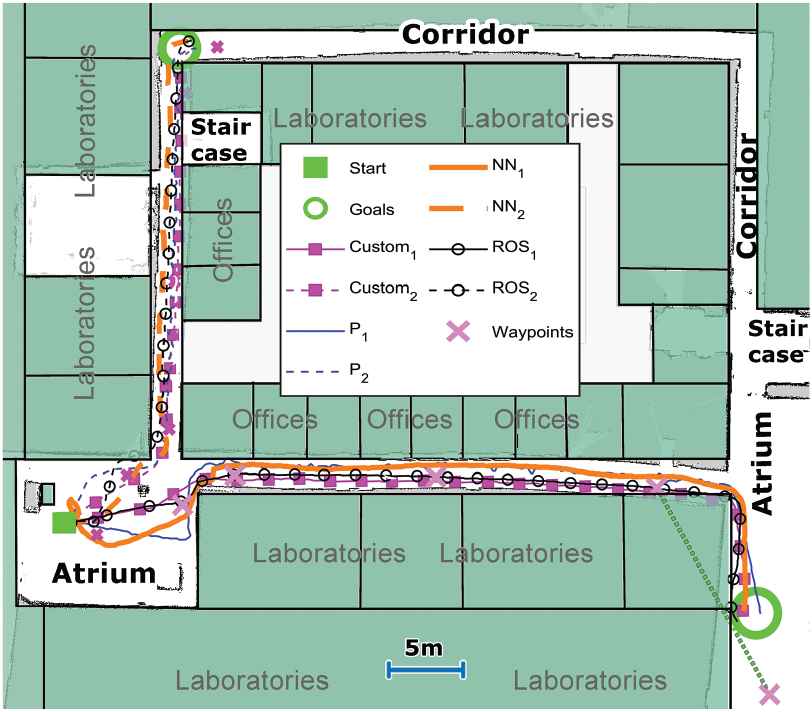
Examples of navigation trajectories for a realistic environment using a custom-built mobile robot platform. A map depicts part of the 4th floor at authors’ home institution (overlaid over robot generated map using Robot Operating System [ROS] gmapping package).
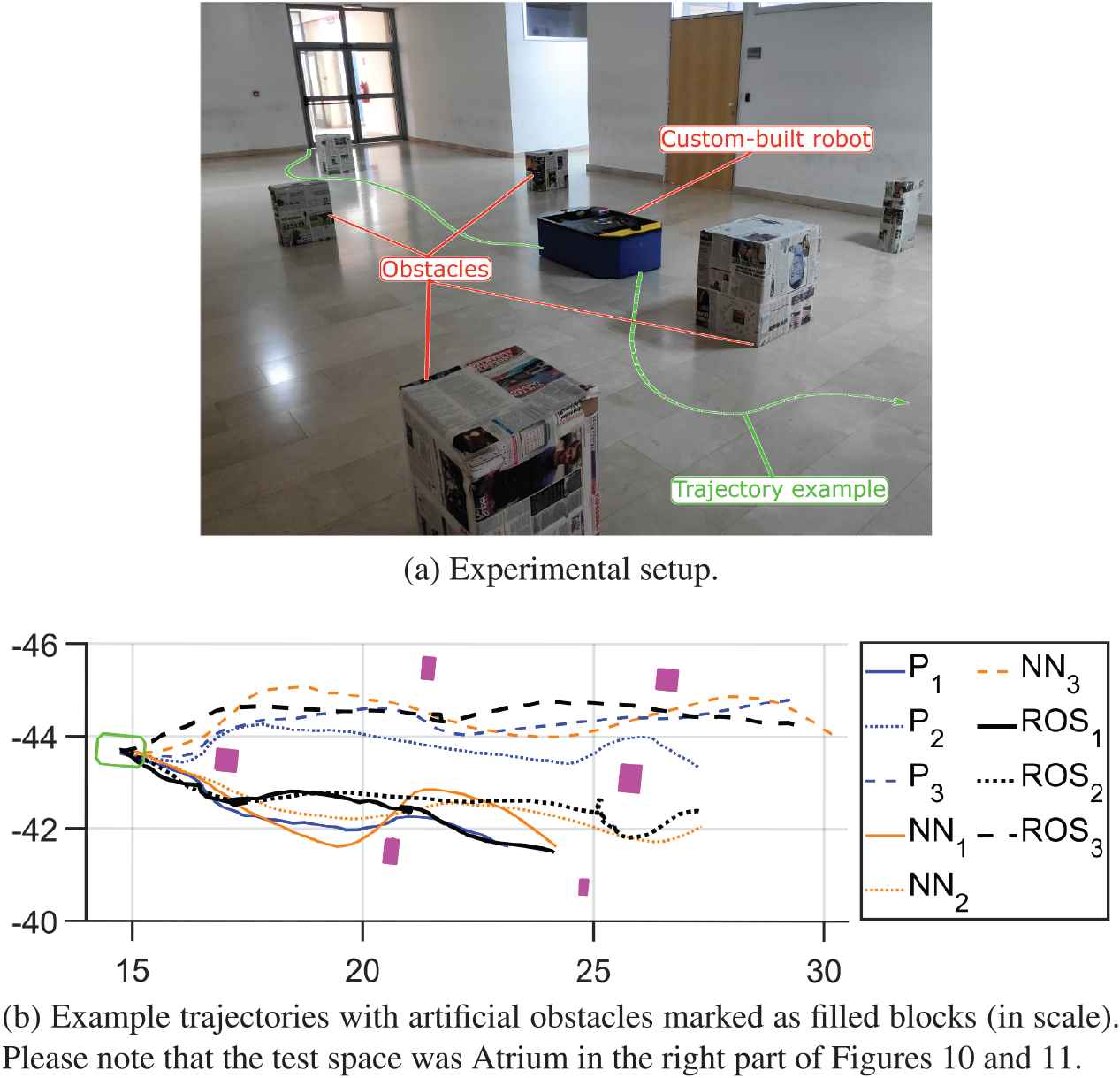
Experimental measurement with the custom-built robot on an obstacle course.
From the trajectories presented in the figure, it is clear that in all cases the robot successfully completed the given task. However, the manner in which it was completed was slightly different, especially for the P-type navigation controller. To be more precise, the mobile robot, in that case, took numerous direction corrections (as can be seen best from thin solid dark line trajectory) due to the fact that it aggressively changed its direction, and due to robot's larger dimensions in relation to corridor width, thus often engaged obstacle avoidance. This behavior was not detected in the case of NN-based navigation, where the trajectory was smoother. It should be noted that even ROS navigation stack with DWA had several in turn rotations when coming into the narrow corridors. If completion times are examined the following values are obtained (to the first and the second goal point respectively). The P-type controller finished the course in
4.3. Teleoperation Scenario
During the application-based testing, users in all test cases successfully completed the given task. In
Looking at the responses for the first two questions of the mini-survey which test subject completed after finishing the experiment, the following results were obtained. For the question Did you feel in full control during the teleoperation? the mean response had a value of
Based on the obtained results from the mini-study we can conclude that in general users found the approach to be helpful and felt that they were in the control of a robot (results which might have been slightly better if feedback about mediation status was provided). However, due to the small sample size used and simple tasks given, further analysis is needed to make definite conclusions on the impact of the fuzzy mediation in the teleoperation scenario. Nevertheless, the results are encouraging and they demonstrate the viability of the proposed fuzzy mediation approach in practical real-world problems.
5 CONCLUSIONS
The paper presents an idea of fuzzy-based mediation for (simple) mobile robot navigation tasks and implements it on a couple of real robots. It combines the outputs of two controllers, one dedicated to navigation to the goal point and the other for obstacle avoidance, to the final output which is (in general) a combination of the outputs of the two controllers. The approach is thoroughly tested, both in simulation and in real-world scenarios, using two mobile robots of different architecture, footprint sizes and shapes.
While it was previously shown that NN can be used to solve robot navigation task and obstacle avoidance task separately, the experiments in the paper demonstrate that the problem can be broken down into task primitives (with or without the use of NNs) with the application of adaptive fuzzy mediation, thus adapting robot behavior. The NN ensembles approach for fusing the output of two or more NNs has been demonstrated before, but what the proposed approach enables is a more transparent manner in which this is done and which can be fine-tuned intuitively to adaptively change. Also, it is not limited only to NN-based controllers, but other controllers like PID controller can be used. In this manner, more complex behavior can be achieved by combining task primitives while enabling modularity, that is, controllers addressing certain task can be changed, without influencing other task controllers.
Obtained results demonstrate that the inclusion of different types of controllers (while keeping the mediation mechanism unchanged) is possible, which opens up additional possibilities for adaptation and optimisation. Although results show good performance (especially in realistic tasks), comparison to a baseline method shows some differences (in general slower completion time and longer distance travelled, although there were some cases where the proposed approach was on average faster and with shorter trajectory length), but overall performance is satisfactory (and without any human intervention). However, there are some issues that should be noted. First, there were situations (in terms of obstacle shape and relative start-goal relation) with the proposed approach which resulted in robot getting stuck in the infinite loop type behavior (e.g., if the robot is placed deep inside U-shape obstacle and needs to go to start point as its goal point as depicted in Figure 9). This issue with a similar approach was also noted in Ref. [20]. We believe this could be addressed with RL or inclusion of automatically generated virtual way-points in cases when looping is detected. The second thing to note is that there were more crashes with the proposed approach than with the baseline algorithm (ROS/DWA). While this is certainly undesired behavior, it happened in a subset of events where the proposed fuzzy mediation worked as expected, but NN-based obstacle avoidance was simply not up to the task. The issue could be resolved, or at least reduced, by a better trained NN obstacle avoidance controller (or other type of controller) or by fine-tuning the mediator algorithm (e.g., faster hand-off to the obstacle avoidance, or CP calculation further in time although this would have a limited effect since the hand-off would be made earlier, but current NN would not react in time since it was trained for 1 m distance). Thirdly, some minor parameter tuning had to be done after transferring the algorithm to a mobile robot with a different footprint, but the same had to be done for a baseline algorithm (ROS/DWA) as well. This could also be potentially addressed by an adaptive change of parameters, but we believe that ultimately certain engagement by a human operator in the tuning process will still be needed.
The possible improvements (and our future research directions) include the following: adaptive change of algorithm's parameters based on robot footprint and sensor placement, inclusion of better trained NNs and/or NNs with different architecture like RNNs, NNs capable of reliably avoiding dynamic obstacles, fuzzy set approach in obstacle avoidance NNs for switching between left and right turns, testing with nonlinear mediation engines, inclusion of other types of controllers as well as testing with other task primitives, developing the approach to accommodate more than two controllers, and testing on additional robots and in more complex teleoperation scenarios. Finally, we plan to implement a simulation-based tool for testing and fine-tuning parameter values used in the approach for different environments, robot setups, and requirements.
CONFLICT OF INTEREST
The authors declare that there is no conflicts of interests.
AUTHORS' CONTRIBUTIONS
J.M. and S.K. conceived the research idea as well as experimental design. They carried out data acquisition, and participated in data analysis and manuscript preparation. I.S. and V.P. participated in data analysis and interpretation, as well as manuscript preparation, providing critical feedback that helped shape the research and the manuscript.
Funding Statement
This research has been partially supported by the Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, University of Split through project “Computer Intelligence in Recognition and Support of Human Activities”.
ACKNOWLEDGMENTS
Authors would like to express gratitude to the company “Statim d.o.o.”, for providing/loaning one of the robots (depicted in Figure 6) used in the experimental testing. Authors would also like to thank to all the students and the Faculty staff who took part in the teleoperation study.
REFERENCES
Cite this article
TY - JOUR AU - Josip Musić AU - Stanko Kružić AU - Ivo Stančić AU - Vladan Papić PY - 2019 DA - 2019/10/14 TI - Adaptive Fuzzy Mediation for Multimodal Control of Mobile Robots in Navigation-Based Tasks JO - International Journal of Computational Intelligence Systems SP - 1197 EP - 1211 VL - 12 IS - 2 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.190930.001 DO - 10.2991/ijcis.d.190930.001 ID - Musić2019 ER -
