Effective Channel Order Determination Algorithm for Convolutive Blind Channel Identification
- DOI
- 10.2991/ijcis.d.190819.001How to use a DOI?
- Keywords
- Effective channel order determination; Numerical analysis arguments; Blind channel identification; Higher-order cumulant tensor
- Abstract
Effective channel order determination is an important problem in convolutive blind channel identification. The classical techniques are based on information theoretic criteria, which show a great potentiality to estimate the effective channel order. However, these methods are just effective for the overdetermined case, i.e., the number of sensors is larger than the number of source signals. When the number of sensors is less than or equal to the number of source signals, i.e., in the underdetermined or determined case, it is difficult to detect the effective channel order. In this paper, an improved algorithm is proposed to estimate the effective channel order by integrating numerical analysis arguments and higher-order cumulant tensor. In the proposed algorithm, we exploit the information contained in the higher-order data statistics and rearrange the tensor as a matrix using the unfolding operation, then utilize the eigenvalues of the matrix and combine numerical analysis arguments to detect the effective channel order. Finally, a series of experiment results demonstrate the effectiveness and superiority of the proposed algorithm.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
It is well known that a key issue is the determination of effective channel order in convolutive blind channel identification [1–3]. A common assumption in some papers [4,5] is that the effective channel order is known. However, in practice, it is unknown and has an important effect on the channel identification. Especially, in the underdetermined convolutive mixture model [6–8], it is a difficult issue due to the complexity of the model. Therefore, the effective channel order determination is a challenging problem to be solved in the blind channel identification.
Among numerous methods, the information theoretic criteria have become the classical techniques [9,10], such as Bayesian information criterion (BIC) [11], generalized information criterion [12], the model selection introduced by Akaike information criterion (AIC) [13], by Schwartz and Rissanen minimum description length (MDL) [14,15], a method with the random matrix theory (RMT) algorithm [16], the automatic order selection [17], N-way probabilistic clustering [18,19]. In addition, an effective method has been proposed based on numerical analysis arguments [20,21], which detects the effective channel order using a rank detection method to the single-input/multiple-output (SIMO) case. By using the concept of standard angle between subspace and invariant subspace perturbation results, the maximum stable decomposition from the range space of data covariance matrix to signal and noise subspace is provided. Moreover, the signal order estimation is also required in several applications of signal processing. For example, signal rank detection problem in cognitive radio and the source number determination in blind unmixing problems. However, these methods are just suit for the overdetermined case. For the underdetermined case, they have some limitations which may cause inaccuracy of the effective channel order estimation.
To compensate for previous shortcomings, the higher-order cumulant tensor methods [22–24] are capable of processing the underdetermined case, and blindly identify the steering vectors of up to
In this paper, an improved algorithm is proposed by combining numerical analysis arguments and higher-order cumulant tensor to deal with the detection problem of effective channel order in the convolutive blind channel identification. First, we provide a straightforward theoretical analysis to illustrate the effectiveness of the proposed algorithm. Especially, in the SIMO case, the improved algorithm directly provides the effective channel order determination. Second, for the underdetermined convolutive case, supposing the number of source signals is known, we exploit the information contained in the higher-order data statistics and rearrange the tensor as a matrix by using an unfolding operation, then utilize the eigenvalues of the matrix and combine numerical analysis arguments to estimate the effective channel order.
The contribution of this paper are as follows.
We propose an improved algorithm by integrating the merit of higher-order cumulant tensor and numerical analysis arguments to estimate the effective channel order for convolutive mixture model.
We employ higher-order cumulant tensor to solve the source number estimation for underdertermined linear mixture case. Meanwhile, the proposed algorithm can be directly used to detect the effective channel order for the SIMO convolutive mixture case. Experimental results demonstrate the effectiveness and superiority of the proposed algorithm.
The structure of the remaining of this paper is organized as follows. The system model statement and algorithm overview is presented in Section 2. Section 3 introduces the numerical analysis arguments and higher-order cumulant tensors. Experiment results are shown in Section 4. Finally, Section 5 summarizes the conclusion and future work.
Notations: In this paper,
2. SYSTEM MODEL AND ALGORITHM OVERVIEW
2.1. Convolutive Model
Consider
where
2.2. Algorithm Overview
We propose an improved algorithm to detect the effective channel order for convolutive blind channel identification. The block diagram of the proposed algorithm is shown in Figure 1. The processing is based on two-step method. In the first step, we exploit the information contained in the higher-order data statistics and rearrange the tensor as a matrix using the unfolding operation. Then we estimate the covariance matrix of the data, and compute the eigenvalues of the covariance matrix using eigenvalue decomposition. In the second step, we detect the effective channel order using numerical analysis arguments.

Block diagram of the proposed algorithm.
3. NUMERICAL ANALYSIS ARGUMENTS AND HIGH-ORDER CUMULANT TENSOR
3.1. Numerical Analysis Arguments
In the following, we consider the one-input/two-output case, the results can be extended to the multiple-input/multiple-output (MIMO) situation. We denote the impulse response of the
where
The additive channel noise is assumed with zero mean and unit variance, i.e.,
Therefore, the covariance matrix of
Denoting the eigenvalues of
The distance measure between two linear subspaces commonly used for numerical analysis is the sine of their standard angles.
where
Thus,
Then we have further that
If
Otherwise, our upper bound is equal to 1. Therefore, we obtain
If
Therefore, the effective channel order is detected by minimizing
3.2. Fourth-Order Cumulant Tensor
In the following, we use the multilinearity property of the fourth-order cumulant tensor and construct the canonical model as follows:
It is assumed that the kurtosis values of source signals are known, then the decomposition model can be written as [29–32]
In this paper, we use
Thus, the fourth-order statistics of the data are characterized by the
Then we calculate the eigenvalues of the matrix and combine numerical analysis arguments to estimate the effective channel order in the underdetermined case. It should be noted that if the number of source signals is much more than the number of sensors, fourth-order cumulant tensor method is not valid. For this reason, much more higher-order cumulant tensors need to be used.
3.3. Sixth-Order Cumulant Tensor
For the sake of convenience, we define the entries of the sixth-order cumulant tensor
Such components can be ordered in the hexacovariance matrix:
Thanks to the multilinearity property of higher-order cumulant tensors, which implies:

Proposed effective channel order determination algorithm.
4. SIMULATION RESULTS AND DISCUSSION
In this section, we first test the proposed method to estimate the number of source signals in the overdetermined and underdetermined linear instantaneous mixture case. Meanwhile, information theoretic criteria are used to compare with our proposed method. Then the proposed method is used to detect the effective channel order in the convolutive mixture case. Finally, experiment results in terms of the probability of correct detection are shown as the performance measure. Meanwhile, we consider the computational complexity of the proposed algorithm. All the simulation experiments are conducted on a computer with Inter (R) Core (TM) i5-2537M CPU @ 1.40GHz, 4.00 GB memory under Windows 7 operational system and the programs are coded by Matlab R2015b installed in a personal computer.
4.1. Source Number Estimation in Linear Instantaneous Mixture Case
We consider the received signals with noise as follows:
In the simulation, we can estimate
In the first experiment, we estimate the number of source signals in the linear instantaneous mixture model, and consider an array with six sensors

Detection of number of sources in overdetermined linear instantaneous mixture case with noise. (a) Information theoretic criteria. (b) Proposed method.
In the second experiment, we consider an array with six sensors

Detection of number of sources in underdetermined linear instantaneous mixture case with noise (a) Information theoretic criteria. (b) Proposed method.
Remark 1:
According to Figure 3, it is shown that both information theoretic criteria and the proposed method demonstrate the effectiveness to detect the number of source signals in the overdetermined case. However, in the underdetermined case, information theoretic criteria are invalid, our proposed algorithm shows the effectiveness and superiority according to Figure 4.
4.2. SIMO Convolutive Mixture Case
In the third experiment, we consider a SIMO convolutive mixture case, and select six sensors

Detection of effective channel order in single-input multiple-output (SIMO) convolutive mixture case. (a) Information theoretic criteria. (b) Proposed method.
4.3. MIMO Convolutive Mixture Case
In the fourth experiment, we consider a MIMO convolutive mixture case, and select five sensors

Detection of effective channel order in multiple-input multiple-output (MIMO) convolutive mixture case. (a) Information theoretic criteria. (b) Proposed method.
4.4. Underdetermined Convolutive Mixture Case
In the fifth experiment, we consider an underdetermined convolutive mixture case, and select seven sensors

Detection of effective channel order in underdetermined convolutive mixture case. (a) Information theoretic criteria. (b) Proposed method.
4.5. Results in Terms of the Probability of Correct Detection
In the following, we conduct simulations in terms of the probability of the correct detection (PoD), i.e.,
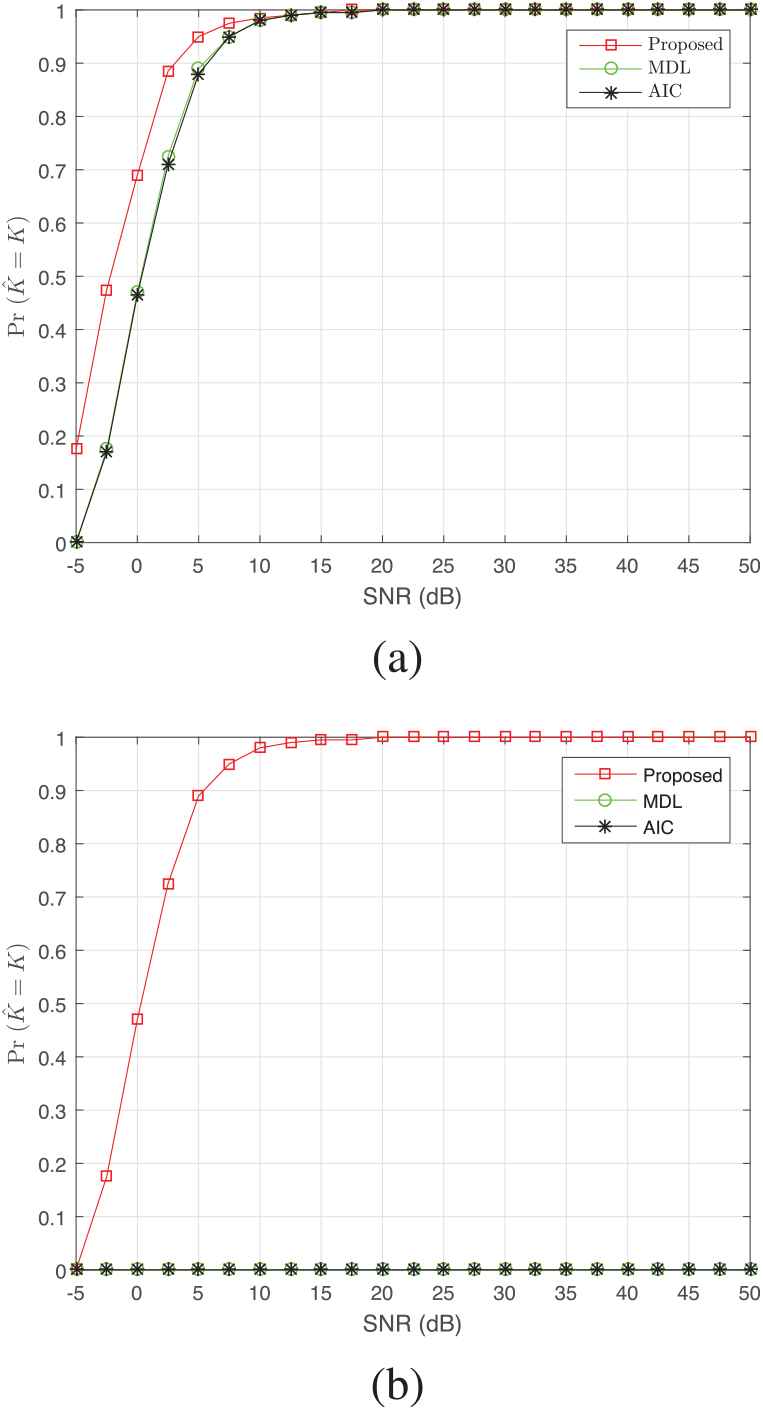
Results in terms of probability of the correct detection (PoD) versus (a) overdetermined convolutive mixture case, (b) underdetermined convolutive mixture case.
Remark 3:
According to Figure 8, it is shown that PoDs of all algorithms increase monotonically with SNR and attain 1 at SNR = 20dB. Therefore, we select SNR = 20dB as the fixed value. However, when the effective channel order is larger than the number of sensors, the information theoretic criteria are invalid. In this case, the proposed algorithm has superior performance compared with information theoretic criteria.
4.6. Computational Complexity of the Proposed Algorithm
Finally, we consider the computational complexity of the proposed algorithm. For high-order cumulant tensor algorithm, one of the most time-consuming calculations is the matrix–matrix multiplication. For example,

Running time of the proposed algorithm.
Additionally, we consider the comparisons between the fourth-order and sixth-order cumulant tensors. We select seven sensors

Detection of effective channel order in underdetermined convolutive mixture case. (a) Fourth-order cumulant tensors. (b) Sixth-order cumulant tensors.
5. CONCLUSION AND FUTURE WORK
In this paper, we provided an improved algorithm by integrating the numerical analysis arguments and higher-order cumulant tensor to detect the number of source signals and the effective channel order in the underdetermined convolutive mixture case. Especially, in the SIMO case, the effective channel order can be estimated directly. Furthermore, we obtain the relationship between the number of source signals and the effective channel order based on the experimental results. Finally, numerous simulation experiments demonstrate the effectiveness and reasonableness of the proposed algorithm.
In addition, some further research directions need to be considered. First of all, it is worth noting that the higher effective channel order is, the more higher-order cumulant tensors need to be used. However, it is time consumption. Thus, much better algorithms need to be proposed to obtain the effective channel order, bringing to sufficiently good blind approximation of measured real-world microwave radio channels. Furthermore, effective channel order determination is an important issue in the convolutive blind source separation.
CONFLICT OF INTEREST
No Conflict of Interest.
AUTHORS' CONTRIBUTIONS
Conceptualization, S.Y. Data curation, H.S. Funding acquisition, P.L. Methodology, S.Y. Project administration, J.C. Software, P.L. and S.H. Supervision, H.S. Validation, P.L., S.H. and H.S. Writing, original draft, S.Y. Writing, review and editing, S.Y. and P.L.
Funding Statement
This research was funded in part by the National Natural Science Foundation of China under Grants 61773127, 61773128 and 61727810, the Science and Technology Program of Shaoguan City of China under Grant No. SK201644, the Natural Science Foundation of Guangdong Province of China under Grant 2016KQNCX156 and 2018A030307063, and Nature Science Foundation of Hebei Province under Grant E2016106018.
REFERENCES
Cite this article
TY - JOUR AU - Senquan Yang AU - Haifeng Su AU - Pu Li AU - Songxi Hu AU - Jinru Chen PY - 2019 DA - 2019/09/12 TI - Effective Channel Order Determination Algorithm for Convolutive Blind Channel Identification JO - International Journal of Computational Intelligence Systems SP - 947 EP - 954 VL - 12 IS - 2 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.190819.001 DO - 10.2991/ijcis.d.190819.001 ID - Yang2019 ER -
