International Journal of Computational Intelligence Systems

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 12, Issue 2, 2019, Pages 513 - 518

An Improved NSGA-II Algorithm Based on Crowding Distance Elimination Strategy

Authors
Junhui Liu1, 2, *, Xindu Chen1
1Mechanical and Electrical Engineering Institute, Guangdong University of Technology, No. 100, West Outer Ring Road, Guangzhou University Town, Panyu District, Guangzhou, 510006, China
2Mechanical and Electrical Engineering Institute, Heyuan Polytechnic, University Town of East Ring Road, Yuancheng District, Heyuan, 517000, China
*Corresponding author. Email: 348060604@qq.com
Corresponding Author
Junhui Liu
Received 18 January 2019, Accepted 28 March 2019, Available Online 12 April 2019.
DOI
10.2991/ijcis.d.190328.001How to use a DOI?
Keywords
NSGA-II; Crowding distance elimination; Diversity; Convergence
Abstract

Aiming at the diversity of Nondominated Sorting Genetic Algorithm II (NSGA-II) in screening out nondominated solutions, a crowding distance elimination (CDE) method is proposed. Firstly, the crowding distance is calculated in the same level of nondominated solutions, and the solution of minimum crowding distance is eliminated; secondly, the crowding distance of residual solutions is recalculated, and the solution of minimum crowding distance is also eliminated. Repeat the above process, and stop the cycle when the nondominated solutions reaches the set number. In order to verify the effectiveness of the algorithm, experiments are carried out with the representative test functions: ZDT1, ZDT2, and ZDT3. The comparative experiments of NSGA-II, σ-Multi-objective particle swarm optimization algorithm (MOPSO), Non dominated sorting particle swarm optimization algorithm (NSPSO), and CDE were carried out respectively. By analyzing the diversity and convergence of the four algorithms, the strategy of nondominant solutions selection based on CDE has better performance.

Copyright
© 2019 The Authors. Published by Atlantis Press SARL.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

1. INTRODUCTION

In recent years, the multi-objective optimization (MOP) problem has been widely concerned and studied by many researchers from the fields of scientific research and engineering. In general, the methods to solve MOP problems can be divided into two categories: The first is objective normalization method. According to this method, a certain strategy is used to confirm the trade-off mode among multiple objectives. As a result, the MOP problem is converted into single-objective optimization problem. Finally, the solution set constituted by the optimal solutions of these single-objective is used to approximate Pareto optimal solution. Such method includes weighting method, constraint method, and goal planning method, and so on. To use objective normalization method, people shall obtain the relevant information of the objectives in advance and establish relationships among these objectives. Therefore, the method has limitations to solve many engineering problems. The second category is the multi-objective evolutionary algorithm (MOEA). During the process of MOEA, it is unnecessary to get the detailed information of various objectives in advance. Instead, the powerful global search capability of MOEA can help researchers search out the potential Pareto optimal solution. Unlike the single-objective optimization problem, the MOP aims to solve two problems: Fortify the approximation to the ideal Pareto optimal front; diversify the searched Pareto solutions [1]. As for the MOP algorithm, Nondominated Sorting Genetic Algorithm II (NSGA-II) is regarded as an important milestone [2]. It has become the benchmark for the performance comparison of other MOP algorithms [3]. NSGA-II is designed on the basis of NSGA, and it adopts the nondominated sorting and elitism strategy. The neighborhood density of individuals is calculated in accordance with the crowding distance (C.D.). The selection operators of fitness and diversity are used to improve the performance of the algorithm. The non-dominated sorting and C.D. sorting strategies of NSGA-II have been widely used in other MOP algorithms, such as the particle swarm optimization algorithm [4–6], and so on.

The improved scheme of NSGA-II mainly focuses on the following two aspects: Firstly, fortify the diversity of Pareto solution set; secondly, improve the convergence rate. The improved method of NSGA-II based on niche technology has been proposed in Literature [7]. The improved method of NSGA-II based on minimum spanning tree was put forward in Literature [8]. The improved algorithm proposed in Literature [9] has taken Pareto sorting hierarchy and congestion degree of individuals into account. According to Literature [10], when NSGA-II is used to solve the grid task scheduling problem, a genetic operator based on multiple QOS constraints has been proposed. As described in Literature [11], the researcher has taken various factors (such as time and load) into account and put forward a fuzzy genetic operator. Literature [12] has put emphasis on analyzing the causes and impacts of overlapping individuals produced during the evolutionary process of NSGA-II algorithm. Besides, the advantages to use the overlapping individual elimination method have been fully reflected via experiments. The genetic operator combined with a messy algorithm has been proposed in Literature [13]. The genetic operator is proved to improve the population diversity of NSGA-II. According to the improved method in Literature [14], the objectives shall be subject to the normalization processing. Secondly, the reference values of dynamic objectives are introduced to sort out the population. However, the improved calculation method of C.D. is barely stable, which is a fatal weakness. In addition, overmuch time shall be invested. As a result, the diversity of nondominated solution set has poor robustness. The mechanism of NSGA-II is analyzed carefully in this paper. The nondominated solutions shall be sorted by calculating the C.D. of the nondominated solutions, so as to screen out the sparse solutions and eliminate the dense solutions. The C.D. sorting of NSGA-II aims to improve the diversity of solutions. However, the impact of an eliminated solution on the C.D. of neighborhood solution has not been considered properly. In fact, for the originally dense solution, when the denser solutions around it are eliminated, it will become sparse. It is beneficial to fortify the diversity of solutions to keep such solutions. In view of this, this paper proposes an improved NSGA-II algorithm based on the C.D. elimination strategy (CDE-NSGA-II).

2. CDE ALGORITHM

According to the nondominated sorting strategy of NSGA-II, the principle is shown in Figure 1. Suppose that the population size is N, and Population Rt (the population size is 2N) is combined by the current dominated solution set Pt and the current offspring Qt. According to the dominance relation, Rt gets a series of nondominated Pareto solution set, with the order of F1, F2, …. F1 is in the top level. If the quantity of F1 is less than N, all members of F1 will be selected into Population Pt + 1. The remaining members in Population Pt + 1 will be selected from F2, F3, … until the quantity of member reaches N. The order of the first member in F3 is less than N, while the order of the last member is greater than N. In order to keep the diversity of the population, NSGA-II algorithm is used to perform C.D. sorting to F3, and the individuals with large C.D. are given priority to entering Population Pt + 1.

Figure 1

Nondominated sorting strategy of Nondominated Sorting Genetic Algorithm II (NSGA-II).

2.1. Problems in C.D. Sorting of NSGA-II

After completing nondominated sorting, the C.D. of each solution within the nondominated solution set at the same level is calculated based on the objective space [2]. The C.D. of the extreme solution (the maximum or minimum solution of all objectives within the objective space) shall be set as infinity all the time (it shall be set as a big real number in the practical operation, such as 1.0e + 50), while other solutions shall be sorted out for all objectives. The C.D. of other solutions shall be defined as the average value of target distances between two adjacent solutions. Among 10 nondominated solutions as shown in Figure 2, five solutions has been selected in accordance with the C.D. According to the C.D. sorting algorithm of NSGA-II, the C.D. for all solutions are listed in Table 1. In which: The C.D. of Solutions 1–2 and 8–10 are so large that all of them shall be kept, while the C.D. of Solutions 3–7 is too small to be saved. As shown in Figure 3, after the selection, the results of Solutions 2 and 8 are not reasonable due to the sparse distance between them.

No. 1 2 3 4 5
C.D. 1.0e + 50 0.71 0.29 0.35 0.41
No. 6 7 8 9 10
C.D. 0.33 0.26 0.37 0.51 1.0e + 50

C.D., crowding distance.

Table 1

Crowding distance of nondominated solutions.

Figure 2

Ten nondominated solutions.

Figure 3

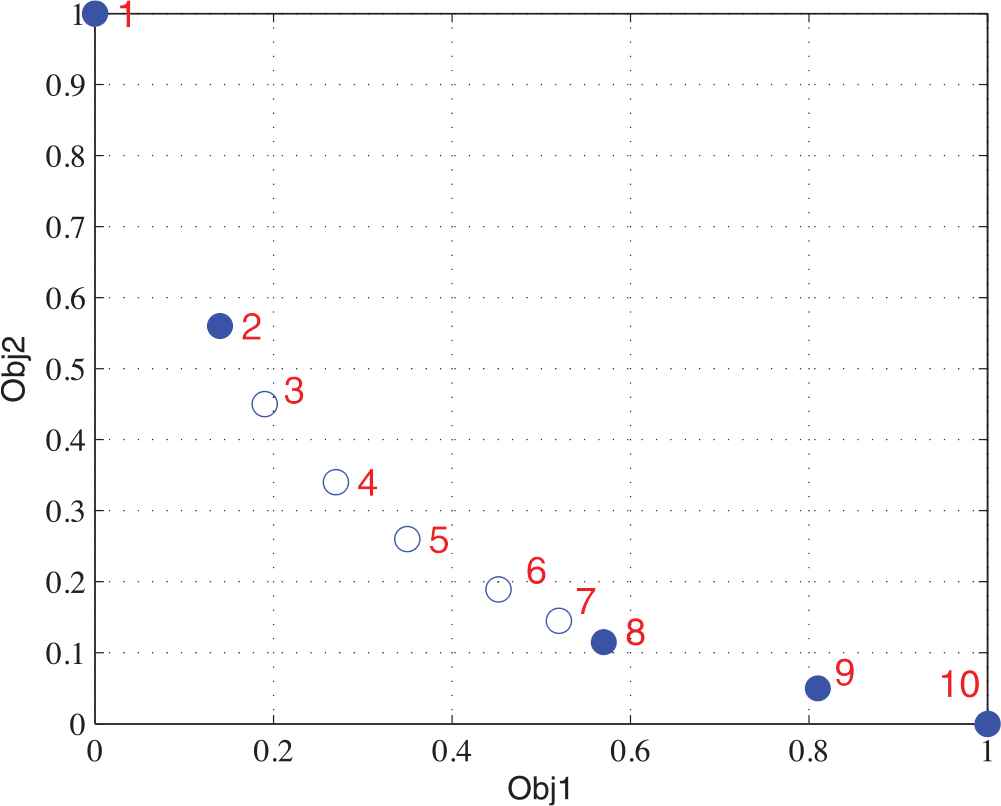
Screening results with Nondominated Sorting Genetic Algorithm II (NSGA- II).

2.2. CDE Algorithm

The NSGA-II algorithm is generally used for MOP problems. Unconstrained MOP problems can be defined as follows:

Min  Fx=f1x,f2x,⋯,fnx
s.t.x= x1,x2,⋯,xk∈Xu= u1,u2,⋯,uk and l=l1,l2,⋯,lk,
where F(x) is the objective function vector, x is a decision parameter vector, X is the decision parameter space, u and l are the upper and lower bounds of the decision parameter, respectively.

C.D. reflects the density of the surrounding individuals of a given individual in a population. It can be expressed as the sum of the largest rectangle and width by the surrounding individuals. The C.D. nd is defined as

nd=nd+fmi+1−fmi−1fmmax−fmmin,
where, fmmax  and fmmin are the maximum and minimum of objective function fm, m is the individual of solution set. nd is initially set to 0.

For the choice of nondominant solutions, the following methods are adopted:

i≺j,   ifirank< jrankirank= jrank and ndi>ndj.

When the rankings of two nondominant solutions are different, the solutions with smaller rankings will be selected. When two solutions belong to the same Pareto frontier, the solution with large C.D. will be chosen.

In order to overcome the shortcoming of the C.D. sorting algorithm in NSGA-II, the CDE algorithm has been proposed in this paper. The basic idea of CDE algorithm is as follows: The problem shown in Figure 2 is to calculate the C.D.. Since the C.D. of Solution 7 is smallest, Solution 7 has been deleted directly (solution labeled a in Figure 4); the C.D. of the remaining solutions is recalculated. Considering that the C.D. of Solution 3 is minimum, Solution 3 is deleted as well (solution labeled b in Figure 4). In the same way, only five solutions are left behind as shown removal order from c to e in Figure 4. According to the results shown in Figures 3 and 4, the solutions screened out with CDE algorithm are more uniform and diverse than those solutions screened out with the NSGA-II algorithm.

Figure 4

Screening results with crowding distance elimination (CDE) method.

2.3. The Flow and Time Complexity of CDE Algorithm

The task of CDE algorithm is to screen and keep n solutions from the nondominated solution F (m solutions in total) in accordance with the C.D. The pseudocode of CDE algorithm flow is as follows:

Crowding_Distance_Elimination (F, m, n) {

While m! = n

for i = 1 : m

F[i].distance = 0; // Initialization

end

for j = 1 : J // Objective from 1 to J

F= sort (F, j); // Sort by objective j

interval = F[m].value − F[1].value;

// Max - min of objective j

if interval == 0

interval = 1.0e − 20;

//Prevent all individuals of objective j from overlapping

end

F[m].distance = 1.0e + 50;

// Maximum crowding distance

F[1].distance = 1.0e + 50;

// Maximum crowding distance

For k = 2 : m − 1

F[k].distance = (F[k + 1].value - F[k − 1].value) / interval;

end

end

i = Min_Distance (F);

// Find the solution of minimum crowding distance

F[i] = [];

// Delete the solution of minimum crowding distance

m = m − 1; // Enter the next cycle

end}

The worst case in C.D. sorting algorithm is to select N solutions from 2N (N refers to the population size). The time complexity for single C.D. sorting algorithm is OJ2N log2N (J refers to the number of objectives). During the sorting process, the time complexity for the first sorting in CDE algorithm is OJ2N log2N, and the time complexity for the second sorting is OJ2N−1 log2N−1, and the time complexity for the last sorting is OJN logN. Therefore, the overall time complexity ε is as follows:

ε=O∑i=N2NJi logi.

3. EXPERIMENT AND DISCUSSION

3.1. CDE Algorithm

Three test functions are selected to verify the algorithm in this paper. The three test functions are the ZDT series functions. The ideal Pareto solutions of ZDT1, ZDT2, ZDT3 are convex, concave, and discontinuous, respectively. These test functions are quite representative.

ZDT1:

min f1x1=x1min f2x=g1−f1/ggx=1+9∑i=2mxim−1s.t. 0<xi<1, i=1,2,…,30

ZDT2:

min f1x1=x1min f2x=g1−f1/g2gx=1+9∑i=2mxim−1s.t. 0<xi<1,  i=1,2,…,30

ZDT3:

min f1x1=x1min f2x=g1−f1/g−f1/gsin10πf1gx=1+9∑i=2mxim−1s.t. 0<xi<1,  i=1,2,…,30

There are two goals for MOP: 1) Converge to the ideal Pareto front; 2) Maintain the diversity of Pareto solutions. The convergence degree and diversity are used to evaluate the performance of these two goals. The convergence degree is used to measure the distance between Pareto solutions P obtained by algorithm and the ideal Pareto solutions P*. First of all, 500 solutions distributed in the ideal Pareto front uniformly shall be selected to constitute P*; secondly, calculate the Euclidean distance between each solution in Pareto solution set P and the most proximate solution in P*. The average value of the distances shall be regarded as the convergence degree. The diversity Δ is defined as follows:

Δ=df+dl+∑i=1N−1|di−d|df+dl+N−1d,
where di is the distance between adjacent solutions in P; d is the average value of all di; df and dl are the Euclidean distances between the boundary solution of P and the extreme solution in P*.

3.2. Comparative Analysis of Algorithms

The comparison test has been carried out by using NSGA-II, σ-MOPSO [15], NSPSO [16], and CDE-NSGA-II developed in this paper. The parent population size, crossover probability, mutation probability, and number of iteration are set as 50, 0.9, 0.2, and 500, respectively. Therefore, there are 25,000 times of function evaluations. In order to reflect the repeatability properly, each group of experiments has been implemented 100 times. The mean and variance of convergence degree and diversity are calculated as well. The data of NSGA-II has been introduced from the literature [2], and the data of NSPSO and σ-MOPSO derive from literature [17]. According to the definition, the smaller value of mean and variance, the better the algorithm is. The test data are shown in Tables 2 and 3.

Algorithm Index ZDT1 ZDT2 ZDT3
NSGA- II M 0.0335 0.0724 0.115
VAR 0.0048 0.0317 0.0079
σ-MOPSO M 0.0164 0.0058 0.102
VAR 0.0005 0.021 0.0024
NSPSO M 0.0013 0.0009 0.0042
VAR 0.0003 0.011 0.0021
CDE-NSGA-II M 0.0006 0.0003 0.0033
VAR 0.0002 0.006 0.0016

NSGA-II, Nondominated Sorting Genetic Algorithm II; CDE, crowding distance elimination.

Table 2

The mean and variance of convergence degree.

Algorithm Index ZDT1 ZDT2 ZDT3
NSGA- II M 0.39 0.431 0.739
VAR 0.0019 0.0047 0.0197
σ-MOPSO M 0.399 0.39 0.76
VAR 0.0073 0.0046 0.0035
NSPSO M 0.681 0.639 0.832
VAR 0.0134 0.0011 0.0089
CDE-NSGA-II M 0.241 0.401 0.57
VAR 0.0002 0.0016 0.0014

NSGA-II, Nondominated Sorting Genetic Algorithm II; CDE, crowding distance elimination.

Table 3

The mean and variance of diversity.

The experimental results of several MOP algorithms are shown in Figure 5(a–d). Compared with other algorithms, CDE-NSGA-II has the fastest convergence rate; as for diversity, the proposed algorithm also has the best performance.

Figure 5

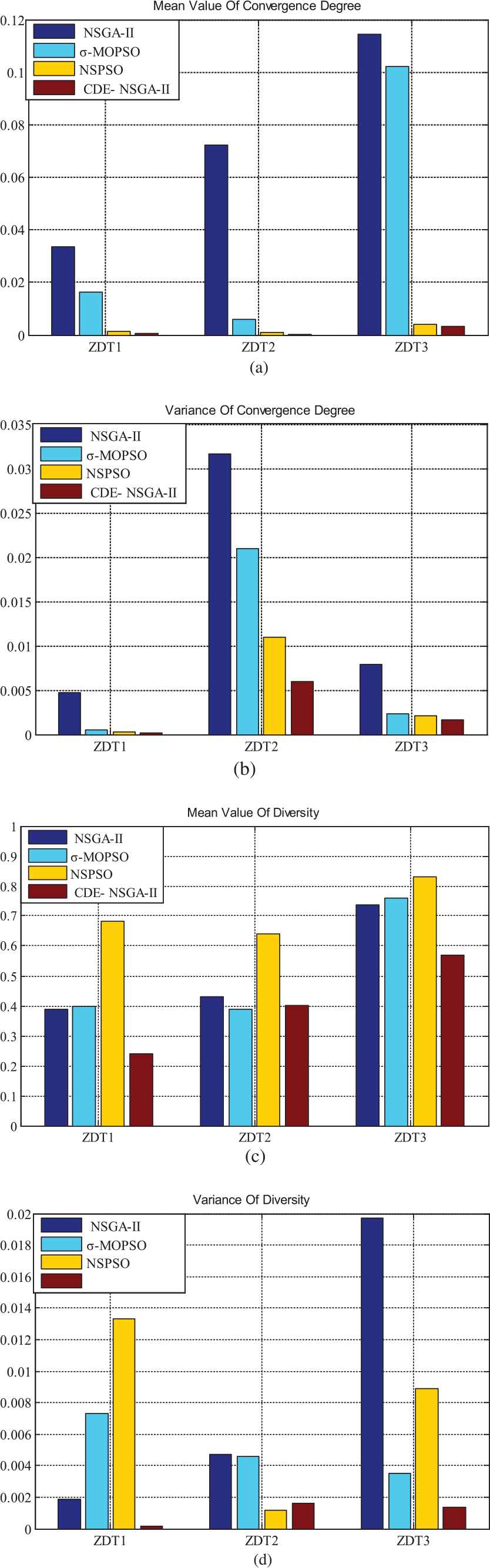
Value of mean and variance for convergence degree (a), (b) and diversity (c), (d).

To reflect the convergence degree and diversity intuitively, the experiment has been performed again by using NSGA-II and CDE-NSGA-II. In this case, the numbers of iteration are set as 500 and 1000. According to the output results shown in Figure 6(a–c), the proposed algorithm is superior to NSGA-II in terms of the convergence rate. Besides, the distribution of Pareto solutions is more even. As for solutions obtained by NSGA-II algorithm, the solutions at circular marker are too dense, and around it are too sparse.

Figure 6

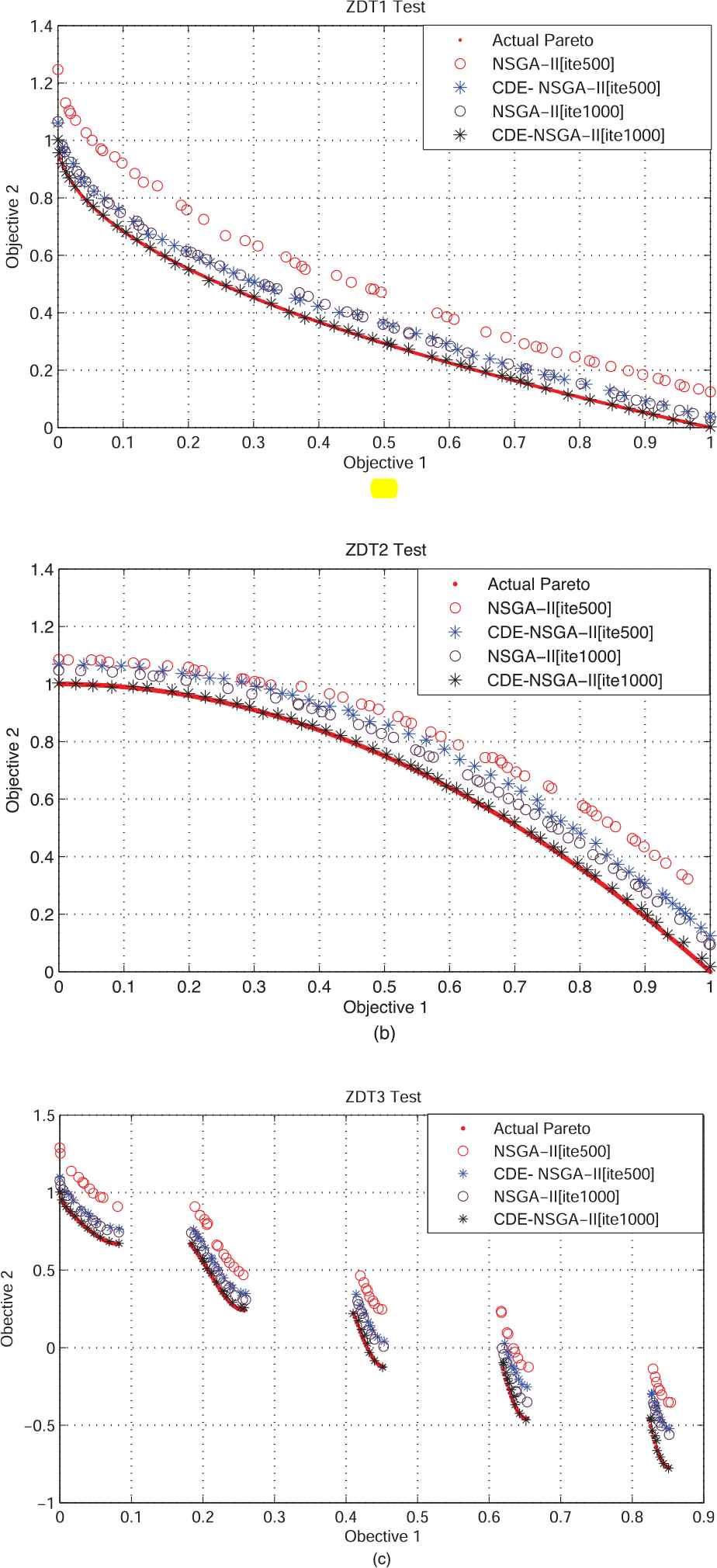
Pareto solutions obtained from Nondominated Sorting Genetic Algorithm II (NSGA- II) and crowding distance elimination NSGA-II (CDE-NSGA-II) in ZDT1 (a), ZDT2 (b), and ZDT3 (c).

Compared with NSGA-II, CDM-NSGA-II is provided with an improved C.D. sorting strategy but offers no change to the selection, crossover, and mutation. With the application of the ZDT1 ∼ ZDT3 functions, CDM-NSGA- II has experienced a sound improvement in terms of its convergence and diversity, which verifies the effectiveness of CDE algorithm.

4. CONCLUSION

By virtue of in-depth discussion and analysis on the mechanism of NSGA-II C.D. sorting, a new method is proposed to overcome the defects: a strategy based on CDE method. According to the experimental results, CDM-NSGA-II is superior to NSGA-II, σ-MOPSO, and NSPSO in terms of convergence and diversity. Therefore, CDM-NSGA-II is highly competitive.

However, the proposed method will increase the computational complexity. When the number of objective functions reaches a certain order of magnitude, the number of variables that need to be involved is also very large, which will lead to a sharp increase in the amount of computation and affect the speed of optimization calculation. Therefore, our future work will optimize the computational complexity of the algorithm and reduce the running cost of the algorithm on the premise of ensuring the convergence and diversity of the solution set.

ACKNOWLEDGMENTS

This research is supported by Science and Technology Planning Project of Guangdong Province under Grant nos. 2015B090921007 and 2015B010919001.

REFERENCES

1.M. Qinliang and H. Changhua, Survey of multi-objective evolutionary algorithm and its applications in the field of automatic control, Control Decis, Vol. 21, No. 5, 2006, pp. 481-486.
2.K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, A fast and elitist multiobjective genetic algorithm: NSGA-II, IEEE Trans. Evol. Comput., Vol. 6, 2002, pp. 182-197.
3.C.A. Coello Coello, Evolutionry multi-objective optimization: a historical view of the field, IEEE Comput. Intell. Mag., Vol. 1, No. 1, 2006, pp. 28-36.
4.A. Duggirala, R.K. Jana, R.V. Shesu, and P. Bhattacharjee, Design optimization of deep groove ball bearings using crowding distance particle swarm optimization, Sādhanā, Vol. 43, No. 1, 2018, pp. 9.
5.K.-H. Chen, L.-F. Chen, and C.-T. Su, A new particle swarm feature selection method for classification, J. Intell. Info. Syst., Vol. 42, No. 3, 2014, pp. 507-530.
6.A. Ebrahim Sorkhabi, M. Deljavan Amiri, and A.R. Khanteymoori, Duality evolution: an efficient approach to constraint handling in multi-objective particle swarm optimization, Soft Comput., Vol. 21, No. 24, 2017, pp. 7251-7267.
7.X.Q. Chen, Z.X. Hou, L.M. Guo, and W.C. Luo, Improved multi-objective genetic algorithm based on NSGA-II, J. Comput. Appl., Vol. 26, No. 10, 2006, pp. 2453-2456.
8.L.I. Mi-Qing, Improved NSGA-2 algorithm based on minimum spanning tree, Comput. Eng. Appl., 2007, pp. 170-179.
9.L. Xuhong, L. Yushu, and Z. Guoyin, Improvement of multi-objective optimization algorithm NSGA-II, Comput. Eng. Appl., Vol. 41, No. 15, 2015, pp. 73-75. 1002-8331-(2005)15-0073-03
10.H. Songfa and Z. Ying, NSGA-II based grid task scheduling with multi-QoS constraint, in Third International Conference on Genetic and Evolutionary Computing (Guilin), 2009.
11.R. Salimi, H. Motameni, and H. Omranpour, Task scheduling with Load balancing for computational grid using NSGA II with fuzzy mutation, in IEEE International Conference on Parallel Distributed and Grid Computing (Solan), 2013, pp. 79-84.
12.X. Jiongliang and Z. Jinhua, Reaserch on cause for overlapping solutions and on their influence in NSGA-II, Comput. Eng. Appl., Vol. 44, No. 29, 2008, pp. 69-72.
13.D. Guo, J. Wang, J. Huang, R. Han, and M. Song, Chaotic-NSGA-II: an effective algorithm to solve multi-objective optimization problems, in International Conference on Intelligent Computing and Integrated Systems (Guilin), 2010, pp. 20-23.
14.R. Patel, M.M. Raghuwanshi, and L.G. Malik, An improved ranking scheme for selection of parents in multi-bbjective genetic algorithm, in International Conference on Communication Systems and Network Technologies (Jammu), 2011, pp. 734-739.
15.S. Mostaghim and J. Teich, Strategies for finding good local guides in Multi-objective Particle Swarm Optimization (MOPSO), in Proceedings of the 2003 IEEE Swarm Intelligence Symposium (Indiana), 2003.
16.L. Xiaodong, NSPSO: a non dominated sorting particle swarm optimizer for multiobjective optimization, in Genetic and Evolutionary Computation GECCO (Berlin, Heidelberg), 2003.
17.P.K. Tripathi, S. Bandyopadhyay, and S.K. Pal, Adaptive multi-objective particle swarm optimization algorithm, in the Proceeding of IEEE Congress on Evolutionary Computation (Singapore), 2007.
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
International Journal of Computational Intelligence Systems
Volume-Issue
12 - 2
Pages
513 - 518
Publication Date
2019/04/12
ISSN (Online)
1875-6883
ISSN (Print)
1875-6891
DOI
10.2991/ijcis.d.190328.001How to use a DOI?
Copyright
© 2019 The Authors. Published by Atlantis Press SARL.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Junhui Liu
AU  - Xindu Chen
PY  - 2019
DA  - 2019/04/12
TI  - An Improved NSGA-II Algorithm Based on Crowding Distance Elimination Strategy
JO  - International Journal of Computational Intelligence Systems
SP  - 513
EP  - 518
VL  - 12
IS  - 2
SN  - 1875-6883
UR  - https://doi.org/10.2991/ijcis.d.190328.001
DO  - 10.2991/ijcis.d.190328.001
ID  - Liu2019
ER  -