Wave reflection: Myth or reality?
- DOI
- 10.1016/j.artres.2012.01.005How to use a DOI?
- Copyright
- © 2012 Association for Research into Arterial Structure and Physiology. Published by Elsevier B.V. All rights reserved.
- Open Access
- This is an open access article distributed under the CC BY-NC license.
Introduction
The precise role and importance of arterial wave reflections, their impact and implications have been for a long time – and continue to be – a subject of heated debate. In our opinion, much of the substance of this debate arises from an assessment of arterial hemodynamics using concepts or paradigms that do not fully match the complexity of the physics of wave travel and reflection in the arterial system. In what follows, we elaborate on two of these concepts: the arterial tree as a single tube, and the arterial tree as a reservoir-wave system in an attempt to separate facts from fiction.
What is clear and undisputed in arterial hemodynamics is the fact that with each contraction, the heart generates a forward running pressure and flow wave which travels down the arterial tree with a finite wave speed. It is only if the heart were ejecting in a uniform (with constant characteristic impedance) infinitely long tube that this incident wave would not lead to any reflection. Given that the arterial tree is a complex network with continuous changes in diameter (tapering vessels) and elastic properties and bifurcations, it is as certain as the sunrise in the morning that these give rise to reflections, which affect both the pressure and the flow waves traveling in the arterial tree. As such, there is very little myth in arterial wave reflection. It is a given fact.
The measured arterial pressure and flow waves are thus composites, composed of waves traveling in the “forward” (from the heart to the periphery) and the “backward” direction (from the periphery toward the heart), which we refer to as reflected waves. These wave effects are easily evidenced when measuring pressure pulses along an arterial path, e.g. along the aorta,1,2 which will demonstrate a clear time delay and a continuous change in the morphology of the wave with, generally, steepening of the wave front and an increase in the amplitude of the wave from proximal to distal sites. These effects are also observed along the aortic-brachial pathway, leading to a discrepancy between central and peripheral blood pressure.
Though wave travel and reflection can obviously be studied in vivo, they can also be mimicked in detail using computer models of the arterial tree, with most work done using 1-dimensional arterial network models which incorporate the topology of the arterial tree (see e.g.3–8). These models provide highly realistic output in terms of pressure and flow waves, and have been validated against human data.5 The difficulty of these models, however, is the very large number of parameters that one needs to set up the model. This also hampers their practical use, as it is virtually impossible to tune these models to study individual patients (i.e., provide a model parameter set specific for an individual).
To reduce the complexity of the problem at hand, and provide practical and comprehensible tools for the analysis and interpretation of hemodynamic signals (pressures and flows) and the functional assessment of the arterial tree, simplified models and concepts or “paradigms” are in use, such as for instance the notion of the arterial tree as single tube with a discrete reflection at a given “effective” length (Leff).9 While the use of these simplified concepts can be perfectly legitimate and appropriate for a given purpose, the problem is that too often the assumptions and reductions behind these conceptual models are forgotten or simply ignored. Coupled to the inadequate comprehension of the complex reality of wave travel and reflection in the arterial system, this contributes to the general use of these simplified concepts outside the scope for which they are valid, which carries the danger that they become the frame of reference within which hypotheses are formulated and verified.
The arterial system’s fingerprint: input impedance
An elegant tool to assess these conceptual models of the arterial system is the analysis of how well the so-called input impedance (Zin) of the arterial tree is matched by the model’s input impedance. Zin fully describes the relation between pressure and flow at the entrance of the (model of the) arterial tree.10,11 It is assessed in the frequency domain, meaning that it is obtained after decomposing the (ascending) aortic pressure and flow into a series of sinusoidal harmonics using the Fourier theorem. As such, instead of considering the pressure and flow signals as a whole, they are seen as the superposition of a steady component and a series of sinusoidal harmonics. One can then study the system at a given frequency, with (i) the input impedance modulus providing the ratio of the amplitude of the pressure and flow harmonics, and (ii) the input impedance phase angle indicating the time delay between the pressure and the flow. A negative phase angle indicates that the flow harmonic reaches its maximum before the pressure does (flow leads pressure); a positive phase angle indicates the opposite (flow lags behind pressure). A phase angle of zero indicates that there is no time delay between pressure and flow. As illustrated in Fig. 1, a typical in vivo input impedance pattern is characterized by:
- -
a high modulus at 0 Hz (which is the ratio of mean pressure and mean flow, and hence is the total vascular resistance) and zero phase angle;
- -
a fast drop in modulus and a negative phase angle in the low frequency range (first 3 harmonics);
- -
a tendency toward a plateau value for the impedance modulus and a zero phase angle for the higher harmonics.
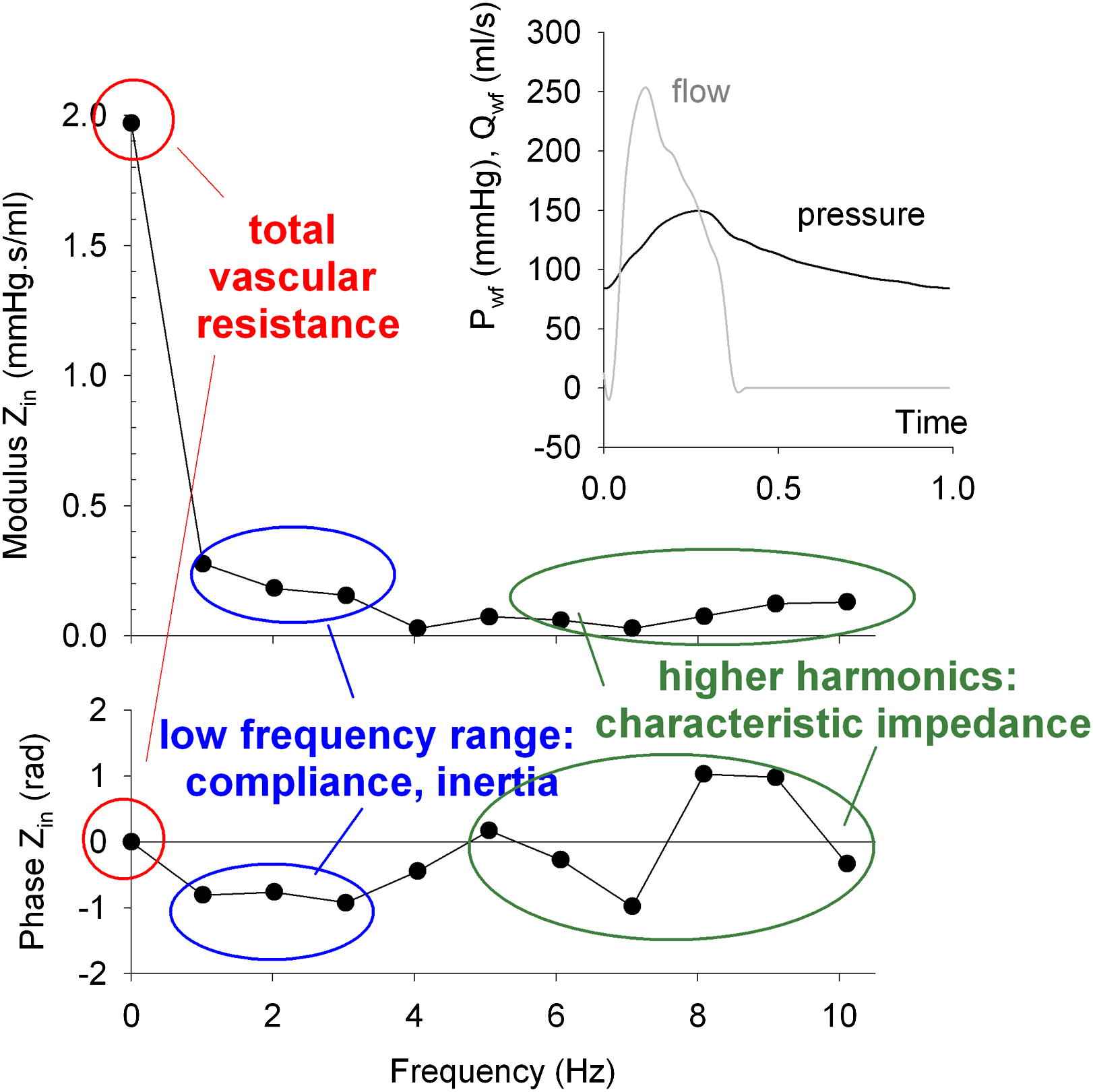
Input impedance modulus (top left) and phase (bottom left) derived from the measured pressure and flow signals displayed in the upper right panel.
Any model that is capable of mimicking the specific features of this input impedance spectrum is thus able to mimic the behavior of the arterial tree, at least from the perspective of the heart. This is the case for the above mentioned complex arterial tree models, but much more simple models are also capable of doing this, including the single tube model and even models which do not explicitly include any wave travel effects at all, the so-called lumped parameter models.
The arterial system is not a single tube
The widespread notion that central aortic pressure can be considered as the superposition of a forward wave (generated by the heart) which travels down the aorta, reflects at a certain distance (Leff) with the generation of a backward component which adds to the forward wave, has at least two sources.
First, when given the appropriate parameters (radius, wall thickness, stiffness, tube length, reflection coefficient at the end), a single tube model will generate an input impedance spectrum which displays some features of a measured spectrum, in particular the appearance of a discrete minimum in the input impedance modulus9,12 due to destructive interference for the pressure wave at the frequency where the wavelength is exactly 4 times the length of the tube. This pattern resembles the pattern of measured input impedance spectra, as illustrated in Fig. 2 for a tube with the specifications listed in the Figure.
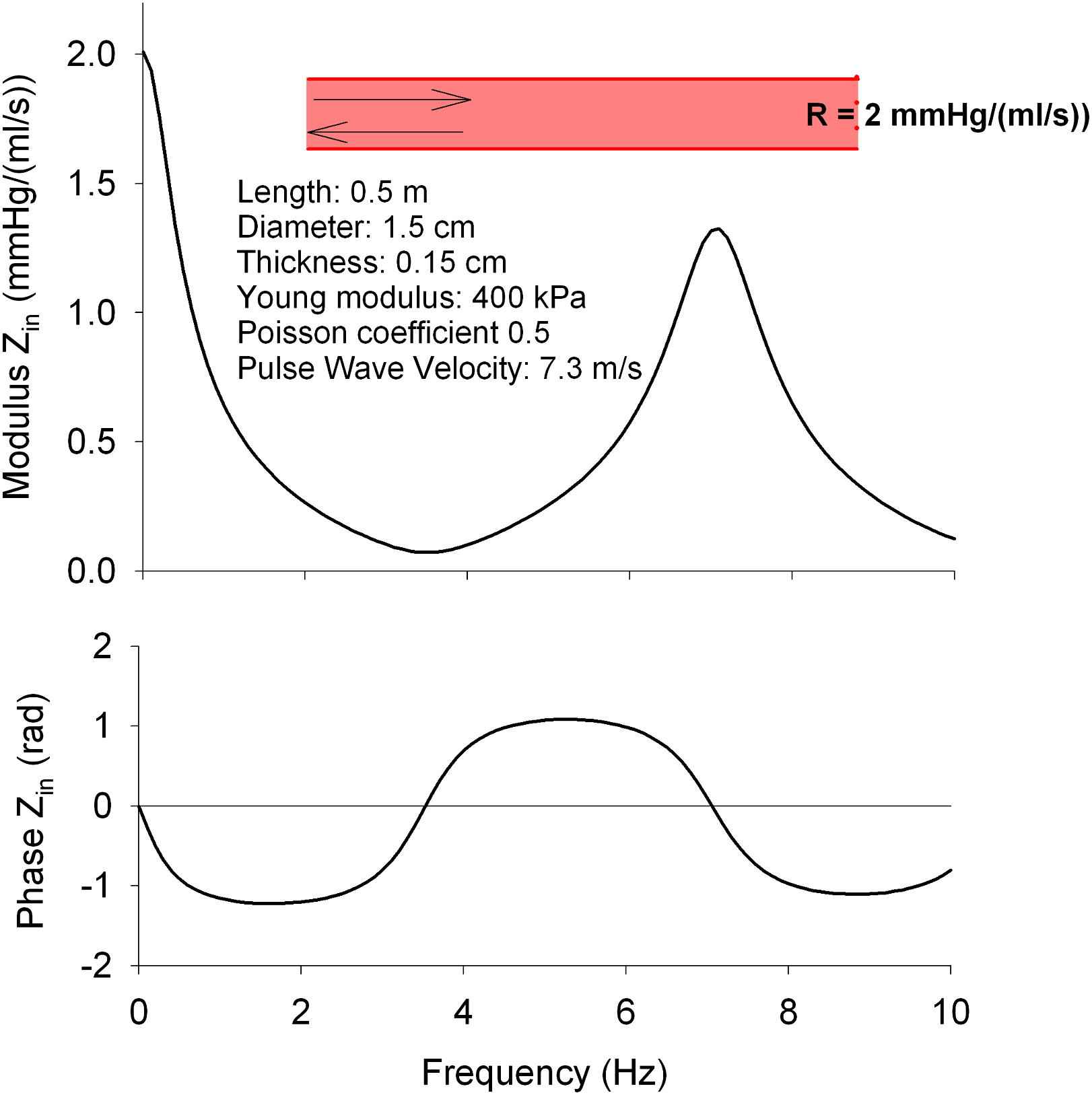
Input impedance of a single linear elastic tube model with a length of 50 cm, terminated by a simple resistance. See figure for the model parameter specifications. The modulus displays a distinct minimum at about 3.6 Hz. For this frequency, the wavelength is 2 m, i.e. 4 times the length of the tube.
Second, it has been shown by Westerhof et al. that, when the characteristic impedance (the ratio of pressure and flow in the absence of wave reflections; Zc) is known at a particular place (e.g. at the entrance of the aorta), it is possible to decompose the pressure (and flow) wave into a forward (Pf) and backward (Pb) component13:
When using the single tube model as the reference frame, Pb is directly linked to Pf, and is simply its reflected component. As such, when analyzing pressure waves along the aorta and assuming the reflection site to be located somewhere in the distal aorta, one would expect to find a logical sequence with Pf traveling from the root to the distal aorta, and Pb traveling from the distal aorta to the root. This, however, does not happen in vivo, and there is no apparent logic in the timing of Pb.14 The principal reason for this observation is the fact that there is no such thing as a single discrete reflection site in the arterial tree. There is not necessarily a clear relationship between Pb measured at different locations, as distinct factors might have played a role in the genesis of Pb at that specific location.
Several authors have tried to pinpoint one or more discrete arterial reflection sites in the past,1,2,15,16 with the aorto-iliac bifurcation and the branching points to the renals and gastro-intestinal arteries among the “usual suspects”. An elegant study disproving the hypothesis of discrete reflection sites was done by Pythoud et al. Re-analysing data from an older animal study (where discrete reflections were generated by inflation of a balloon at different levels along the aorta17), they described a technique for constructing a reflection profile (i.e. reflection amplitude versus distance from the heart).18 Their data clearly showed that the arterial tree has a reflection profile characteristic of distributed and diffuse reflections, rather than from discrete reflections (Fig. 3). Interestingly, these animal data already indicated that in order to observe the effect of an aortic occlusion at the ascending aorta, the occlusion has to be done sufficiently proximal. A total occlusion just proximal to the aorto-iliac bifurcation hardly has an effect on ascending aorta pressure hemodynamics.17 An important factor contributing to the diffuse character of wave reflection might actually be aortic taper. We demonstrated in an analytical study in a tube model that a tapering angle of only 2° reduces the effective length of a tube of 50 cm to about 30 cm, thus shifting the “apparent” reflection site by 20 cm.19
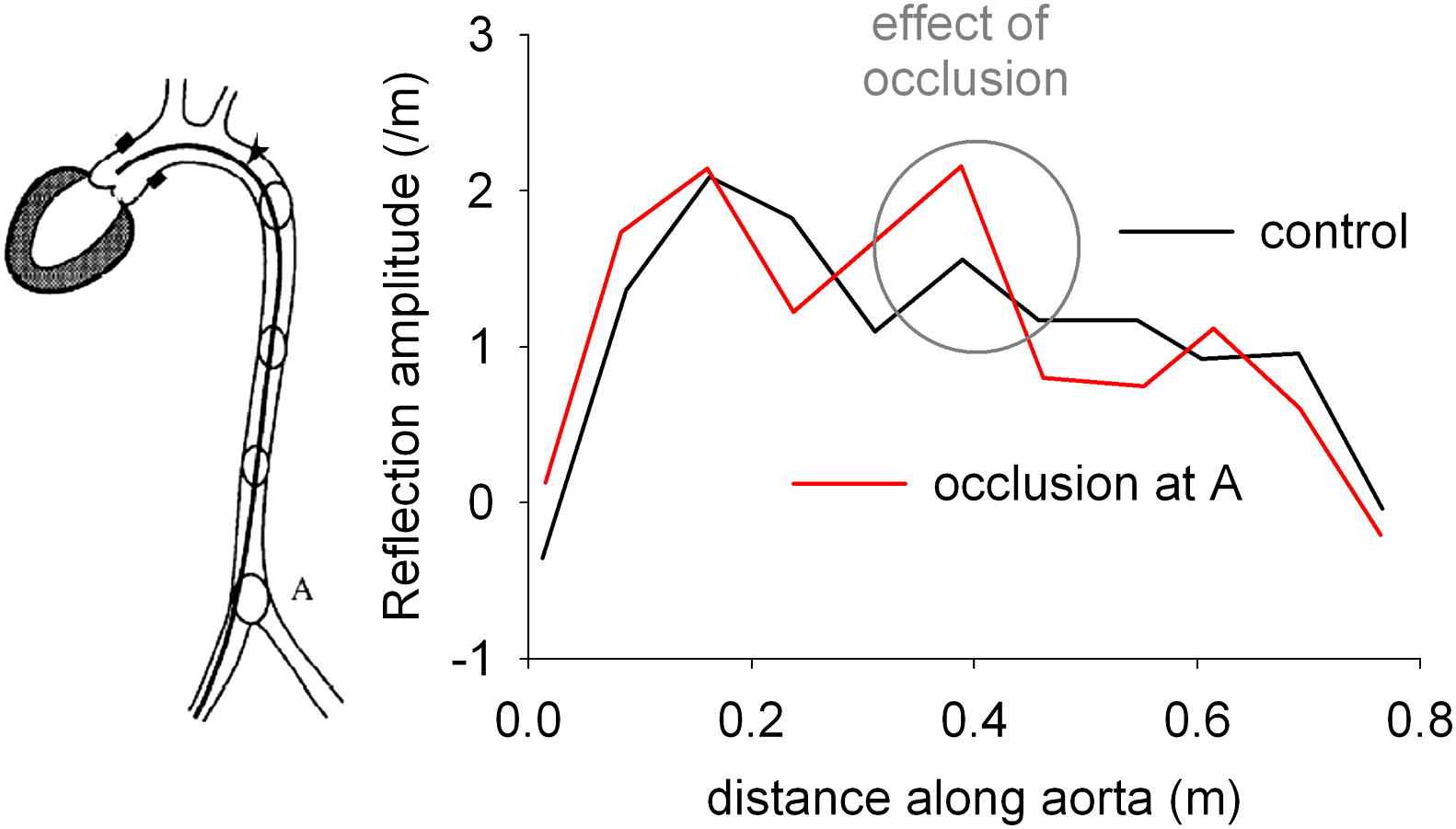
Reflection profile of the aorta of a dog indicating the strength of reflections arising from a certain distance from the aortic root. The absence of a clear peak is indicative for scattered, diffuse reflection, disproving the existence of (a limited number of) discrete reflection sites. Total occlusion at site A (red curve) generates an increase in the reflection amplitude from the reflection site, yet albeit to a relatively moderate extent. Reconstructed from.17,18 (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
The above has several implications. First, there is no direct and trivial mechanistic link between the forward and backward pressure component that one finds after decomposing the ascending aorta pressure wave at a given location. This also means that one cannot use the time delay between Pf and Pb to obtain information on the pulse wave velocity in the aorta, as it is impossible to pinpoint the origin of Pb. Devices intrinsically relying on the hypothesis of the existence of a discrete reflection site (such as the Arteriograph) are therefore doomed to be inaccurate.20 Second, the aortic occlusion experiments of Vandenbos et al.17 also demonstrated that in order for reflections to reach the ascending aorta, they must be generated relatively close to the heart. This undermines the hypothesis that peripheral beds and the transition zones from large to small arteries are an important source of reflection. On the other hand, it has been demonstrated that vasodilators such as nitroglycerin do have a profound effect on the central pressure waveform, thought to result from a decrease in wave reflection.21,22 As these vasodilators are assumed to mainly act on more peripheral, muscular arteries, it is hard to reconcile these findings, and there must be a degree of cross-talk between large and small artery function. Also, the transition from large elastic to smaller, more muscular arteries is gradual. The composition of the arterial wall even varies along the aorta, the abdominal aorta being more muscular than the proximal part, leading to higher regional pulse wave velocity.23 As such, agents acting on smooth muscle tone might also have a more proximal effect.
There appears to be no role for an arterial reservoir in wave reflection analysis
One of the most simple conceptual models, which recently regained attention with the work of Tyberg and colleagues,14,24,25 is the “windkessel” model which was first introduced by Otto Frank.26 The model captures two important features of the arterial tree: the global cushioning function of the large elastic arteries by means of the compliance, and the resistance to flow generated by the smaller arteries. This model is particularly capable to match the input impedance in the low frequency range (first 2–3 harmonics), thus capable of capturing the ”slow” phenomena in the arterial tree and predicting the gross features of the pressure waveform such as its total amplitude (the pulse pressure)27 or the exponential decay in diastole.28 Thanks to the presence of the compliance in the model, a phase shift is introduced between the pressure and flow harmonics, causing flow to reach its maximum before the pressure does (negative phase angle for these lower harmonics). The model, however, fails to describe the “fast” phenomena, and its impedance deviates from measured spectra in the higher frequency range (>3rd – 4th harmonic).
In recent works, Parker and Tyberg and colleagues introduced a hybrid conceptual model of the arterial system, where the pressure wave is considered as the superposition of a slow “reservoir component” and a fast excess pressure which is ascribed to wave travel and reflection. As such, when studying effects of wave travel, it is claimed that this analysis should be done on the excess pressure component alone, first correcting pressure waves for the reservoir component. Wang et al. applied this method in dogs and used wave intensity analysis to assess the nature and direction of waves in the aorta, obtaining results that were quite different from the conventional analysis.14 In particular, the reservoir-wave version of wave intensity displays a backward expansion (i.e. pressure decreasing) wave suggestive of open-end (i.e. negative) wave reflection, in contrast to the conventional analysis which predicts a pressure-increasing reflected wave. Overall, this concept suggests a far less important role for wave reflections in the genesis of the pressure wave, the dominating factor being the reservoir pressure.
The reservoir-excess pressure concept, however, is not generally accepted. The reason for this may lie in the fact that two distinct conceptual models (wave travel and lumped parameter model) have been mixed together to describe a single physical phenomenon, thereby leading to some conceptual difficulties. For example, the windkessel component does not incorporate any wave travel at all, which seems difficult to match with the observation that there is a clear and marked time delay when waves are measured along the aorta, while the presence of a true windkessel component would imply that the reservoir component changes simultaneously throughout the reservoir. In recent work, Mynard et al. questioned the reservoir-excess pressure concept, studying the effect of the reservoir pressure correction first in simple models with well-defined reflections (both the site and amplitude of the reflection), gradually increasing model complexity and with final application in vivo.29 They concluded that the reservoir pressure correction introduces spurious, non-existing waves when analysed in well-defined model settings. Reflected compression waves are suppressed, expansion waves are artificially introduced or get amplified (see also Fig. 4). Similar observations were also reported earlier by Borlotti and Khir in a conference proceeding.30
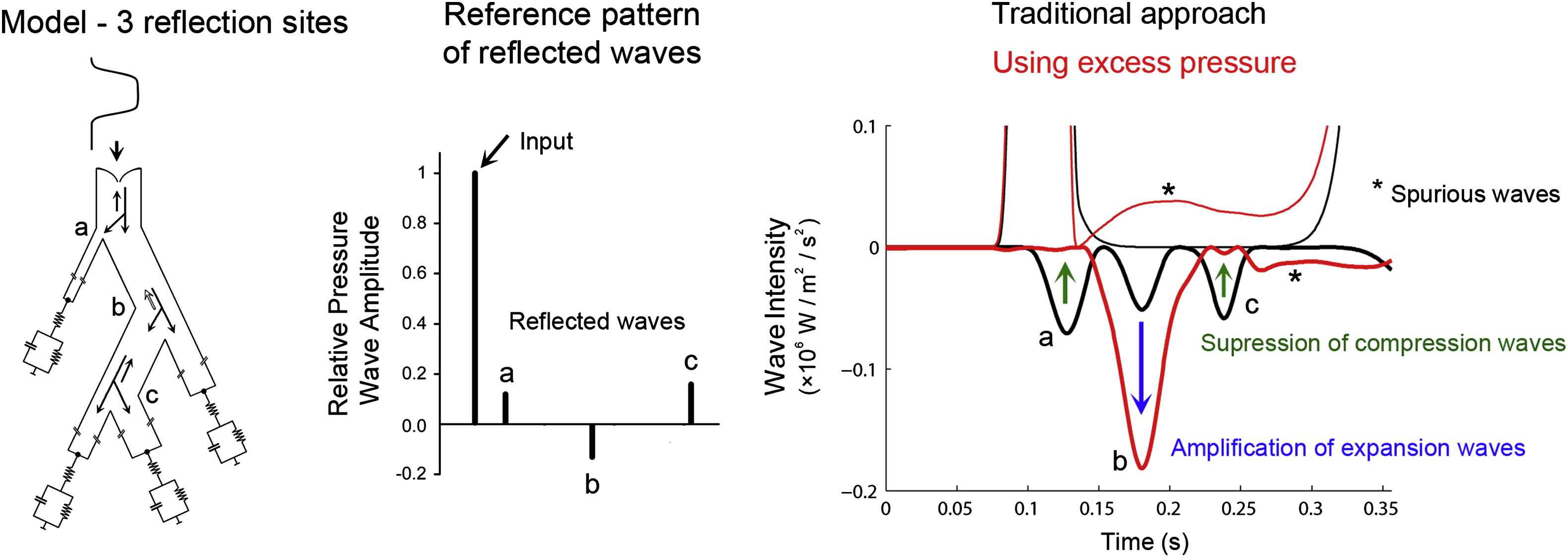
Left: arterial network model setting with 3 distinct reflection sites, giving rise to backward compression waves (a and c) and a backward expansion wave (b) (middle panel). Right: traditional wave intensity analysis reveals the expected reflections and correctly predicts the nature of these waves. In contrast, wave intensity analysis based on the excess pressure suppresses the reflected compression waves (a and c) and amplifies the backward expansion wave.
As such, although the reservoir-wave concept remains an intriguing concept, it appears that it leads to a flawed interpretation of hemodynamic data. Probably, the strict interpretation of the arterial tree as a reservoir is a too simple (mathematical) approximation of a reality which is more complex. The reservoir-like behavior is intricately linked and intertwined with the physics of wave travel and reflection in the aorta. As phrased by Mynard et al., the lumped parameter model is a reduced version of the 1-dimensional model, implying that all phenomena accounted for by the windkessel model are also explicable using the more general 1-dimensional models, including the exponentially decaying pressure in diastole.29 As such, one cannot simply differentiate between a wave and reservoir component, as the latter is just a manifestation of (complex) wave behavior. It also explains why the supposedly wave-independent reservoir component in fact behaves like a wave, propagating along the arterial tree.
Conclusion
The urge to come up with simple pulse wave analysis tools to be used in the clinical setting seems to conflict with reality: wave reflection is complex and there is at present no simple model or paradigm that sufficiently captures all required elements to provide a comprehensive yet full view of arterial wave travel and reflection. Extrapolation or over-interpretation of simple conceptual models may lead to spurious effects and possible erroneous interpretation of cardiovascular physiology. Central aortic hemodynamics are thus still not fully understood and that we continue to struggle with the interplay between large and small artery function and reflections. While wave reflection might not be a myth, the arterial pressure wave surely still carries some mysticism…
Acknowledgments
Abigail Swillens is funded by a post-doctoral grant of the Special Research Fund of Ghent University. We also acknowledge FWO-Vlaanderen for its support (research grant FWO G.0085.09).
References
Cite this article
TY - JOUR AU - Patrick Segers AU - Jonathan Mynard AU - Liesbeth Taelman AU - Sebastian Vermeersch AU - Abigail Swillens PY - 2012 DA - 2012/02/15 TI - Wave reflection: Myth or reality? JO - Artery Research SP - 7 EP - 11 VL - 6 IS - 1 SN - 1876-4401 UR - https://doi.org/10.1016/j.artres.2012.01.005 DO - 10.1016/j.artres.2012.01.005 ID - Segers2012 ER -
