Experimental verification of the healthy and atherosclerotic coronary arteries incompressibility via Digital Image Correlation
- DOI
- 10.1016/j.artres.2016.08.002How to use a DOI?
- Keywords
- Coronary artery; Atherosclerosis; Poisson’s ratio; Strain rate; Digital Image Correlation
- Abstract
So far there is no study to measure the Poisson’s ratio of the human coronary arteries in order to verify their incompressibility regardless of being healthy or atherosclerosis. It has been reported that atherosclerosis alters the elastin content of the arterial wall which is responsible for the elastic behavior of the arterial wall and helps tissue to reserve its initial shape after contracting or stretching. It is believed that the arterial walls are almost incompressible with nonlinear anisotropic mechanical response under axial or circumferential loading. Although the elastic modulus and Poisson’s ratios were both originally stemmed from the linear solid mechanics, they can be employed to address the linear elastic mechanical properties of the arterial wall under small deformation/strain. To date, many studies assumed the arterial wall as an incompressible material whether via a direct mechanical measurement or a fluid simulation study in the arterial wall, despite there is no enough supporting evidence. The present study was planned to discover this issue in detail using Digital Image Correlation (DIC) technique to lively measure the induced strains of 9 healthy and 8 atherosclerotic human coronary arteries at two different longitudinal strain rates, i.e., 5 and 20 mm/min. The Poisson’s ratio of the arterial walls, thereafter, were measured as a value of transverse strain with respect to the longitudinal strain. The results revealed the mean Poisson’s ratio of 0.49098 and 0.49330 for the healthy and atherosclerotic arterial walls, respectively, under the strain rate of 5 mm/min. Furthermore, the Poisson’s ratio of 0.49156 and 0.49702 were seen in the healthy and atherosclerotic arterial walls, respectively, under the strain rate of 20 mm/min. The results well verified the incompressibility of the coronary arterial walls regardless of being healthy or atherosclerotic under the both strain rates.
- Copyright
- © 2016 Association for Research into Arterial Structure and Physiology. Published by Elsevier B.V. All rights reserved.
- Open Access
- This is an open access article distributed under the CC BY-NC license.
Introduction
Cardiovascular disease is a wide range of clinical disorders responsible for a high rate of deaths throughout the world.1 Atherosclerosis is ranked as the most hazardous shapes of the cardiovascular disease causes by dehydrated food, smoking, pollution, stress, etc., which can alter the elastin and collagen content of the arterial wall (microstructure) and, consequently, the mechanical properties of the arterial wall.2–4 Atherosclerotic plaque is also enabled to block the blood occlusion in the arteries and, as a result, invokes a significant variation not only in the hemodynamics of the blood flow but also the mechanical properties of the arterial wall.5–7
So far there are many studies have been measured the mechanical properties of the arterial wall using different mechanical approaches, such as linear,8 nonlinear isotropic9 and anisotropic10 solid mechanics via constitutive equations.11 However, the arterial tissue can be considered as an incompressible material which is in common among almost many of the studies have been conducted so far. However, up to now there is no agreement with this assumption and, therefore, there is a need to set an experimental study to confirm that. In the past, most studies considered the arterial wall as an isotropic elastic material. In characterizing the linear mechanical properties of the arterial walls several researchers have employed the postulation of arterial walls’ incompressibility.12,13 Although this assumption may significantly abridge the mechanical behavior of the arterial wall, this would provide a more simplified mechanical behavior of the arterial wall with fewer constants, such as elastic modulus as well as Poisson’s ratio. In addition, so far there is no experimental evidence to prove the incompressibility of the human coronary arterial wall. Lawton et al.14 showed that the aortic strips were behaved like an incompressible material under different stretch ranges. The canine carotid arteries were also found to be incompressible through an internal pressurization test.15 It is well known that an impeccably incompressible material under a hydrostatic stress tolerates no comparative alteration in distance among material elements. Although it would be difficult to consider a soft tissue as an incompressible material, because all materials display some degree of compressibility. However, in some especial conditions the behavior of these materials under strains can be approximated as an incompressible material. It is known that a nearly incompressible material would not show a considerable deformation and, as a result, would have the Poisson’s ratio of 0.5. That is, the value of the axial/longitudinal strain must be nearly two times of the transverse strain. Hasegawa et al.16 proposed a non-invasive ultrasound technique to experimentally measure the Poisson’s ratio of the carotid artery and abdominal aorta. Their method employed a high spatial resolution technique to measure the both in axial and radial directions of the arterial wall and their results finally reported the value of 0.46 as the Poisson’s ratio of the arterial wall. Carew et al.17 subjected a group of 11 thoracic aorta segments of the dogs to a series of internal pressure and their results reported the Poisson’s ratio of closely to 0.5. Thereafter, the longitudinal and circumferential strain of the tissues due to internal pressure were measured accurately to prove the incompressibility (Poisson’s ratio of 0.5) of the arterial wall.18,19
To this end, most studies measured the elastic modulus, computed the hyperelastic parameters, or analyzed the nonlinear anisotropic response of the arterial tissues Therefore, there is not much result on the Poisson’s ratio of these tissue under various strain rates, namely 5 and 20 mm/min. In addition, those studies measured the Poisson’s ratio mostly have been performed on the animal models. Therefore, this study was designed to explore the Poisson’s ratio of the healthy and atherosclerotic human coronary arteries via Digital Image Correlation (DIC) technique under the strain rates of 5 and 20 mm/min. The results would provide a verification for the current assumption employed by many studies on the Poisson’s ratio of the coronary arterial walls not only in the healthy but also in the diseased condition.
Materials and methods
Experimental testing and Digital Image Correlation (DIC) technique
The coronary arteries were collected during autopsy from eight healthy and nine atherosclerotic male individuals having the mean age of 38.12 ± 9.89 and 63.73 ± 16.23 years, respectively. The samples were tried to be gathered as fresh as possible with less than 5-h post-mortem to minimize the post-mortem tissue degradation. Although there is an age difference among the tissue samples, the age difference may hardly affect the amount of Poisson’s ratio among the coronary arteries. In addition, the reports in this case well stated that the age difference may not significantly affect the mechanical properties of the coronary arterial walls.8,20 In order to figure out whether the obtained tissues are healthy or atherosclerosis, picro Sirius red staining of the cap was done and the tissues were imaged using polarized light microscopy images (Olympus, Tokyo, Japan). The atherosclerotic arterial wall is presented in Fig. 1. The diameter and length of the specimens were precisely measured via a high precision digital caliper in at least ten different points to find the average thickness of the arterial wall (Insize, Munich, Germany). In order to minimize the degradation of the arterial tissues after removal from the human body, the arterial samples once harvesting were stored in solution of 0.90% w/v of NaCl at 4–5 °C.21,22 In addition, in order to provide a humid condition for the samples, physiological solution constantly sprayed on the samples. Furthermore, to minimize the slipper effect of the jaws of the machine, a pair of coarse sandpapers glued to the lower and upper grippers of the machine. Finally, the load was longitudinally applied to the arteries until the failure occurred. The reason was that due to the dimension of the tissues it was not plausible for us to fix the strips in the transversal direction and, as a result, we could not apply such load on the arterial walls. However, since we benefitted from three high speed CCD cameras, we were able to have a thorough outlook on the response of the markers pasted to the tissue in all directions of the in-plain.

The SEM image of an atherosclerotic arterial wall. The lumen and plaque parts are distinguished in this image.11
The strain/deformation of the samples during the test was measured through DIC technique. A pair of small quadrilateral markers attached to the arterial walls. DIC is an optical/image processing technique that allows recognition of the marker displacement during the test by comparing two images, one named as reference image and the other one as deformed image. Although most previous applications of Two-Dimensional (2D) DIC for the biological materials have been bound to almost rigid tissues i.e., bone, cartilage, and hoof,23,24 very few studies recently have employed the application of 2D DIC to calculate the biomechanical characteristics of arteries, including a quick-drying high contrast speckle pattern to calculate the elastic modulus and Poisson’s ratio of a plain bovine thoracic aorta.25,26 The experimental set up is shown in Fig. 2. The uniaxial testing machine was equipped with 50 kgf load cell. The samples were mounted between the fixed and movable jaws. The movable jaws were moved upward with the speed of 5 and 20 mm/min. The transverse (X) and longitudinal (Z) displacements of the two DIC points on the arterial walls were recorded to calculate the Poisson’s ratio of the healthy and atherosclerotic coronary arteries. The light source of CCD cameras was also illuminated the surface of the objects homogeneously and helped to have a clear look of DIC points. DIC method was carried out using a group of three Charged Coupled Device (CCD) high speed video camera (Sony Corporation, Tokyo, Japan).27 The video cameras enabled to capture 280 frame/second with the resolution of 2048 × 1088 pixels which deliver a set of precise data of DIC markers’ locations. The Simi Motion® 2D/3D (Simi Reality Motion Systems GmbH, Max-Planck-Straße, Unterschleißheim, Germany) video camera software was also helped us to lively measure the deformation of each marker with respect to the other ones. Thereafter, according to the initial length of the samples we were able to calculate the strain in all data points and, thereafter, the Poisson’ ratio according to the equations that will be shown in next section. An initial (reference/undeformed) and deformed locations of the x and x* as well as the y and y* of the DIC markers on the tissue wall were defined via the matrixes F(x,y) and F*(x*,y*), respectively. The relation between these two locations on the tissue wall can be defined using the following maximum correlation parameter (C)28:
The symbol < > in Eq. (1) defines as the average quantity of the elements in the matrix. The Newton–Raphson method was employed to solve the above equations.29
After setting up the DIC devices, the coronary artery tissues subjected to quasi-static loading through a uniaxial tensile test machine until failure.30 In addition, a set of preliminary loads was applied to the samples to evaluate their need on load preconditioning. Our testing outcomes (data not reported) have revealed that conditioning of the arterial samples can be realized after 10 cycles. Hence, ten cyclic preconditioning based on the tissue behavior results before later measurements. Tensile load at the strain rate of 5 and 20 mm/min was next applied to each arterial wall.31,32 The ethical process of this study was all under the agreement/permission of the Legal Medicine Organization (LMO) based on 2008 Declaration of Helsinki.

Right after removal of the heart from the cadavers, the long-branchless coronary arteries were carefully excised from the heart, cleaned from the surrounding tissues, and kept in PBS until the mechanical test starts. After that (a) the samples were mounted between the jaws of the uniaxial testing machine and subjected to the strain rate of 5 and 20 mm/min. The (b) testing setup was consisted of a 50 kgf load cell and a pair of flat stainless steel jaws with coarse sandpapers to minimize the slippage of the samples in the jaws. The displacement/strain of two marker points on the arterial wall was lively recorded at two directions, including X and Z, by a group of three CCD cameras. Since the width of the arterial strip was not high, the DIC points were located in the lateral sides of the strips to be able to capture the deformation of the points in the z and x axes in detail. The outcomes were then reported as the displacement of these two points in the x and z direction compared to their reference locations.
Poisson’ ratio
The main objective of this study was to measure the Poisson’s ratio of the healthy and atherosclerotic coronary arterial walls. In the mechanics of the solids, the Poisson’s ratio was defined as the most typical and basis characteristics of a material which is subjected to whether the axial or compressive tensile load. It is, therefore, defined as the strain variation in the transverse direction in respect to the strain variation in the axial one. Hence, the form of the equation in this case will be:
A linear elastic isotropic material would have the Poisson’s ratio in the range of −1.0 to 0.5. Incompressible material, such as soft biological tissues, as showed small strain/deformation within the elastic region of loading would display the Poisson’s ratio of close to 0.5.
Statistical analysis
Experimental data were first examined via variance differentiation (ANOVA), and if statistical alterations were found, student’s t-test would be carried out through the SPSS software version 16.0 (SPSS Inc., Chicago, IL, the United States). Data are conveyed as mean ± std at a significance level of p < 0.05.
Results and discussions
The healthy and atherosclerotic human coronary arteries were subjected to quasi-static axial strain rates (5 and 20 mm/min) and the strain/deformation of the arterial wall was measured experimentally using a set of three CCD cameras. The X and Z displacement of the healthy and atherosclerotic coronary arteries at two different strain rates, i.e., 5 and 20 mm/min, were lively measured versus time and plotted in Fig. 3. The X stands as the transverse direction and the Z stands as the longitudinal direction. The Poisson’s ratio of the healthy and atherosclerotic human coronary arteries was then calculated as the transverse strain with respect to the longitudinal direction. The comparative histogram representation of the Poisson’s ratio of the healthy and atherosclerotic arteries at two different strain rates, including 5 and 20 mm/min, is indicated in Fig. 4. The results revealed the mean Poisson’s ratio of 0.49098 ± 0.00011 and 0.49330 ± 0.00018 for the healthy and atherosclerotic arterial walls, respectively, under the strain rate of 5 mm/min. Furthermore, the Poisson’s ratio of 0.49156 ± 0.00019 and 0.49702 ± 0.00010 were seen for the healthy and atherosclerotic arterial walls, respectively, under the strain rate of 20 mm/min. The difference is not significant, however, slightly higher in atherosclerotic artery. In addition, although there is a small decreasing in the X displacement of the markers (Fig. 3a), there is an increasing in the Z displacement of the markers in the wall of the healthy arteries (Fig. 3b). Regarding the atherosclerotic arterial wall, it is observed that there is no considerable variation in the X displacement of the markers (Fig. 3c), however, there is a substantial increasing of the Z displacement of the markers in their walls (Fig. 3d). So far there was a lack of knowledge of the Poisson’s ratio of the healthy and atherosclerotic human coronary arteries under different strain rates, the results of the present study may provide a set of suitable validation for the assumption of the incompressibility of the arterial walls not only in the healthy but also atherosclerotic states. Moreover, Poisson’s ratio is mainly a parameter of isotropy, and since in the current study the arterial wall was considered to behave like an isotropic material we enabled to measure this quantity for the arterial wall in the healthy and atherosclerotic conditions. In the current study the mechanical behavior of the arterial wall was only investigated in the linear part of the stress–strain diagram, consequently, the reported Poisson’s ratio is the one that the arterial strip showed to the Z direction applied load. Therefore, we can come up to the point that although the arterial wall is nonlinearly anisotropic, its Poisson’s ratio can be considered as an indicator of its incompressibility which has so many applications not only in the linear but also in the nonlinear isotropic behaviors of the arterial tissue. The findings of this study furthermore exhibited that both the atherosclerosis and strain rate have no significant role in the Poisson’s ratio of the arterial tissues.
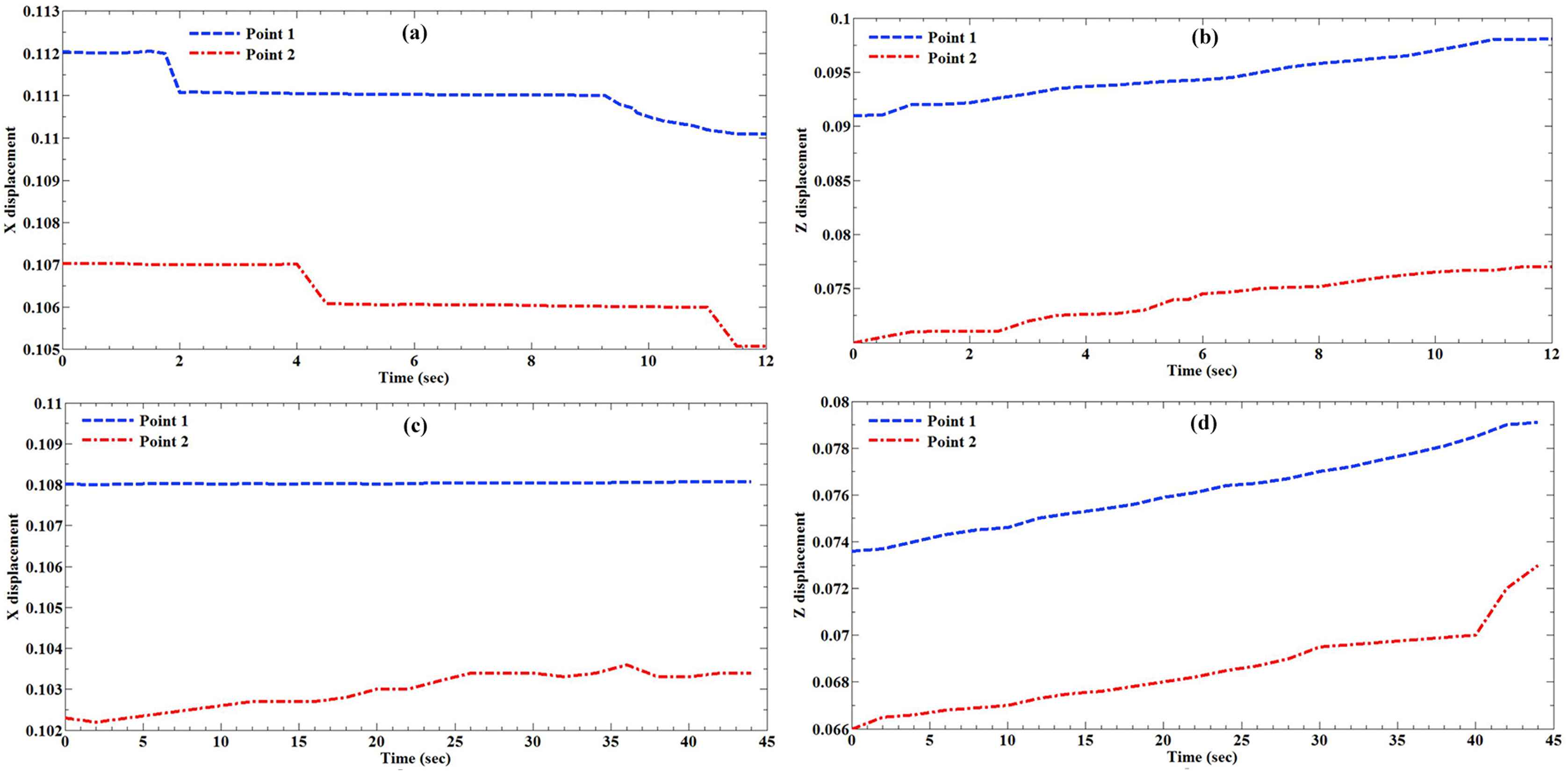
The displacement of the markers during the mechanical testing was recorded and plotted versus time. These include, the (a) X displacement (cm) and (b) Z displacement (cm) of the markers on the healthy arteries under the strain rate of 20 mm/min. In addition, (c) X displacement and (d) Z displacement of the markers on the atherosclerotic arteries under the strain rate of 5 mm/min. The locations of the markers with the numbers of 1 and 2 were displayed in Fig. 2 as well.
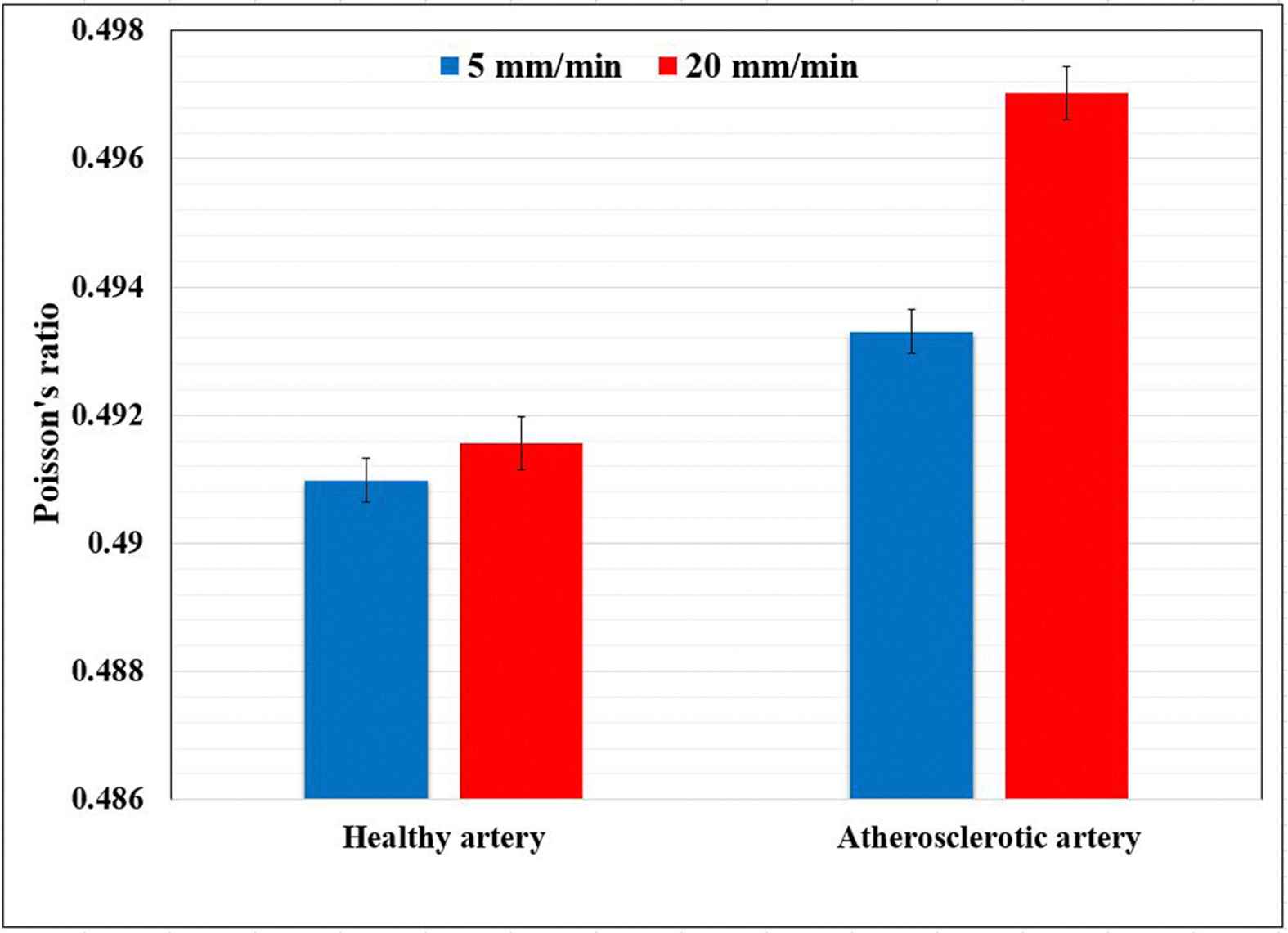
A comparative histogram representation of the healthy and atherosclerotic human coronary arteries’ Poisson’s ratio under the strain rates of 5 and 20 mm/min.
Normally, it is neither easy nor plausible to copiously evaluate the Poisson’ ratio of the healthy and atherosclerotic arterial walls at different strain rates in vivo.34,35 This study for the first time employed an optical technique to measure the Poisson’s ratio of the arterial walls under different strain rates, as 5 mm/min (slow strain rate) and 20 mm/min (fast strain rate). Although the arterial tissues were cut in a way to minimize the residual stress, its role has not been taken into account in the current study. In addition, the coronary artery was presumed to be a one-layer structure owing to the confinements of the experimental procedure, however, arterial tissue is a three layers’ structure with intima, media, and adventitia. In addition, in here the simple uniaxial tensile test was employed which stress and strains are equally applied on the thickness of the wall, however, in vivo the inner wall carries more strain and more stress that the outer wall. Therefore, in the future studies an inflation test can be carried out to shed light on this important issue of the arterial wall mechanical properties. However, the results of this study can confirm the experimental and numerical studies that assumed arterial wall as an incompressible material.36–38 Although it has previously been shown that the Poisson’s ratio of the arterial wall has no significant influence on the injury assessment of the arterial wall during plaque rupture, it would be useful if the precise value of Poisson’s ratio along with elastic modulus of the arterial wall being employed in the arterial wall model.39
Conclusions
So far there are a large amount of literatures on the supposition of the coronary arterial wall’s incompressibility, however, there is still a lack of experimental verification on that. In addition, there is no study up to now to perform a comparative study on the Poisson’s ratio of the healthy and atherosclerotic human coronary arteries under different strain rates. This study was aimed to employ the Digital Image Correlation (DIC) technique to measure the transverse strain versus longitudinal strain of the healthy and atherosclerotic human coronary arteries, in the other words Poisson’s ration, under two different strain rates, namely 5 and 20 mm/min. The results well indicated the incompressibility of the coronary arterial walls not only under various strain rates but also in two different healthy and atherosclerotic conditions. The results revealed that the Poisson’s ratio of the atherosclerotic arteries are insignificantly higher than that of the healthy ones. This might be related to the weakness of the elastin and collagen content of the atherosclerotic arterial walls which provide whether a large strain in the transverse direction or small strain in the longitudinal directions. Although in this study a combination of mechanical measurement and DIC technique were used to measure the Poisson’s ratio of the healthy and atherosclerotic of the human coronary arteries, the authors believe that their results are still promising and further research are required to consider more factors in the measurements, such as mean angle of collagen fibers, more number of markers, and biaxial mechanical testing.
Ethical issues
The use of experimental on the human body was approved by the committee of the Legal Medicine Organization (LMO) with the letter ID of 65987/253. This study was also entirely adhered to the declaration of the Helsinki in 2008.
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Conflicts of interest
None declared.
Acknowledgement
This study, including the numerical and experimental sections, was carried out in the Tissue Engineering and Biological Systems Research Laboratory of Iran University of Science and Technology under the supervision of Professor Mahdi Navidbakhsh. We thank to Professor Susumu Kudo and Professor Toshihiro Sera for their great help and time to read the manuscript and give us their comments to write the manuscript.
References
Cite this article
TY - JOUR AU - Alireza Karimi AU - Toshihiro Sera AU - Susumu Kudo AU - Mahdi Navidbakhsh PY - 2016 DA - 2016/09/01 TI - Experimental verification of the healthy and atherosclerotic coronary arteries incompressibility via Digital Image Correlation JO - Artery Research SP - 1 EP - 7 VL - 16 IS - C SN - 1876-4401 UR - https://doi.org/10.1016/j.artres.2016.08.002 DO - 10.1016/j.artres.2016.08.002 ID - Karimi2016 ER -
