Journal of Statistical Theory and Applications

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 19, Issue 2, June 2020, Pages 325 - 331

Multivariate Escher Transformed Laplace Distribution and Its Generalization

Authors
H Rimsha1, *, Dais George2
1Research and Development Center, Bharathiar University, Coimbatore; Project Fellow (UGC Major Project, Catholicate College) Pathanamthitta, Kerala, India
2Associate Professor, Catholicate College, Pathanamthitta, Kerala, India
*Corresponding author. Email: rimshahabeeb@gmail.com
Corresponding Author
H Rimsha
Received 18 November 2018, Accepted 11 December 2019, Available Online 29 July 2020.
DOI
10.2991/jsta.d.200508.001How to use a DOI?
Keywords
Autoregressive processes; Generalized multivariate Esscher transformed Laplace distribution; Geometric multivariate Esscher transformed Laplace distribution
Abstract

This paper we introduced a new distribution namely the multivariate Esscher transformed Laplace distribution. Various properties of the distribution are studied and the applications are discussed. Further we develop an autoregressive process with multivariate ETL marginal and study its properties. A Levy process based on this multivariate infinitely divisible distribution is known as Laplace motion, and its marginal distributions are multivariate generalized Esscher transformed Laplace distribution.

Copyright
© 2020 The Authors. Published by Atlantis Press B.V.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

1. INTRODUCTION

Esscher [1] introduced Esscher transformation for density approximations and later Daniels [2] and Barndorff-Nielsen [3] extended it as a general probabilistic method. Now this method is used as a means for creating a regular exponential family from a distribution whose cumulant generating function converges in the regular sense. Sebastian and Dais [4] introduced the Esscher transform of the classical Laplace distribution namely one parameter Esscher transformed Laplace (ETL) distribution and studied its various statistical properties viz infinite divisibility, geometric infinite divisibility, stability with respect to geometric summation, maximum entropy, finiteness of moments, simplicity, etc. Being heavy-tailed and asymmetric, this distribution is often used for modeling data related to various phenomena that range from image and speech recognition to ocean engineering. Some applications, extensions and generalizations of the one parameter ETL distribution is also introduced and studied (for details see, Dais and Sebastian [5,6], dais et al. [7] and Sebastian et al. [8]).

In this paper, we introduce two new distributions namely, multivariate ETL distribution and geometric multivariate ETL distribution. Autoregressive process with multivariate ETL distribution as marginal is also introduced. Generalizations of the multivariate ETL distribution and multivariate geometric ETL distribution are also considered and studied.

The probability density function and distribution function of the ETL distribution (θ), with parameter θ are

f(x,θ)=1−θ22exp[x(1+θ)],x<0 exp[−x(1−θ)],x≥0(1)
and
F(x)=(1−θ)2exp[x(1+θ)],x<0 1−θ2+1+θ2(1−exp[−x(1−θ)]),x≥0(2)
respectively, where θ∈(−1,1).

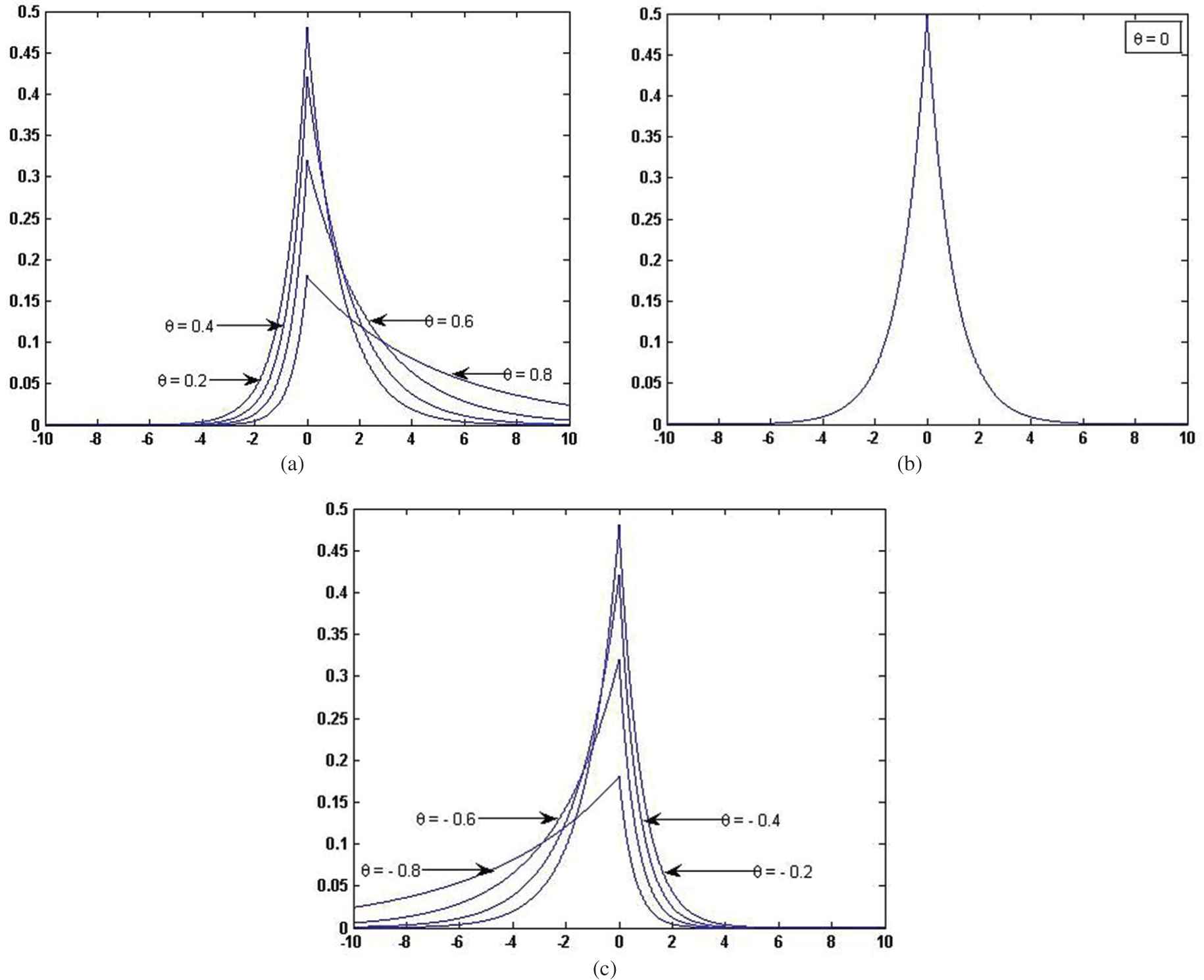
Graphs of the pdf of ETL(θ) for various values of θ are given in Figure 1.

Figure 1

Densities of Esscher transformed Laplace distribution for (a) θ∈(−1,0),(b)θ=0 (classical Laplace) and (c) θ∈(0,1)

Also the probability density function and distribution function of the location scale family of the ETL(θ) distribution denoted by ETL(θ,μ,σ) are

f(x;θ,μ,σ)=1−θ22σexpx−μσ(1+θ),x<μ,    |θ|<1,σ>01−θ22σexpμ−xσ(1−θ),x≥μ,  (3)
and
F(x)=(1−θ)2expx−μσ(1+θ),x<μ,    |θ|<1,σ>01−1+θ2expμ−xσ(1−θ),x≥μ,  .(4)

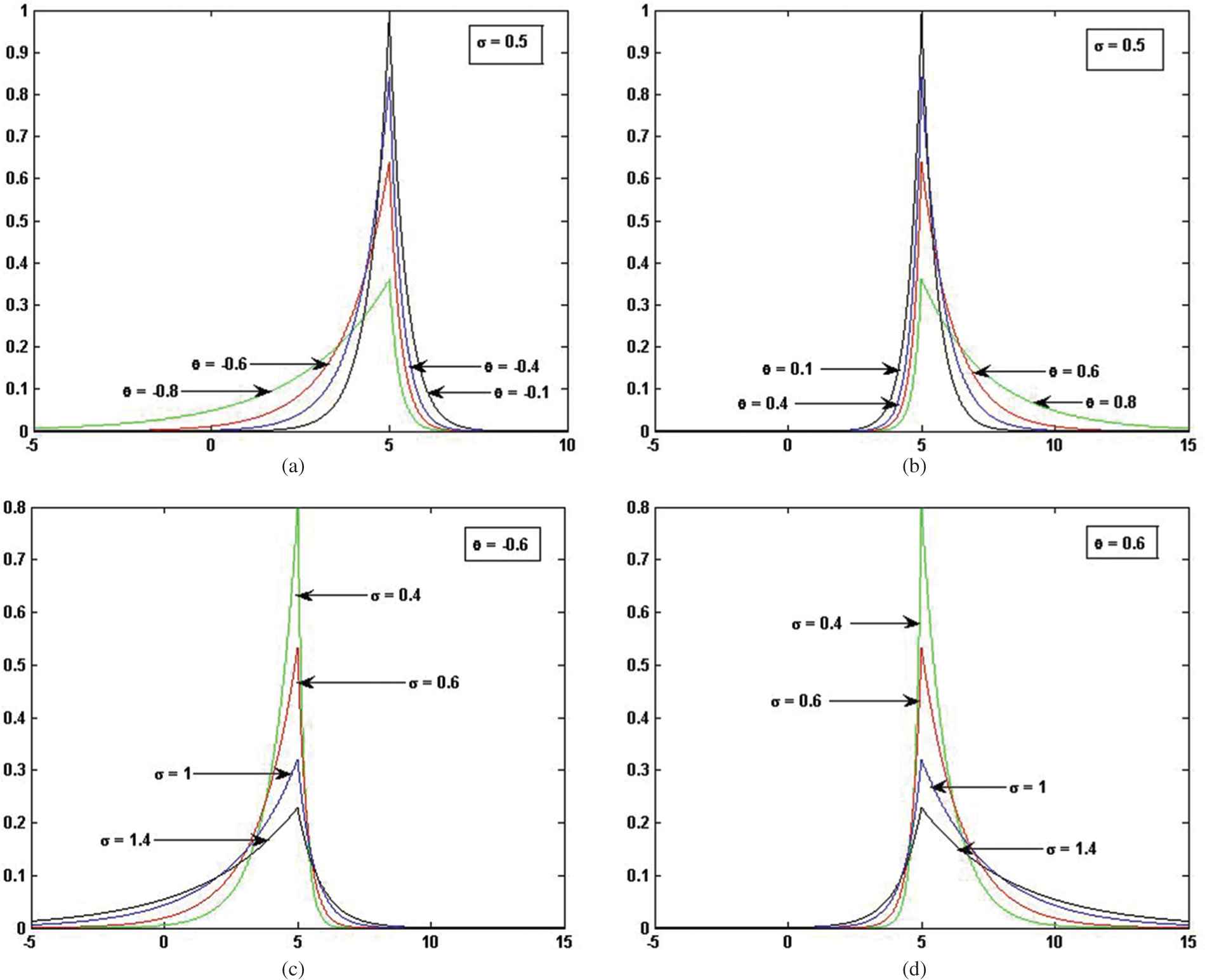
Graphs of the pdf of ETL(θ,μ,σ) for μ = 5 and for various values of θ and σ are given in Figure 2.

Figure 2

Densities of Esscher transformed Laplace distribution for (a) σ=0.5 and θϵ(−1,0), (b) σ=0.5 and θϵ(0,1), (c) θ=−0.6 and various values of σ and (d) θ = 0.6 and various values of σ.

It is clear from the graph that the distribution is asymmetric and heavy-tailed. The ETL(θ,μ,σ) distribution is left heavy-tailed, when θ is negative and right heavy-tailed when θ is positive. The distribution becomes leptokurtic and platykurtic according as σ decreases or increases.

The remaining part of the paper is as follows: In Section 2, multivariate ETL distribution, its properties and the corresponding autoregressive processes are studied. Generalized multivariate ETL distribution is discussed in Section 3 and geometric multivariate ETL distribution and its generalization is considered in Section 4. Some applications of the distributions are discussed in Section 5.

2. MULTIVARIATE ETL DISTRIBUTION

In this section, we consider the multivariate extension of the ETL distribution. The characteristic function of the ETL distribution is

ϕXθ(t)=eitμ1−2itθσ1−θ2+t2σ21−θ2(5)
so that the characteristic function of the multivariate ETL distribution denoted by ETLp(θ,Σ) is
φ(t)=11+t′Σt−2iθ′t,tϵℜd.(6)

So the probability density function of ETLp(θ,Σ) can be expressed as

f(y)=2eθ′Σ−1θ(Π)p2|Σ|12y′Σ−1y2+θ′Σ−1θ12Kv(2+θ′Σ−1θ)(y′Σ−′y)(7)
where v=2−p2 and Kv(u) is the third kind modified Bessel function.

Since ETL distribution is the scale-location mixtures of normal distributions, if X∼ETLp(θ,Σ), Y∼Np(0,Σ) and Z an exponentially distributed r.v. with mean 1, independent of Y, then the Multivariate ETL random variable X satisfies the representation

X=dθZ+ZY.(8)

If X∼ETLp(θ,Σ), then X=dY(Z), where Y s a p-dimensional Gaussian process with independent increments, Y(0) = 0 and Y(1)∼Np(0,Σ). That is, all ETL random variables can be interpreted as values of a subordinated Gaussian process.

2.1. Properties

Some important properties of the multivariate ETL distribution are discussed here.

P1. Infinite Divisibility

The characteristic function of the multivariate ETL distribution can be written in the form

φ(t)=11+t′Σt−2iθ′t1nn(9)
and hence it is infinitely divisible.

P2. Stability

Let Y,Y(1),Y(2)… be i.i.d. r.v.s in ℜp with finite second moments and γp be a geometrically distributed random variable independent of the sequence {Y(i)}. For each pϵ(0,1), the random variable Y has the stability property aPΣj=1γp(Yj+bp)→dY with ap>0, bpϵℜp iff Y is ETLp(θ,Σ) with either Σ=0 or θ=0. The normalizing constants are necessarily of the form ap=p12 and bp=0.

2.2. Multivariate ETL Processes

Because of the wide applicability of time series models with non-Gaussian marginals in various fields such as biological, engineering, telecommunications, etc., many researchers are concentrating on introducing time series models with non-Gaussian univariate and multivariate marginals. For more reference see, Jose and Seethalekshmi [9], Alexandre Trindade et al. [10], Jayakumar and Kuttikrishanan [11], Dais et al. [7] and Asma Mustafa et al. [12].

In this section, we consider first order autoregressive model (linear additive) given by

Xn=aXn−1+ϵn,|a|<1,n=0,±1,±2,…(10)
where {Xn} and innovations {ϵn} are independent p-variate random vectors. In terms of characteristic functions, this model can be rewritten as
ϕX(t)=ϕX(at)ϕϵ(t).(11)

Assuming stationarity, we have ϕϵ(t)=ϕX(t)ϕX(at) and hence

ϕϵ(t)=a2+(1−a2)1(1+t́Σt−2iθ́t).

So the innovation sequence {εn} can be treated as a sequence of random vectors of the form

ϵn=0,withprobabilitya2LP,withprobability(1−a2),(12)
where Lp's are identically distributed multivariate ETL random variables.

Theorem 2.1.

The multivariate ETL process is stationary with ETLp(θ,Σ) marginals.

Proof:

By method of induction, we can prove the result as follows:

Assume that Xn∼ETLp(θ,Σ), then

ϕXn(t)=ϕXn−1(at)ϕϵn(t) =11+a2t′Σt−2ia2θ′ta2+(1−a2)1(1+t́Σt−2iθ́t) =11+t′Σt−2iθ′t(13)
which is the characteristic function of ETLP(θ,Σ). Therefore {Xn} is strictly stationary with ETLp(θ,Σ) marginals.

2.3. Distribution of Sums and Joint Distribution of (Xn,Xn−1)

The distribution of sums Tr of the ETLp process can be obtained from the stationary sequence {Xn} satisfying (10) as

Tr=Xn+Xn+1+…+Xn+r−1=∑j=0r−1ajXn+ar−j−1ϵn+1+ar−j−2ϵn+2+…+ϵn+j=1−ar1−aXn+∑j=1r−11−ar−j1−aϵn+j.

Then

ϕTr(t)=ϕXn1−ar1−a∏j=1r−1ϕϵ1−ar−j1−at=1+1−ar1−at′Σt−2iθ′1−ar1−at−1∏j=1r−1a2+(1−a2)11+1−ar1−at′Σt−2iθ′1−ar1−at.

By inverting ϕTr(t), we can find the distribution of Tr.

The joint distribution of (Xn,Xn+1) of the multivariate ETL process can be given in terms of bivariate characteristic function as

ϕXn,Xn+1(t1,t2)=ϕXn(t1+at2)ϕϵn+1(t2) =1+(t1+at2)′−2iθ′(t1+at2)−1  a2+(1−a2)1+t2′Σt2−2iθ′t2−1.

That is, ϕXn,Xn+1(t1,t2)≠ϕXnϕXn+1(t2,t1) and hence the process, ETLP(θ,Σ) AR(1) process is not time reversible.

3. GENERALIZED MULTIVARIATE ETL DISTRIBUTION

In this section, we consider a generalization of the multivariate ETL (ETLp) distribution, namely generalized multivariate ETL (GETLp) distribution. A random vector in ℜd is said to have a generalized multivariate ETL distribution if its characteristic function is given by

φ(t)=11+t′Σt−2iθ′td,tϵℜd(14)
where d>0,θ⊂ℜd and Σ a d×d nonnegative definite symmetric matrix. This distribution is denoted by GETLp(Σ,θ,d).

Remark 3.1

If Y∼ETLp(θ,Σ), then X=dY(Z), where Y is a p-dimensional Gaussian process with independent increments, Y(0)=0 and Y(1)∼Np(θ,Σ). Since ETL distribution is infinitely divisible, define a Levy process on [0, 1) with independent increments, the Laplace motion X(d);d≥0, where X(0)=0,X(1)∼ETL(θ,Σ) and the c.f. of X(d) being

φ(t)=11+t′Σt−2iθ′td,tϵℜd.(15)

Distributions on ℜd given by (15) are called generalized multivariate ETL distributions, which we denote as GETLp(θ,Σ,d). For p=1, we obtain the Bessel function distribution.

Remark 3.2

A generalized multivariate ETL random variable admits mixture representation (8) where Z has a gamma distribution with the density

g(z)=1Γ(s)e−zzs−1.(16)

The density corresponding to (15) can be expressed in terms of Bessel function as

f(y)=2eθ′Σ−1z(Π)p2|Σ|12Γ(s)Q(z)C(Σ,θ)s−p2Ks−p2(Q(z)C(Σ,θ))(17)
where Q(z)=z′Σ−1z and C(Σ,θ)=2+θ′Σ−1θ.

4. GEOMETRIC MULTIVARIATE ETL DISTRIBUTION AND ITS GENERALIZATION

From the recent related studies, we can see that geometric classes of distributions have wide variety of applications in the field of reliability, insurance mathematics, biological sciences and engineering. So we just find out the characteristic functions of both geometric multivariate ETLdistribution, denoted by Geometric ETLp(θ,Σ) and multivariate geometric generalized ETL distribution, denoted by GGETLp(θ,Σ,d). The characteristic functions are

φ(t)=11+ln(1+t′Σt−2iθ′t),tϵℜd(18)
and
φ(t)=11+dln(1+t′Σt−2iθ′t),tϵℜd(19)
respectively and hence a geometric multivariate ETL random variable and multivariate geometric generalized ETL random variable can be generated.

Theorem 4.1.

Let X1,X2,… are i.i.d. GGETLp(θ,Σ,d) random vectors and N be geometric with mean 1p, such that P[N=k]=p(1−p)k−1,k=1,2,…,0<p<1. Then Y=X1+X2+…+XN is distributed as GGETLpθ,Σ,dn.

Theorem 4.2.

Generalized geometric multivariate ETL distribution is the limit distribution of geometric sum of random vectors following GGETLpθ,Σ,dn.

5. APPLICATIONS

In this article, we introduce some new asymmetric and heavy-tailed distributions, namely multivariate ETL distribution [ETLp(θ,Σ)], generalized multivariate ETL distribution [GETLp(θ,Σ)], geometric multivariate ETLdistribution [geometric ETLp(θ,Σ)] and generalized geometric multivariate ETL distribution [GGETLp(θ,Σ)]. The autoregressive process with multivariate ETL distribution as marginal is also developed and studied. Most of the data sets especially from finance, biological studies, Web servers and signal processing that we consider now a days are big data sets and seemed to be asymmetric and heavy-tailed. Moreover the variable that we consider in these data sets are distributed with ETL distribution and are related to other ETL distributed variables. The models developed here can also be used for modeling multivariate time series data from financial contexts. For details, see the following literature. In Sebastian George and Dais George [4], we considered the exchange rate of a particular currency say U.S. dollar with respect to Indian rupee only. Now we can use the newly introduced these distributions to study the exchange rate of U.S. dollar with respect to various currencies like Indian rupee, pound, euro, riyal, etc. at the same time. Since most of the investors have to consider the prices of different stocks at a particular time for optimal investment, this study is much important in financial contexts.

Similarly in Dais et al. [7], we consider the data sets, differences in flood levels per hour of Achenkovil river between two stations of Pathanamthitta district. Here also the multivariate distributions now developed can be used to study flood levels per hour of Achenkovil river between different stations in adjacent geographic zones so that the complexity of problems associated with water management faced by the State of Kerala due to the high variations in spatial and temporal rainfall can be made under control. Again in Dais George and Sebastian George [5], we model the file size distribution of Web server data with the ETL distribution and we know that many data sets related with Web servers (which are interrelated also) are asymmetric and heavy-tailed and can be modeled with ETL distribution. The geometric classes of distributions also have wide variety of applications in the field of reliability, insurance mathematics, biological sciences and engineering. As such all the newly introduced distributions are more useful and tactable.

CONFLICT OF INTEREST

No conflict of interest to declare.

REFERENCES

4.S. George and D. George, J. Probab. Stat. Sci., Vol. 10, 2012, pp. 135-152.
5.D. George and S. George, J. Digit. Inf. Manag., Vol. 9, 2011, pp. 19-26.
7.D. George, S. George, and H. Rimsha, Far East J. Theor. Stat., Vol. 52, 2016, pp. 455-483.
8.S. George, D. George, and L. George, J. Probab. Stat. Sci., Vol. 14, 2016, pp. 29-44.
9.K.K. Jose and V. Seethalekshmi, J. Stat. Stud., Vol. 23, 2003, pp. 33-37.
10.T.A. Alexandre, Z. Yun, and A. Beth, J. Stat. Comput. Simul., Vol. 9, 2009, pp. 1563-1588.
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
Journal of Statistical Theory and Applications
Volume-Issue
19 - 2
Pages
325 - 331
Publication Date
2020/07/29
ISSN (Online)
2214-1766
ISSN (Print)
1538-7887
DOI
10.2991/jsta.d.200508.001How to use a DOI?
Copyright
© 2020 The Authors. Published by Atlantis Press B.V.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - H Rimsha
AU  - Dais George
PY  - 2020
DA  - 2020/07/29
TI  - Multivariate Escher Transformed Laplace Distribution and Its Generalization
JO  - Journal of Statistical Theory and Applications
SP  - 325
EP  - 331
VL  - 19
IS  - 2
SN  - 2214-1766
UR  - https://doi.org/10.2991/jsta.d.200508.001
DO  - 10.2991/jsta.d.200508.001
ID  - Rimsha2020
ER  -