Selective synchronization of coupled bifurcating neurons for phase shift of background oscillation
- DOI
- 10.2991/jrnal.2018.5.2.1How to use a DOI?
- Keywords
- chaotic synchronization; neural coding; bifurcating neuron; binding information
- Abstract
Synchronization in coupled bifurcating neurons was studied from the view point of the selective formation of cell assembly. The bifurcating neuron is a simple chaotic neuron that exhibits chaotic inter-spike interval dynamics via the addition of sinusoidal background oscillation. In this research, we introduced the phase shift of the background oscillation and several types of phase response to the input spike sequence. Sixteen coupled bifurcating neurons with complete bidirectional coupling were numerically simulated and their synchronized behaviors were analyzed. As a result, the formation of chaotically synchronized cell assemblies for the phase shift value were observed.
- Copyright
- Copyright © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Synchronized neural activity has an important role in neural information coding and brain information processing1. The correlated firing among neurons has been observed in visual information processing in the brain2,3. The authors have studied the chaotic synchronization of the neural spike response and its application to the segmentation of input images4; feature linking of the visual image of moving objects5; and the decomposition of superimposed chaotic spike sequences6. In order to represent multiple information by chaotic synchronized cell assemblies, confirming the coexistence of synchronized assemblies is necessary.
In this study, we constructed the network of the bifurcating neuron7 with complete bidirectional coupling and designed a coupling model to achieve selective chaotic synchronization based on the phase response. In Sections 2 and 3, we explain the bifurcating neuron network and coupling model. In Section 4, we describe the numerical simulation that is performed to examine the selective synchronization for the phase shift of the background oscillation. We summarize the results in Section 5.
2. Network model of the bifurcating neuron
The bifurcating neuron was introduced by Lee and Farhat7. In our previous research6, we defined the bifurcating neuron as a form of the spike response model8 to extend the coupling term based on the phase response. In the following sections, we explain the extended bifurcating neuron model and its network. Let the network of bifurcating neurons consist of N neurons, where n(i) is the i-th neuron. The dynamics of the i-th bifurcating neuron is defined as follows:
The kernel function η(i) is defined as
The dynamics of a single neuron without the coupling term is the same as with the original bifurcating neuron. The single neuron without coupling exhibits various chaotic dynamics in the inter-spike interval, and the phase of the next firing time is determined by the chaotic one dimensional map of the phase of the last firing time6,7. The shape of this chaotic map is determined by the phase shift value, ϕ(i). Examples of this chaotic map are shown in Fig. 1. Furthermore, the bifurcation diagram and Lyapunov exponents of this map are shown in Fig. 2.
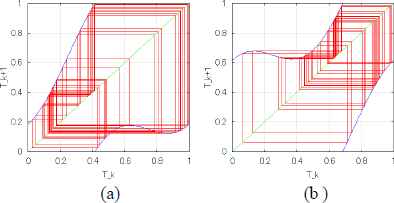
Examples of the chaotic one dimensional map of the phase of a single bifurcating neuron with the phase shift (a) ϕ = π/2 and (b) ϕ = 3π/2.
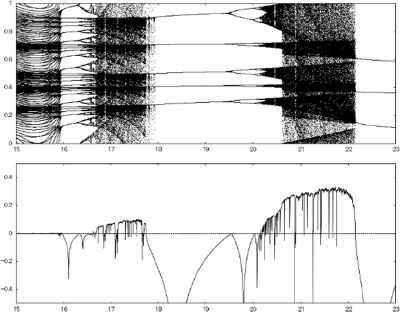
The bifurcation diagram and Lyapunov exponents of a single bifurcating neuron without coupling.
3. Coupling model with phase response
Let the set
We designed the phase response to strengthen the chaotic synchronization between coupled neurons with the same phase shift value6. The positive phase response based on the predicted next firing time is defined as
If time, s, is within the range, Δε, from the predicted next firing time
4. Numerical experiments
4.1. Experimental setting
We numerically simulated a network of 16 bifurcating neurons to analyze the selective synchronization to the same phase shift value for complete bidirectional coupling. We assigned 4 different phase shift values, as follows:
4.2. Characteristics of synchronization
As an index of synchronization between two spike sequences, the synchronization ratio was defined as
4.3. Experimental results
An example of our generated spike sequences from the numerical simulation are shown in Fig. 3, where the phase response coupling is the adaptive positive and negative coupling. The generated spikes were synchronized for each 4 neurons using the same phase shift value, and selective synchronization for the same phase shift value was observed. We numerically simulated the network and evaluated the synchronization ratio to analyze the effect of coupling, and the mean ratio for each of the 5 types of coupling that were defined in Section 3. Results are shown in Fig. 4 and Table 1. These results indicated that selective synchronization was observed for coupling types (c) and (e). The mean synchronization ratios were greater than 90% for the neurons with the same phase shift value, and less than 40% for the neurons with the different phase shift values.
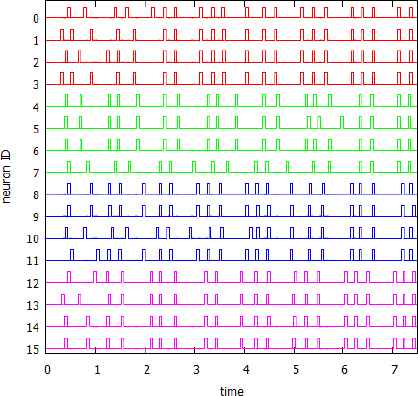
An example of generated spike sequences for the network with the adaptive positive and negative coupling.
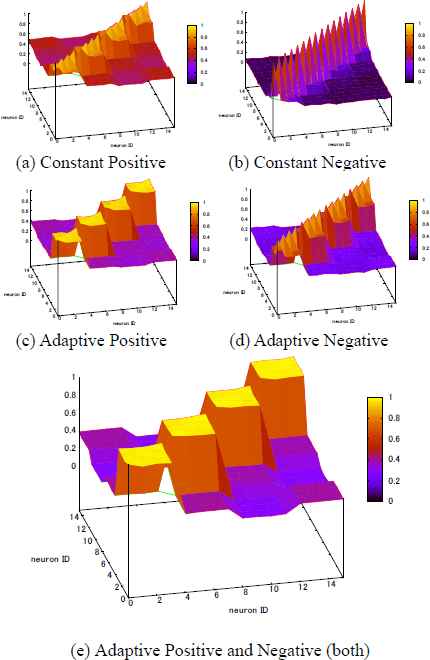
The synchronization ratio between two neurons for (a) Constant Positive, (b) constant negative, (c) adaptive positive, (d) adaptive negative, and (e) both adaptive positive and negative coupling types.
| Coupling type | MSRϕ(i)=ϕ(k) | MSRϕ(i)≠ϕ(k) |
|---|---|---|
| (a) Constant Positive | 0.7861 | 0.4766 |
| (b) Constant Negative | 0.1819 | 0.0638 |
| (c) Adaptive Positive | 0.9414 | 0.3694 |
| (d) Adaptive Negative | 0.6520 | 0.2057 |
| (e) Adaptive Positive and Negative | 0.9723 | 0.3519 |
Mean synchronization ratio for the neurons with the same phase shift value, MSRϕ(i)=ϕ(k), and for the neurons with the different phase shift values, MSRϕ(i)≠ϕ(k).
5. Conclusion
We have constructed a bifurcating neuron network, and assessed the formation of chaotically synchronized cell assemblies for several types of coupling model. As a result, the chaotically synchronized cell assemblies were observed for adaptive positive coupling of the phase response, where neurons that have the same phase shift value were selectively synchronized. This result indicates the possibility of binding information based on the phase shift value of the background oscillation. Our future work will seek to analyze the effect of adaptive coupling using a different chaotic neuron model, which will further elucidate such information coding.
Acknowledgements
This work was partially supported by MEXT KAKENHI Grant Number 15H05878 and 16K00409.
References
Cite this article
TY - JOUR AU - Akihiro Yamaguchi AU - Yutaka Yamaguti AU - Masao Kubo PY - 2018 DA - 2018/09/30 TI - Selective synchronization of coupled bifurcating neurons for phase shift of background oscillation JO - Journal of Robotics, Networking and Artificial Life SP - 79 EP - 82 VL - 5 IS - 2 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.2018.5.2.1 DO - 10.2991/jrnal.2018.5.2.1 ID - Yamaguchi2018 ER -
