Design of a Performance-Adaptive 1-Parameter Tuning PID Controller
- DOI
- 10.2991/jrnal.k.190531.007How to use a DOI?
- Keywords
- PID control; data-oriented; self-tuning control; performance-driven; 1-parameter tuning
- Abstract
Many self-tuning Proportional–Integral–Derivative (PID) controllers have been proposed. However, these methods are rarely employed to actual systems because of low reliability of an on-line PID parameter estimator. In this work, a performance adaptive controller that has two stages of PID parameters tuning mechanisms is proposed. One of the tuners is a 1-parameter tuner using the recursive least squares. The other tunes PID parameters using ordinary least squares. The effectiveness of the proposed method is evaluated by an experimental example.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Most of the controllers in industries have fixed control parameters. However, the controllers cannot obtain good control performances against time-variant systems. To tackle this problem, self-tuning controllers [1,2] have been proposed. In these controllers, control parameters are tuned adaptively and can maintain a good control performance to time-variant systems. However, it is difficult to use these methods to actual systems because of low reliability of an on-line estimator. In addition, it is not preferred to tune many control parameters simultaneously in terms of the safeness of a closed-loop system.
Especially in process industries, Proportional–Integral–Derivative (PID) controllers [3] have been widely used. The reasons why PID controllers have been widely applied include that: (1) PID controllers have simple structure, and (2) physical meanings of the control actions are clear. Therefore, some self-tuning PID control schemes [2] have been proposed.
In this work, a performance-adaptive controller that has two stages of PID parameters tuning mechanisms is proposed. One of the tuners is a 1-parameter tuner which calculates only the proportional gain using the recursive least squares. The proportional gain depends only on a static gain of the controlled object, thus the reliability of an identification of the proportional gain is higher than the other gains. The other is a PID parameters tuner using ordinary least squares. When the 1-parameter tuner cannot maintain a good control performance, the PID parameters tuner determines new PID parameters to maintain a desired control performance. The effectiveness of the proposed method is evaluated by an experimental example.
2. THE TUNING METHOD OF PID PARAMETERS
The PID parameters tuning method is described at this section. A velocity-type PID controller in discrete time domain is given as follows:
Generalized output Φ(k) is defined as follows:
Where coefficients a1, a2, and a3 are defined as follows:
From (3) to (5), the following relationship can be obtained:
In the proposed method, it is desired to make the system output y(k) track the reference model output yr(k) which is defined by
The evaluation function J is defined as follows:
3. DESIGN OF A PERFORMANCE DRIVEN PID CONTROLLER
3.1. 1-Parameter Tuning
Both 1-parameter tuning and retuning of all PID parameters are realized by using the PID tuning method described at the previous section. In the 1-parameter tuning, only overall gain of the PID controller kc is tuned. From Equation (15), kc is rewritten as follows:
Furthermore, Ti and Td are constant values, and a2 and a3 are also constant values. Therefore, 1-parameter tuning can be realized by tuning only a1. In this paper, a recursive least squares method [4] is applied to minimize ε(k). Estimated parameter vector
3.2. Control Performance Evaluation
When 1-parameter tuning cannot maintain good control performance, all PID parameters should be tuned. In this subsection, the evaluation criterion of control performance is described. A reference signal is assumed to be the step-type signal. The criterion of control performance is defined as follows:
3.3. A Method of PID Parameters Tuning
In order to tune all PID parameters, the PID tuning method described at Section 2 are used. The optimized parameters are a1, a2, and a3. In addition, least squares method is used to minimize ε(k). In the ordinary least squares, the data between k0 and k steps are used.
4. AN EXPERIMENTAL RESULT
The usefulness of the proposed self-tuning method is experimentally evaluated on a pilot-scale temperature control system. Figure 1 shows an appearance of the controlled object, and the schematic figure is illustrated in Figure 2. In this experimental system, two heaters are secured on a steel plate. These heaters work synchronously, corresponding to the input signal from the computer. One thermo-couple is also prepared, and the measured temperature of the steel is sent to the computer as the system output signal. The control objective is to regulate the temperature of the steel to the desired reference signal by manipulating the power of the heater. In this experimental result, the sampling time Ts is 1 s and the reference signal is changed alternately from 70 (°C) in the temperature and 100 (°C).
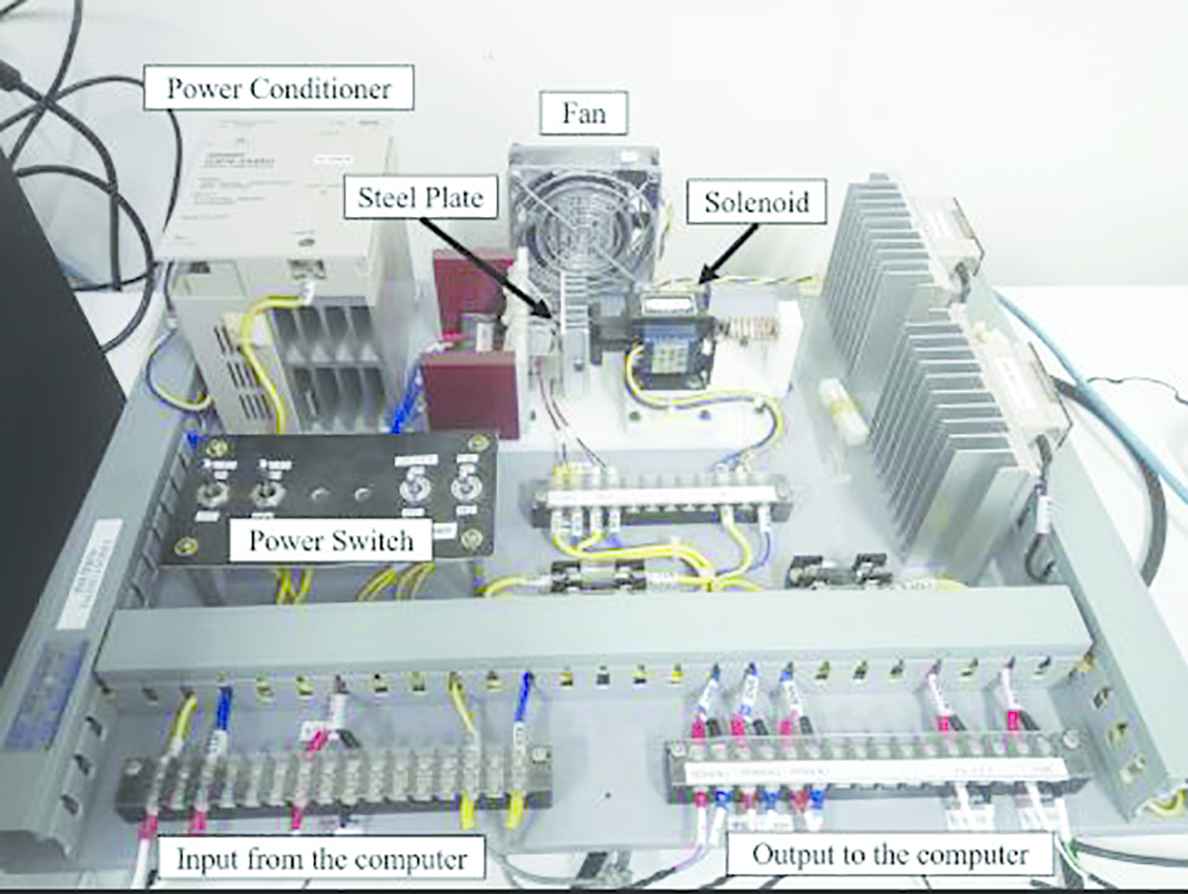
Appearance of the experimental temperature control system.
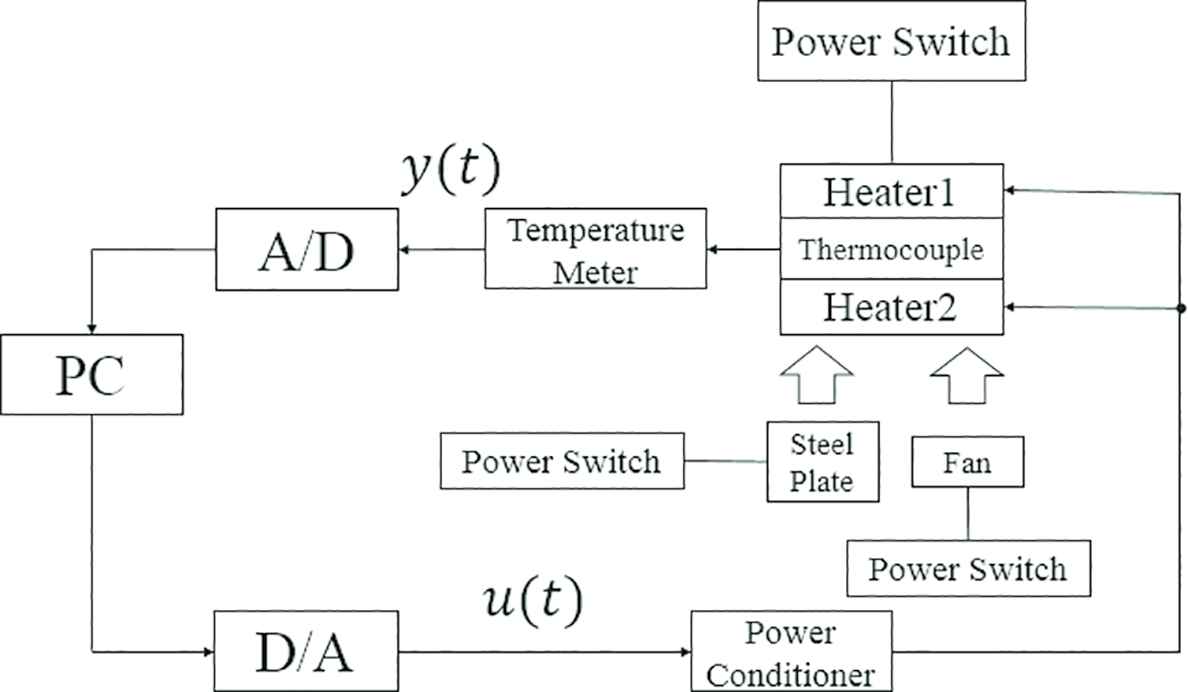
Schematic figure of the experimental temperature control system.
To simulate heater deterioration, the relationship between controlled input u(k) and the voltage of the power conditioner v(k) is varied as follows:
The control result by using the proposed performance-adaptive controller is shown as Figure 3, and the trajectories of PID parameters corresponding to Figure 3 is shown in Figure 4. In this result, the initial PID parameters were determined by using the PID tuning method described at Section 2 as follows:
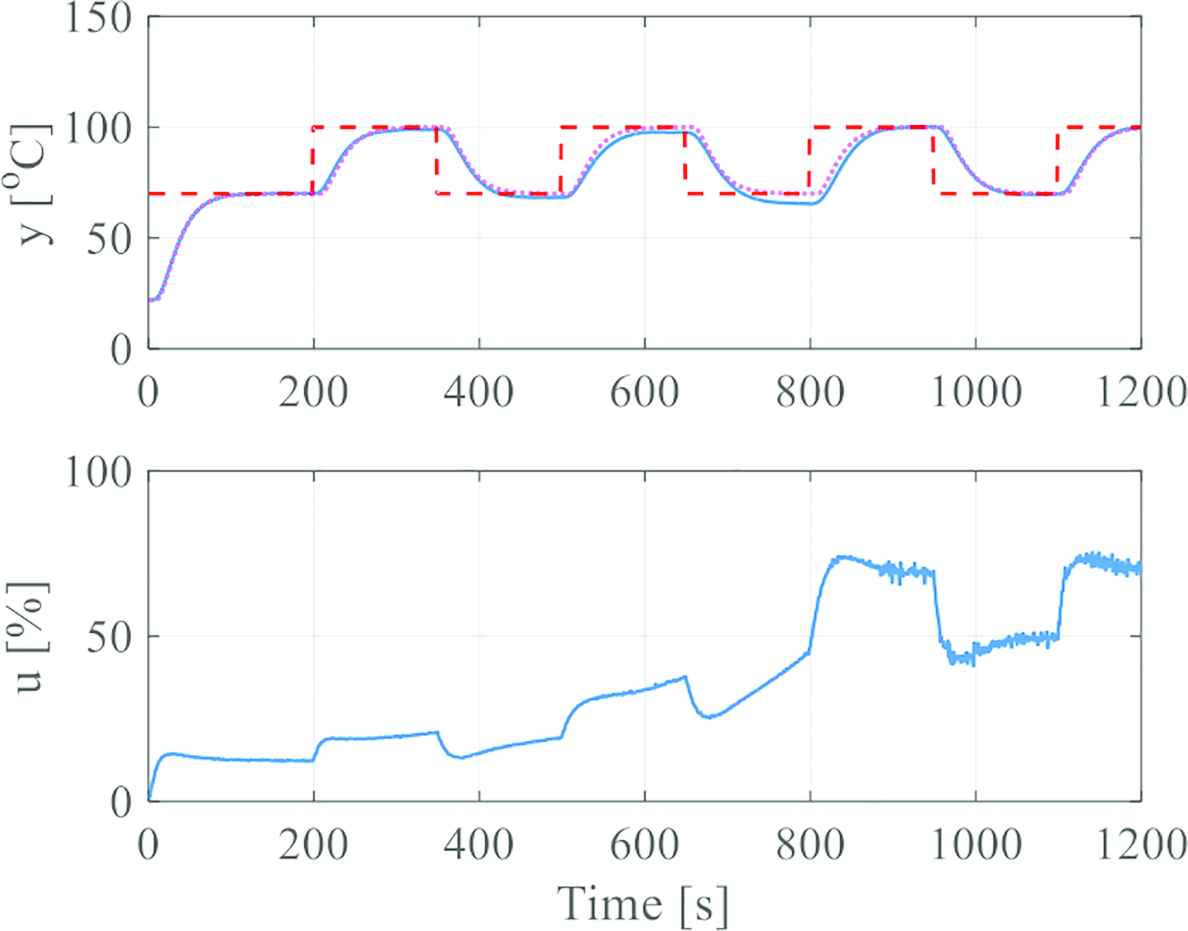
Experimental control result by using the proposed control method.
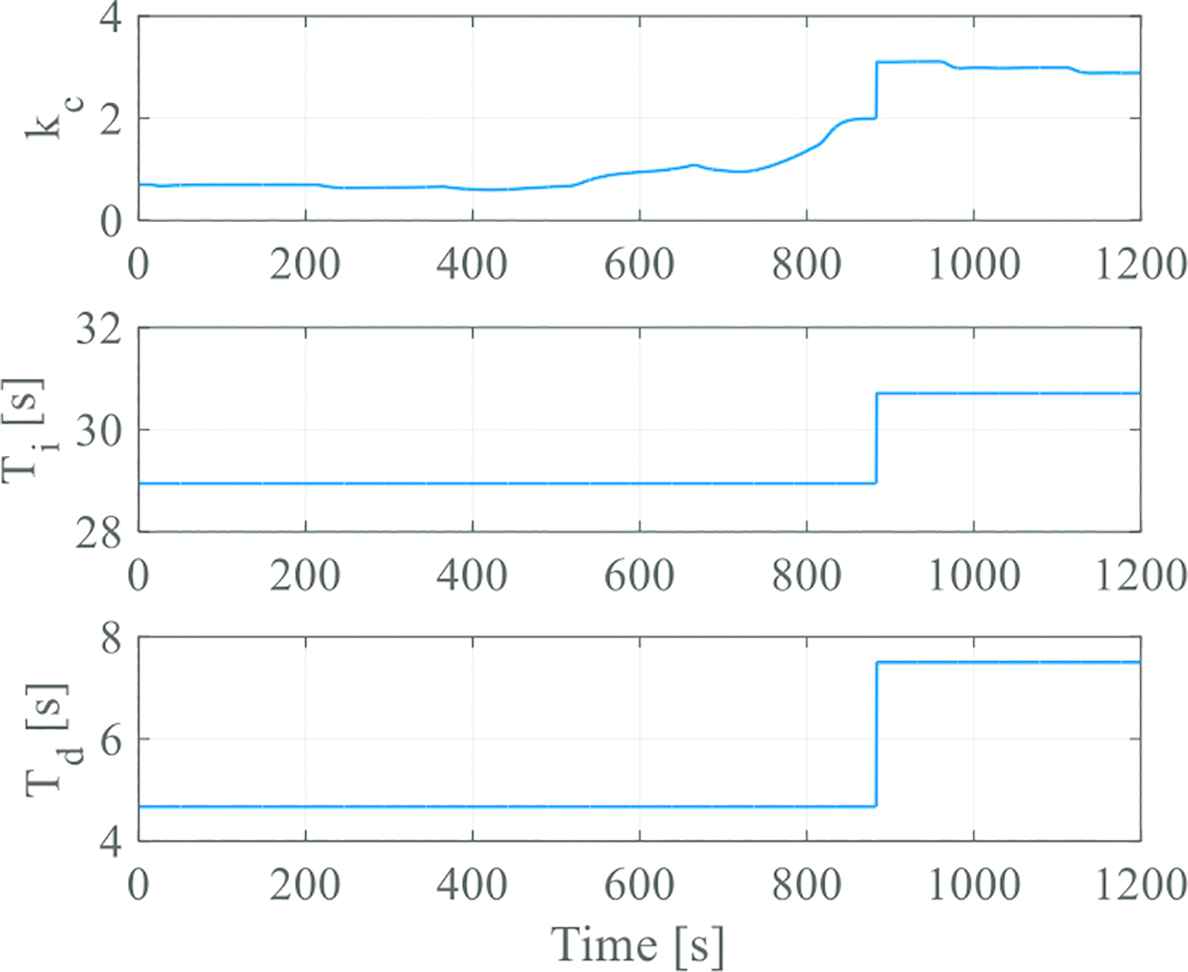
Trajectories of the PID parameters corresponding to the Figure 3.
Parameters of the proposed method were set as follows: α = 1, β = 0.2, d = 8, w(k) = 0.995, σ = 30, and δ = 0. From Equation (26), initial estimated parameter was determined as
Figure 3 indicates that the control performance gradually deteriorated after 200 steps. Figure 4 shows that only kc was tuned before 863 steps, and all PID parameters are tuned at 863 steps. The proportional gain kc became larger on the 1-parameter tuning period. Considering that the system gain became smaller on the period as Equation (25), the variation of the kc is correct. In addition, after the tuning of the all parameters, the trajectory of the control output is likely the same as the reference trajectory.
5. CONCLUSION
In this paper, a performance-adaptive 1-parameter tuning PID controller is proposed, and effectiveness of the proposed method is evaluated by the pilot-scale temperature control system. The proposed performance adaptive controller has two stages of PID parameters tuning mechanisms. The features of the proposed method are summarized as follows:
- •
The proposed method is the 1-parameter tuning method, and only kc is tuned.
- •
All PID parameters are retuned only when control performance deteriorates.
- •
Both the 1-parameter tuning and the retuning method of all PID parameters are based on the same PID tuning scheme.
CONFLICTS OF INTEREST
There is no conflicts of interest.
Authors Introduction
Dr. Yoichiro Ashida
 He received his D.Eng. degree from Hiroshima University in 2019. His main research interests are data-driven controller tuning, PID control, and delay systems. He is currently an Assistant Professor with Department of Electrical Engineering and Computer Science, National Institute of Technology Matsue College.
He received his D.Eng. degree from Hiroshima University in 2019. His main research interests are data-driven controller tuning, PID control, and delay systems. He is currently an Assistant Professor with Department of Electrical Engineering and Computer Science, National Institute of Technology Matsue College.
Dr. Shin Wakitani
 He received his B.Ed. and M.Ed. degrees from Hiroshima University in 2009 and 2011, respectively, and his D.Eng. degree from Hiroshima University in 2013. From 2013 to 2016, he was with Tokyo University of Agriculture and Technology as an Assistant Professor. He is currently an Associate Professor with Department of System Cybernetics, Graduate School of Engineering, Hiroshima University. His research interests are in data-driven controller design, performance-driven controller design, and controller design based on skilled workers’ operation data.
He received his B.Ed. and M.Ed. degrees from Hiroshima University in 2009 and 2011, respectively, and his D.Eng. degree from Hiroshima University in 2013. From 2013 to 2016, he was with Tokyo University of Agriculture and Technology as an Assistant Professor. He is currently an Associate Professor with Department of System Cybernetics, Graduate School of Engineering, Hiroshima University. His research interests are in data-driven controller design, performance-driven controller design, and controller design based on skilled workers’ operation data.
Dr. Toru Yamamoto
 He received his B.Eng. and M.Eng. degrees from the University of Tokushima, Japan, in 1984 and 1987, respectively, and the D.Eng. degree from Osaka University, Japan, in 1994. He is currently a Professor with the Department of System Cybernetics, Graduate School of Engineering, Hiroshima University, Japan. He was a Visiting Researcher with the Department of Mathematical Engineering and Information Physics, University of Tokyo, Japan, in 1991, and he was an Overseas Research Fellow of the Japan Society for Promotion of Science (JSPS) with the University of Alberta for six months in 2006. His current research interests are in the area of self-tuning and learning control, data-driven control, and their implementation for industrial systems. He was a General Chair of ADCONIP 2014 and SICE Annual Conference 2019.
He received his B.Eng. and M.Eng. degrees from the University of Tokushima, Japan, in 1984 and 1987, respectively, and the D.Eng. degree from Osaka University, Japan, in 1994. He is currently a Professor with the Department of System Cybernetics, Graduate School of Engineering, Hiroshima University, Japan. He was a Visiting Researcher with the Department of Mathematical Engineering and Information Physics, University of Tokyo, Japan, in 1991, and he was an Overseas Research Fellow of the Japan Society for Promotion of Science (JSPS) with the University of Alberta for six months in 2006. His current research interests are in the area of self-tuning and learning control, data-driven control, and their implementation for industrial systems. He was a General Chair of ADCONIP 2014 and SICE Annual Conference 2019.
REFERENCES
Cite this article
TY - JOUR AU - Yoichiro Ashida AU - Shin Wakitani AU - Toru Yamamoto PY - 2019 DA - 2019/06/25 TI - Design of a Performance-Adaptive 1-Parameter Tuning PID Controller JO - Journal of Robotics, Networking and Artificial Life SP - 33 EP - 37 VL - 6 IS - 1 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.190531.007 DO - 10.2991/jrnal.k.190531.007 ID - Ashida2019 ER -
