A Turing Machine Constructed with Cubelets Robots
- DOI
- 10.2991/jrnal.k.190220.013How to use a DOI?
- Keywords
- Turing machine; robotics; cubelets; Lego; cellular automata
- Abstract
We describe the design and implementation of a modular and distributed robot that physically simulates functioning of a 2-symbols Turing machine. The robot is constructed with Cubelets (small autonomous robot-cubes used for teaching basic robotics and programming for kids) and Lego® bricks (thus the robot is called CULET). The Cubelets robotic blocks allow for a high level programming: instead of a traditional code, the robots are programmed by assembling various elementary blocks of robots together. We illustrate how read and write operations are physically implemented by the CULET.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
In the history of Turing machines a large number of physical mechanical devices have been developed. For example, in 2012, to celebrate Turing’s 100th birthday, LEGO built an autonomous mechanical Turing machine adding binary numbers [1]. Being inspired by ideas of machines emerged from the theory of self-reproducing cellular automata [2], we decided to make a robot based in small robotic-cubes Cubelets and pieces Lego®. We called this robot CULET. A key feature of CULET is the first ever implementation of the machine constructed with robots and bricks. This robotic machine is capable for simulating the function of other machine. Cubelets, enhanced with pieces of Lego bricks, demonstrate how a robotic machine simulates an abstract computing machine. A distributed controller of the robot is in the cube which can implement operation read and other two cubes that move the head and the arm (which implements write operation). These cubes need to be re-programed for each table of transitions.
For the implementations we programmed two special Turing machines. The first one is a universal Turing machine able to simulate the behaviour of a complex elementary universal cellular automaton known as Rule 110 [3]. The second Turing machine programmed in CULET doubles the number of 1’s in the tape.
This is an extended version of a work presented at the International Conference on Artificial Life and Robotics (ICAROB), 2019 edition [4]. The subjects treated here and not in the original version are: (1) the exposition of a similar machine to CULET that is able to perform logic operations and (2) a clearer explanation of the operation of the robot.
The paper is structured as follows. In Section 2 we introduce the Cubelet robots and describe the Turing machines implemented. Section 3 describes the design. Section 4 describes the implementation of a robot that computes logic functions. We give some final remarks in Section 5.
2. PRELIMINARIES
2.1. Cubelets
The Cubelets are small cube-shaped robots designed to teach fundamentals of robotics and programming to kids. Cubes can have different functionality. An idea is to construct robots only through the concatenation of different cubes. This way Cubelets can be seen as a formal language, where every valid construction is a valid expression in the language, with virtually unlimited number of possible combinations. This can be interpreted as a high level of programming: a user does not modify the original program of each cube, but instead, uses this program together with the interaction among cubes to produce a new robot. There are three types of cubes [5]:
- •
Input sensors: cubes used to obtain data from the environment. The most common are the proximity and light sensors.
- •
Actuators: cubes used to execute movements, e.g. drives or rotors.
- •
Thinkers: cubes to implement a computation, e.g. inverters, maximum, minimum, etc.
A single cube communicates with his neighbourhoods through a shared channel that is established in the concatenation of blocks. The input sensors-cubes distribute their readings thought the channels; the thinkers-cubes obtain these readings, process the information and make a decision, and send the commands to the actuators.
Also, each cube can be reprogrammed to re-assign its functionality. This reprogramming is done in C or Scratch-like code. CULET, which is described in the next section, follows this approach.
2.2. Universal Turing Machines
The Turing machines were proposed by Turing in 1936 [6] to solve problems about completeness and decidability. A Turing machine is a finite-state machine with an external memory medium, an infinite tape divided into squares. A head of the machine moves on the tape and reads the value in each square sequentially [7]. Formally, the Turing machine is a set of quintuples of the form [Equation (1)]:
One of the greatest achievements of Turing’s work is the conceptualization of the so called universal machines. A universal machine U can do everything that any machine can do. U receives as input two things: a description of a machine A, and the input for that machine M. The machine U writes on the tape the same string of symbols that the machine A would write in its response to the input M.
2.3. Elementary Cellular Automata
Cellular automata were proposed by von Neumann [2] as means to study decentralized systems (which later led to designs of distributed computing, ironically called non-von-Neumann-style computers). The cellular automata consists of an array of cells, each of which is a finite-state automaton (the same rules for all the cells) and where the state of each cell in the next generation depends on its current neighbourhood. Von Neumann developed a very complex automaton with 29 states evolving in two dimensions.
Another important event in cellular automata history is the popularization of Conway’s Game of Life in the 70’s [9]. This is a cellular automaton with only two states and a neighbourhood of eight cells (Moore neighbourhood). The automaton is popular because it shows how a complex and unpredictable behaviour emerges from simple rules. Berlekamp et al. [10] demonstrated the universality of this automata by constructing a register machine.
In the 1980’s years, Wolfram [11] described the elementary cellular automata to understand and formalise the dynamics of cellular automata. The space is one-dimensional (a row of cells) and a cell’s neighbourhood is two closest cell-neighbours of the cell. Wolfram hypothesis was that if we cannot understand such minimal models, then we could never understand bigger ones. The interesting part comes when even in those apparently simple automata there are intriguing patterns of a behaviour.
2.4. Universal ECA: Rule 110
Cook [12] proved that the elementary cellular automaton Rule 110 is universal. The proof is based on showing how, with particle interactions [13] typical of the rule, one can emulate the operation of a cyclic tag system. This one is the smallest cellular automaton demonstrated to be computationally universal by simulating a very sophisticated sequential machine via particles collisions in one dimension. Such a new machine was invented to simulate a computable function known as a cyclic tag system in this automaton, for details see Cook [12] and Wolfram [14]. Rule 110 can simulate a cyclic tag system [12], cyclic tag systems can simulate tag systems [12,14], tag systems can simulate Turing machines [7], and a Turing machine (developed by Eppstein and published by Cook [12]) can simulate Rule 110 and therefore such a Turing machine is universal. The CULET can simulate the universal Turing machine which simulates the behaviour of Rule 110, complex behaviour, and collisions of particles [15,16].
The state diagram of Figure 1a shows the operation of the machine. Every generation in which the head of the machine reaches a right end, a new generation of the rule 110 is computed. There are some considerations with respect to this machine: the initial condition and the representation of the cellular automata symbols. The initial condition of the machine must be, from left to right, an infinite string of zeros, the encoded version of the initial configuration that the machine is going to emulate, and an infinite repetition of the string “10”. A “1” of the cellular automata is represented like “11” in the machine, and a “0” like “00”; the symbol “10” is used like a blank symbol.
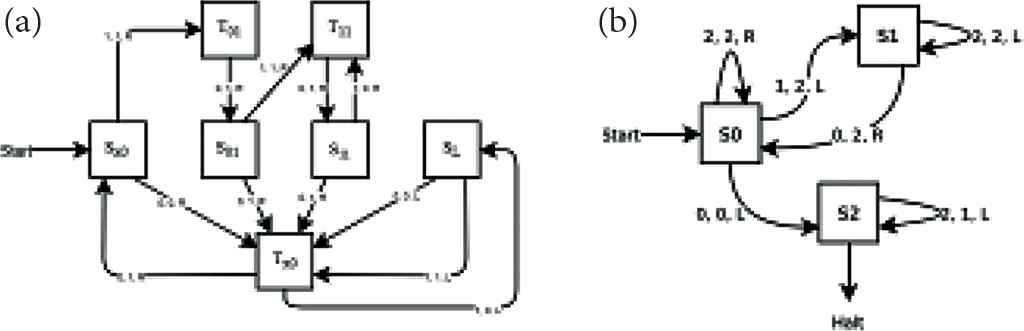
Implemented Turing machines. (a) Rule 110. (b) Duplicator.
2.5. Duplicator Turing Machine
A duplicator Turing machine was used by Rendell [17] as a part of the Turing machine constructed in the Game of Life cellular automaton. We implement this machine in CULET. In Figure 1b, we show a 3-symbols version: it starts advancing to the right, for each one scanned, it put another one in the left until there is no more ones to the right. For the implementation in the CULET we used a 2-symbols version of this machine.
3. CULET DESIGN
In Figure 2 we show a snapshot of CULET. The tape is represented by an array of Lego blocks on rectangles of a black paper; the position of the block (front or back) indicates the symbol in the cell (0 or 1, respectively). The Cubelet car moves through the tape reading and writing in the tape; the read operation is achieved with a distance sensor that tests the position of the Lego block under scanning; the writing is done with a lever made of Lego and a rotate cube: depending on the desired symbol, the lever pushes or pulls the block of the tape. The movement across the tape is done with a couple of wheels that move in right or left direction. In the backwards of the car is attached a rail that helps to maintain the alignment of the car with respect to the tape.

Robotic Turing machine.
The rotator cube plays the role of controller: it reads the values of the distance sensors, move the Lego leaver and instruct the wheels when to move and in which direction. This controller encodes the transition rules of the Turing machine being simulated. The controller program starts reading the current symbol on the tape. Depending on the value scanned, it determines if a writing operation is needed, and if is the case, it performs it. After that, the controller instructs the motor on the new direction to move, left or right, depending on the automata rules. The car moves until it reaches a new cell and then the cycle of operations is repeated.
4. LOGIC GATES WITH CUBELETS
Previous to the development of CULET was some others models with similar capabilities. One of the most successful was a Cubelets-only car that were able to perform logic operations. CULET: Cubelets Lego Universal Turing Machine ECA Rule 110 [19] shows a video with some examples.
Figure 3 shows a photograph of this robot. The fundamental idea is the same that the one for CULET: a car that moves through a tape of cell and that is able to read and write in it. Here the tape is made of cubes: each cell is formed by a sensor distance and a flashlight; each time that the sensor detects a movement, the state of the flashlight (on or off) swaps. The car uses a rotator block to position the brightness sensor on top of the tape; the read operation is performed by moving the sensor on top of a flashlight; the write operation is done by moving the sensor on top of a distance sensor of the tape. The main inconveniences of this model are the following. First is the issue of the price: the bigger the program, the bigger the tape; CULET uses cheaper cell components than the logic gates machine. Second is the point of the coordination and calibration of the components: this model depends on delays for make a movement along the tape and to move the brightness sensor.

Logic gates implemented with Cubelets.
5. FINAL REMARKS
We developed a robotic Turing machine named CULET, able to simulate any 2-symbols Turing machine. CULET is constructed with autonomous cube-robots Cubelets and Lego® bricks. A video showing the function of the Turing machine simulating Rule 110 with CULET is available in CULET: Cubelets Lego Universal Turing Machine ECA Rule 110 [19] and the duplicator Turing machine in CULET: Cubelets Lego Doubler Turing Machine [20]. The full code to reprogram Cubelets is available from Code developed for CULET [21]. In the future work, we will develop machines reading more than two states.
Authors Introduction
Ricardo Q. Figueroa
 Ricardo Q. Figueroa is a researcher at the Artificial Life Robotics Lab in the Superior School of Computer Sciences, National Polytechnic Institute, Mexico City, Mexico. His areas of interest are robotics, swarm robotics, artificial life, cryptography.
Ricardo Q. Figueroa is a researcher at the Artificial Life Robotics Lab in the Superior School of Computer Sciences, National Polytechnic Institute, Mexico City, Mexico. His areas of interest are robotics, swarm robotics, artificial life, cryptography.
Daniel A. Zamorano
 Daniel A. Zamorano is a researcher at the Artificial Life Robotics Lab in the Superior School of Computer Sciences, National Polytechnic Institute, Mexico City, Mexico. Currently, his areas or work are cellular automata, complex systems, system security and artificial intelligence.
Daniel A. Zamorano is a researcher at the Artificial Life Robotics Lab in the Superior School of Computer Sciences, National Polytechnic Institute, Mexico City, Mexico. Currently, his areas or work are cellular automata, complex systems, system security and artificial intelligence.
Genaro J. Martínez
 Genaro J. Martínez is a professor at the School of Computer Sciences, National Polytechnic Institute, Mexico City, Mexico and visiting fellow at the Unconventional Computing Centre, University of the West of England, Bristol, UK. His does research in cellular automata, unconventional computing, artificial life, complex systems, and swarm robotics.
Genaro J. Martínez is a professor at the School of Computer Sciences, National Polytechnic Institute, Mexico City, Mexico and visiting fellow at the Unconventional Computing Centre, University of the West of England, Bristol, UK. His does research in cellular automata, unconventional computing, artificial life, complex systems, and swarm robotics.
Andrew Adamatzky
 Andrew Adamatzky is a professor at the Department of Computer Science and Director of the Unconventional Computing Centre, University of the West of England, Bristol, UK. He does research in reaction-diffusion computing, cellular automata, massive parallel computation, collective intelligence, bionics, complexity, non-linear science, novel hardware.
Andrew Adamatzky is a professor at the Department of Computer Science and Director of the Unconventional Computing Centre, University of the West of England, Bristol, UK. He does research in reaction-diffusion computing, cellular automata, massive parallel computation, collective intelligence, bionics, complexity, non-linear science, novel hardware.
Footnotes
REFERENCES
Cite this article
TY - JOUR AU - Ricardo Quezada Figueroa AU - Daniel Ayala Zamorano AU - Genaro Juárez Martínez AU - Andrew Adamatzky PY - 2019 DA - 2019/03/30 TI - A Turing Machine Constructed with Cubelets Robots JO - Journal of Robotics, Networking and Artificial Life SP - 265 EP - 268 VL - 5 IS - 4 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.190220.013 DO - 10.2991/jrnal.k.190220.013 ID - Figueroa2019 ER -
