An Improved Nonstationary Fuzzy System Approach versus Type-2 Fuzzy System for the Lifting Motion Control with Human-in-the-Loop Simulation
- DOI
- 10.2991/ijcis.11.1.14How to use a DOI?
- Keywords
- Human lifting motion; Nonstationary fuzzy system; Human body modeling; Type-2 fuzzy sets; Human in the loop simulation
- Abstract
People working in the fields of robotics, animation, computer graphics and computer vision, and biomechanics, find it difficult to conduct human motion simulations, such as lifting, walking and running. This is because it is difficult to predict all of the motion strategies in a variety of situations. The human lifting motion is hard work; at the same time, lifting is the most demanded robotic motion. In this paper, a fuzzy integral based nonstationary fuzzy inference system is proposed to control a five-segment human model for the human lifting motion with human-in-the-loop simulation. This system was designed to reduce the computational complexity of nonstationary fuzzy systems. Hence, this paper contributes to the literature in two ways: as an improved nonstationary fuzzy system and as a human lifting motion simulation framework. A fuzzy integral algorithm between the fuzzification and defuzzification stages has been used to aggregate the inference outputs of the nonstationary fuzzy controller. The fuzzy integral algorithm uses fuzzy values obtained during the fuzzification stage as the attribute values and the fuzzy values obtained by a one-loop quantum particle swarm optimization algorithm as the importance values. The computational complexity in the nonstationary fuzzy systems and type-2 fuzzy systems can be reduced between 25 to 60 percent with the improved nonstationary fuzzy system. An experimental application of the human lifting motion was carried out to demonstrate the effectiveness of the proposed approach. The results illustrated that the proposed algorithm can achieve increased simplicity, improved effectiveness, good robustness, and a higher precision of computation.
- Copyright
- © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Human motion simulations aim to predict natural human motions during manual tasks. Walking, running, lifting, and jumping are the most common human movements in daily life [1]. Consequently, controlling, understanding and recognizing human movements are important tasks for people in the fields of robotics, computer vision, ergonomics, and biomechanics [2–8]. The human lifting motion is a complex human movement. As such, the control of this motion is an unstable and ill-posed system, and hence, the importance of human lifting motion prediction strategies are a popular topic in the literature [9–14]. A simulation model of general human and humanoid motions has been presented in the literature for dynamical modeling. It has been verified with two sports examples [9]. In [10], an experimental validation was given for controlling humanoid robots using human motion data. Menegaldo [11] described a biomechanical model and the optimal control approach of human posture, based on a consistent approximation theory. The control results from this study involved two simulations solved by sequential quadratic programming. [13] and [14] concentrated on the human lifting simulation. In these studies, a multi-objective optimization approach was proposed to predict dynamic lifting for the human lifting simulation using a three dimensional human model [13]. In [13], the simulation results illustrate that the proposed approach, with two objective functions as the dynamic effort and stability, is good, but less sensitive to the stability criterion. Qu [14] proposed a fuzzy control based human lifting motion simulation. Two-dimensional lifting motions were simulated using fuzzy rules. These rules provided some of the properties of a neural controller. The block diagram for this method is shown in Fig. 1(a). The five segment human model has five angle points (Fig 1(b)). The control of the angles during the lifting simulation are dependent on each other. Therefore, a fuzzy-neural controller for each angle has been used in the algorithm.
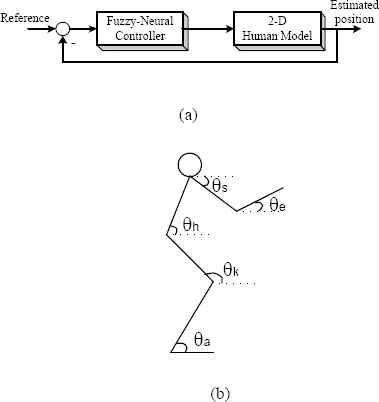
The selection and design of the controller used for a human lifting simulation are very important for acheiving a high level of accuracy. At this point, the application of fuzzy controllers is very useful. However, type-1 fuzzy systems are not enough and type-2 fuzzy systems require large computational times for the simulation of the human lifting motion. It is commonly known that type-1 fuzzy sets cannot directly handle uncertainties in the data, measurements, rule consequents and meanings of the words in the rules. That being said, type-2 fuzzy sets are very useful for modeling and minimizing the effect of uncertainties [15]. Fig. 2 illustrates fuzzy systems with a type-1 fuzzy set, type-2 fuzzy set and their membership degrees. Type-1 fuzzy sets have one argument that can be represented graphically with two dimensions. Type-2 fuzzy sets have two arguments that can be represented graphically with three dimensions. Therefore, type-2 fuzzy systems that use type-2 fuzzy sets in the antecedent and consequent parts are more complex than type-1 fuzzy systems. Despite the advantages obtained by type-2 fuzzy sets, an important problem is their high computational cost in practical applications [16–19].
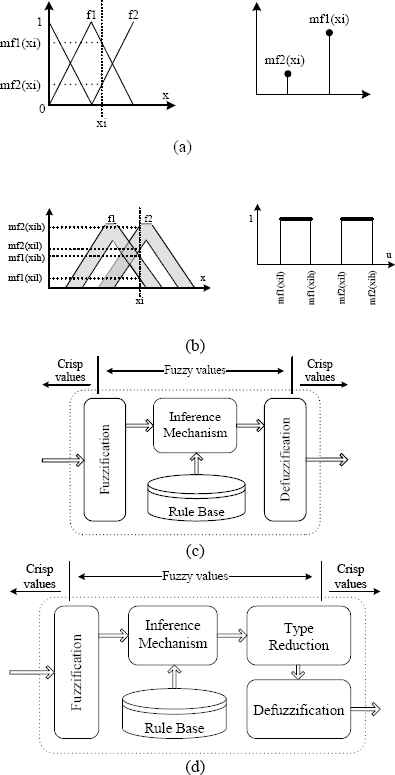
Degree of membership functions for: a) type-1 fuzzy set, b) type-2 fuzzy set, c) type-1 fuzzy system scheme, and d) type-2 fuzzy system scheme.
A number of attempts have been made to overcome the problem of the computational complexity of type-2 fuzzy systems [20–26]. Garibaldi [26] proposed nonstationary fuzzy sets and the concept of a perturbation function that is used for generating nonstationary fuzzy sets. A nonstationary fuzzy set is a collection set of type-1 fuzzy sets. It was obtained by repeatedly generating a membership function with some parameters.
The nonstationary fuzzy set is as follows [26]:
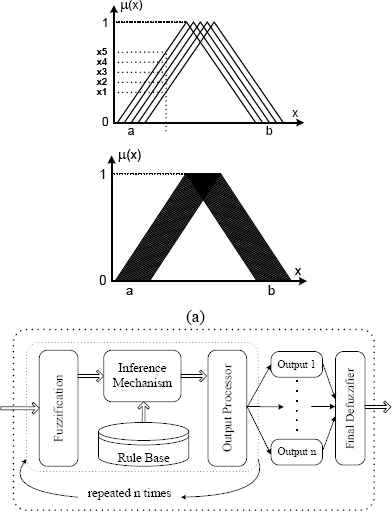
a) The nonstationary fuzzy sets obtained by the 5 and 25 type-1 triangular fuzzy sets, b) Schematic diagram of the nonstationary fuzzy inference system.
As shown in Fig. 3, the nonstationary inference system is a repeated type-1 inference system with different instantiations of the membership functions over time [26]. This approach is different from the type-2 fuzzy systems, as it does not have some of the difficulties of the type-2 fuzzy systems. However, the nonstationary fuzzy inference system still has computational costs resulting from the repetition of the type-1 fuzzy inference.
A novel approach that consists of an algorithm for improving the nonstationary fuzzy systems and a framework for the lifting motion control with human-in-the-loop simulation of humans is proposed in this study. The improved nonstationary fuzzy system is the first contribution in this paper. It is aimed as a fuzzy integral based algorithm used to reduce the computational complexity encountered by the nonstationary fuzzy inference systems. The human lifting simulation framework is the second contribution in this paper. This framework is aimed as a method to control fundamental human movements using a five segmented human model. It uses the first contribution to enable such systems to be used in practical applications. The experimental results illustrate the computational efficiency of the proposed nonstationary fuzzy system, comparisons with type-1, type-2, and nonstationary fuzzy control algorithms, and human lifting motion trajectories with real data that is a human.
In summary, the primary objective of this paper is to develop a human lifting motion simulation framework and an efficient strategy for the nonstationary fuzzy inference systems based on a fuzzy integral as shown in Fig. 4. The rest of this paper is organized as follows. Section 2 presents the structure of the improved nonstationary fuzzy system. Section 3 presents the experiments and results. Finally, Section 4 presents the conclusions and outcomes of this study.
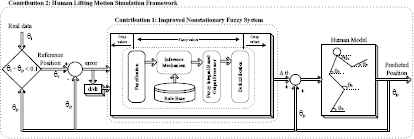
Block diagram of the proposed computational approach.
2. Improved Nonstationary Fuzzy System
2.1. Nonstationary Fuzzy Inference
The nonstationary fuzzy sets that model variability in type-1 fuzzy membership functions are obtained by repeatedly generating a type-1 membership function. A nonstationary fuzzy inference system is an iteration of membership functions using a perturbation function that does not affect the inference process [26]. Figure 5 is a graphical illustration of an example of the inference process using nonstationary triangle fuzzy sets that are instantiated only three times as uniform. As shown in Fig. 5, three values are obtained for each instantiation of a nonstationary fuzzy membership function. The minimum function is used for this example. This inference is done for each rule. The goal of the nonstationary fuzzy sets approach is to model uncertainties, such as type-2 fuzzy sets. Therefore, a nonstationary fuzzy set needs at least 30 more instantiations. However, the type of the nonstationary fuzzy sets may differ (e.g., triangular, Gaussian, or trapezoidal). In addition, the distributions of the instantiations in a nonstationary fuzzy set may be non-uniform. These factors increase the computational complexity of nonstationary fuzzy inference systems.
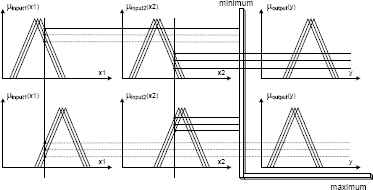
The Mamdani fuzzy inference process for nonstationary fuzzy membership functions.
A numerical example of a nonstationary fuzzy inference system with only three instantiations is shown in Fig. 6. The nonstationary fuzzy system given in Fig. 6 has two inputs (x1, x2) with two membership functions (A, B and C, D respectively) and one output (y) with three membership functions (E, F, G). The rule base consists of four rules as shown in Fig. 6(d). Fig. 6(a1–b1) illustrate the input membership functions. All of the nonstationary membership functions have three type-1 triangular fuzzy sets. Fig. 6(a2–b2) presents examples of the fuzzification values. In the fuzzification process, three fuzzy values for each nonstationary fuzzy set are obtained for the specific crisp input values. Thus, six fuzzy values for each input are calculated as illustrated in Fig. 6(a2–b2).
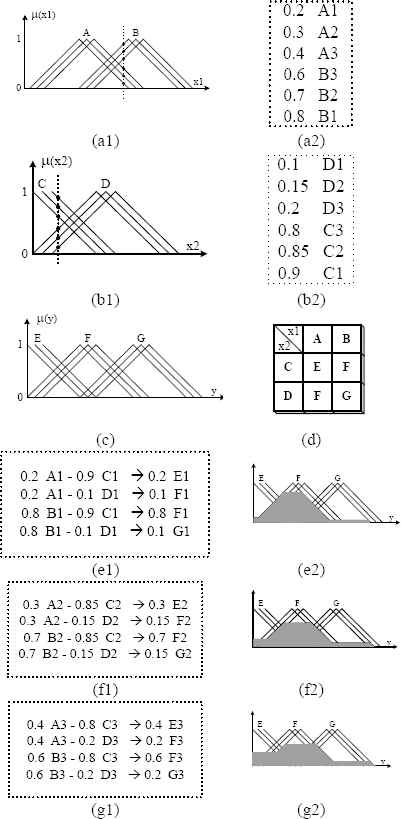
A numerical example for the nonstationary fuzzy inference with three instantiations. a1) Nonstationary fuzzy membership functions for first input, a2) Fuzzy values for first input, b1) Nonstationary fuzzy membership functions for second input, b2) Fuzzy values for second input, c) Nonstationary fuzzy membership functions for output, d) Rule table, e1-f1-g1) Inference results for first, second, and third instantiations, e2-f2-g2) Defuzzification for first, second, and third instantiations.
The terms A1, A2, and A3 are used for each instantiation of the input nonstationary fuzzy set A. The same naming convention has been used for other nonstationary fuzzy sets B, C, D, E, F and G. Fig. 6(e1-f1-g1) shows the inference mechanism for each instantiation using a minimum operator. As illustrated in Fig. 3, the nonstationary fuzzy systems have a repetitive type-1 fuzzy inference system with a number of instantiations of one nonstationary membership function. In this example, a nonstationary membership function has three type-1 fuzzy sets. Therefore, three type-1 fuzzy inference processes are conducted between the fuzzy sets with the same numbering. Fig. 6(e1) shows four implications as a conventional type-1 fuzzy inference mechanism. This nonstationary fuzzy inference system has 12 implications in total.
Finally, the representation of a defuzzification process is given in Fig. 6(e2-f2-g2). The results of this inference can be obtained with the defuzzification of all of the instantiations. As illustrated in Fig. 6, the inference process is performed for the number of instantiations to obtain the output fuzzy sets for each input value. Each output fuzzy set is used for the defuzzification to obtain the standard center of gravity.
2.2. Improved Nonstationary Fuzzy Inference
If a nonstationary fuzzy set needs more instantiations (e.g., 30, 100 or 1000), the computational cost of the inference system increases proportionally to the number of instantiations. In this study, a new approach is proposed to overcome this difficulty. Fig. 7 shows the schematic diagram of the proposed fuzzy integral based nonstationary fuzzy inference system.
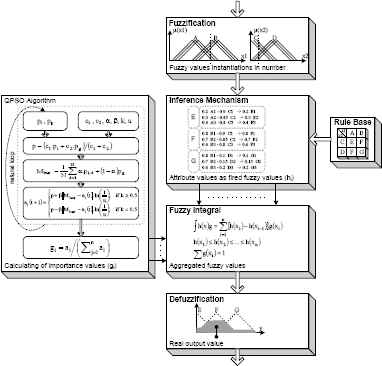
Overall description of the proposed approach.
Fuzzification Stage
The fuzzification interface transforms the input crisp values into a set of fuzzy values in the chosen number of instantiations. The membership function defined by Eq. (2) can be used for fuzzification [26]. Examples of the perturbation function, f(t), are sinus and rand. Figure 8 illustrates the membership functions and fuzzy sets for the type-1, type-2 and nonstationary fuzzy systems.
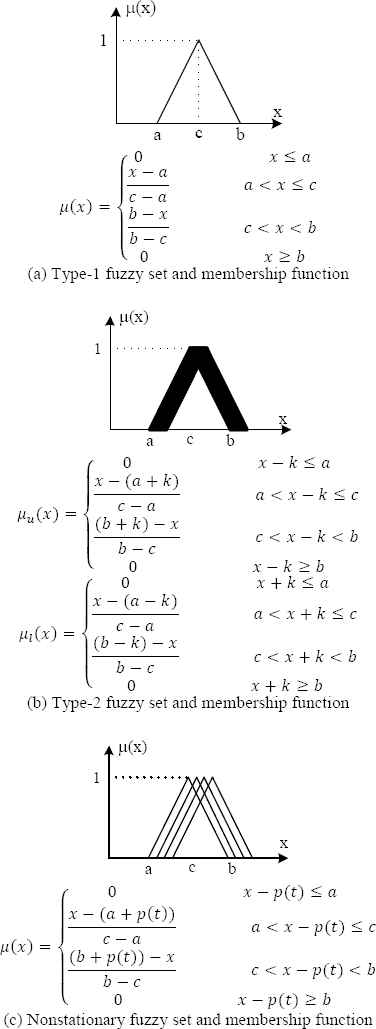
Membership functions for the type-1, type-2 and nonstationary fuzzy sets.
Rule Base
The rule base in the proposed approach is the same as that used for the conventional type-1 fuzzy logic systems.
Inference Mechanism Stage
The inference mechanism calculates the firing strengths of the activated rules. This is achieved through a combination of instantiations in the nonstationary fuzzy sets using the minimum and maximum operators for the intersection and union, respectively. The end result of the inference mechanism stage is a series of fuzzified output values which function as attribute values in the fuzzy integral stage.
Fuzzy Integral Stage
In the inference mechanism stage, fuzzy values from a number of instantiations are obtained for each fired rule. These fuzzy values belonging to the same output fuzzy set are aggregated with a fuzzy integral based on a quantum particle swarm optimization algorithm. As is well known, fuzzy set operations are extensively used for information aggregation [27]. The fuzzy integral that is an aggregation function using fuzzy measures is expressed as a computational scheme to integrate all of the values from the individual subsets [28].
The Choquet fuzzy integral, one of many fusion operators, can be computed as follows [27]:
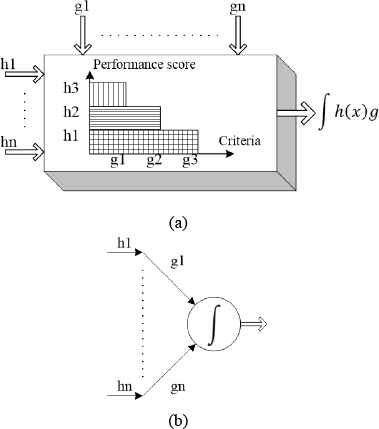
a) The structure of the Choquet fuzzy integral, b) The fusion of the fuzzy values in the nonstationary inference systems.
The attribute values (hi) for the Choquet fuzzy integral are the fuzzy values obtained by inferencing for each input configuration. The quantum particle swarm optimization (QPSO) is applied to extract the criteria (gi) related to the performance of each attribute value. To accomplish this, the effect values (ai) for each hi are calculated using the QPSO equations defined by Eq. (4)–(6) [28–29]. Finally, the gi values are obtained by Eq. (7):
Particle swarm optimization is a global search technique that illustrates advantages in speed and precision. In the classical particle swarm optimization, each particle in the space with position and velocity vectors represents a potential solution to the objective problem [29]. QPSO has a stronger search ability and quicker convergence speed. The state of a particle is defined by the quantum bit and angle [28–29]. The steps of the classical QPSO algorithm are as follows.
- Step 1.
Initialize the parameters and particles
- Step 2.
Evaluate the particle’s fitness
- Step 3.
Compare the particle to the personal and global best
- Step 4.
Update the Mbest and particle’s position
- Step 5.
Repeat the evolutionary cycle
These steps are the basis of the classical QPSO algorithm. More detail about the QPSO algorithm can be found in the reference section and the literature [28–29]. The second step does not need to work in this paper. However, the use of Steps 2 and 5 do improve the performance of the method. The mean squared error between the reference and the output of the system can be considered the fitness function. Although the QPSO algorithm continues between Step 2 and Step 5, until a good fitness or a maximum number of iterations is achieved, this algorithm is used for only one loop in this study. The values of the individual and best particle (pi and pg) are updated with new values at the end of this iteration. The other parameter values have also been generated during each iteration. A fuzzy system continuously evaluates new input values in any application. Therefore, a natural loop, as shown in Fig. 7, is created because the QPSO algorithm is used within our proposed fuzzy system. Thus, the performance of the fuzzy integral stage can be improved.
Table 1 and Fig. 10 illustrate the performance scores, effect values, criteria and fuzzy integral results for three examples. In Table 1, four cases for a nonstationary fuzzy set with three instantiations are given: hi as fuzzy values; ai as QPSO algorithm values; gi as importance values; and the results of the fuzzy integral stage are calculated for the example cases in the table. The fourth row in the table has been given as an example for the fuzzy values in Fig. 7. Fig. 10 shows the schematic representations of the Choquet fuzzy integral for the hi and gi values in Table 1. The coordinate axes consist of hi values in ascending order and the gi values that sum to 1.00 (Fig. 10(a–c)).
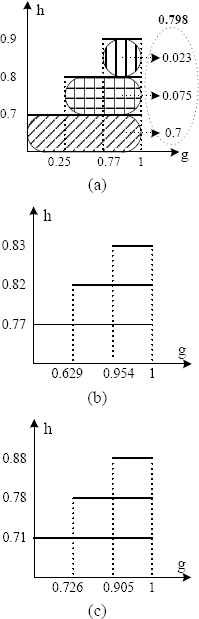
Aggregation of fuzzy values with a fuzzy integral.
| Exmp | hi | ai | gi | Result |
|---|---|---|---|---|
| 1 | 0.9 | 0.25 | 0.23 | |
| 0.8 | 0.57 | 0.52 | 0.798 | |
| 0.7 | 0.28 | 0.25 | ||
| 2 | 0.83 | 0.07 | 0.046 | |
| 0.82 | 0.52 | 0.325 | 0.789 | |
| 0.77 | 1 | 0.629 | ||
| 3 | 0.88 | 0.086 | 0.095 | |
| 0.78 | 0.162 | 0.179 | 0.740 | |
| 0.71 | 0.656 | 0.726 | ||
| 4 | E1 0.2 | 0.11 | 0.09 | |
| E2 0.3 | 0.74 | 0.61 | ||
| E3 0.4 | 0.37 | 0.30 | 0.321 E | |
| F1 0.8 | 0.04 | 0.02 | ||
| F2 0.7 | 0.66 | 0.42 | 0.754 F | |
| F3 0.6 | 0.91 | 0.56 | ||
| G1 0.1 | 0.41 | 0.56 | 0.162 G | |
| G2 0.35 | 0.23 | 0.32 | ||
| G3 0.2 | 0.09 | 0.12 | ||
Example results for the criteria and fuzzy integral
Defuzzification Stage
The last step in the proposed approach is turning the fuzzy variables generated by the fuzzy integral into a real value again.
Basically, nonstationary fuzzy sets consist of structures that are composed of multiple type-1 fuzzy sets that are homogeneously or heterogeneously distributed. Hence, when only one fuzzy value is obtained for a type-1 fuzzy set, a lot of fuzzy values are obtained to model the uncertainty region around the type-1 fuzzy set in nonstationary fuzzy sets. When this fuzzy set is used in a fuzzy system, each fuzzy value is processed and the algorithm needed to participate in the system is improved to obtain a more sensitive and robust system against the uncertainties. Conventional nonstationary fuzzy systems are processed by processing with nonstationary fuzzy sets in order and the output value is obtained by taking approximate averages. In the proposed method, the fuzzy values obtained from the type-1 fuzzy sets in the nonstationary fuzzy set are assigned optimal weight values or importance levels to each of them, and the inference mechanism according to these weights is realized. Thus, the system is both more efficient and faster. The reason why the proposed method is more efficient than the known nonstationary fuzzy systems is that the evaluation of each fuzzy value corresponding to the entry in the used system according to the importance grades can be made faster by optimizing these importance grades and by improving the speed of the general system. On the other hand, in addition to these advantages, in particular, if the uncertainty zones are known or predicted, thereby increasing the system efficiency by adjusting the significance levels in these regions by means of the proposed method. In the literature, with some studies including optimizing the use of type-2 fuzzy sets, these studies predict to apply the fuzzy system in its entirety or the entire fuzzy system in the same way. However, with this proposed method, the effect level of each slice of the fuzzy set can be adjusted. Moreover, this effect ratio is made by reducing the computational complexity by establishing a natural optimization cycle for each cycle. Hence, the proposed method aims to increase the performance of the system from different ways, except for the argument of computational complexity.
3. Experimental Results
The proposed fuzzy integral based nonstationary inference system was investigated by means of simulations in the MATLAB/Simulink. To analyze the behavior of the proposed approach, a human lifting simulation problem was considered; it was compared with the type-1, type-2 and nonstationary fuzzy systems.
The fuzzy logic systems (type-1, type-2, nonstationary, and proposed approach) were used as a controller. The same conditions were applied to obtain comparative results for all of the controllers. All fuzzy controllers were designed using the min-max implication and a center of gravity defuzzification method. The proposed approach using nonstationary type-1 and type-2 fuzzy controllers in all of the simulations consisted of two input variables and one output variable. Fig. 11 provides the rule table and membership functions of these fuzzy controllers. The universe of discourse to define the membership functions in all of the fuzzy controllers was divided into five domains for each input and seven domains for the outputs. Five instantiations with a homogeneous distribution were used in the proposed approach and the nonstationary fuzzy controller.
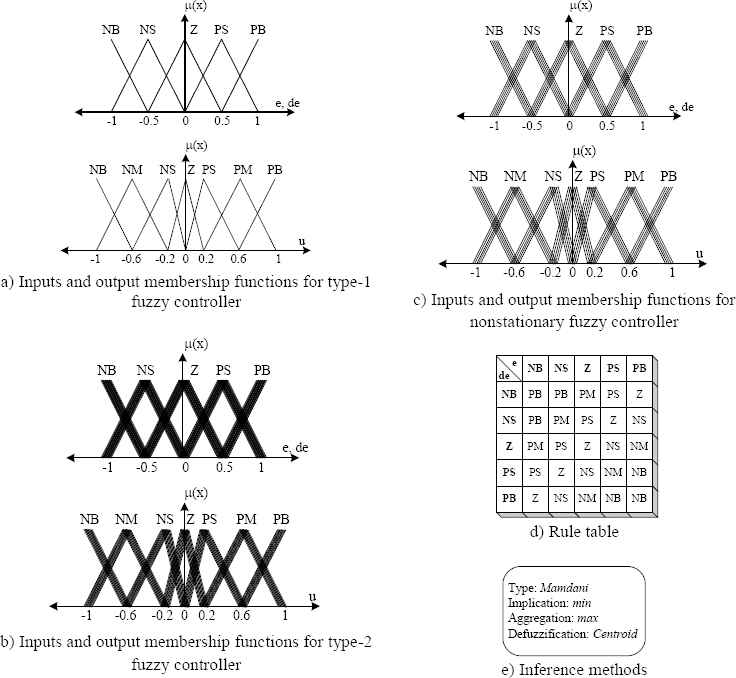
Membership functions and rule table for the fuzzy controllers. (NB: Negative Big, NS: Negative Small, Z: Zero, PS: Positive Small, PB: Positive Big.)
The computational complexity of the fuzzy controllers used in this study is shown in Table 2. The computational time of the proposed approach is much lower than that of nonstationary fuzzy systems and type-2 fuzzy systems. The fuzzy controllers were run on the same computer with a P4 3.0 GHz computer with 1.5 GB of RAM. All values were taken on the same conditions and were obtained for a fuzzy system with two inputs, one output, and 25 rules. Especially the increase of the number of inputs in the fuzzy system or the increase of the number of rules will increase the efficiency of the proposed method. Moreover, the proposed method is very suitable for real time realization and it can be successfully applied on today’s single board computer type embedded cards (Raspberry 3, Altera De0, …). Also, considering the speed and autonomous operation of today’s processors, it is seen that the computational times given in Table 2 are much lower.
| Controller Type | Computation Time |
|---|---|
| Type-1 FLC | 10 ms |
| Type-2 FLC | 35 ms |
| Nonstationary FLC | 30 ms |
| Improved Nonstationary FLC | 15 ms |
Computational time of the fuzzy controllers
The experimental application was chosen to simulate a human lifting motion with a fuzzy control. People working in the fields of robotics, animation, computer graphics and computer vision, and biomechanics, find it difficult to conduct human motion simulations, such as lifting, walking and running. This is because it is difficult to predict all of the motion strategies in a variety of situations. The human lifting motion is hard work; at the same time, lifting is the most demanded robotic motion. The human body can be represented as a five-segment model with angles for elbows, shoulders, hips, knees and ankles (θe, θs, θh, θk and θa, respectively), as illustrated in Fig. 12(a) [12, 14, 30]. Fig. 12(b) shows a computational model for the human body. Fig. 12(c) illustrates the geometric relationship between the human, the object and the shelf in a series of diagrams during the lifting duration.

a) Human model, b) Computational equations of human model, and c) human lifting motion phases.
Fig. 13 illustrates a control system model consisting of a fuzzy controller and a human body model. The human lifting motion aims to use hands to deliver an object to a target. The experiments were carried out to obtain comparisons between the proposed approach, nonstationary, type-1 and type-2 fuzzy controllers. Fig. 14 illustrates the normalized trajectories for each segment of the human body model, as angles of elbows, shoulders, hips, knees and ankles, for the predicted lifting motion with a medium target. As shown in Fig. 14, the proposed method is compared with the conventional nonstationary fuzzy system, type-1 fuzzy system, and type-2 fuzzy system. Given the comparative results for the five components of the human body, the proposed method seems to have a faster settling time, a smoother settling time and a lower error rate than the other fuzzy systems. As can be seen from the results, the proposed method is better not only in terms of speed but also in terms of control performance. The basic feature of the lifting motion is that it is a difficult control problem that contains different motion changes as mentioned before. It can be seen that the correctness and sensitivity of the proposed method is more robust than the other systems, while this motion with varying motion characteristics in Fig. 14 is different from angles of elbows, shoulders, hips, knees and ankles. The real and predicted lifting positions are shown in Fig. 15. The results have confirmed the effectiveness of the proposed approach, as compared to other controllers.
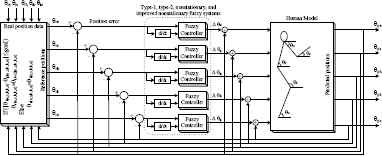
Block diagram of fuzzy control system for human lifting motion.
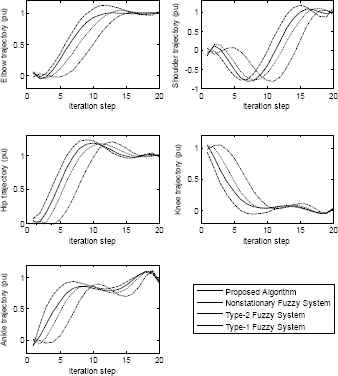
Predicted trajectories for the human lifting motion.
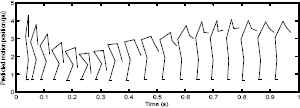
Real and predicted lifting motion frames.
4. Conclusions
The dynamic human lifting simulation is extremely popular in robotics, ergonomics, biomechanics, vision, and pathology analyses. This paper presented a new framework based on the improved nonstationary fuzzy for simulating the human lifting motion. An improved nonstationary fuzzy system is used for the proposed approach. Though type-1 fuzzy sets are characterized by the membership functions of one argument-two dimensions, type-2 fuzzy sets are characterized by the membership functions of two arguments-three dimensions. The nonstationary fuzzy sets that embed a type-2 fuzzy set to type-1 fuzzy sets include a collection of type-1 fuzzy sets, where each of the instantiations is derived from a perturbation function.
In this paper, the instantiations in a nonstationary fuzzy set are aggregated with a fuzzy integral using a quantum particle swarm optimization algorithm. This is the first contribution of this paper to the literature. Thus, the loop in the nonstationary fuzzy inference system is removed and a simpler and more effective algorithm is obtained. The prediction of the human lifting motion, as the second contribution to the literature, has been used for the experimental studies. The results have illustrated that the proposed algorithm has achieved a shorter computational time, more effective control action, better performance, smoother trajectories, and a more robust operation than the classical nonstationary fuzzy systems. More specifically, the improved nonstationary fuzzy system reduced the computational time by approximately 60 percent.
References
Cite this article
TY - JOUR AU - Mehmet Karakose PY - 2018 DA - 2018/01/01 TI - An Improved Nonstationary Fuzzy System Approach versus Type-2 Fuzzy System for the Lifting Motion Control with Human-in-the-Loop Simulation JO - International Journal of Computational Intelligence Systems SP - 183 EP - 194 VL - 11 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.11.1.14 DO - 10.2991/ijcis.11.1.14 ID - Karakose2018 ER -
