International Journal of Computational Intelligence Systems

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 9, Issue 4, August 2016, Pages 612 - 626

An Interpretable Logical Theory: The case of Compensatory Fuzzy Logic

Authors
Rafael A. Espin-Andrade
Universidad Autónoma de Coahuila, Blvd Revolución y Donato Guerra, s/n
Erick Gonzalez
Mathematical Center for Technical Sciences, Higher Technical University of Havana, 27 Calle 114 # 11901 e/ Ciclovía y Rotonda, Marianao, Havana, Cuba
Witold Pedrycz
Department of Electrical and Computer Engineering, University of Alberta, AB T6R 2G7, Edmonton, Canada
Eduardo Fernandez
Autonomous University of Sinaloa, Calzada de las Americas y Boulevard Universitarios s/n, Culiacán Rosales, Sinaloa 80040, Mexico
Received 5 August 2015, Accepted 20 February 2016, Available Online 1 August 2016.
DOI
10.1080/18756891.2016.1204111How to use a DOI?
Keywords
Interpretability; Compensatory Fuzzy Logic
Abstract

This paper aims to formally define a concept of interpretability according to natural language of a logical theory, and show advances for demonstrating that the logic system called Compensatory Fuzzy Logic is interpretable. A logical theory is interpretable according to natural language if the calculus based upon the elements of this logical theory can be understood in natural language and vice versa. We present conditions necessary for a logical theory to be called interpretable, especially Compensatory Fuzzy Logic.

Copyright
© 2016. the authors. Co-published by Atlantis Press and Taylor & Francis
Open Access
This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).

1. Introduction

Multidisciplinary sciences are the studies regarding an object of a known discipline, using variables, concepts, results, and methods of different disciplines. Interdisciplinary Sciences are studies regarding a new object not belonging to a specific discipline, using variables, concepts, results, and methods stemming from different disciplines.

However, our vocation is transdisciplinarian, which can be defined as studies creating theories and applications of them, combining variables, concepts, results and methods of different disciplines, into new variables, concepts, results and methods of a new theory (a transdiscipline).

Soft computing plays a role legate for transdisciplinarity, because its essential properties: (1) It realizes an open and multicultural space, (2) Includes evolutionary and Bio-inspired algorithms and (3) Allows hybridization.

Therefore, if Soft Computing inspires for the definition of transdisciplinary methods, then the following two characteristics can be articulated: General hybridization and theoretical hybridization are formally and experimentally justified by transdisciplinary logical theories. This definition of transdisciplinary methods leads to study many disciplines in another manner of understanding them.

For instance, a transdisciplinarian way to define and understand Knowledge Discovery, including the narrow sense of Knowledge Discovery, Knowledge Engineering and Decision Analysis, based on General and Theoretical Hybridization has to fulfill the following properties: Discovery of knowledge from all possible sources (human and factual ones) and their combination. Emphasis on Data Mining compound problems. Emphasis on knowledge based Decision Analysis, according preference knowledge, and knowledge regarding the relation between attributes and other variables of the problem.

The advantages of Knowledge Discovery with Fuzzy Predicates can be outlined as follows:

  • Generality: Their structures could deal with a wide spectrum of Data Mining problems (Clusters, Association Rules, Classification Rules, etc.) and Decision Making Analysis and Support problems as well.

  • Language Interpretability possibilities

  • Graphical Interpretability: Trees, graphs, neural networks, maps, other ones

The possibilities of communication can be based on clear mapping among semiotic registers, Natural or professional language, Fuzzy Logic Predicates, Trees, Neural Networks or Graphs, Cognitive Maps and Informatics Language (For example Fuzzy Description Logics).

This paper aims to introduce a formal definition of interpretability, which is the property fulfilled by a logical theory, such that there is a two sided relation between the results of the calculus upon the field of such theory over its objects by using its operators, and on the other side, the meanings of them represented in the natural or professional language. The interchange between the field of the logical theory calculus and the natural or professional language representation should be transparent, but not necessarily isomorphic, with the purpose to represent the knowledge.

This definition needs to be a transdisciplinary one by taking into account important elements of different mathematical disciplines. This paper proposes a way to advance towards Knowledge Engineering intention of modelling tacit knowledge into explicit formal models using a logical theory.

This is simultaneously a way to construct a transdisciplinary logical theory, looking for the proposed definition of Interpretability. Epigraph 2 introduces the new transdisciplinary way to understand interpretability and epigraph 3 introduces in this context the principal elements of a logical theory called Compensatory Fuzzy Logic. Sections 4 and 5, explain and illustrate propositions in relation with decision making, bivalent logic and statistics. Finally, sections 6, 7 and 8 resume advances, conclusions and outline future research. Interpretability of a logical theory

The previous attempts to achieve interpretability by means of fuzzy logic and fuzzy sets can be found in many well-known approaches like fuzzy control (Fuzzy Systems), fuzzy operators, t-norms and t-conorms and Computing with Words (CWW) among others.

However, Fuzzy Control is limited to rules and is not compatible with classical rationality and the evolution considered towards more accurate methods affects the interpretability1,2, the isolated operators are limited to deal with interpretability by labels.3–6

The t-norm and t-conorm approach and Fuzzy Logic, in general, offers a formal treatment, but without practical results according interpretability and do not include the treatment of fuzzy systems by rules. 5–12 Computing with Words (CWW), Linguistic Data Summarization, use specific structures called protoforms and they are not recognized in the areas of, Natural Language Processing (NLP) and Natural Language understanding (NLU). 13–16

To sum up, the interpretability approaches by fuzzy logic and fuzzy sets exhibit at least one of the following deficiencies: (1) a lack of compatibility with classical rationality, (2) a lack of compatibility with human behavior, (3) a lack of consideration of Fuzzy Systems study or (4) a contradiction between interpretability and accuracy.

Two other theories define interpretability as an essential concept. Those are the Languages theory17 and the Models theory18, 19. As indicated by languages theory, a theory T is interpretable in (according) S, if the language of T can be translated to the language of S, in such a way, that theory S proves each theorem translation of T, see Ref. 20.

In Model theory, a structure A is said to interpret a structure B (viz. B interpretable in A) if there is a definable subset D of A, and definable relations and functions on D, such that B is isomorphic to the structure with domain D and these functions and relations.

This allows representing elements of B using elements of D, operate with this representation, using operations of structure A and return the results to the structure B, see Ref. 19.

Our point of view to resolve the scientific problem explained above is that interpretability of a logical theory according language, should be Interpretability according logical theories and paradigms associated with social practices very much in relation with natural and professional language like and Logics, Decision Making theories and methods, Mathematical Statistics and others.

Hence, the hypothesis that we prove on this paper is the following: a theoretical approach of interpretable theories by Bivalent Logic, and compatible with selected elements of Decision Making theories and Mathematical Statistics will be compatible with human behavior, Knowledge Discovery methods for particular problems, Mamdani approach for Fuzzy Systems and accuracy improvement of its application in complex and/or high dimensionality problems of fuzzy control. The points that we should follow to demonstrate that a logical theory is interpretable are stated below:

  1. 1.

    Creating a new theoretical approach interpretable by Bivalent Logic, and compatible with selected elements of Decision Making theories and Mathematical Statistics

  2. 2.

    Elaboration on computational tools

  3. 3.

    Applications to different fields

  4. 4.

    Elaboration and application of experiments testing the following elements:

    • 4.1.

      Compatibility with human behavior,

    • 4.2.

      Compatibility with Knowledge Discovery methods for particular problems

    • 4.3.

      Compatibility with the Mamdani approach in simple cases,

    • 4.4.

      Accuracy improvement in complex and high dimensional cases of Fuzzy Control,

    • 4.5.

      Compatibility with protoforms used in CWW and LDS

    • 4.6.

      Robustness.

This study demonstrates that Compensatory Fuzzy Logic is a logical theory, which satisfies the first point specified above. 21–23

So far, we have proved that this fuzzy logic system can be defined as interpretable, according to our definition of interpretability. We introduce the notions of Compensatory Fuzzy Logic.

2. Introduction to Compensatory Fuzzy Logic

Compensatory Fuzzy Logic (CFL) is a multivalued logic axiomatic approach different of norm and conorm axiomatic. They must satisfy characteristics of descriptive approach of decision-making and the normative approaches to decision making. 21–23

It is based on four operators (denoted as c,d,n,o).

Here: c: [0,1]n → [0,1] is called conjunction, d: [0,1]n → [0,1] disjunction, n: [0,1] → [0,1] negation and o: [0,1]2 → [0,1] fuzzy-strict ordering.

It satisfies the following axioms listed below:

  1. (i)

    Compensation Axiom

    • min(x1,x2,…,xn)≤c(x1,x2,…,xn)≤max(x1,x2,…,xn)

  2. (ii)

    Symmetry or Commutativity Axiom

    • c(x1,x2,…,xi,…,xj,…,xn)=c(x1,x2,…,xj,,…,xi,…,xn)

  3. (iii)

    Strict Growth Axiom

    If x1=y1, x2=y2, …., xi-1=yi-1, xi+1=yi+1,…., xn=yn are different to zero and xi>yi then c(x1,x2,…,xn)>c(y1,y2,…,yn)

  4. (iv)

    Veto Axiom If xi=0 for any i then c(x)=0.

  5. (v)

    Fuzzy Reciprocity Axiom o(x,y) = n[o(y,x)].

  6. (vi)

    Fuzzy Transitivity Axiom If o(x,y) ≥ 0.5 and o(y,z) ≥ 0.5, then o(x, z)≥max(o(x,y),o(y,z))

  7. (vii)

    De Morgan’s Laws:

    n(c(x1,x2,…,xn)) = d(n(x1),n(x2),…,n(xn)) n(d(x1,x2,…,xn)) = c(n(x1),n(x2),…,n(xn))

Implications can be defined in different ways:

  1. 1.

    S-implication: S(x,y)=d(n(x),y), where d and n are the disjunction and negation operators, respectively.

  2. 2.

    R-implication: R(x,y)=sup{z∈[0,1]:c(x,z)≤y}, where c is the conjunction operator.

  3. 3.

    QL-implication, IQL(x,y)=d(n(x),c(x,y))

  4. 4.

    A-implication: The operator satisfies a group of axioms, which implicitly associate it with the conjunction, disjunction and negation operators

    For example, the Law of Importation (xΛy→z)↔(x→(y→z)) is one of its axioms, where the symbol ↔ is the logic equivalence.

The quasi-arithmetic means, which include for example the geometric mean, are operators expressed in the following form

Mf(x1,x2,…,xn)=f−1(1n∑i=1nf(xi))
where f is a strictly monotone continuous function which is extended to non-defined points by using the corresponding limit. These operators satisfy axioms i-iii. If, in addition, we have that for all i∈{1,2,…,n}limxi→0Mf(x1,x2,…,xn)=0 axiom (iv) is satisfied as well.
d(x1,x2,…,xn)=1−f−1(1n∑i=1nf(1−xi))
n(x)=1−x
and
o(x,y)=0.5[x−y]+0.5

We have a family of CFLs called Quasi Arithmetic Mean based Compensatory Logic (QAMBCL).

The function

U:X→[0,1],x=(x1,x2,…,xn)∈XU(x)=∀i∈{1,2,…,n}i p(xi)=∧i∈{1,2,…,n}p(xi)=f−1(1n∑i=1nf(p(xi)))
is the universal proposition.

And the function

E:X→[0,1],x=(x1,x2,…,xn)∈XE(x)=∃i∈{1,2,…,n}i p(xi)=∨i∈{1,2,…,n}p(xi)=1−f−1(1n∑i=1nf(1−p(xi)))
is the existential proposition.

For continuous cases, the formulas of universal and existential propositions are expressed as follows.

∀x∈Xp(x)={f−1(∫xf(p(x))dx∫xdx)if p(x)>0  for all x∈X0               In any other case
∃x∈Xp(x)={1- f−1(∫xf(1-p(x))dx∫xdx)if p(x)>0  for all x∈X0               In any other case

Furthermore particular system of QAMBCL is the Geometric Mean based Compensatory Logic (GMBCL), where conjunction and disjunction operators are expressed in the following manner

c(x1,x2,….,xn)=(x1.x2…..xn)1/n=exp(1n∑i=1nln(xi))

Negation is n(x) = 1-x and disjunction is the dual of the conjunction, namely

d(x1,x2,….,xn)=1−((1−x1)(1−x2)….(1−xn))1/n=1−exp(1n∑i=1nln(1−xi))

Refer to the series of figures, Fig. 1 – 4.

Fig. 1.

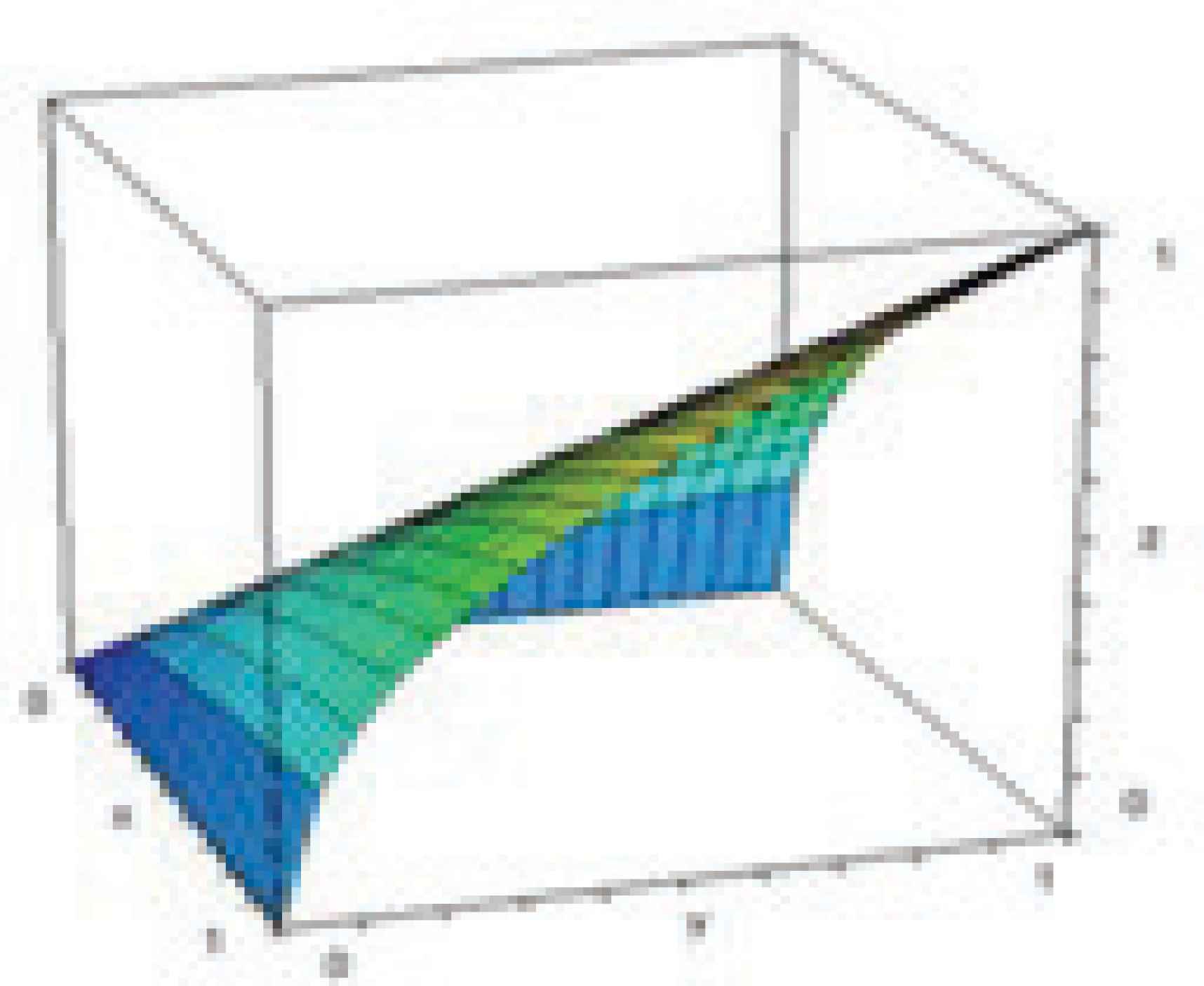
The conjunction operator in the form of the Geometric Mean.

Fig. 2.

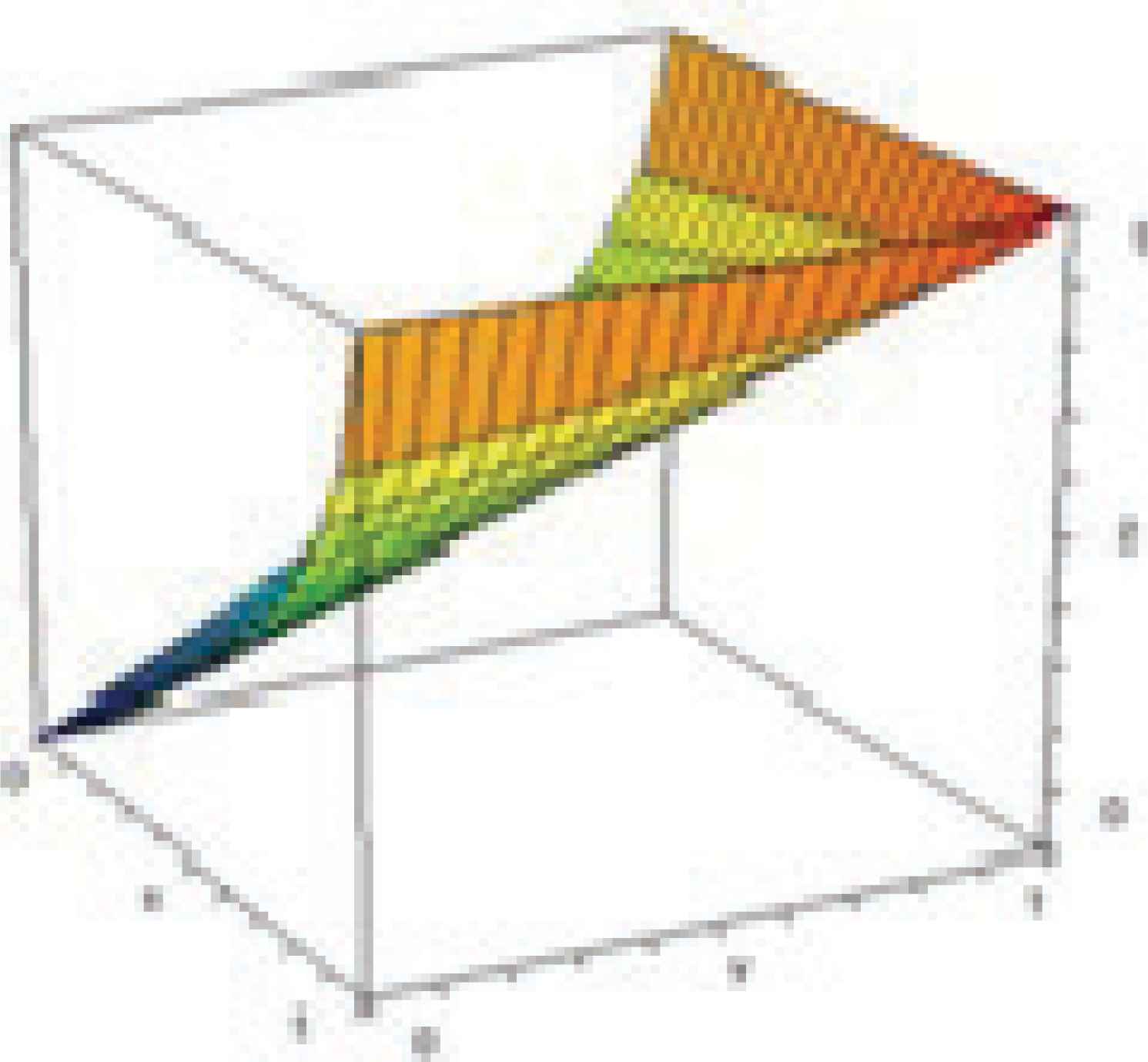
Disjunction operator as the dual of the Geometric Mean.

Fig. 3.

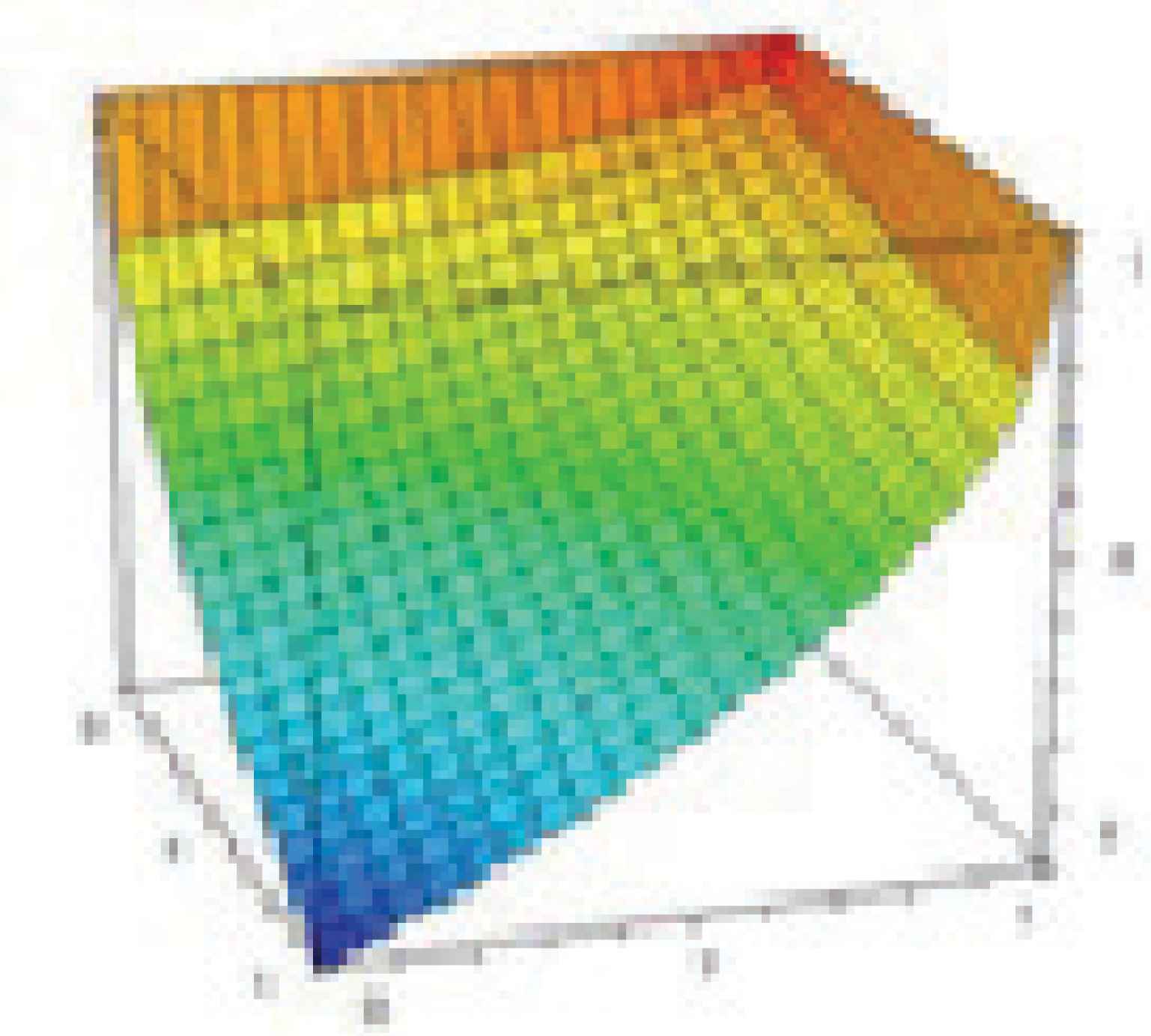
i(x,y)=d(n(x),y) S-implication defined for GMBCL

Fig. 4.

i(x,y)=d(n(x),c(x,y)) QL-implication defined for GMBCL

The universal and existential operators defined for the GMBCL are stated in the form (in case of discrete variables).

∀x∈Up(x)=∧x∈Up(x)=∏x∈Up(x)n={exp(∑x∈Uln(p(x)))n) for  x:p(x)≠0,                  0, in any other case
∃x∈Up(x)=∨x∈Up(x)=1−∏x∈U(1−p(x))n=={1−exp(1n∑x∈Uln(1−p(x))) for  x:p(x)≠1,               1                     in any other case

The continuous versions of these formulas read as follows

∀x p(x)={    ∫Xln(p(x))dx∫Xdxeif p(x)>0 for any x∈X0                 in any other case
∃x p(x)={               ∫Xln(1−p(x))dx∫Xdx      1−e      if p(x)<1 for any x∈X1                             in any other case

3. Interpretability of CFL in the setting of Decision Making theories

The axioms of CFL is compatible with many axioms of normative Decision Theory, while the compound predicates can be understood as utility functions.

CFL satisfies that conjunction and disjunction have the behavior of multiattribute value functions theory. These operators fulfill the strictly increasing property and also the De Morgan properties as very consensual properties, as well as the veto option, which is common for European School and multiplicative value theory.

In CFL conjunction and disjunction are not associative because of the convenience of differentiate among different attributes hierarchies like AHP and ANP are used to do, but even better differentiating conjunctive trees and disjunctive trees.24,25 Then, like all compensatory operators are not associative, it is enough to take compensatory operators satisfying veto and strictly growth as a way to satisfy the desired properties.

Conditionals can deal with properties like dependence between attributes, situation, which is not possible in the framework of Multiattribute value function theory.

Fuzzy predicates have the ability to deal with binary relations as well. They are adequate tools for modeling preferences between alternatives and attributes. Then, a fuzzy strict order relation is introduced in correspondence with the negation used into the De Morgan properties.

Example 1.

(Decision making illustrating interpretability in a Competitive Positioning Model, see Ref. 26.)

According to experts, an enterprise is competitive in a line of products in a market, if its economy is solid, its technological position is advanced and it is very strong in this product line in this market.

The attributes in the model are the following:

c(x):

Enterprise x is competitive.

s(x):

Enterprise x has a solid economy

T(x):

Enterprise x has an advanced technological position.

l(x):

Enterprise x is strong in the line of products in this market.

The predicate obtained for defining competitiveness is c(x)= s(x)∧T(x)∧l2(x). This example can be represented by the logical tree of the Fig. 5.

Fig. 5.

Logical tree representing the predicates considered in example 1.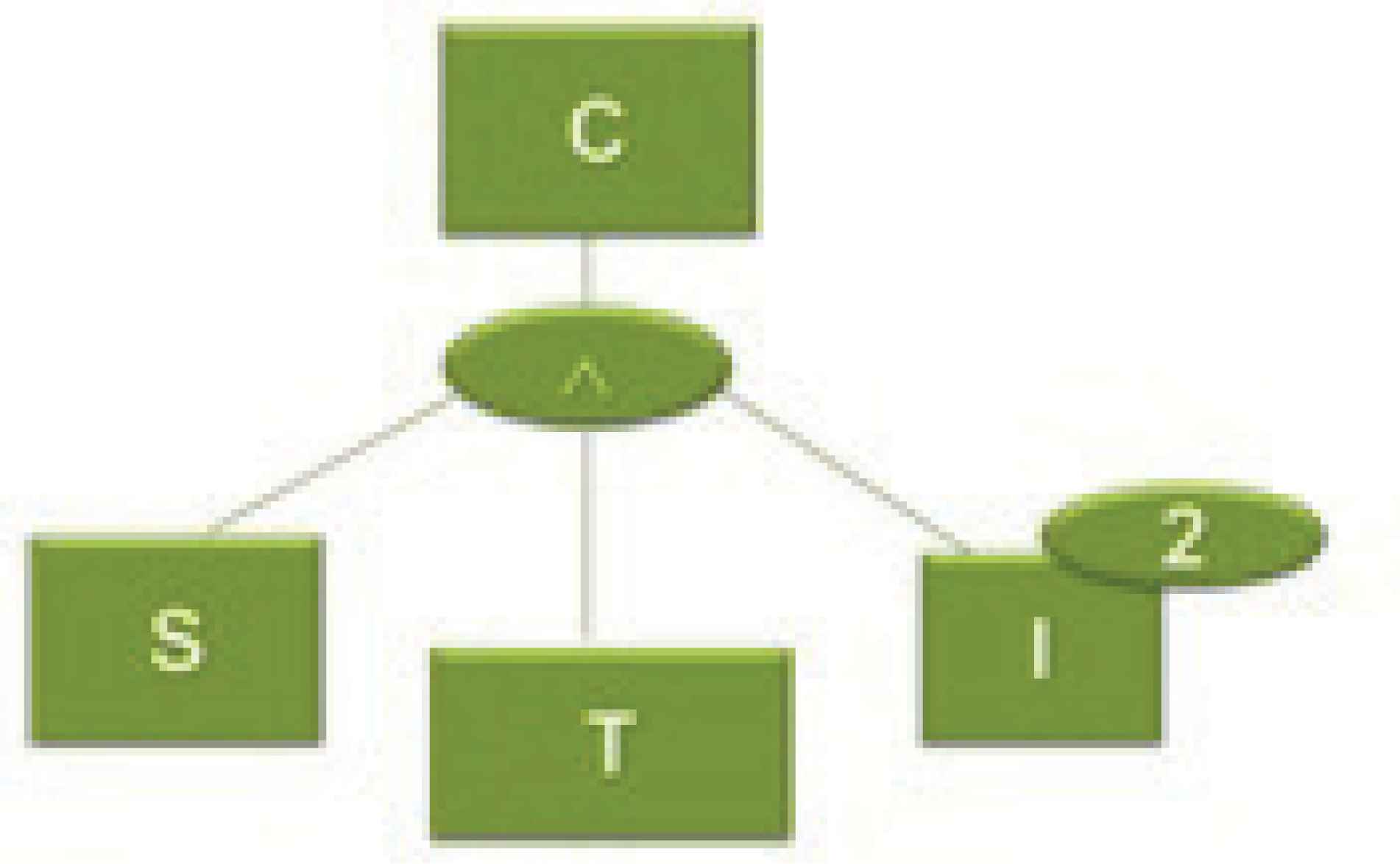

The attribute of solid economy can be stated as: An enterprise has a solid economy if it has a nice financial state and good amount of sales. Whether financial state would be somewhat negative, it should be compensated by a very good amount of sales.

Then, the initial model takes into account the more accurate predicate s(x)=(f(x)∧V(x))∧((¬f(x))0.5→V(x)2), where the new attributes are represented by the propositions:

s(x):

Enterprises x has a solid economy.

f(x):

Enterprises x has good financial state.

V(x):

Enterprises x has good amount of sales.

The new logic tree is shown in Fig. 6.

Fig. 6.

Developed logical tree resulting from Fig. 5.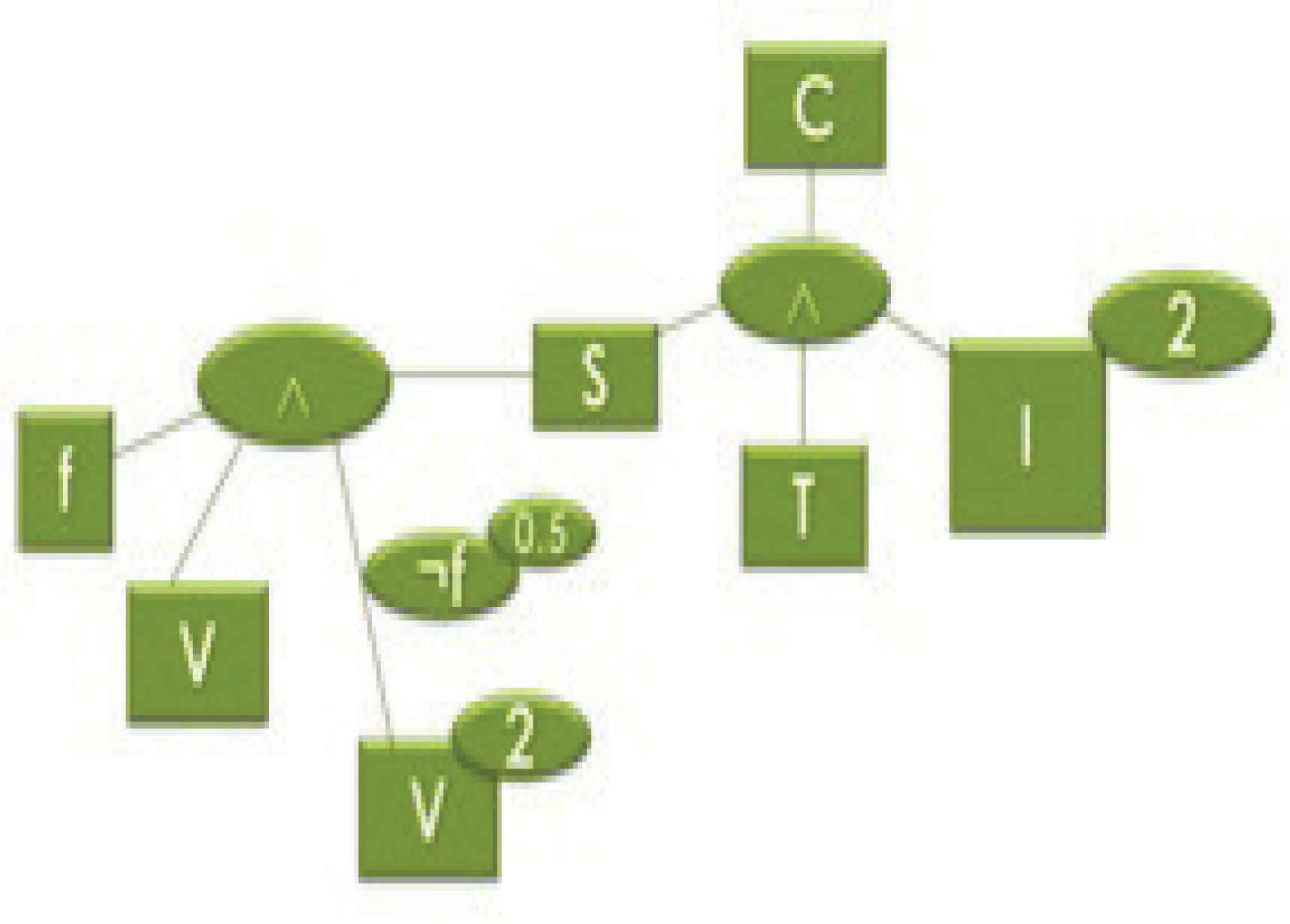

An even more accurate model introduces the concept of advanced technological position according to the following statement:

An Enterprise has an advanced technological position if its present technology is good; it owns patents, or many products in Research-Development Projects, or it is used to use important amount of money for Research Development Project. If its technology is not good, then it should have many products in Research-Development Projects or it is used to use very important amount of money for this kind of projects.

Now, the model includes the compound predicate

T(x)=t(x)∧(p(x)∨i(x)∨d(x))∧((¬t)0.5(x)→(p2(x)∨i2(x)∨d2(x)),
where:
T(x):

Enterprises x has an advanced technological position

t(x):

Enterprises x present technology is good

p(x):

Enterprises x owns patents

i(x):

Enterprises x has products in research-development projects

d(x):

Enterprises x is used to use important amount of money for research-development projects the resulting tree is represented in Fig. 7.
Fig. 7.

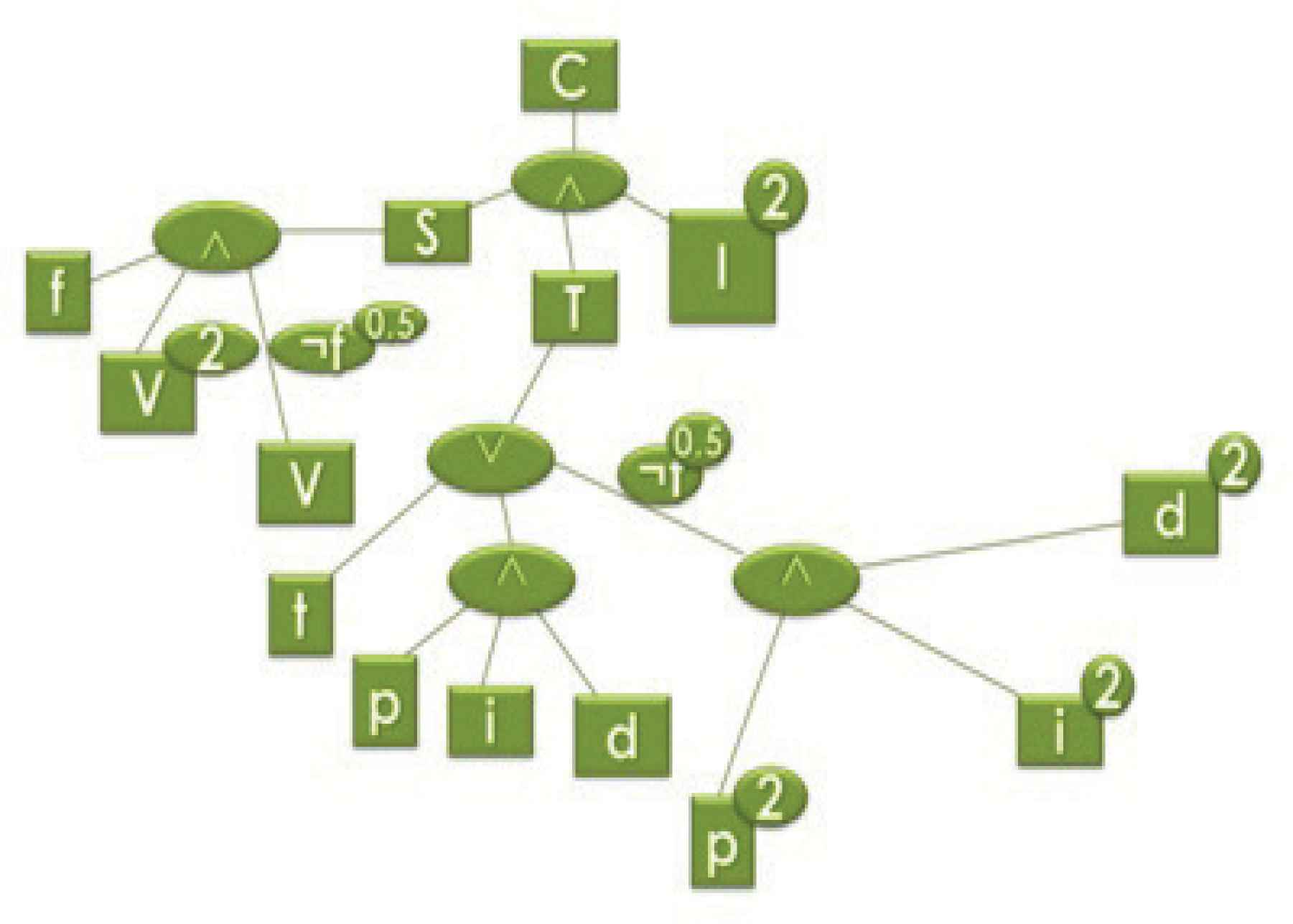
The logical tree of Fig. 6.

If the concept of good in a line of products in a market is defined like: An enterprise is good in a line of products in a market, if it has a strong position on that market, a diverse line of products, and it is independent of providers, then l(x)= m(x) ∧vl(x) ∧ip(x), where:

l(x):

x is good in the line of products

m(x):

x is strong in the market

vl(x):

x has a diverse line of products

ip(x):

x is independent of its providers

Then, the tree is represented in Fig. 8.

Fig. 8.

Final version of the logical tree representing example 1.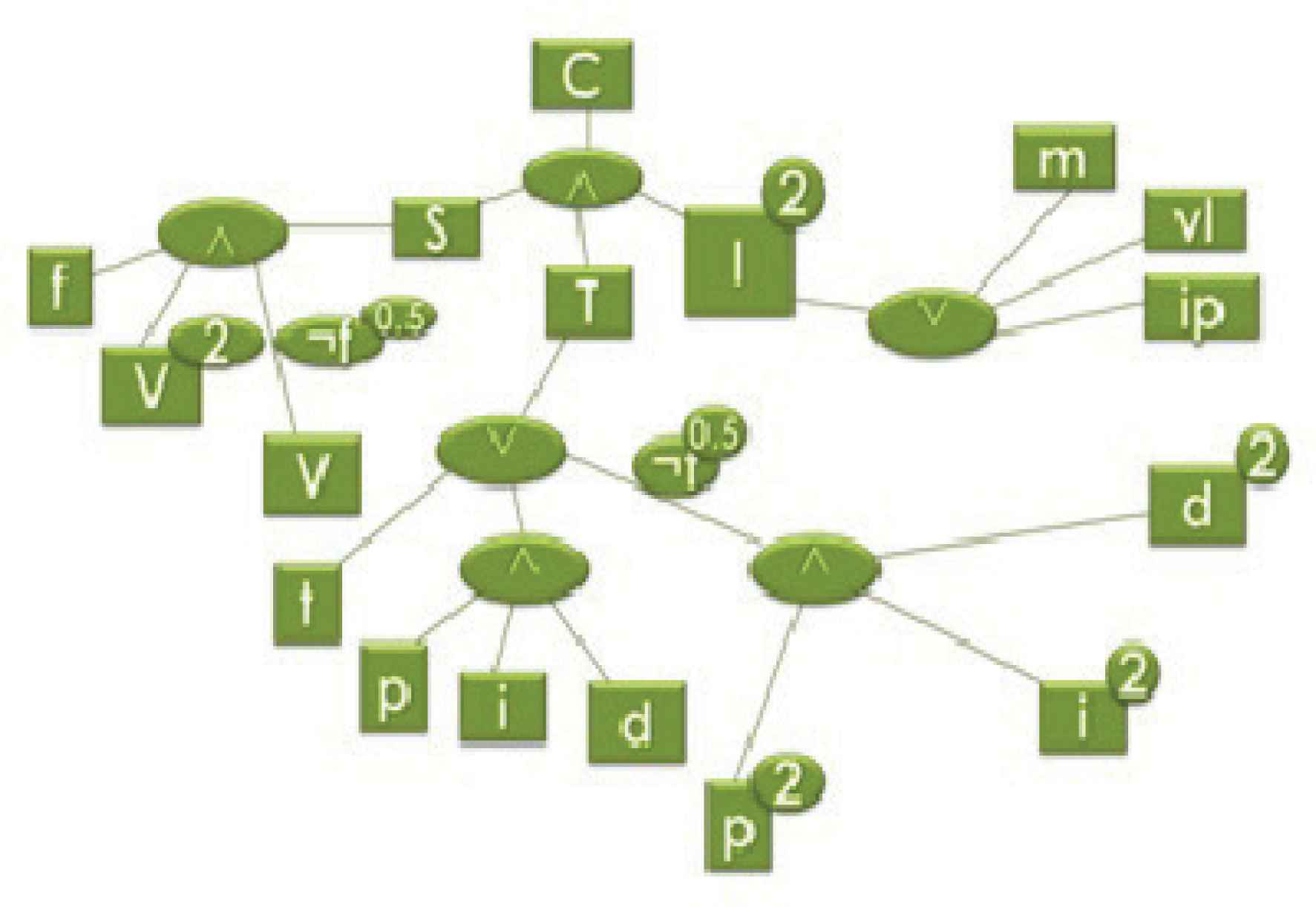

The model above was applied to study Tissue adhesive markets, particularly companies that we call A, B, C y D, and the results are summarized in tables 1 and 2. Table 1 shows the truth values of the basic predicates, obtained directly from expert or from data using the correspondent membership functions. Table 2 contains the truth values of mixed predicates calculated from the ones in table 1, using the predicates formulas. See ref 26.

x A B C D
f(x) 0.5 0.6 0.9 0
V(x) 0.47 0.63 0.75 0.99
t(x) 0.3 0.5 0.7 0.8
P(x) 0.93 0.41 0.62 0.81
i(x) 0.81 1 0.55 0.79
d(x) 0.61 0.95 0 0.7
Ip(x) 0.6 0.8 1 0.5
vl(x) 0.23 0.77 0.92 0.39
m(x) 0.1 0.4 0.8 1
Table 1.

Results of the model applied to the case study for tissue adhesive markets.

x A B C D
S(x) 0.5 0.611 0.812 0
T(x) 0.516 0.682 0.584 0.763
l(x) 0.234 0.627 0.903 0.58
L2(x) 0.058 0.393 0.815 0.336
C(x) 0.246 0.545 0.728 0
Table 2.

Final results of the model applied to the case study for tissue adhesive markets. Geometric mean based Compensatory Logic with the correspondent QL implication were used.

Taking into account the results shown in Tables 1 and 2, particularly the values appeared on the last line of table 2, we can conclude that company C is the most competitive, with truth value equals to 0.728.

Due to interpretability of CFL, this conclusion has a meaning according to natural language, we can use the phrase expressed in natural language: ‘competitiveness of company C is somewhat true’, see table 3.

Truth value Category
0 0 Aabsolutely false
0.1 Aalmost false
0.2 Eenough false
0.3 Ssomewhat false
0.4 mmore false than true
0.5 Aas true as false
0.6 mmore true than false
0.7 Ssomewhat true
0.8 Eenough true
0.9 Aalmost true
1 absolutely true
Table 3.

Categorical table of truth values

4. Interpretability of CFL according to Bivalent Logic and Statistics

CFL is interpretable according to bivalent logic in the sense that the continuity (or a finite number of removable discontinuities) of CFL operators allows to approximate the validity of a formula in CFL by the validity of that formula in the bivalent logic, if the neighborhood of truth values is enough small.

Bivalent logic offers a classical point of view of interpretability, where every predicate has been historically used as the manner to represent knowledge in formal sciences like mathematics or physics.

Definition 1.

(See Ref. 27)

A Compensatory Inference System is the combination of a Compensatory Logic and an implication operator.

In this context, an implication is a continuous operator (or at least with a finite number of removable discontinuities) i: [0,1]2→[0,1] which satisfy the truth table of the Bivalent Logic.

Definition 2.

Formulas of CFL Propositional Calculus are composed functions p:[0,1]n→[0,1] of the operators c, d, n and i.

Definition 3.

Let p(x) be a formula of the propositional calculus in CFL. A formula is valid according CFL if whatever could be Δ, 0<Δ<1, exist a set S of neighborhoods of elements belonging to {0,1}n such that the CFL universal proposition ∀x ∈S p(x) is greater than Δ.

Theorem 1.

Let ϕ be a formula of the propositional calculus, then ϕ is valid in the bivalent logic, if and only if, it is valid according CFL.

Theorem 1 demonstrates the interpretability of CFL according to bivalent logic.

Theorem 2.

If p(x)>0 for any x in a universe X, then the formula of the universal proposition ∀x∈Mp(x)=f−1(1n∑x∈Mf(p(x))) over any probabilistic sample M of S, of the predicate p(x), is a statistical estimator of the truth value of the universal proposition over X.

Theorem 2 proofs interpretability properties of CFL according to statistics. We have to take into account that probability theory is also a wide accepted and validated theory of mathematics applied to many social, natural and exact sciences.

The last result proves the possibilities for getting knowledge from samples and Monte Carlo simulations with the character of estimators over the universe.

Therefore, there are two kinds of Knowledge Discovery by predicates:

  1. 1.

    Searching is made using as objective function, the universal proposition truth value of a specific predicate over the set of instances of the used Data Base, changing the parameters values of the membership functions, adjusting them for improving the truth value of a hypothesis (Local search by optimization methods).

  2. 2.

    Modifying the structure of predicates, looking into the space of all possible predicates. (Global search by metaheuristics).

Example 2.

(Hypothesis of Mexican economy to illustrate the first kind of Knowledge Discovery).

There are three dynamical hypotheses for describing the Mexican economy in natural language:

  1. 1.

    If past time t from t0 is short, GDP at t0 is high, and exchange rate peso-dollar is good and inflation too, then inflation at t0+t will be good. (sufficient condition for goodness of future inflation).

  2. 2.

    If past time t from t0 is short, GDP at t0 is high, and exchange rate peso-dollar is good, and inflation too, then exchange rate at t0+t will be good. (sufficient condition for goodness of future exchange rate)

  3. 3.

    If past time t from t0 is short, GDP at t0 is high, and exchange rate peso-dollar is good, and inflation too, then GDP at t0+t will be high. (sufficient condition for goodness of future GDP)

We use Eq. (15) to calculate the parameters of the sigmoidal membership functions, see Eq. (16).

α=ln(0.9)−ln(0.1)γ−β
u(x)=11+e−α(x−γ)
where γ is the preimage of 0.5, which means ‘as true as false’ and β is the preimage of 0.1 or ‘almost absolutely false’, see table 3.

Figures 9 and 10 plot hypothetical sigmoidal membership functions for illustrating the influence of the meaning of the membership function when the parameters β and γ are changed.

Fig. 9:

Membership function of ‘As true as false’:10; ‘Almost absolutely false’:5.

Fig. 10:

‘As true as false’:40; ‘Almost absolutely false’:15.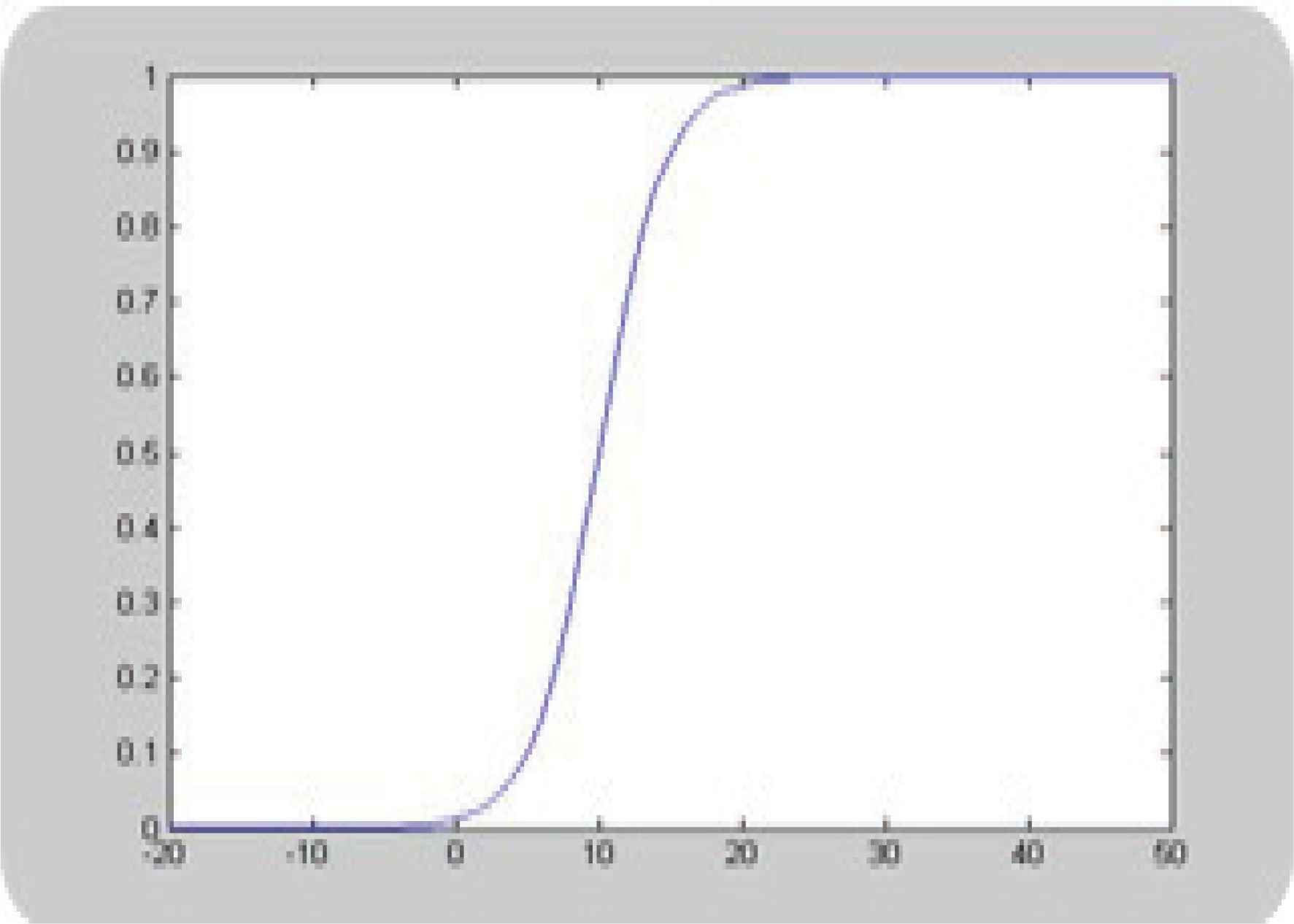

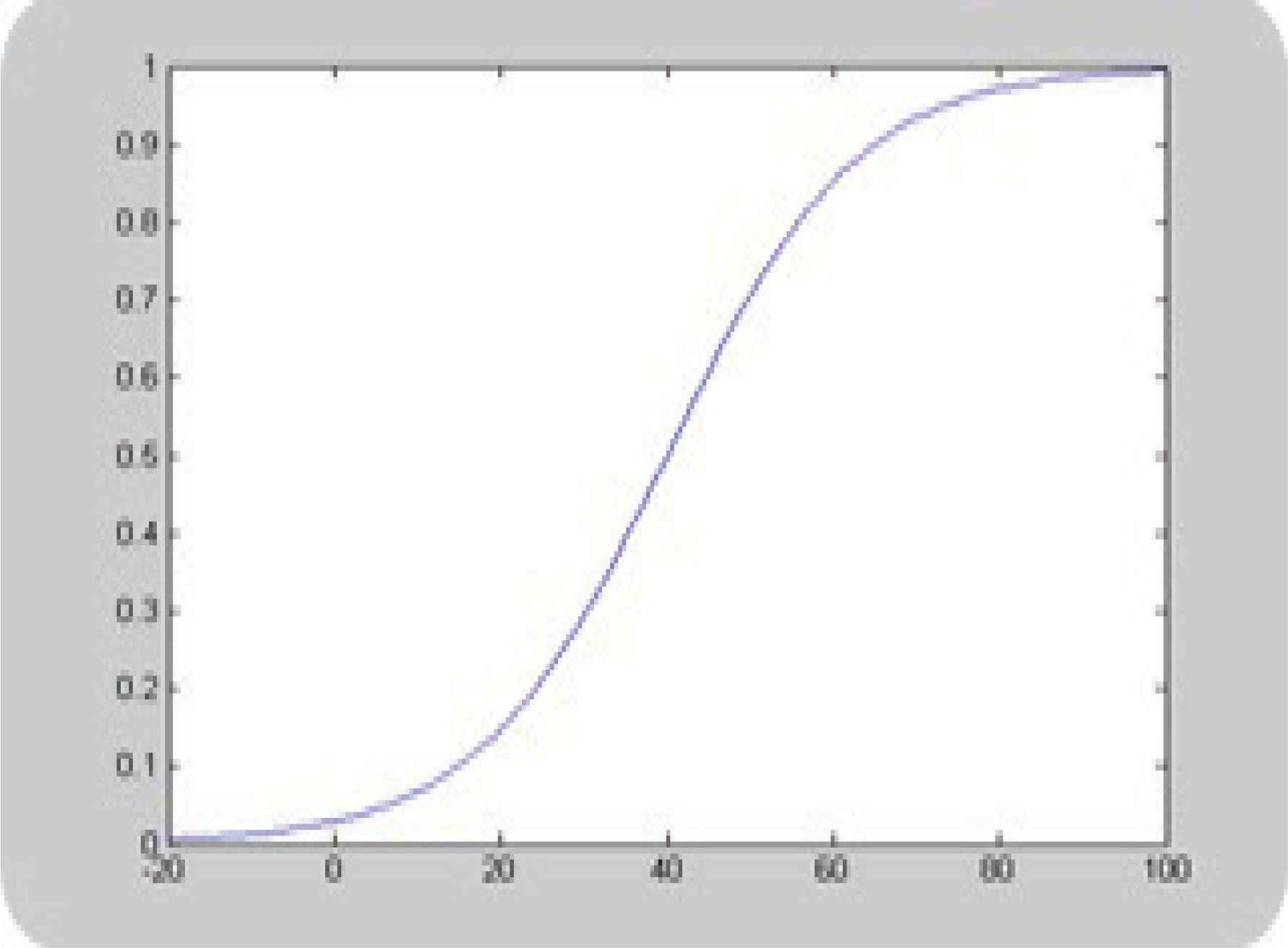
Columns 2 and 3 of table 4 represent the values of the reciprocal of the hypothesis 1 for gamma and beta variables, called hypothesis 1’, see formula 15, for every variable in the first column.

Gamma Beta Gamma Beta
Inflation 11 5 10.30 5.30
GIP 2 0 2.7007 0.13
Money 7 12 6.866 12.1
Value Future 11 5 6.391 6.35
Inflation Future 2 0 2 0
GIP Future 7 12 7 12
Money Value Time 2 4 1.199 4.14
Table 4.

Optimization of 1’ results.

After the optimization of the set of parameters of the membership functions and by using an actual database and based on the predicates obtained from the hypothesis 1’ about the Mexican economy, the results of gamma and beta changed to those resumed in columns 4 and 5.

Table 5 resumes the values of the membership functions for gamma and beta obtained from hypotheses 1, 2 and 3 and 1′, 2′ and 3′. The primes indicate that the hypothesis is substituted by its corresponding reciprocal. We took into account the possible states of the variables and we used sigmoidal membership functions, negation of the sigmoidal and Gaussian.

Hypothesis 1 Hypothesis 2 Hypothesis 3 Hypothesis 1′ Hypothesis 2′ Hypothesis 3′
0.13 0.79 0.16 0.90 0.79 0.25
0.04 0.05 0.23 1 0.99 0.19
0.97 0.97 0.97 1.00 0.03 0.26
0.32 0.61 0.51 1.00 0.44 0.29
0.10 0.66 0.59 1.00 0.64 0.55
0.22 0.55 0.72 1.00 0.51 0.65
… … … … … …
0.97 0.97 0.98 1.00 0.06 0.54
0.32 0.56 0.76 1.00 0.45 0.64
0.04 0.82 0.31 1.00 0.82 0.29
0.04 0.72 0.56 1.00 0.72 0.55
0.97 0.97 0.99 1.00 0.16 0.64
0.03 0.73 0.56 1.00 0.74 0.55
0.04 0.59 0.66 1.00 0.64 0.65
0.03 0.60 0.66 1.00 0.64 0.65
0.15 0.49 0.48 1.00 0.36 0.35
0.06 0.73 0.59 1.00 0.55 0.53

The cells in the two final rows represent the truth value of the universal propositions of each hypothesis, for the 15 first years, and the 6 last years, respectively after optimization of 1′

Hypothesis 1′ was the best for original parameters; after optimization, with the new parameters the result was very close to 1.

Example 3.

(Diabetes sickness illustrating the second kind of knowledge discovery), see Ref. 26:

A large Data Base with the following 7 variables, which describe patients, was used to discover knowledge according Diabetes sickness:

  • •

    Age

  • •

    Race

  • •

    Hypertension

  • •

    Body Mass Index (BMI)

  • •

    Cardiovascular and/or Cerebral Vascular Accident (CVA) antecedents (both known for the expression: “Antecedents”).

  • •

    Sex

  • •

    Classification of diabetes (Diabetes).

Combination of Geometric Mean Based Compensatory Logic with the correspondent QL implication was used. Searching in the predicates space for high values of the correspondent universal proposition over the data base set, we obtained the following predicates, with the correspondent truth values of the universal proposition:

    General Predicates

  • (((Race=white) and ((Antecedents=true) and (Age=advanced)))) → ((Classification =diabetes) or (Mass=high)))

    Truth value: 0.9256

  • ((Race=white) or ((((Antecedents=true) and (Age=advanced)) and (Hypertension=true))) → (((Classifications=diabetes) or (Mass=high))) → (Sex=male))))

    Truth value: 0.9205

  • ((Antecedents=true)) → ((((Hypertension=true) and (Mass=high)) and (Age=advanced)) or (Race=white)))

    Truth value: 0.8603

  • ((Antecedents=true)) → (Age=advanced))

    Truth value: 0.8200

  • ((Classification=diabetes)) → ((Antecedents=true)) → (Hypertension =true)))

    Truth value: 0.8131

  • ((Mass=high) or ((Hypertension=true) or (Sex=male)))

    Truth value: 0.8124

    Association Rules

  • (((Classification=diabetes) and (Antecedents=true)))→(Sex=male) )

    True value: 0.9532

  • ((((Race=white) and (Classification=diabetes)) and (Age=advanced)) ) → (Mass=high))

    True value: 0.9189

  • (((Antecedents=true) and (Age=advanced)) ) → (Race=white) and (Sex=male)) or ((Mass=high) or (Hypertension=true))))

    True value: 0.9166

  • ((Antecedents=true) ) → ((Race=white) or (Age=advanced)))

    True value: 0.9125

  • (Age=advanced)) ) → (Hypertension=true)

    True value: 0.9036

  • (((Age=advanced) and (Classification=diabetes)) ) → (((Hypertension=true) and (Mass=high)) and (Race=white)))

    True value: 0.8320

    Classification Rules

  • (((((Sex=male) and (Race=white)) and (Hypertension=true)) and (Age=advanced))) → (Classification=diabetes))

    True value: 0.9741

  • (((Antecedents=true) and ((Mass=high) and (Hypertension=true)))) → (Classification=diabetes))

    True value: 0.9014

  • ((((Age=advanced) and (Antecedents=true)) and (((Hypertension =true) and (Sex=male)) and (Race=white)))) → (Classification=diabetes))

    True value: 0.8907

  • ((((Mass=high) and ((Antecedents=true) and (Hypertension =true))) and (Age=advanced))) → (Classification=diabetes))

    True value: 0.8713

  • (((Antecedents=true) and (Age=advanced)) ) → (Classification=diabetes))

    True value: 0.8347

  • (((Race=white) and ((Sex=male) and (Age=advanced)))) → (Classification=diabetes))

    True value: 0.7173

This example needs to define new concepts, see definitions 4 and 5.

Definition 4.

α1, α2,…,αn-1 ├ φ is a right deductive structure of Bivalent Logic if the formula α1∧α2∧…∧αn-1→φ is valid in the prepositional calculus of the bivalent logic. α1, α2,…,αn-1 are the hypotheses and ├ is the symbol of inference.

For example:

  • ¬Q, P→Q├¬P (Modus Tollens)

  • ¬(P∧ Q) ├¬ P ∨¬ Q (D’ Morgan)

  • P ├ ¬ (¬P) (Double negation)

  • P ∨ Q, ¬P ├ Q (Disjunctive syllogism)

  • P ├ P ∨ Q (Disjunction)

  • P, Q ├ P ∧ Q (Conjunction)

Definition 5.

α1, α2,…,αn-1 ├ φ is a right deductive structure according a CIS, if the formula α1∧α2∧…∧αn-1→φ is valid according CFL where the implication is the correspondent to the predetermined CIS.

Corollary 1.

α1, α2,…,αn-1 ├ φ is a right structure according bivalent logic if and only if α1,α2,…,αn-1 ├ φ is a right deductive structure according the predetermined CIS.

The interpretation of this corollary is: If the premises of any right deductive structure of Bivalent Logic (which are all of them approximately true in the framework of the CIS), we will obtain a thesis approximately true according CFL.

This is not only a notion of interpretability of CFL according to bivalent logic, it is an actual approximate reasoning, because it uses the classical methods of proofs theory of the bivalent logic.

Let us continue with the example by means of a Sequential Demonstration. Predicates with high truth values associated were included in the demonstration as premises.

  1. 1.

    (Age=advanced)) (hypothesis)

  2. 2.

    ¬ (Classification =diabetes)) (hypothesis)

  3. 3.

    (((Race=white) ∧ (Age=advanced)) → (Classification=diabetes)) (premise) True value: 0.7034

  4. 4.

    (((Antecedents=true) ∧ (Age=advanced)) → (Classification=diabetes)) (premise) True value: 0.8347

  5. 5.

    ¬ (Race=white ∧ Age=advanced) Modus Tollens (2,3)

  6. 6.

    ¬ (Antecedents=true ∧ Age=advanced) ModusTollens (2,4)

  7. 7.

    ¬ (Race=white) ∨ ¬ (Age=advanced) D’ Morgan (5)

  8. 8.

    ¬ (Antecedents=true) ∨ ¬ (Age=advanced) D’ Morgan (6)

  9. 9.

    ¬(¬(Age=advanced))) Double negation (1)

  10. 10.

    ¬ (Race=white) Disjunctive Syllogism (7,9)

  11. 11.

    ¬ (Antecedents=true) Disjunctive Syllogism (8,9)

  12. 12.

    ¬ (Race=white) ∨ ¬ (Antecedents=true) Addition (10)

  13. 13.

    ¬ (Race=white) ∧ ¬ (Antecedents=true) Product (10, 11)

Hence, the deductive structures demonstrated were the following:

  • •

    (Age=advanced), ¬(Classification =diabetes) ├ ¬ (Race=white)

  • •

    (Age=advanced), ¬(Classification =diabetes) ├ ¬ (Antecedents=true)

  • •

    (Age=advanced), ¬(Classification =diabetes) ├ ¬ (Race=white) ∨ ¬ (Antecedents=true)

  • •

    (Age=advanced), ¬(Classification =diabetes) ├ ¬ (Race=white) ∧ ¬ (Antecedents=true

The correspondent formulas obtained were the following:

  • •

    (Age=advanced) ∧ ¬(Classification =diabetes) → ¬ (Race=white)

  • •

    (Age=advanced) ∧ ¬(Classification =diabetes) → ¬ (Antecedents=true)

  • •

    (Age=advanced) ∧ ¬(Classification =diabetes) → ¬ (Race=white) ∨ ¬ (Antecedents=true)

  • •

    (Age=advanced) ∧ ¬ (Classification =diabetes)) → ¬ (Race=white) ∧ ¬ (Antecedents=true)

The correspondent truth-values of the obtained formulas calculated using the data was:

  • •

    (Age=advanced) and ¬(Classification =diabetes)) → ¬ (Race=white)

    Truth-value of the universal proposition: 0.6479

  • •

    (Age=advanced) and ¬(Classification =diabetes)) → ¬ (Antecedents=true)

    Truth-value of the universal proposition: 0.8348

  • •

    (Age=advanced) and ¬(Classification =diabetes)) → ¬ (Race=white) ∨ ¬ (Antecedents=true))

    Truth-value of the universal proposition: 0.7419

  • •

    (Age=advanced) and ¬(Classification =diabetes)) → ¬ (Race=white) ∧¬ (Antecedents=true)

    Truth-value of the universal proposition: 0.66021

This example demonstrates that even though we used bivalent methods for deduction, the truth values of the deducted formulas were large, because the premises where large, according to theorem 1.

This illustrates that taking into account theorem 1, bivalent reasoning can be used as heuristic to get new large truth value predicates, from the previous obtained predicates with large truth values.

5. Application of CFL to different areas and an elaboration of computational tools

CFL has been applied to many fields; see point 3 of the conditions of interpretability. These are the following, Ref. 28–49:

  • •

    SWOT-OA

  • •

    Fuzzy Solution for n-person Cooperative Games as a model for Negotiation

  • •

    Competitiveness (BIOMUNDI)

  • •

    Manager Competences and relation with an MBA program

  • •

    Integral Evaluation of Projects.

  • •

    Local Sustainable Development Indexes.

  • •

    SDI Readiness.

  • •

    Data Quality Control (Opportunity, by the development of a new extension principle).

  • •

    Business Process Discovery and Simulation.

  • •

    Learning Evaluation.

  • •

    Model for Selection of target control in Customs.

  • •

    Treatment of Images of Magnetic Nuclear Resonance for discovery of brains substances using genetic algorithms as searching method.

  • •

    Sustainability Report Introduction Readiness.

  • •

    Compensatory Morphology operators.

  • •

    Signals Treatment.

  • •

    Particular problems of Knowledge Discovery including compound problems.

Besides, the software called ICPro and its graphical version called Fuzzy Tree Studio form computational tools for the graphical modeling and calculus with predicates by using CFL and others fuzzy logic systems. They use productively the interpretability properties for semantic modelling; see Fig. 11 and 12.

Fig. 11.

Fuzzy tree studio visual screen.

Fig. 12.

Fuzzy tree studio screen showing computing truth values in a model.

The list of some CFL developed tools is given below; see point 2 of the conditions:

  • •

    BIAS (DSS in organizations using SWOT-OA Analysis).

  • •

    ICPRO (Fuzzy Logic Predicates evaluation and Neural Networks).

  • •

    Fuzzy Tree Studio (New version of ICPRO), see Fig. 12.

  • •

    Visual Prolog program for Knowledge Discovery by CFL and heuristic searching (Open structure).

  • •

    Java Program for Knowledge Discovery by CFL and heuristic searching (Vectorial representation).

  • •

    Different Tools using Pentaho, R, and Weka for BSC and Knowledge Discovery.

  • •

    CFL Ontologies and Compensatory Fuzzy Description Logics (Fuzzy Tree Studio interacting with semantic frameworks including reasoning).

6. Concluding Remarks

In this paper, we have introduced a new definition of interpretable logical theory. Interpretability of a logical theory according language, should be an interpretability according logical theories and paradigms associated with social practices very much in relation with natural and professional language like Logics, Decision Making theories and methods, Mathematical Statistics and others.

We have identified the following steps for demonstrating that a logical theory is interpretable:

  1. 1.

    Creating a new theoretical approach interpretable by Bivalent Logic, and compatible with selected elements of Decision Making theories and Statistics

  2. 2.

    Elaboration of computational tools

  3. 3.

    Applications to different fields

  4. 4.

    Elaboration and application of experiments testing the following elements:

    • 4.1

      Compatibility with human behavior,

    • 4.2

      Compatibility with Knowledge Discovery methods for particular problems

    • 4.3

      Compatibility with Mamdani approach in simple cases,

    • 4.4

      Performance of different deductive structures as heuristics in knowledge discovery as a way of approximate reasoning.

    • 4.5

      Accuracy improvement in complex and high dimensional cases of Fuzzy Control,

    • 4.6

      Compatibility with protoforms used in CWW and LDS

    • 4.7

      Robustness.

An interpretable theory is a feasible approach to reach a transdiciplinary theory.

Compensatory Fuzzy Logic is a paradigm of an interpretable logical theory. For this, we demonstrated, illustrating with some examples that it satisfies points 1, 2 and 3 above.

We propose the following task for demonstrating interpretability:

  1. 1.

    Evaluating how convenient is an alternative according a predicate, obtained from expressions of the DM preferences.

  2. 2.

    Searching new convenient alternatives using that predicate.

  3. 3.

    Evaluating how truth is an expression using facts and/or expert opinions.

  4. 4.

    Estimating how truth is an expression using facts associated to a probabilistic sample.

  5. 5.

    Discovering new knowledge expressed in natural language using heuristic and/or optimization.

  6. 6.

    Demonstrating and discovering new knowledge by reasoning.

Tables 6 and 7 highlight the comparison of CFL with the principal fuzzy ways to use productively the natural language by Fuzzy Logic (Mamdani Fuzzy Inference Systems (MFIS), Integration of membership functions by operators (IMFO) and Computing by words (CWW) and Linguistic Data Summarization (LDS), according to the six tasks elaborated on in the previous discussion.

Theory/Task 1 2 3
CFL By predicates as a function evaluating convenience Searching by increasing truth values of a predicate By the evaluation of the correspondent predicate
MFIS By rules, including convenience like a control variable Not possible naturally Not possible naturally
IMFO By aggregation using operators (including the case of linguistic information by labels) Searching the best according the integration of the information By aggregation of the linguistic information, but it is not obtained a truth, but a membership value or a label
CWW and LDS By specific protoforms Searching by increasing truth values of specific protoforms By the evaluation of specific protoforms
Table 6

Skill comparison by tasks realized with the principal fuzzy ways to use productively the natural language Logic.

Theory/Task 4 5 6
CFL Calculating the truth value of the universal proposition over the sample Possible to get any kind of knowledge by predicates It is possible to discover knowledge, independently of its logic structure and reasoning by any deductive structure of the bivalent logic
MFIS Not possible Possible to get a set of rules in a form of fuzzy inference system Possible to discover knowledge expressed as a set of rules improving the performance of the fuzzy inference system
IMFO Not possible Not possible Not possible
CWW and LDS Not possible Possible to get knowledge correspondent to specific proforms Possible by specific ways associated to the specific proforms
Table 7

Skill comparison by tasks with the principal fuzzy ways to use productively the natural language Logic

7. Recommendations and future works

The current research is very complex because it needs of a big amount of justification for proving interpretability of Compensatory Fuzzy Logic. However, in this paper we have demonstrated an important quantity of these properties.

Future researches and papers should include some aspect not treated in this paper; particularly the objectives explained in points 4, which are enumerated above:

  1. 4.

    Elaboration and application of experiments testing the following elements:

    • 4.1

      Compatibility with human behavior,

    • 4.2

      Compatibility with Knowledge Discovery methods for particular problems

    • 4.3

      Compatibility with Mamdani approach in simple cases,

    • 4.4

      Performance of different deductive structures as heuristics in knowledge discovery as a way of approximate reasoning.

    • 4.5

      Accuracy improvement in complex and high dimensional cases of Fuzzy Control,

    • 4.6

      Compatibility with protoforms used in CWW and LDS

    • 4.7

      Robustness.

References

1.RA Espín - Andrade, AC Bataller, J Marx-Gomez, and A Racet, Fuzzy Semantic Transdisciplinary Knowledge Discovery Approach for Business Intelligence, Towards a Transdisciplinarian Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making, Shaker Verlag, 2011, pp. 13-34. http://dx.doi.org/10.5220/0006053601990207
2.K Passino and C Yurkovich, Fuzzy Control, Addison Wesley, Menlo Park, 1998. http://dx.doi.org/10.1080/03081070008960938
3.R Yager and D Filev, Essentials of Fuzzy Modeling and Control, John Wiley and sons, New York, 1994. http://dx.doi.org/10.1145/222267.1065840
4.F Herrera and E Herrera-Viedma, Linguistic decision analysis: steps for solving decision problems under linguistic information, Fuzzy Sets and Systems, Vol. 115, 2000, pp. 67-82. http://dx.doi.org/10.1016/s0165-0114(99)00024-x
5.RM Rodríguez and L Martínez, “An Analysis of Symbolic Linguistic. Computing Models in Decision Making”, International Journal of General Systems, Taylor and Francis, Vol. 42, No. 1, 2013, pp. 121-136. http://dx.doi.org/10.1080/03081079.2012.710442
6.L Martínez and F Herrera, “An overview on the 2-tuple linguistic model for Computing with Words in Decision Making: Extensions, applications and challenges”, Information Sciences, Elsevier, Vol. 207, No. 1, 2012, pp. 1-18. http://dx.doi.org/10.1016/j.ins.2012.04.025
7.D Dubois, F Esteva, L Godo, and H Prade, Fuzzy-Set Based Logics. A history oriented presentation of their main development, The Many Valued and Non-monotonic Turn Logic, Handbook of the History of Logic, Elsevier, 2007, pp. 325-449. http://dx.doi.org/10.1016/s1874-5857(07)80009-4
8.F Herrera and E Herrera-Viedma, Study of the Origin and Uses of the Ordered Weighted Geometric Operator in Multicriteria Decision Making, International Journal of Intelligent Systems, Vol. 18, 2003, pp. 689-707.
9.P Hájek, Metamathematics of Fuzzy Logic, Kluwer, 1998. http://dx.doi.org/10.1007/978-94-011-5300-3
10.P Hájek, Comments on Interpretability and Decidability in Fuzzy Logic, J. Logic Computation, Vol. 21, No. 5, 2011, pp. 823-828. http://dx.doi.org/10.1093/logcom/exp058
11.S Guillaume, Designing Fuzzy Inference Systems from Data: An Interpretability-Oriented Review, IEEE Transactions on Fuzzy Systems, Vol. 9, No. 3, 2001, pp. 426-443. http://dx.doi.org/10.1109/91.928739
12.JM Alonso and L Magdalena, An Experimental Study on the Interpretability of Fuzzy Systems, in proc. IFSA/EUSFLAT Conf. (2009), pp. 125-130. eds. http://dx.doi.org/10.1016/j.ijar.2009.09.004
13.MJ Gacto, R Alcalá, and F Herrera, Interpretability of linguistic fuzzy rule-based systems: An overview of interpretability measures, Information Sciences, Vol. 181, No. 20, 2011, pp. 4340-4360. http://dx.doi.org/10.1016/j.ins.2011.02.021
14.W Pedrycz and A Vasilakos, Linguistic models and linguistic modeling, IEEE Trans. on Systems, Man and Cybernetics, Vol. 29, 1999, pp. 745-757. http://dx.doi.org/10.1109/3477.809029
15.LA Zadeh, Precisiated natural language (PNL), AI Mag, Vol. 25, No. 3, 2004, pp. 74-91. http://dx.doi.org/10.1109/fuzzy.2004.1375673
16.LA Zadeh, A prototype-centered approach to adding deduction capability to search engines-the concept of protoform, in proc. Fuzzy Information Processing Society, 2002. Proceedings. NAFIPS. 2002 Annual Meeting of the North American (2002), pp. 523-525. eds. http://dx.doi.org/10.1109/nafips.2002.1018115
17.J Kacprzyk and S Zadrozny, Linguistic database summaries and their proforms: towards natural language based knowledge discovery tools, Information Sciences, Vol. 173, 2005, pp. 281-304. http://dx.doi.org/10.1016/j.ins.2005.03.002
18.J Kacprzyk and S Zadrozny, Computing with words is an implementable paradigm: Fuzzy Queries, Linguistic Data Summaries and Natural Language, IEEE Transactions on Fuzzy Systems, Vol. 18, No. 3, 2010, pp. 461-472. http://dx.doi.org/10.1109/tfuzz.2010.2040480
19.B Poizat, A course in model theory: an introduction to contemporary mathematical logic, Springer Science & Business Media., 2012. http://dx.doi.org/10.2307/3620549
20.A Tarski, A Mostowski, and RM Robinson (editors), Undecidable theories, Elsevier, 1953. http://dx.doi.org/10.2307/3611179
21.RA Espín-Andrade, E Fernández, and E González, A logic system for reasoning and decision making: Compensatory Fuzzy Logic on Geometric Mean (in spanish), Revista Investigación Operacional, Vol. 32, 2012, pp. 230-245. http://dx.doi.org/10.1007/978-3-642-53737-0_2
22.RA Espín-Andrade, E Fernández, and E González, Compensatory Fuzzy Logic: A Frame for Reasoning and Modeling Preference Knowledge in Intelligent Systems, Soft Computing for Business Intelligence, Springer, Berlin Heidelberg, 2014, pp. 3-23. http://dx.doi.org/10.1007/978-3-642-53737-0_1
23.A Bouchet, Arithmetic Mean Based Compensatory Fuzzy Logic, International Journal of Computational Intelligence and Applications, Vol. 10, No. 2, 2011, pp. 231-243. http://dx.doi.org/10.1142/s1469026811003070
24.TL Saaty, Decision making-the analytic hierarchy and network processes (AHP/ANP), Journal of systems science and systems engineering, Vol. 13, No. 1, 2004, pp. 1-35. http://dx.doi.org/10.1007/s11518-006-0151-5
25.TL Saaty, Time dependent decision-making; dynamic priorities in the AHP/ANP: Generalizing from points to functions and from real to complex variables, Mathematical and Computer Modelling, Vol. 46, No. 7, 2007, pp. 860-891. http://dx.doi.org/10.1016/j.mcm.2007.03.028
26.A Racet, Compensatory Fuzzy Ontology: A New Solution for Ontology Engineering, Towards a Transdisciplinarian Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making, Shaker Verlag, 2011, pp. 126-140. http://dx.doi.org/10.5220/0005603802450250
27.RA Espín-Andrade, E González, E Fernández, and MM Alonso, Compensatory Fuzzy Logic Inference, Soft Computing for Business Intelligence, Springer, Berlin Heidelberg, 2014, pp. 25-43. http://dx.doi.org/10.1007/978-3-642-53737-0_2
28.RA Espín-Andrade, A Vanti, J Marx, and A Racet, SWOT-OA Fuzzy Analysis for Strategic Plan Evaluation and Decision Making Support, Towards a Transdisciplinary Technology for Business Intelligence, Shaker Verlag, 2011, pp. 89-111. http://dx.doi.org/10.1007/978-3-642-10781-8_5
29.E González, RA Espín-Andrade, and G Mazcorro, Fuzzy Negotiation Solutions of N-Person Cooperative Games by Knowledge Engineering in Bargaining, Group Decision and Negotiation, Vol. 21, No. 2, 2012, pp. 133-152. http://dx.doi.org/10.1007/s10726-011-9244-8
30.I Marrero, Business Intelligence and Competitive Intelligence: Importance of their combined use to Support Organizational Decision Making, Towards a Transdisciplinarian Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making, Shaker Verlag, 2011, pp. 35-47. http://dx.doi.org/10.1201/9781420013900.ch6
31.AMP Fernández, A Vanti, RA Espín-Andrade, A Pérez, and J Marx, Proposta de um Modelo de Medição de Desempenho Logístico Apoiado pela Lógica Difusa: O Caso de umaIndústria de Motores, RISTI - Revista Ibérica de Sistemas e Tecnologias de Informação, Vol. 3, 2009, pp. 53-64. http://dx.doi.org/10.17013/risti.16.92-107
32.A Vanti, RA Espín-Andrade, A Pérez, and D Ciotta, Strategic Themes for Balanced Scorecard Construction Based on fuzzy logic, The International Journal of Applied Management and Technology, Vol. 6, 2008, pp. 4-39. http://dx.doi.org/10.1002/9781119200871.ch2
33.MA Gonzalez, GJ Meschino, RA Espin, and VL Ballarin, Classification of over-segmented regions result of the watershed transform through compensatory fuzzy logic, Towards a Transdisciplinarian Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making, Shaker Verlag, 2011, pp. 161-168. http://dx.doi.org/10.2991/.2013.3
34.A Vanti, Competitive Advantage through costumer relationship: the case of a car part-seller company, E-Business Issues, Challenges and Opportunities for SMEs: driving Competitiveness, Lisboa, 2010, pp. 2. http://dx.doi.org/10.4018/978-1-61692-880-3.ch001
35.A Vanti, Informational analysis for internal auditing involving application of complex information systems, Springer, Bridgeport, in proc. CISSE - IEEE, 2008, Bridgeport. International Conferences on Computer, Information, and Systems Sciences, and Engineering Memories (2008). eds. http://dx.doi.org/10.1007/978-90-481-3660-5_23
36.PM Marín, RA Espin-Andrade, P Pérez, L García, and R Pérez, Fuzzy Method for Balanced Scorecard Design, Towards a Transdisciplinary Technology for Business Intelligence, Shaker Verlag, 2011, pp. 73-88. http://dx.doi.org/10.1007/978-3-540-24700-5_13
37.J Cejas, RA Espín-Andrade, and D Alfonso, Application of Compensatory Fuzzy Logic in company sector (In Spanish), Dyna, Vol. 87, No. 3, 2012, pp. 271-274. http://dx.doi.org/10.2991/.2013.3
38.GJ Meschino, RA Espín-Andrade, and VL Ballarin, A framework for tissue discrimination in Magnetic Resonance brain images based on predicates analysis and Compensatory Fuzzy Logic, International Journal of Intelligent Computing in Medical Sciences & Image Processing, Vol. 2, No. 3, 2008, pp. 207-222. http://dx.doi.org/10.1080/1931308x.2008.10644165
39.GJ Meschino, VL Ballarin, and RA Espin-Andrade, Image Segmentation with Predicates Analysis and Compensatory Fuzzy Logic, Towards a Transdisciplinary Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making, Shaker Verlag, 2011, pp. 210-225. http://dx.doi.org/10.2991/.2013.3
40.A Bouchet, JI Pastore, RA Espin-Andrade, M Brun, and VL Ballarin, Compensatory Logic applied to Digital Image Processing, Towards a Transdisciplinarian Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making, Shaker Verlag, 2011, pp. 226-235. http://dx.doi.org/10.2991/.2013.2
41.D Dechkova and R Miranda, Introduction of Sustainability Report in an Enterprise: Decision Making Model Based on Compensatory Fuzzy Logic, Softcomputing for Business Intelligence, Springer Verlag, 2014, pp. 247-272. http://dx.doi.org/10.1007/978-3-642-53737-0_17
42.GJ Meschino, M Nabte, S Gesualdo, A Monjeau, and LI Passoni, Fuzzy Tree Studio: a tool for the design of the Scorecard for the Management of Protected Areas, Soft Computing for Business Intelligence, Springer, Berlin Heidelberg, 2014, pp. 99-112. http://dx.doi.org/10.1007/978-3-642-53737-0_6
43.A Rosete, T Ceruto, RA Espin, and J Marx-Gomez, A General Method for Knowledge Discovery Approach using Compensatory Logic and metaheuristics, Towards a Transdisciplinarian Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making, Shaker Verlag, 2011, pp. 240-270. http://dx.doi.org/10.2991/.2013.6
44.RA Espin-Andrade, E González, and E Fernández, A fuzzy approach to Prospect Theory, Softcomputing for Business Intelligence, Springer Verlag, 2014, pp. 41-64. http://dx.doi.org/10.1007/978-3-642-53737-0_3
45.M Martínez and RA Espín-Andrade, Knowledge discovery by Compensatory Fuzzy Logic predicates using a metaheuristic approach, Softcomputing for Business Intelligence, Springer Verlag, 2014, pp. 165-178. http://dx.doi.org/10.2991/.2013.3
46.T Ceruto, O Lapeira, A Rosete, and RA Espín, Discovery of fuzzy predicates in database, JC Leyva (editor), Atlantis Press, in proc. Fourth International Workshop on Knowledge Discovery, Knowledge Management and Decision Support (2013). http://dx.doi.org/10.2991/.2013.6
47.M Martínez and RA Espín-Andrade, Knowledge Discovery by Compensatory Fuzzy Logic Predicates using a metaheuristic approach., Studies on Knowledge Discovery, Knowledge Management and Decision Making. Advances in Intelligent Systems Research Series, Atlantis Press, 2013. http://dx.doi.org/10.2991/.2013.3
48.PM Marín, RA Espín-Andrade, and J Marx-Gomez, Multivalued Fuzzy Logic: A sensitiveness analysis, Studies on Knowledge Discovery, Knowledge Management and Decision Making. Advances in Intelligent Systems Research Series, Atlantis Press, 2013. http://dx.doi.org/10.2991/.2013.1
49.A Bouchet, GJ Meschino, M Brun, RA Espín, and V Ballarin, Linguistic Interpretation of Mathematical Morphology, Studies on Knowledge Discovery, Knowledge Management and Decision Making. Advances in Intelligent Systems Research Series, Atlantis Press, 2013. http://dx.doi.org/10.2991/.2013.2
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
International Journal of Computational Intelligence Systems
Volume-Issue
9 - 4
Pages
612 - 626
Publication Date
2016/08/01
ISSN (Online)
1875-6883
ISSN (Print)
1875-6891
DOI
10.1080/18756891.2016.1204111How to use a DOI?
Copyright
© 2016. the authors. Co-published by Atlantis Press and Taylor & Francis
Open Access
This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Rafael A. Espin-Andrade
AU  - Erick Gonzalez
AU  - Witold Pedrycz
AU  - Eduardo Fernandez
PY  - 2016
DA  - 2016/08/01
TI  - An Interpretable Logical Theory: The case of Compensatory Fuzzy Logic
JO  - International Journal of Computational Intelligence Systems
SP  - 612
EP  - 626
VL  - 9
IS  - 4
SN  - 1875-6883
UR  - https://doi.org/10.1080/18756891.2016.1204111
DO  - 10.1080/18756891.2016.1204111
ID  - Espin-Andrade2016
ER  -